多普勒积分时长对星间测速精度影响分析
尚湘安 萧鑫 高杰 张攀 宋宝相
(1 西安空间无线电技术研究所,西安 710071)(2 中国空间技术研究院,北京 100094)
目前世界范围内卫星应用进入了全面产业化阶段,业务领域包括:通信、电视、导航、遥感等,逐渐融入了国民经济的各个领域,给人们的日常生活带来了极大的方便。与此同时,卫星也向着高、中、低多轨道,集群化、星座化和网络化发展,卫星之间的无线链路得到了广泛的应用,如GPS、铱星(Iridium)、“北斗”等卫星内部都建立了星间链路。卫星之间的星间链路可以实现通信和测控的功能,星间速度测量精度是重要指标之一,测量结果用于星间位置确定、时频同步等过程中,对于提高星座的能力、稳定自主运行和安全具有重要的作用[1-2]。
由于卫星处在高速运动的状态之中,星座内两颗卫星之间的距离可能会有较大的变化,体现出较大的速度变化率。为了实现卫星之间的测控功能,星间链路一般具有遥控遥测传递的功能,同时可以进行两星间距离、时差、频差和速度等时频参数测量[3]。国内外星间速度测量大多通过测量接收对方卫星信号载波相位积分多普勒变化率实现,通常测量精度可以达到1 m/s量级。多普勒变化率测量是在一定时间间隔区间上进行测量的结果,反映出所在区间内多普勒频率平均变化率,所以在星间速度存在较大变化率的情况下,不同测量时间间隔会引入不同程度的速度测量误差。过长的积分测量时间间隔会带来较大的星间速度测量误差,导致指标超差,不能满足系统使用要求。
本文首先通过具体双星星座轨道特性研究,获得两颗卫星之间的相对运动速度变化规律。然后,介绍星间测速功能实现的原理。最后,研究建立不同多普勒变化率积分区间时长情况下的星间速度测量误差数学关系,通过Matlab软件编程进行仿真计算。
1 双星星座轨道特性
双星星座结构简单,通过星间链路进行测控信息传递和时间同步,可以扩大卫星对地观测范围,提高遥感测量精度,提高卫星装载载荷的能力、数量和种类,得到了广泛的应用。双星星座中的两颗卫星根据不同的构型需求可以设计成不同的轨道类型:同轨道面或不同轨道面。当两颗星处于同一个轨道面时,一颗卫星在前,另一颗卫星在后,两颗卫星之间的距离变化不大,相对速度较小,速度测量容易实现。当两颗卫星不在同一个轨道面时,两颗卫星存在相对运动,相对距离和速度都处于动态变化过程中[4]。异轨道面星间链路速度测量受到两星间动态效应影响,对测量的时效性要求较高,是本文的研究重点。下面通过典型的异轨道面星间链路轨道参数仿真研究,得到两颗星之间的相对运动关系,作为后续测速误差分析的依据。
对于卫星来说,在地球引力的作用下,其轨道运行可看作二体问题。卫星所受的其他力,如大气阻力、日月引力、辐射压力等都会使卫星偏离理想轨道,因此,卫星轨道参数的求解需要考虑多种因素影响和通过复杂的数学计算实现。根据圆轨道卫星在地球惯性坐标系中的轨迹方程,通过对轨道动力学和球面三角形的几何分析,可以写出卫星在天球球面上对应点的轨迹方程为[5]
(1)
式中:φ为矢径与赤道平面夹角;λ为子午线向东到矢径在赤道面投影的角距;i为卫星轨道面倾角;t为时间,从卫星经过升交点位置开始算起;Ω0为升交点位置;γ为卫星的初始相位;ω为卫星绕地球旋转的角速度;ωe为地球自转的角速度。根据球面上任意两点间距离公式和余弦定理及式(1),可得到卫星a与卫星b间的星间链路(ISL)距离的时间导数(速度)计算公式为
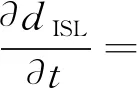
cos (γb+ωt)+sini·sinφb·cos (γa+ωt)]}ω×{(cos2(Δ/2)-cos2i·sin2(Δ/2)cos (γa-γb)+cosi·sinΔ·sin (γa-γb)-sin2i×sin2(Δ/2) sin(γa+γb-2ωt)}
(2)
式中:dISL为星间距离,γa和γb分别为卫星a、b的初始化相位;H和Re分别为轨道高度和地球半径;Δ为轨道面间夹角;φa和φb分别为卫星a、b的近地点俯角。
在两颗卫星初始相位γa≈γb=γ,且轨道面夹角Δ很小时,式(2)可以简化为
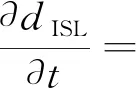
(3)
即,
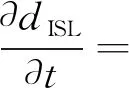
(4)
设
A=(H+Re)·ω·[sin2(Δ/2)·
sini(sinφa+sini·sinφb)]
(5)
则
(6)
由(6)式可以看出,两颗卫星之间的速度变化规律可近似为余弦函数关系。
本文使用STK卫星仿真工具包进行卫星星座仿真,得到仿真计算结果如下。
首先在STK软件中设置仿真开始和结束时间,输入构成星座的两颗卫星的基于地心赤道坐标系的平根轨道参数[6],见表1。

表1 卫星的轨道参数Table 1 Orbital parameters of the satellites
通过运行软件进行双星在轨特性仿真,得到星座在空间的3D效果如图1所示。
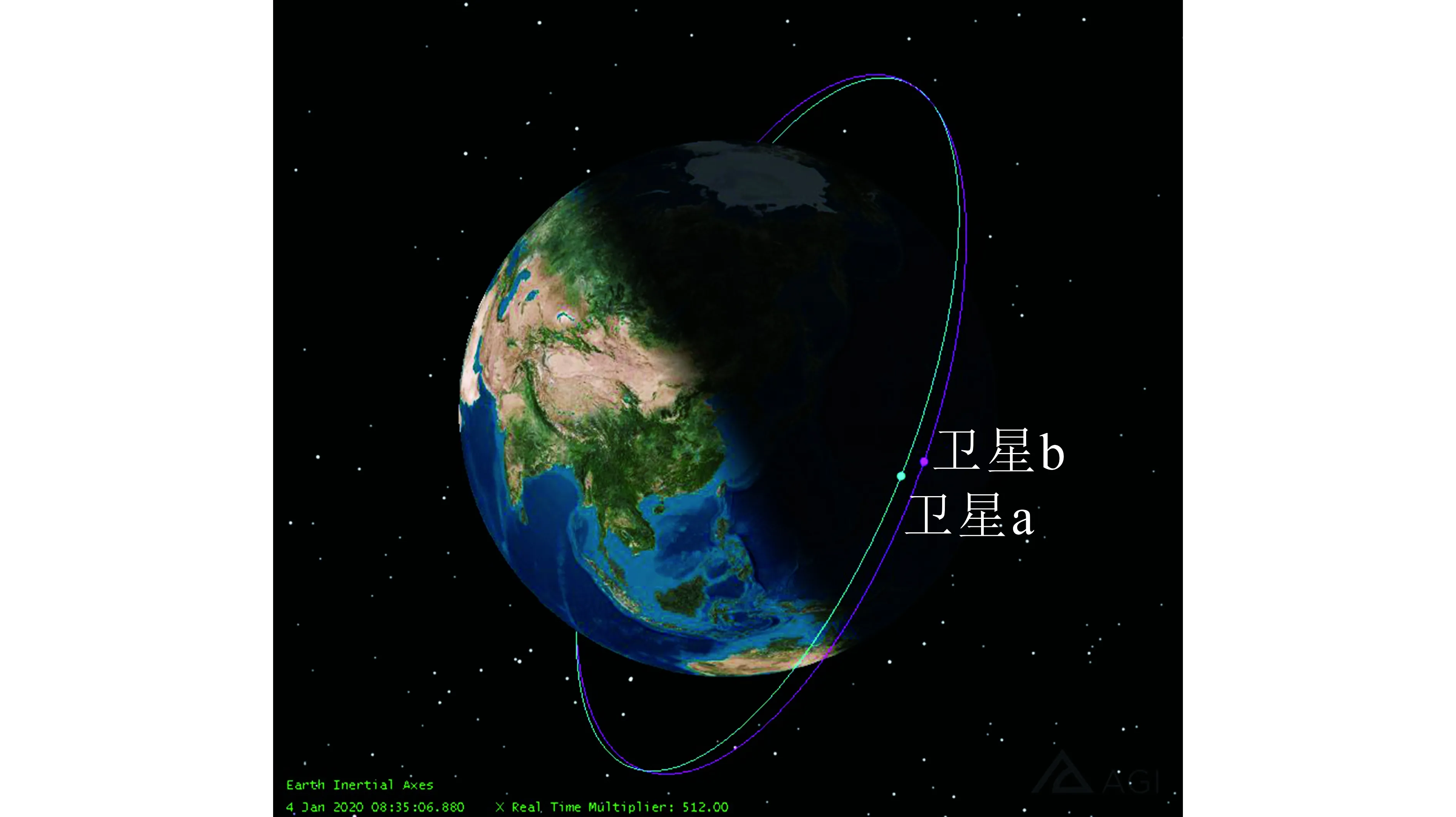
图1 双星星座效果图Fig.1 Effect of two satellites
在软件中,通过报告和图表功能查看两颗卫星之间的接近速度参数,并绘制两星间相对速度变化规律曲线如图2所示,星座运行周期见表2。
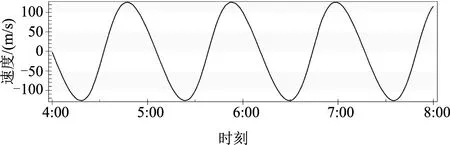
图2 双星间相对运动速度仿真曲线Fig.2 Simulation curve of two satellite relative velocity
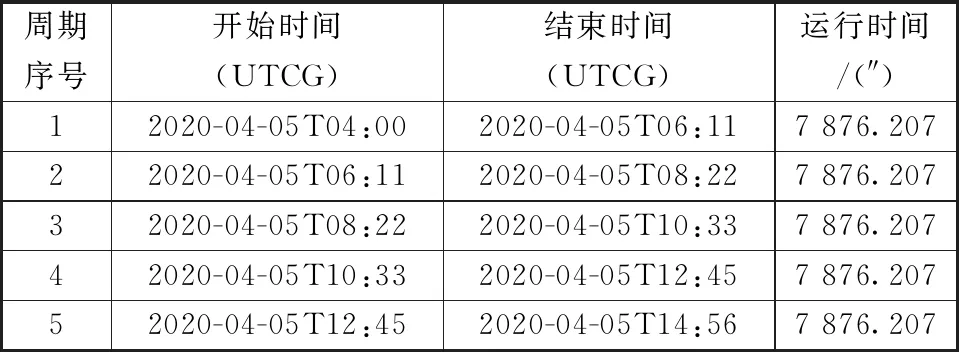
表2 双星绕地球运行周期Table 2 Operating period of the two satellites circling the earth
由图2和表2可知:两颗卫星间的速度变化范围是[-130 m/s,+130 m/s];星间速度和加速度参数变化的周期与星座绕地球运行周期一致,都是约为7876 s。
2 星间测速功能实现方法
星间测速可以通过星地测控链路、导航星或星间链路进行时频测试实现。星地测控由于可见弧段时间限制和大气等因素影响测速精度不高,双星通过星间链路收发信号,进行双向时间比对获得伪距、伪距变化率,计算获得星间速度数据,是一种实现简单、测量精度高、设备可靠性高的方案,星间双向比对实现原理如图3所示。
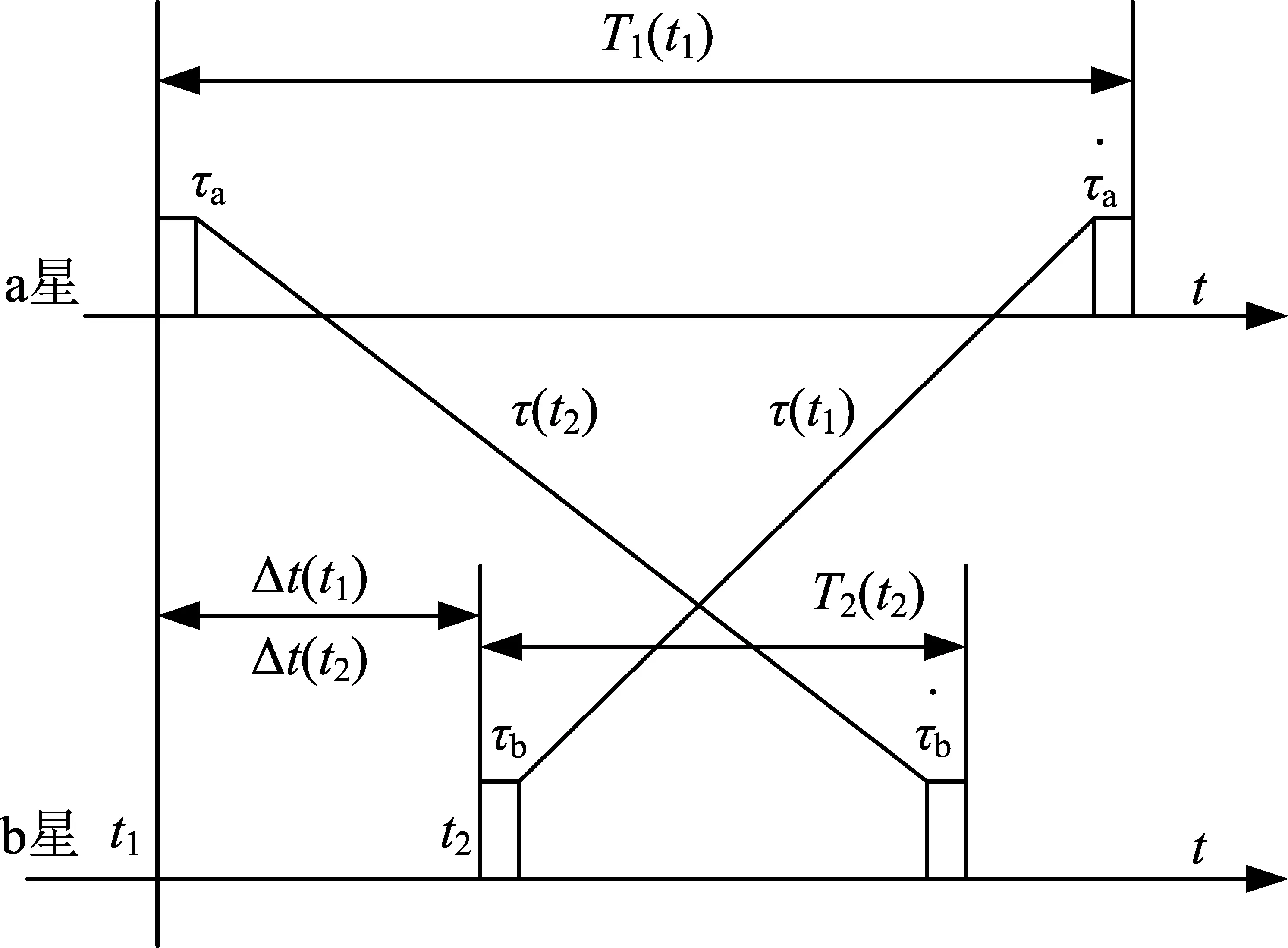
图3 星间双向比对测试原理图Fig.3 Principle of two way time transfer measurement
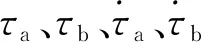
两星各自独立地以本地测量信息和对方发来的测量信息分别通过自动计算处理得到星间时差、频差、距离和速度测量值。星间速度计算如下[7]
(7)
载波相位测量在一个时间间隔里的变化对应积分多普勒或伪距增量,载波相位测量的变化率给出伪距变化率。多普勒频率的测量和提取通过中频数字锁相环捕获跟踪对方信号载波实现。
中频数字锁相环的主要组成部分都由数字电路实现,如图4所示[8]。数字鉴相器由数字乘法器和累加器构成,环路滤波器为数字滤波器,数控振荡器(DCO)由外加高频时钟驱动的数字合成器构成,输出频率和相位受环路滤波器控制。
环路锁定以后,DCO的频率与输入信号相等,输入信号的任何慢变化(如多普勒频移),全部反映在环路滤波器输出的控制码中,DCO的频率控制码变化量完全与输入信号频率变化一致。多普勒频率控制字平均法测速过程就是从载波跟踪过程的控制字更新到采样积分时间的平均过程,最后打时标的时刻为积分的终止时刻。
频率控制码的变化量乘以确定的常数等于输入信号的多普勒频移,这样输出频率控制码就完成了多普勒频率的提取和测量,以环路滤波器运算重复周期为间隔连续输出频率控制码,即可连续输出速度值。
设备测速间隔越短,测速精度就高,输出测量结果频次也可以提高。但是随着测速间隔变短,对硬件设备的计算能力、规模和工作时钟需求也提高。所以通常设计时,需在速度测量精度指标和硬件代价方面进行折中考虑。
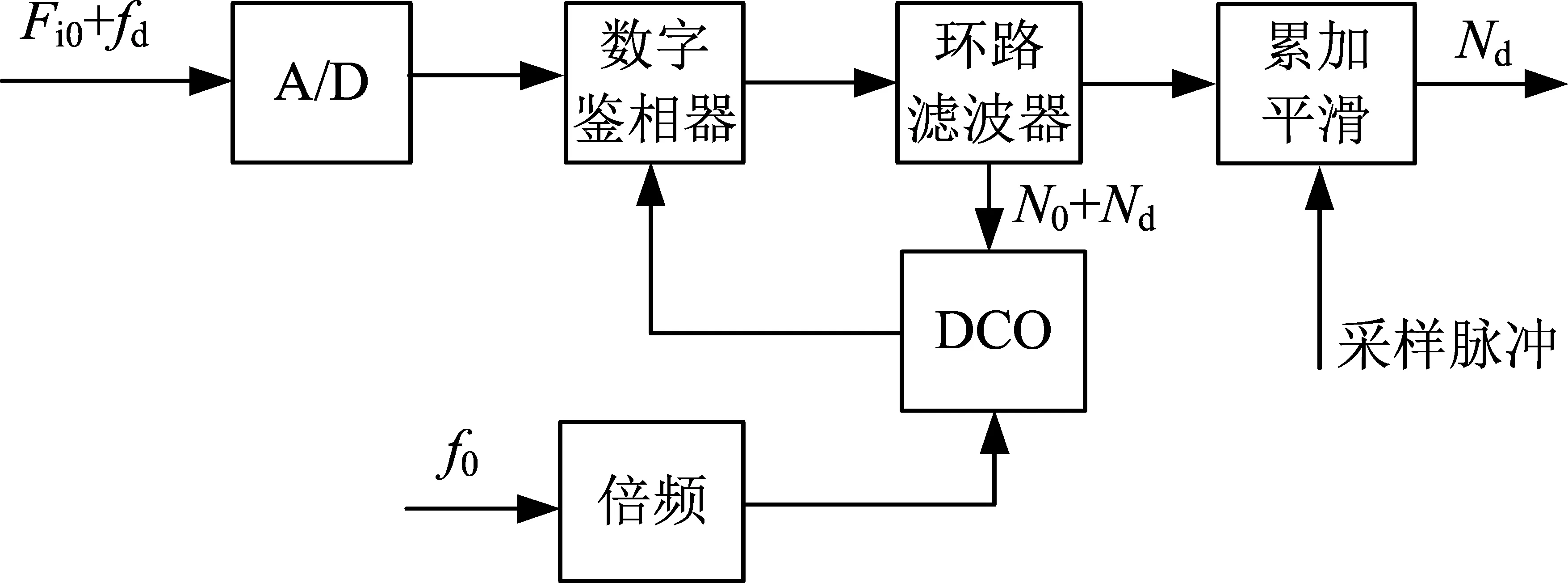
注:Fi0为输入中频频率,fd为多普勒频偏,f0为参考频率,N0为中频频率控制字,Nd为多普勒频率控制字。
3 星间速度测量精度分析
在实际卫星星座内的卫星由于轨道的差异,卫星之间存在着相对运动,卫星之间通过星间链路进行速度测量,需要进行固定时间内的多普勒积分测量,由于在积分时段内卫星的运动速度可能发生变化,从而给速度测量带来一定误差。以下结合前文双星轨道特性分析得出的结论,进行双星间速度测量误差分析。
由第1节得到两颗卫星间的速度变化范围是[-130 m/s,+130 m/s],星间加速度变化范围是[-0.20 m/s2,+0.25 m/s2]。卫星入轨初期,轨道参数误差较大,地面逐步进行变轨控制使卫星进入预定轨道。变轨期间双星间速度和加速度变化较大。为此,卫星总体提出星间速度测量范围为[-150 m/s,+150 m/s],星间加速度适应范围为[-13.5 m/s2,+13.5 m/s2]。
由双星在轨速度变化曲线(见图2)可以看出:星间速度最大时,加速度小;星间速度小时,加速度大。考虑到地面测试验证的便利性,在设备研制过程中,采用正弦规律的曲线近似模拟双星间速度运动情况。以下给出星间速度模拟曲线幅度和周期确定的过程。
星间链路的工作频率设计为10 GHz,由星间速度测量范围[-150 m/s,+150 m/s],可以得到星间载波多普勒频率最大值为5 kHz。由星间多普勒频率最大变化值可以得到星间多普勒频率fv的如下变化规律
fv=5000cos(ωt)
(8)
由式(8)求导,可以得出星间多普勒频率变化率为
(9)
由星间加速度适应范围为[-13.5 m/s2,+13.5 m/s2],可得星间最大多普勒变化率为446.7 Hz/s,所以
5000ω=446.7
(10)
(11)
(12)
(13)
基于以上星间速度运行关系,进行中频数字多普勒积分时间设计。设积分时间为Δt(单位为s),则抽样计算时刻的星间速度(单位为m/s)理论值为
(14)
式中:n为抽样点顺序计数值。
在抽样间隔很小的情况下,近似认为星间速度按线性规律变化,星间链路抽样时刻测得的星间速度为
(15)
由此,得到星间链路速度测量误差为
(16)
将以上关系通过Matlab软件进行编程,通过对不同积分时间长度的速度测量误差进行计算[9],可以得到一组星间速度测量误差曲线,在星间链路设计时作为测速多普勒积分时长选择的依据。
图5给出积分时间为200 ms时的速度误差数值分析结果。可以看出星间速度测量误差在[-1.4 m/s,+1.4 m/s]范围内,误差的最大值位于速度过零点时,因为过零点时两星间的加速度最大。
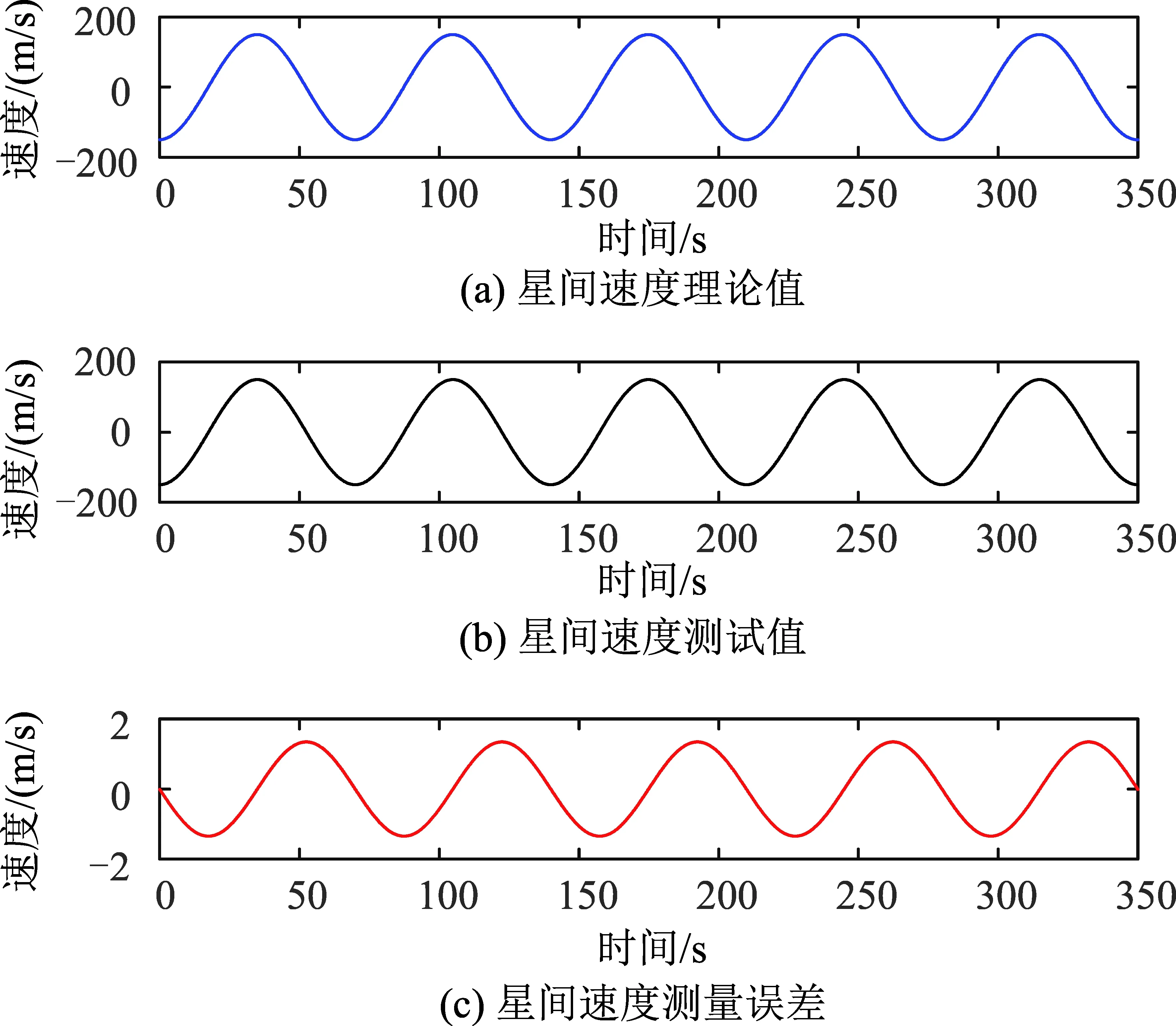
图5 积分时长为200 ms时星间速度计算、测试及测量误差数值分析结果Fig.5 Curves of inter-satellite velocity calculation, test and measurement error when the integral time is 200ms
在多普勒积分时长为200 ms的情况下,通过文献[10]描述的信道模拟器模拟星间动态变化情况对星间链路设备进行了测试验证,测试结果如图6所示。模拟测试结果表明:星间速度测量误差在[-1.4 m/s,+1.4 m/s]之间,星间速度测试误差指标计算结果与模拟测试结果一致。

图6 积分时长为200 ms时星间速度量模拟测试误差曲线Fig.6 Curves of inter-satellite velocity simulation test error when the integral time is 200ms
双星在轨稳定运行期间最大加速度不大于0.25 m/s2。在200 ms积分时段内,速度变化最多为0.25 m/s2×0.2 s=0.05 m/s。200 ms多普勒积分时长可以达到0.025 m/s的星间测速精度,满足实际在轨星间速度测量需要。
通过减小多普勒积分时间,可以减小速度测量误差。将积分时间缩短到20 ms,速度测速误差将减小到[-0.14 m/s,+0.14 m/s]以内,如图7所示。但是积分时间变短,测试结果会受到热噪声、定时脉冲稳定性等其他因素的影响,需要进行折中考虑。
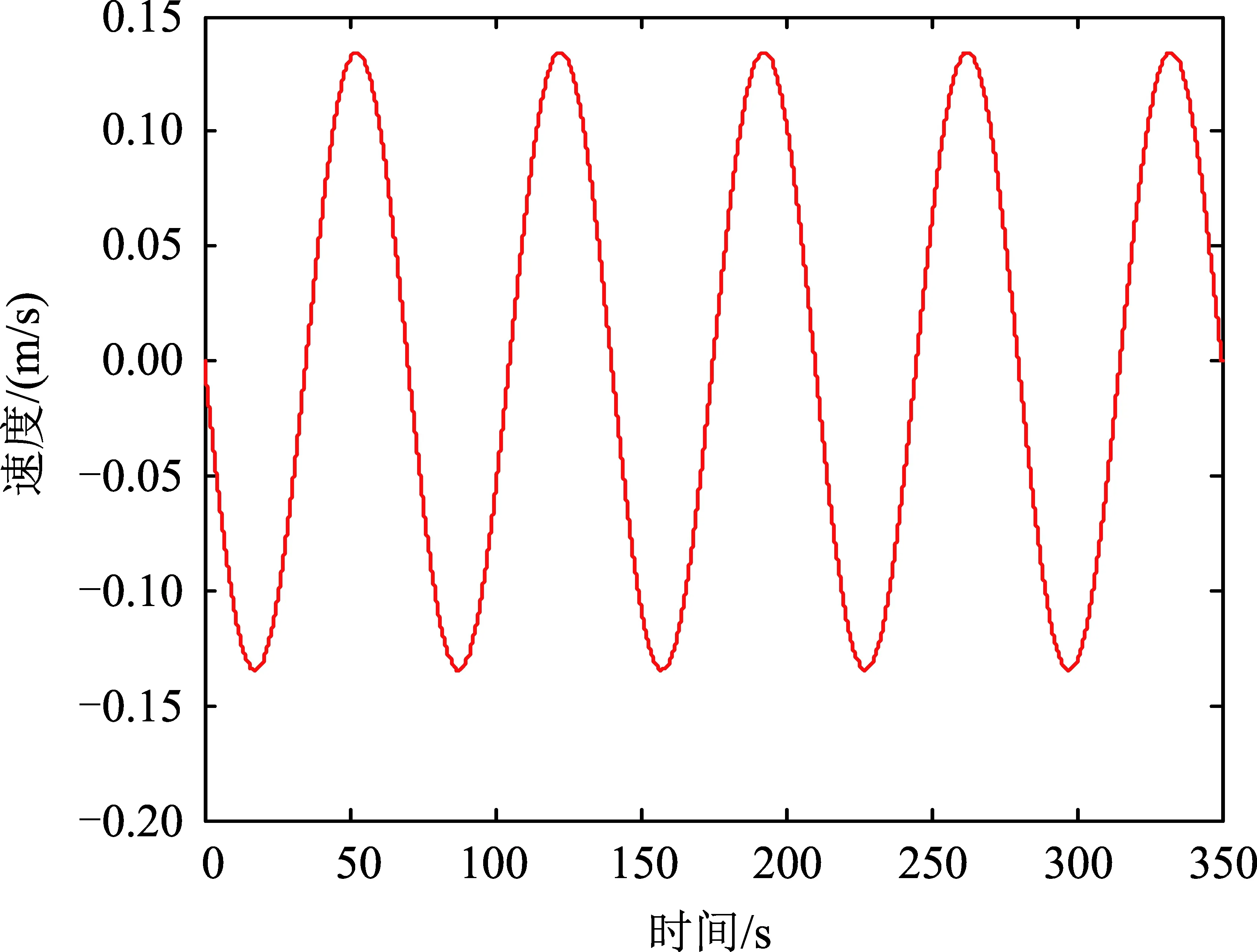
图7 积分时长为20 ms时星间速度测量误差情况仿真曲线Fig.7 Simulation curve of inter-satellite velocity measurement error when the integral time is 20ms
4 结束语
本文得出了多普勒积分时长对星间速度测量精度的影响情况:多普勒积分时间越短,速度测量的实时性和准确性越高。星间测速精度的提高对于卫星星座的自主运行和对地观测精度的提高具有重要的意义,但是随着积分时长的变短,对星间链路的信噪比指标、时频基准的准确性和数据处理平台的能力都提出了较高的要求,需要进行折中考虑。随着新的硬件平台和滤波软件算法的出现,星间测速精度指标会实现更高的测量精度。

