V型电热驱动器理论模型及动态特性

陈 浩, 王新杰, 王 炅, 席占稳, 聂伟荣

(南京理工大学 机械工程学院， 南京 210094)

与静电、压电和电磁等驱动器相比，电热驱动器由于具有输出位移、力大、工艺兼容性好等优点[1-3]，一直是微驱动研究的热点之一.电热驱动器的驱动原理为驱动器通电，由焦耳热效应产生热，然后由热膨胀变形最终产生运动位移.目前，电热驱动器主要分为U型和V型驱动器.相较于U型驱动器，V型电热驱动器的输出力更稳定.因此，构建V型电热驱动器多物理场耦合模型有助于优化设计，进而提高其使用性能.

目前，关于V型电热驱动器的诸多理论研究均采用以下方法，即只考虑单向耦合作用，依次分别建立电-热和热-力耦合子模型，并根据电-热模型得到的温度结果计算驱动器的膨胀变形，将其代入热-力模型最终得到驱动器位移.针对电-热耦合子模型，文献[4]基于能量守恒原理，构建V型电热驱动器的瞬态电热偏微分方程，并借助有限差分法进行求解.文献[5]分别考虑真空和空气情况下的热损失效应，建立了V型电热驱动器一维和瞬态模型.采用分离变量法分离出模型中的时间项，获得稳态模型.通过Fourier级数结合加权余量法对稳态模型求解，最终得到含时间指数项和含空间三角函数项的瞬态温度解.文献[6]将V型电热驱动器简化成3个集成单元，根据等效电流法建立驱动器瞬态电-热模型，最终获得各个单元的平均温度.在热-力耦合子模型方面，文献[7]根据V型电热驱动器的对称性和Castigliano定理建立热力耦合模型.文献[8]基于虚功原理将V型电热驱动器一侧的约束用力和力矩代替，建立了驱动器热-力模型，并用有限元(FEM)仿真进行验证.文献[7]认为V型电热驱动器的应变是由于受热和力作用导致的，然后基于Euler-Bernoulli梁理论得到V型电热驱动器热-力耦合方程.通过对方程进行单元离散，并假设每个单元解的形式为Hermitian形函数，使用Galerkin法求得驱动器位移.文献[9]假设V型电热驱动器中存在自由热膨胀变形，即不考虑热变形伸长而产生的反力作用，根据超静定原理和Pythagoras定理获得驱动器的稳态位移.而在V型电热驱动器的动态特性方面，目前主要研究其在恒定加载电压下，位移随时间的变化关系.这远远无法满足电热驱动器在精密快速定位[10-11]、微夹钳[12-13]等一系列应用中的需求.

本文首先提出一种正弦变换结合隐式差分的方法，用于求解V型电热驱动器瞬态电-热模型中的偏微分方程.同时，基于受迫振动理论建立V型电热驱动器热-力模型，计算获得V型电热驱动器的位移.然后，对驱动器理论模型的计算进行收敛性分析，获得最大计算收敛步长.接着，使用有限元仿真对V型电热驱动器的瞬态、稳态温度和位移进行验证，同时通过实验验证V型电热驱动器理论模型下的位移.最后，研究V型电热驱动器在变电压下的动态响应特性.本文研究可为V型电热驱动器的优化设计及控制研究提供理论依据.

1 电热耦合模型

1.1 能量守恒方程

V型电热驱动器的长度远大于其宽度和厚度，V型电热驱动器可以被简化成一维模型，如图1所示.其中：L为驱动器的长度；b为驱动器宽度；d为驱动器厚度；θ0为驱动器弯曲角度；g为驱动器与基底间的距离；x为微元的位置；dx为微元的长度；T(x,t)为驱动器上关于位置x和时间t的温度函数.

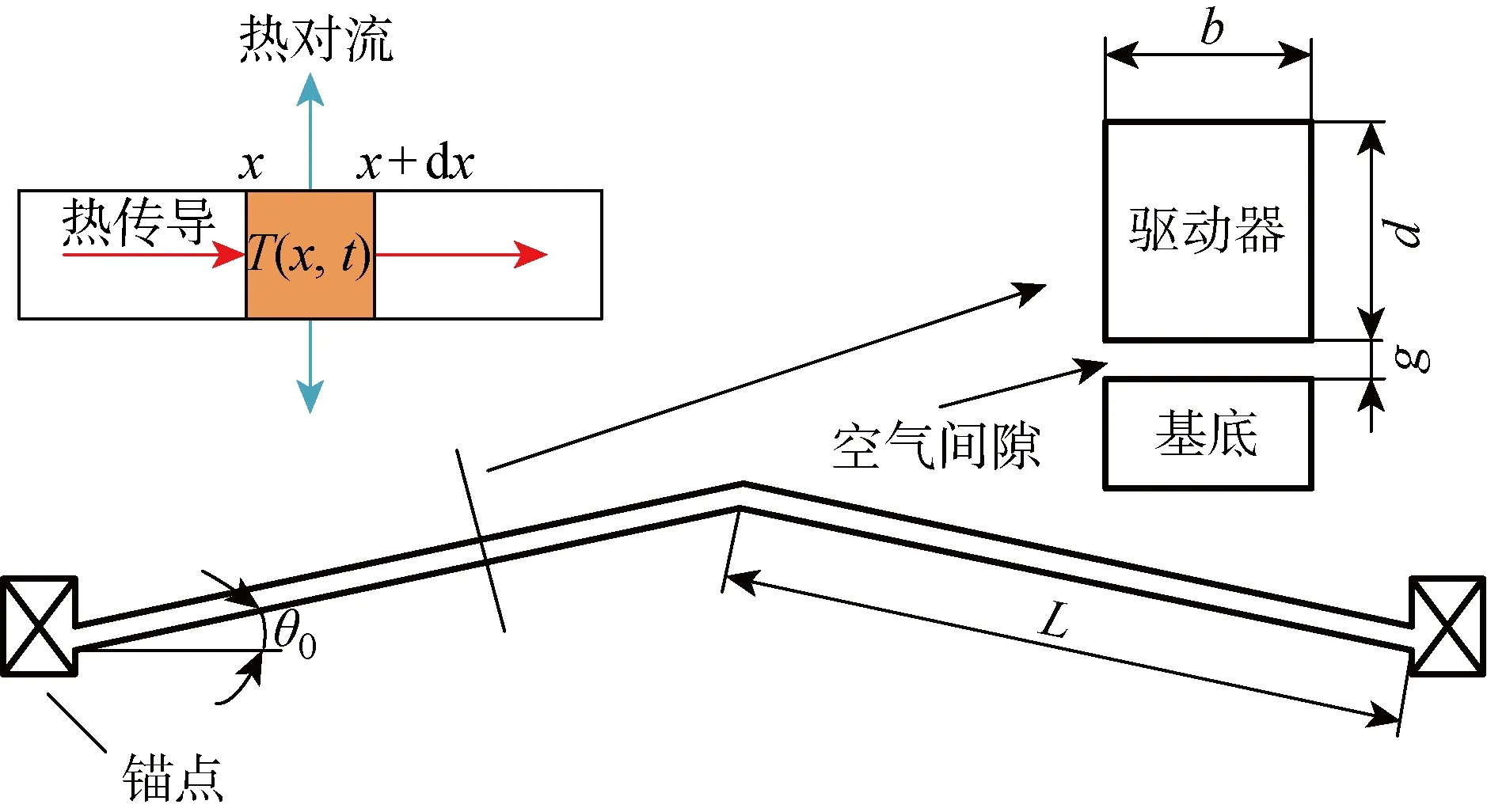
图1 V型电热驱动器结构Fig.1 Structure of V-shaped electrothermal actuator

取驱动器上一微元dx进行传热分析，以热传导的方式流入微元热量Qin、流出微元热量Qout，可以表示为

(1)

(2)

式中：κ为硅的热传导率；T为温度函数T(x,t)的简写形式.

微元热对流Qco以及与基地间的热损失Qlo分别为

Qco=kv(T-T0)(b+2d)Δx

(3)

Qlo=ks(T-T0)bΔx

(4)

式中：T0为室温；kv为驱动器表面与空气的热对流系数；ks为驱动器表面和基底之间的形状热损失系数，由文献[14], 这里ks取为 6 000 W/(m2·K).微元焦耳热可以表示为

Qg=J2ρbdΔx

(5)

式中：J为电流密度；ρ为掺杂硅的电阻率.综合式(1)～(4)并根据能量守恒原理可以得到,电热驱动器的瞬态偏微分方程如下所示:

(6)

式中：c为硅的比热容；ρd为硅密度.由于驱动器两侧与锚点连接，所以其边界条件和初始条件分别为

(7)

T(x,0)=T0

(8)

1.2 稳态分析

通过整理式(6)并简化得到驱动器的稳态传热微分方程如下所示：

(9)

式中：Ta为绝对温度.正弦变换可用于求解满足边界条件为0的微分方程[15-16]，离散型正弦变换的正、反变换公式分别表示为[15]

(10)

n=1,2,…,N

(11)

i=1,2,…,I

首先，对式(9)进行差分离散，可以得到：

(12)

式中：Δh为空间步长.这里令正弦变换中I=N，根据式(11)，Ta,i可表示为

(13)

进一步，Ta,i+1+Ta,i-1可变换为

Ta,i+1+Ta,i-1=

(14)

将式(13)和(14)代入式(12)，整理得到：

(15)

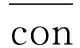
kv(b+2d)/(bd)+ks/d}

(16)

1.3 瞬态分析

根据式(6)，简化得到驱动器的瞬态方程为

(17)

对该方程进行差分离散，其中，时域采用隐式差分形式，可以得到：

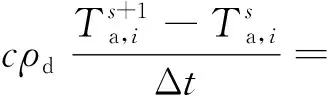
(18)

式中：Δt为时间步长；s为时间步序号.类似地，式(18)可以变换为

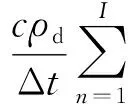
(19)

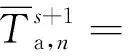
kv(b+2d)/(bd)+ks/d

(20)

1.4 收敛性分析

根据前文所述方法，V型电热驱动器的温度分布可看作是一系列正弦波叠加的结果.V型电热驱动器上离散点越多，所叠加的正弦波个数也就越多，得到的结果也就越接近于真实解，但同时也会导致求解时间的急剧增加.因此，合理的步长既能保证求解精度，也能提高计算效率.所用V型电热驱动器的材料为硅，其尺寸和材料参数分别如表1和2所示.其中：α为热膨胀系数；E为弹性模量；μ为泊松比.为进行收敛性分析，首先选取通过251个离散点计算得到的V型电热驱动器稳态温度作为参考温度，分别通过11、21、31、51个离散点计算得到的驱动器稳态温度与参考温度的差值如图2所示，其中：e为温度误差.从图2中可以看出， 随着离散点数的减小，温度误差越来越大，最大的温度误差约为8 K.在驱动器上，温度误差总体呈现由中心往两侧递减的趋势.51个离散点的温度误差十分微小，可忽略不计.因此，当离散点数不少于51个时，驱动器温度计算结果即可认为收敛.综合考虑计算精度和时间成本，选择251个离散点用于V型电热驱动器的温度分布计算.

表1 V型电热驱动器尺寸参数

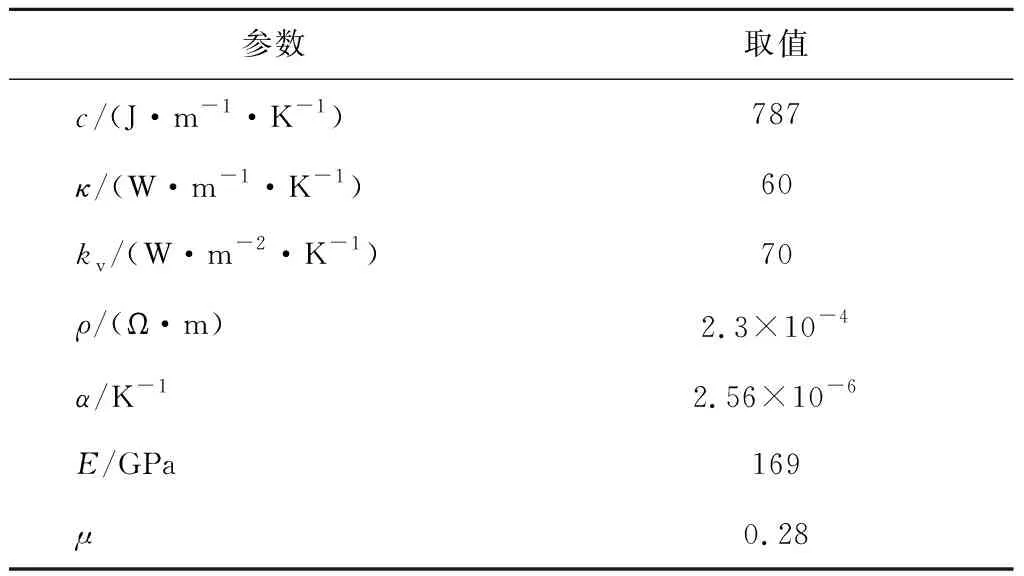
表2 硅的材料参数Tab.2 Material parameters of silicon

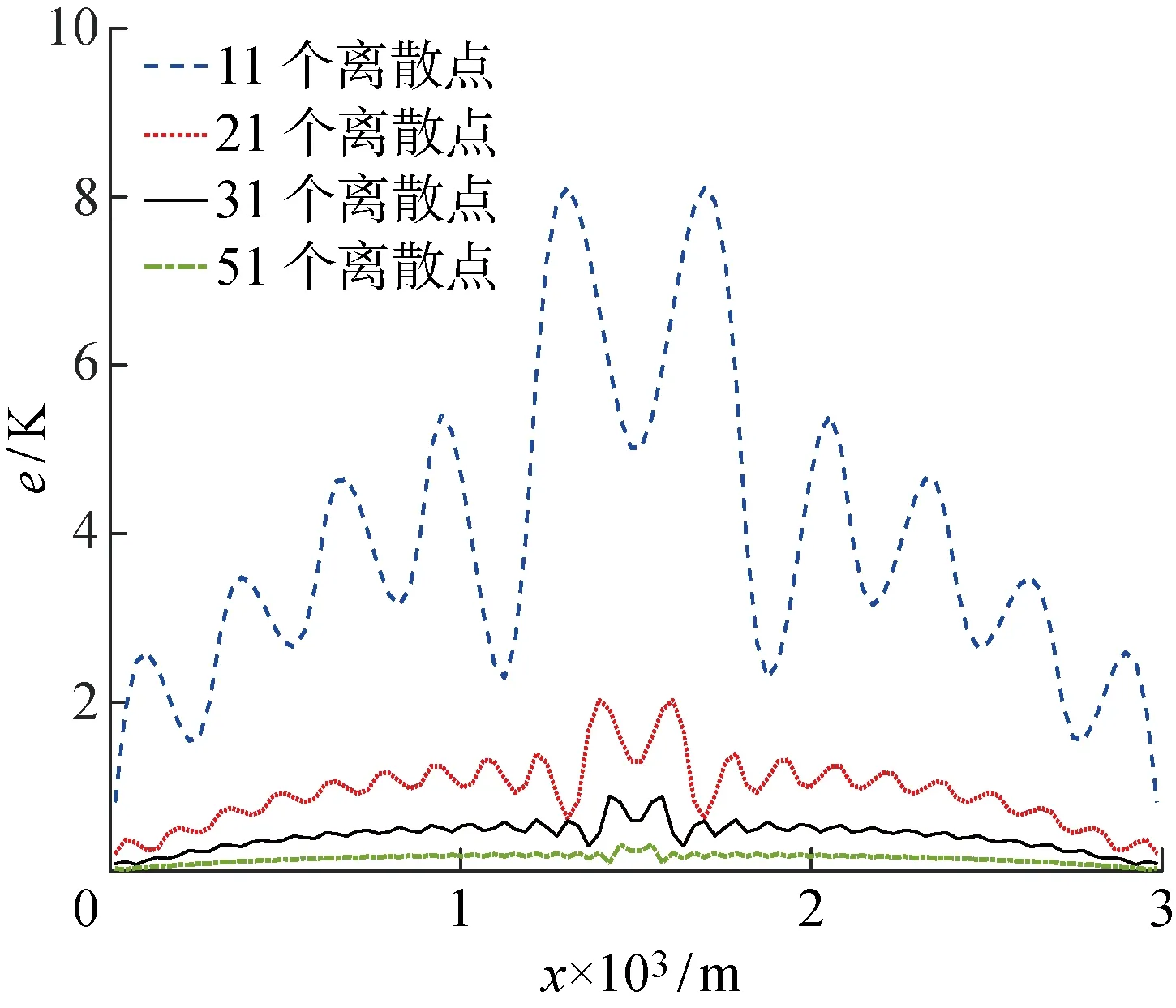
图2 不同离散点数的V型电热驱动器温度计算误差Fig.2 Temperature calculation errors of V-shaped electrothermal actuator at different discrete points

2 热力耦合模型

由于V型电热驱动器的长度远大于其宽度和厚度，所以可将驱动器视为简支梁.将其中心处的位置变化作为其位移，即驱动器上的最大位移.由于该位移相对较小，可将其等效成离散振动系统.在此基础上，为进一步简化模型，忽略振动系统中的阻尼集中参数元件.该模型的详细推导可以参考文献[17],此处不再赘述.V型电热驱动器的受迫振动方程[18]如下所示：

(21)

(22)

式中：Δlt为当前时刻热膨胀变形，可根据文献[17]计算得到；A为驱动器的横截面积；θ(t)为当前时刻t的V型电热驱动器弯曲角度.

3 模型验证

由正弦变换计算得到的16 V电压下，驱动器在0～200 ms内的瞬态温度云图如图3所示.在驱动器上共选取251个离散点用于温度分布计算.从图3中可以看出，初始时刻V型电热驱动器上的温度变化较快.V型电热驱动器中间位置温升较快，两端温度变化缓慢，这是由于中心处的热损失较于两侧边界相对较小.

不同时刻驱动器上的温度分布曲线如图4所示.从图4中可以明显看出，随着时间的增加，驱动器上不同点处的温度差异有所增大；V型电热驱动器在t=50 ms时的温度分布即趋近于稳态下的温度分布，这与瞬时温度云图中驱动器温度分布(见图3)在t=50 ms之后几乎没有变化的现象一致.

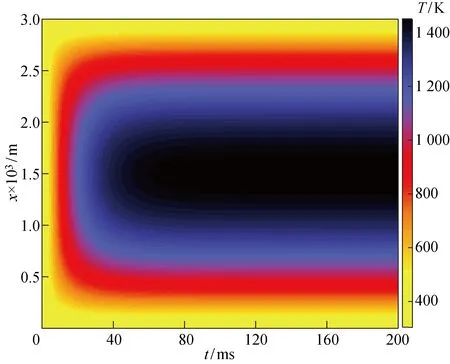
图3 16 V电压下V型电热驱动器的瞬态温度分布Fig.3 Transient temperature distributions of V-shaped electrothermal actuator at 16 V

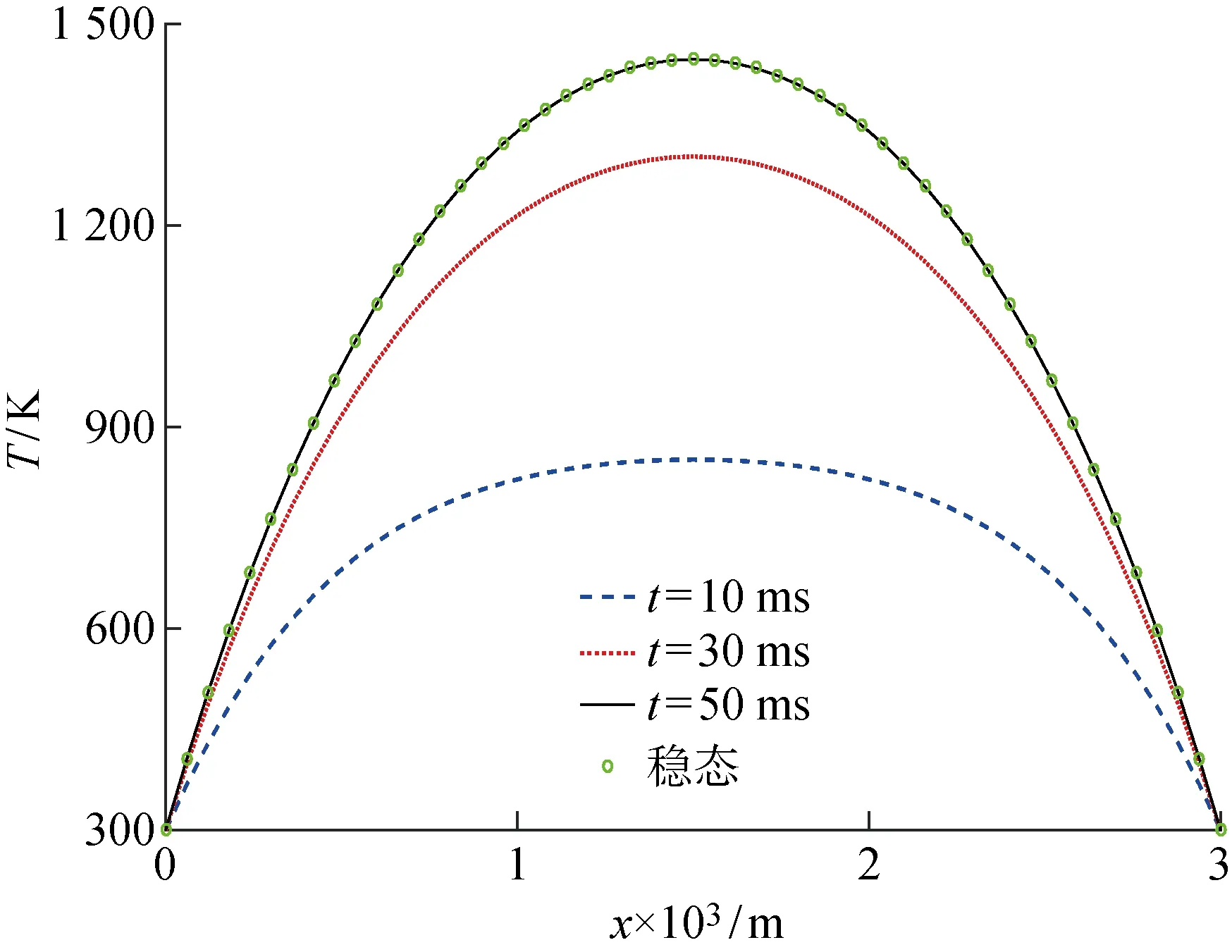
图4 16 V电压下不同时刻的V型电热驱动器的温度分布Fig.4 Temperature distributions of V-shaped electrothermal actuator at different times and 16 V

3.1 仿真验证

在有限元软件中，建立V型电热驱动器的三维模型，如图5所示.首先，选择Solid226电-热-力耦合单元对驱动器的几何模型进行网格划分.其次，在锚点处分别加载恒温和电压条件.接着，对驱动器各个面分别施加热对流条件，底面的对流系数为ks，其他面的对流系数为kv.最后，设置热、力及变形收敛容差，并进行求解和后处理.

图5 V型电热驱动器有限元模型Fig.5 FEM model of V-shaped electrothermal actuator

16 V电压下，理论、仿真模型获得的不同时刻驱动器的温度分布如图6所示.由图6可知，总体上，理论模型的温度计算结果与仿真结果几乎一致.但在初始时刻，理论模型的计算温度稍大于仿真温度；随着时间的增加，两者的温度差异越来越小.这主要是由于理论模型中对时域的离散采用隐式差分法，该方法的精度只有1阶；而在有限元软件中一般使用Runge-Kutta法处理时域，该方法精度很高.同时，理论计算采用的是一维简化模型，而仿真中建立的V型驱动器模型更为完整.16 V电压下，理论与仿真模型的瞬态温度差值云图如图7所示.由图7可知，最大温度差发生在初始时刻，约为35 K，且初始时刻温差较大， 这进一步验证了图6中温差随着时间的增加而减小的结论.V型电热驱动器两端的温差较大，这是由于驱动器两端的温度梯度大于中间的温度梯度，而理论模型中的离散点数小于有限元模型造成的，理论计算的温度结果误差较大.

图6 16 V电压下不同时刻的V型电热驱动器理论和仿真温度分布对比Fig.6 Theory and simulation temperature distribution differences of V-shaped electrothermal actuator at different times and 16 V

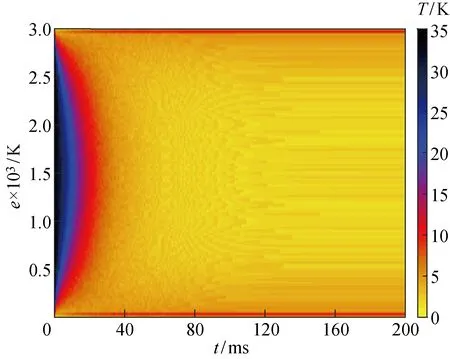
图7 16 V电压下V型电热驱动器的理论和仿真瞬态温度差值分布Fig.7 Theory and simulation transient temperature distribution differences of V-shaped electrothermal actuator at 16 V

不同加载电压下，通过理论和仿真模型计算得到的V型电热驱动器的稳态温度分布如图8所示，其中：U为电压.由图8可知，驱动器稳态下的温度计算结果与仿真结果完全一致；随着电压的升高，驱动器的最高温度急剧增加.V型电热驱动器在14 V和16 V电压下的瞬态理论和仿真位移如图9所示.其中：y为瞬态位移.从图9中可以看出，理论和仿真位移较为接近.由于在初始时刻的理论温度大于仿真温度，导致理论计算位移在初始时刻也同样大于仿真位移.

图8 不同电压下V型电热驱动器的理论和仿真稳态温度分布Fig.8 Theory and simulation static temperature distributions of V-shaped electrothermal actuator at different voltages

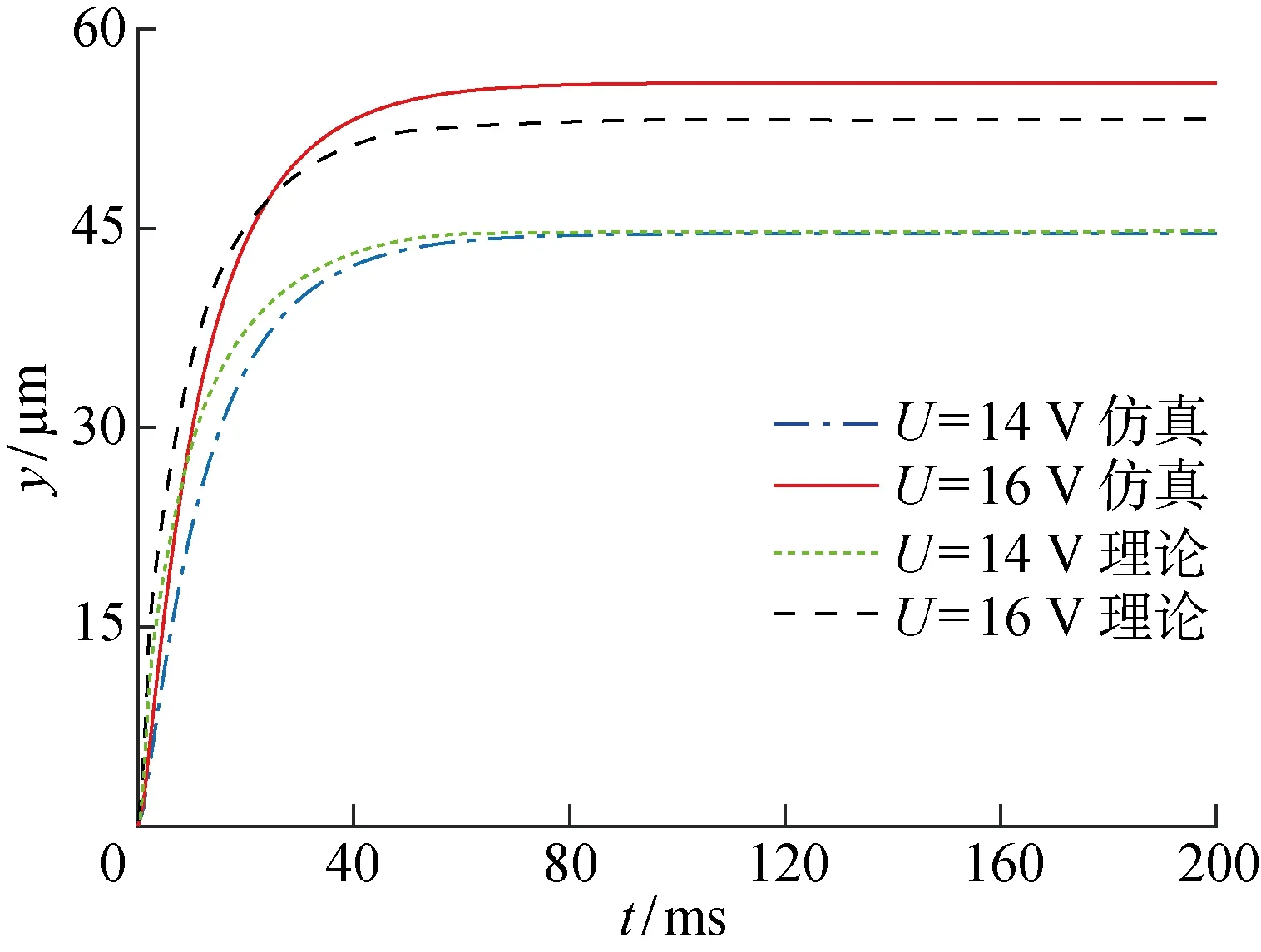
图9 14 V和16 V电压下V型电热驱动器的瞬态位移Fig.9 Transient displacements of V-shaped electrothermal actuator at 14 V and 16 V

3.2 实验验证

V型电热驱动器的加工采用反应离子干法深刻蚀工艺[19-20]，主要包含刻蚀、键合、溅射等步骤.经划片、封装和引线后，最终如图10所示.

图10 封装芯片结构Fig.10 Structure of packaged chip

驱动器位移测量实验装置如图11所示.通过实验装置，获取不同加载电压下的驱动器稳态时的图像.首先，对图像进行灰度化处理，接着对图像中驱动器的中心区域使用边缘检测算法[21]，获得驱动器中心区域的轮廓特征,如图12所示.从图12中可以明显看出，0 V电压下驱动器中心到边框左侧框线的距离g0远大于16 V电压的距离g1.根据驱动器中心与边框左侧框线的相对位置变化，可得到不同电压下V型电热驱动器的位移，如图13所示.其中.经过对标尺(边框)的计算，图像中一个像素代表3.9 μm, 因此实验测量位移存在上下3.9 μm 的偏差.从图13中可以看出，不同电压下，驱动器理论、仿真和实验的稳态位移总体保持一致，理论和仿真位移结果在合理的实验测量误差范围之内.

图11 V型电热驱动器位移测量实验装置Fig.11 Experimental setup for measuring displacement of V-shaped electrothermal actuator

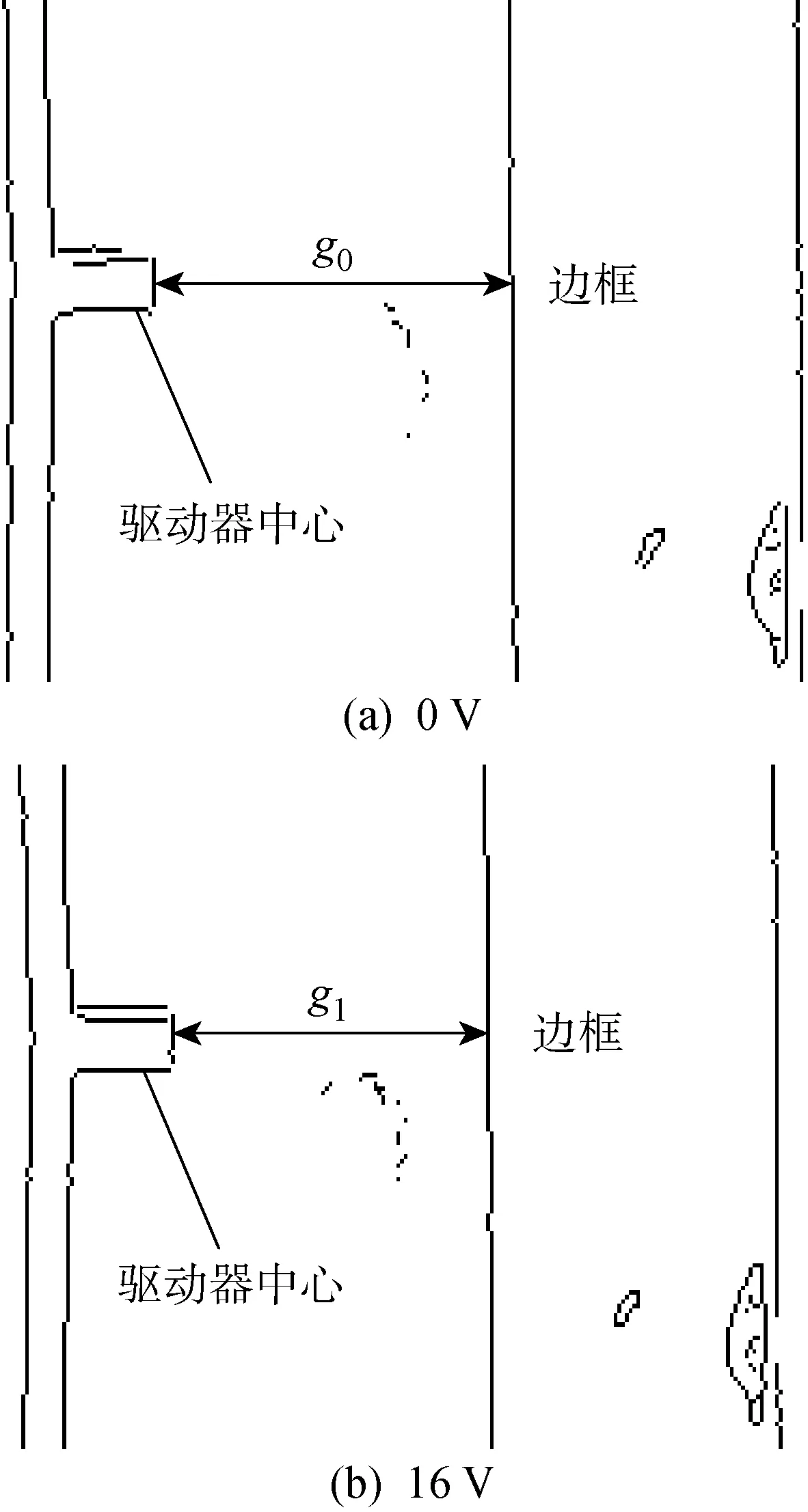
图12 0和16 V电压下V型电热驱动器图像的中心区域轮廓特征Fig.12 Contour feature pictures in the middle of V-shaped electrothermal actuator at 0 V and 16 V

图13 不同电压下V型电热驱动器的理论、仿真和实验稳态位移Fig.13 Theory, simulation, and experiment steady state displacements of V-shaped electrothermal actuator at different voltages

4 动态特性分析

由图13可知，V型电热驱动器的加载电压直接决定了其位移的大小.通过不断改变电压值即能够实现对驱动器运动的有效控制.因此，基于上述方法所建立的多物理场耦合模型，分析驱动器在变电压下的动态特性可为驱动器制定合理的位移控制策略提供理论支撑.这里选取两种典型电压信号(阶跃和正弦偏置电压)，分别研究V型电热驱动器在其作用下的温度和位移响应特性.

在阶跃电压下，V型电热驱动器的中心温度和位移随时间的变化曲线如图14所示.从图14中可以看出，驱动器的温度和位移均在50 ms时达到最大值;当结束电压加载后，驱动器中心处的瞬态温度和位移急剧下降，随着时间的不断增加，温度和位移的变化逐渐平缓.

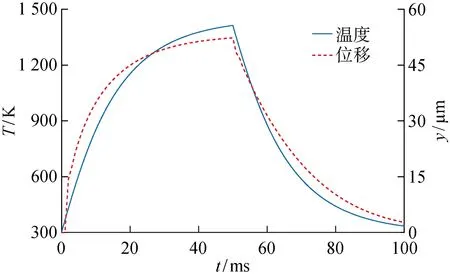
图14 阶跃电压下V型电热驱动器中心温度的瞬态温度和位移Fig.14 Transient temperature and displacement in the middle of V-shaped electrothermal actuator at step voltage

不同正弦偏置电压下，电热驱动器的瞬态温度和位移如图15所示.由图15可知，当正弦电压作用时间大于5个周期，即50 ms后，驱动器中心处的温度与位移也呈现正弦波形变化.此时，驱动器中心处的温度与位移的平均值均等于驱动器在等效直流电压作用下的稳态温度和位移.正弦电压幅值越大，驱动器中心处的温度与位移的变化幅度也就越大.因此，在周期性加载电压作用下，电热驱动器中心处的温度呈现周期性变化，电热驱动器的位移变化最终也近似周期运动，且运动变化周期与电压变化周期相同.

图15 不同正弦偏置电压下V型电热驱动器中心处的瞬态温度与位移Fig.15 Transient temperature and displacement in the middle of V-shaped electrothermal actuator at different sine bias voltages

5 结论

(1) 本文建立了V型电热驱动器多物理场耦合模型，使用正弦型变换结合隐式差分法求解驱动器电-热耦合偏微分方程；经过稳定性测试发现, 该方法在求解时具有良好的收敛性；基于振动理论建立热-力耦合模型.

(2) 基于电-热模型得到的不同电压下的驱动器瞬态和稳态温度分布与有限元仿真结果几乎一致；而基于热-力模型得到的不同电压下的驱动器稳态位移与实验、仿真结果也几乎一致.

(3) 在周期性电压下，V型电热驱动器最终也呈现周期性运动，且两者周期相等.