环柱式天线展开过程耦合动力学分析

张大羽，马小飞，王 辉，罗建军，李 洋，范叶森

(1. 中国空间技术研究院西安分院，西安 710100；2. 西北工业大学航天学院，西安 710072)

0 引 言

空间大型可展开结构的优势在于可提高信息传输的容量，为其在空间发电、深空探测等领域提供了潜在的应用前景。由于受火箭运载能力和运载空间的限制，大型可展开结构必须具有可折叠、可展开的能力。空间环柱式天线以高收纳比、质量轻、展开稳定性好等优点，成为目前大型甚至超大型星载可展开结构的最佳结构形式。

20世纪80年代，美国NASA Langley研究中心首先提出了空间环柱式天线的设计概念。随后，他们研制了大口径工程样机，并进行了相应的地面测试。近两年国外航天界对空间环柱式天线又重视起来，美国Harris公司研制了小口径的空间环柱式天线，并应用在微小卫星系统，展现出较大的应用价值。环柱式天线主要由斜拉绳索、环形桁架和中心柱三部分组成，其中桁架由绳索吊装连接于中心柱上。环柱式天线展开过程的特色是绳索释放运动与桁架展开之间的非线性耦合动力学行为。这个过程中，绳索与桁架是连接关系，对桁架展开过程提供一定的刚度，起到维持桁架构形稳定的作用。但是过大的绳索张紧力对桁架展开起到径向力回收的作用，会阻碍展开的稳定性。因此，绳索对环柱式天线的顺利展开具有至关重要的影响。

由于受到地面试验等因素的限制，对大型空间可展开结构的展开过程进行理论和仿真分析是了解和改善其动力学特性最为有效的手段。1)对于大型空间可展开结构，一般而言是反射器口径大于等于4 m，需要设计复杂展开成形的柔性工作面的结构类型。由于这类结构尺度大，柔性效应显著，展开阶段动力学分析难点是柔性部件在展开过程中存在大位移、大转动和大变形，导致结构的刚体运动与柔性变形间发生明显的耦合效应。已有文献对刚体或者小变形的空间可展开结构进行仿真，但这类方法无法用于大型可展开结构的分析，必须采用可准确描述柔性体大变形的分析方法，这类典型的分析方法有绝对节点坐标法、几何精确梁方法、公旋坐标法，例如，文献[13-15]采用绝对节点坐标方法分别建立了大型环形桁架结构、百米尺度的空间电站以及UltraFlex太阳翼动力学模型，分析了展开过程中的结构大变形特性。文献[16-18]采用几何精确梁理论系统性地分析了大型圆形、椭圆形桁架结构的展开动力学行为，分析了桁架展开过程中的索网大变形特性。文献[19]基于共旋坐标法建立了大变形柔性太阳电池阵的多体模型，分析了电池阵复杂的展开动力学现象。2)对于环柱式天线，从公开发表的文献来看，关于这类结构的动力学研究报道主要针对展开后服役阶段的结构模态特性进行分析，而没有针对展开过程进行研究。环柱式天线展开过程的动力学特点主要体现在以下两点：首先，该结构属于大型空间可展开结构的一种设计类型，同样存在展开过程中大位移、大转动、大变形问题，需要采用具有描述大变形能力的多柔体分析方法对其展开过程进行动力学仿真分析。其次，环柱式天线的环形桁架展开过程中，与桁架连接的斜拉索随之释放。该过程中斜拉索的拉力对桁架的展开起到阻力作用，动力学特点是桁架向外径向伸展运动与斜拉索向内径向阻力牵引之间的非线性耦合行为。文献[22-23]对环形天线的绳索伸展机构进行了仿真，但绳索在环形天线中作为动力绳，与本文环柱式天线中绳索的作用不同。在环柱式天线中，绳索(斜拉索)在桁架展开过程可以提供一定的刚度，维持桁架构形稳定，因此绳索对桁架的顺利展开起到至关重要的作用。

本文针对环柱式天线展开过程中的动力学特性进行研究，采用非线性欧拉梁单元模拟斜拉绳索，几何精确梁单元模拟桁架，集成了一套可描述以“斜拉绳索释放运动-环形桁架展开运动”为特点的耦合动力学仿真平台搭建方法；探究了绳索特性(弹性模量、绳索直径和绳索数量)对环形桁架展开过程的影响，并提出了对绳索参数设计的优化思路；所搭建的仿真平台可准确地描述绳索释放运动与桁架展开运动之间的耦合动力学行为，可为环柱式天线的设计和研制提供重要的理论依据。

那么〈wi,vj〉=δij(i,j=1,2,3,4,5)，则根据引理3，可得由span{w1,w2,w3,w4,w5}张成的另一补空间.最后可将(1)式简化成：

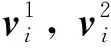
1 环柱式天线展开动力学模型

1.1 模型描述

环柱式天线由可展开的环形桁架、中心柱、斜拉绳索和反射网组成。环形桁架由若干杆件构成，收拢时可将桁架折叠起来，展开时由桁架的展开机构将其展开成一个圆环。本文不考虑反射网，重点研究环形桁架的展开过程。该过程的动力学特点为桁架向外径向伸展运动与斜拉索向内径向阻力牵引之间的非线性耦合行为，因此可将其描述为杆系结构(环形桁架)与张力结构(斜拉索)之间耦合。

环柱式天线可分解为多个“V字型”单元，每个单元中包括绳索和桁架杆件，如图1所示。其中绳索的一端通过旋转副与桁架杆件连接，另一端与中心柱连接。系统由多个刚体和柔性体部件组成，部件之间的连接通过多种约束实现，例如：球副主要用于绳索与桁架杆件之间，以及绳索与中心柱之间的连接。旋转副、耦合副及同步齿轮副用于桁架杆件间的连接。移动副用于铰链与中心柱之间的连接。

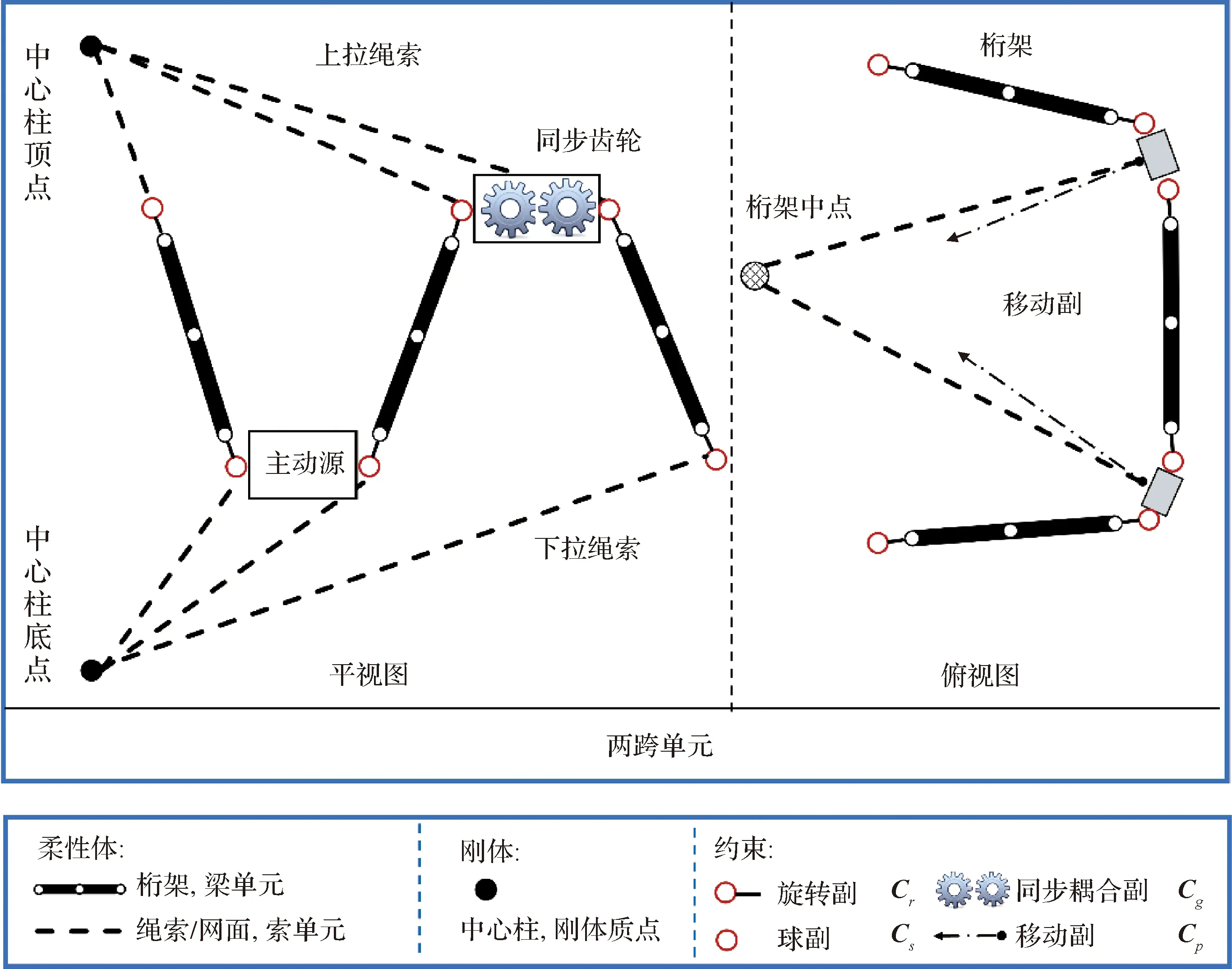
图1 环柱式天线多体模型Fig.1 Multibody model of rod-cable antenna

值得说明的是，本文采用移动副用于提升桁架的展开同步性，该约束副的作用方向为从每个铰链中点指向中心柱中点。环柱式天线的主动源驱动为桁架上的蜗轮蜗杆电机。

1.2 系统控制方程

在环柱式天线的多体模型中，前后斜拉索采用非线性欧拉梁单元建模，环形桁架采用几何精确梁单元建模。旋转副、同步齿轮副、球副和移动副采用约束方程描述。中心柱采用质点描述。通过多柔体动力学理论，将环形桁架、绳索、中心柱质点模型以及运动约束方程进行组装，得到环柱式天线的微分-代数方程组：

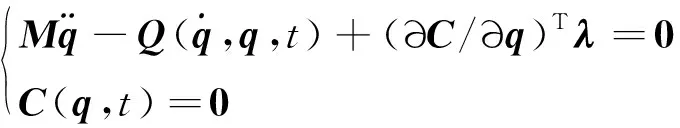
(1)

环柱式天线的展开过程分为预展过程和电机驱动展开过程。本研究不考虑预展过程，重点关注电机驱动展开过程。电机展开阶段，其中电机安装于桁架杆件之间，电机驱动设计采用角度驱动形式，角度驱动函数设计如下：

大数据背景下，企业会计信息不仅完善了数据共享功能，在各企业单位的具体交流上也密切起来，实现了企业及单位共享信息平台建设，解决了财务信息“孤岛”的问题。同时，大数据背景下的企业会计信息化建设能提高企业的重视程度，减少中小企业会计信息化实现程度参差不齐的问题，实现企业各部门、企业与企业间良好的信息共享和运行循环。

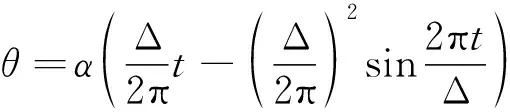
(2)

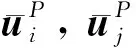
1.3 绳索建模

绳索建模采用Dombrowski建立的非线性绝对节点坐标欧拉梁单元，该单元可准确表征其大位移、大转动、大变形，适用于描述斜拉索的运动和变形特点，如图2所示。

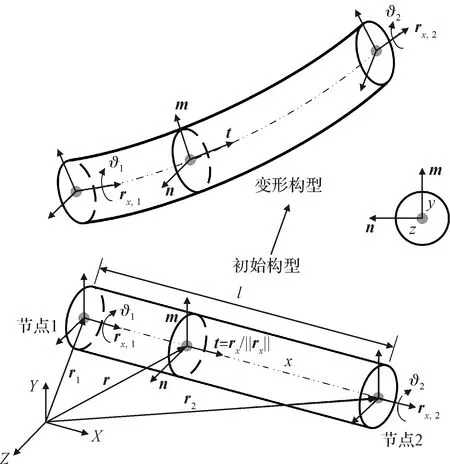
图2 非线性欧拉梁单元Fig.2 Nonlinear Euler beam element

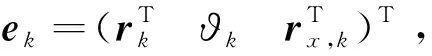
青樱望着窗外深沉夜色，紫禁城乌漆漆的夜晚让人觉得陌生而不安，檐下的两盏白灯笼更是在夜风中晃得让人发慌。青樱打断阿箬：“好了。有这嘴上的功夫，不如去倒杯茶来我喝。”

(3)

图4为桁架展开口径与高度分析。首先，本文模型计算的结果表明，环形桁架分别从预展阶段口径5 m和高度0.3774 m变化到最终展开口径10 m和高度-0.3774 m，实现了环柱式天线的顺利展开，证明了本文模型在运动学上的准确性。值得说明的是在展开高度方面，由于下铰链施加径向移动副确保展开的同步性，导致下铰链无法在高度方向运动，因此桁架在高度方向上的运动为上铰链向下铰链运动，数值上体现为正向0.5倍的预展高度(0.3774 m)变化到负向0.5倍的预展高度(-0.3774 m)。

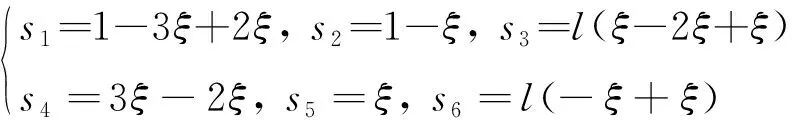
(4)

式中：,,分别是桁架中相邻杆件、杆件、以及中间连接齿轮在耦合副参考点的向量。

2.1 两组孕妇妊娠指标比较 FGR组新生儿出生体质量、身长、头围等体格指标均显著低于对照组，差异均有统计学意义(P<0.05)。FGR组胎盘重量明显低于对照组，差异有统计学意义(P<0.05)。见表1。

选取一、二期沥青心墙接头高程4 046 m处为典型剖面进行应力应变计算，计算剖面桩号0+661.45 m。

毫无疑问，数学史融入数学教学实践会对学生的数学学习产生影响，此方面的研究大都依托于具体的教学主题，通常附属于HPM教学实践，在数学史融入数学教学实践后对融入效果进行测评，以此看对学生数学学习的影响．例如报告11在数学史融入对数教学实践后，研究者用学生课上对工作单的作答、小组及全体讨论的录音及课后两份匿名的问卷来评估学生知识的获得及学生对使用数学史的意见等．报告17中，研究者用前后测、田野观察及最后的问卷来评估实践效果．

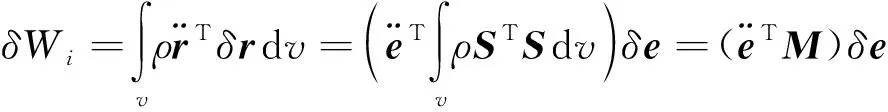
(5)

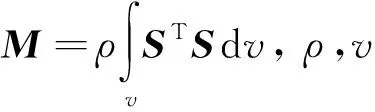
2022年杭州亚运会皮划艇、赛艇项目选址富春江,做好浮标站相关要素的分析研究,也是为亚运会精细化预报预警服务提供一些理论基础。

欧拉梁单元的应变能可定义为：

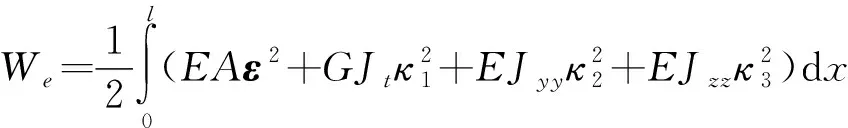
(6)

式中：,,分别为单元的弹性模量、横截面积、剪切模量;为单元的截面极惯性矩;,分别为关于轴和轴的截面惯性矩。

对于轴向应变，其表达式为：

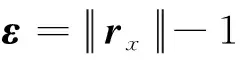
(7)

对于空间曲率，可定义为：

(8)

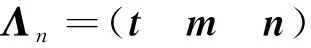
Monographic report: Application of ultrasonography in diagnosis of tuberculosis

(9)

式中：( )′=dd。

1.4 约束方程

环柱式天线建模中分别采用了旋转副、球副、移动副和同步齿轮副，如图3所示。本小节分别介绍这4种约束副,,,的数学形式。

1)旋转副

桁架杆件与刚体铰链之间采用旋转副连接，实现展开过程中杆件的相对转动，旋转副的作用是仅能使得两个杆件沿着固定的转动轴旋转，如图3(a)所示，其约束方程为：

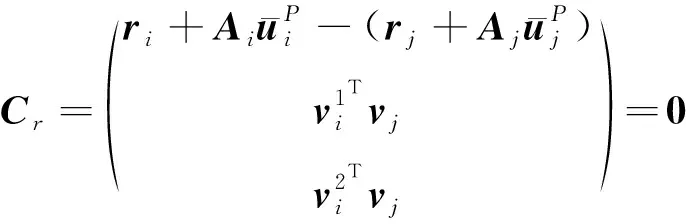
(10)

式中：Δ为仿真总时长，为时间，为展开角度系数。设定电机将桁架从预展口径5 m驱动展开到最终口径10 m。在这种情况下，桁架中每个杆件角度变化为∈(π6, π2)，因此展开角度系数为=2π/3Δ。

⑤ 暗喻俄国十月革命。十月革命是根据俄历命名的，俄历的1917年10月25日，即是西历1917年11月7日。

酒评：赤霞珠和西拉的混酿，在全世界都非常受欢迎，从1960年至今，酿造从来未停止，被称为“小葛兰许”，非常成功和受欢迎的一款红酒。Bin 389是集南澳各大优质产区之精华的跨区混酿，极具陈年能力。从有换塞诊所以来，全世界很多奔富的酒友收藏了很多老年份的389，状态依然很好。以酿造Bin 707和Grange用过的桶来陈酿，小部分新桶，比例因年份而异。

2)球副

由图1可知，人民币汇率政策的变动会以汇率为中介变量，对进出口贸易和国际资本流动产生影响，二者的变动通过国际收支途径体现为外汇储备的波动，进而通过外汇占款对国内货币供给量产生影响，继而影响物价、社会需求、经济增长等宏观经济变量。这些变量的波动必然影响下一步汇率政策的选择。可见，汇率政策选择和制度改革与宏观经济两者相互影响，互为扰动因素。

斜拉绳索与中心柱、绳索与桁架之间采用球副连接。球副的作用是约束两个物体之间的所有位移，但两个物体可以在空间三个方向上转动，如图3(b)所示，其约束方程为：

=-=

(11)

式中：,分别是中心柱质点模型和绳索单元、桁架单元和绳索单元的球副参考点在全局坐标系的位置。

欧拉梁单元惯性力的虚功可定义为：

3)移动副

中心柱中点与铰链中点之间采用移动副连接，实现铰链只能沿着径向滑移，从而达到提升桁架展开同步性的目的。移动副的作用是约束两个物体之间的所有转动和两个方向的位移，物体之间只允许沿着固定方向移动，如图3(c)所示，其约束方程为：

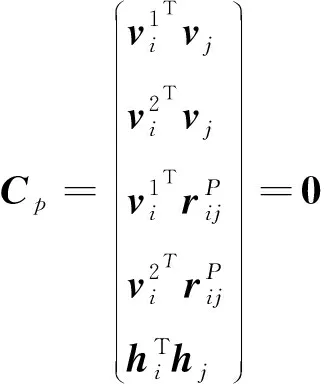
(12)

对比分析2014年9月—2015年8月中国大陆IMERG和CGDPA日平均降水量,结果表明:两者的空间分布比较一致,东部介于1～10 mm,西部介于0.1～5 mm,南部介于2～10 mm,北部介于0.1～5 mm,说明IMERG日平均降水量能够较好地反映中国大陆降水量西部少、东部多,南部多、北部少的特点;IMERG日平均降水量比CGDPA的空间分布连续性更好,尤其是在西部、北部等地面雨量计观测站点较少的地区(图1)。西藏东南部、新疆天山,以及青海、广西和广东南部和海南等地区,IMERG日平均降水量比CGDPA偏低。

4)同步齿轮副

我国的碳信息披露尚处于初步发展阶段，要结合经济发展的时代特点，充分借鉴国外碳会计研究的优秀理论成果，全面理解碳会计制度。从多角度分析碳信息的归类分配方式，找出有决定性的碳信息分类项目，深入探究碳披露知识，结合具体国情不断创新，建设具有中国特色的碳会计制度，使碳披露具有可操作性。

在环柱式天线中，同步齿轮位于桁架杆件接头处，要实现同步齿轮的功能，只需将相邻两个杆件和接头之间的转动副定义为耦合副即可，实现同一接头处的杆件转动角度相同，从而达到同步齿轮的目的，如图3(d)所示。同步齿轮副的约束方程为：

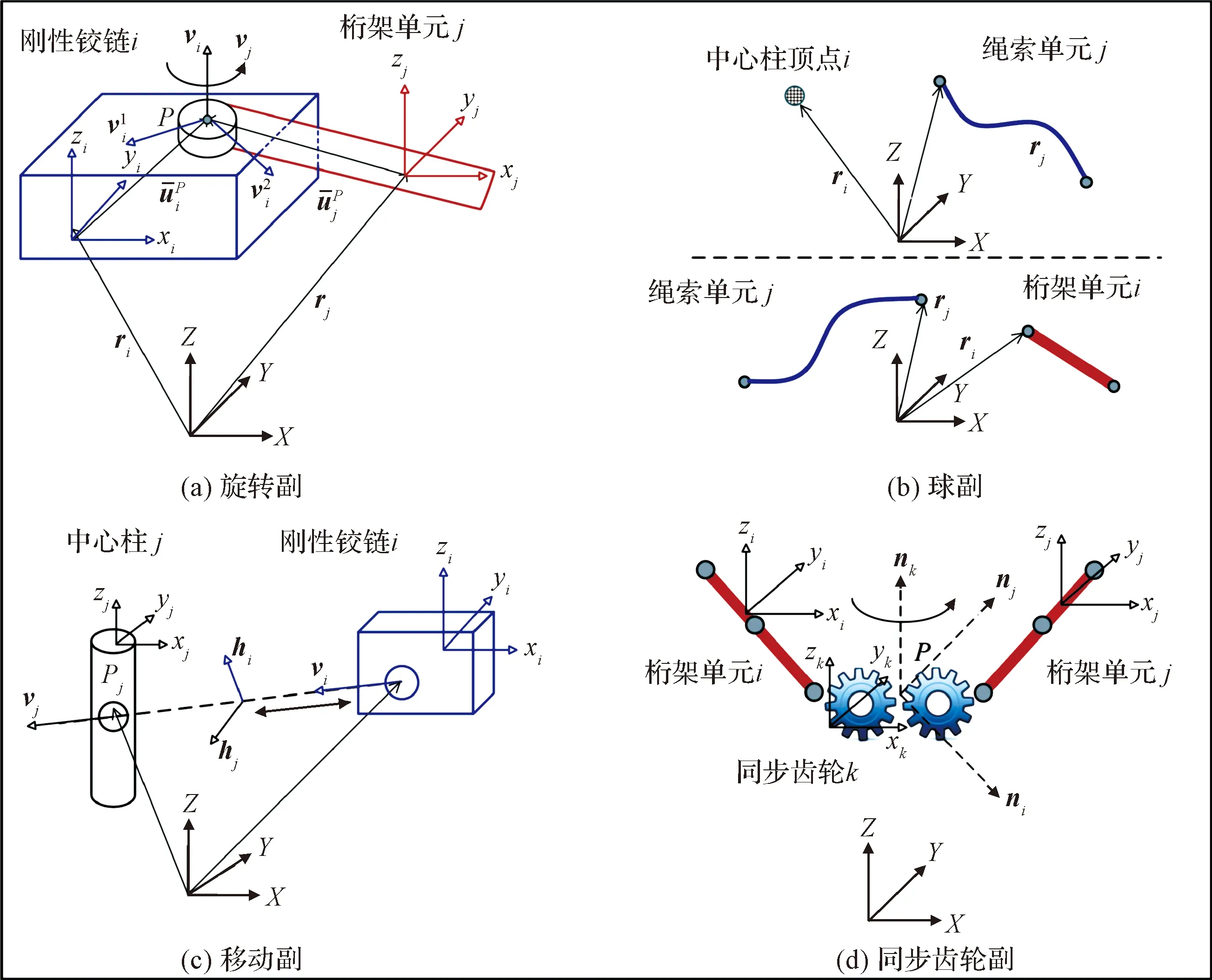
图3 环柱式天线中约束副形式Fig.3 Constraint pairs in a rod-cable antenna

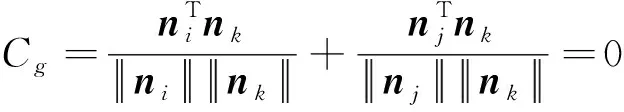
(13)

式中：=,是索长度。

1.5 模型校验

在环柱式天线展开过程中，绳索需带有一定大小的张紧力，其作用是维持桁架展开受力的稳定性，本小节采用多体动力学商业软件MSC.ADAMS对本文模型进行校验，其中上下斜拉索通过ADAMS软件中FE part柔性体模块中的3D beam单元建立，该单元基于绝对节点坐标理论进行了一定的改进，可表征绳索大位移、大变形。模型参数见表1，结构展开时间为300 s，采用隐式积分求解，步长选择为5×10s，驱动函数如式(2)所示，主动源数量采用6个，均匀地分布在环形桁架上。

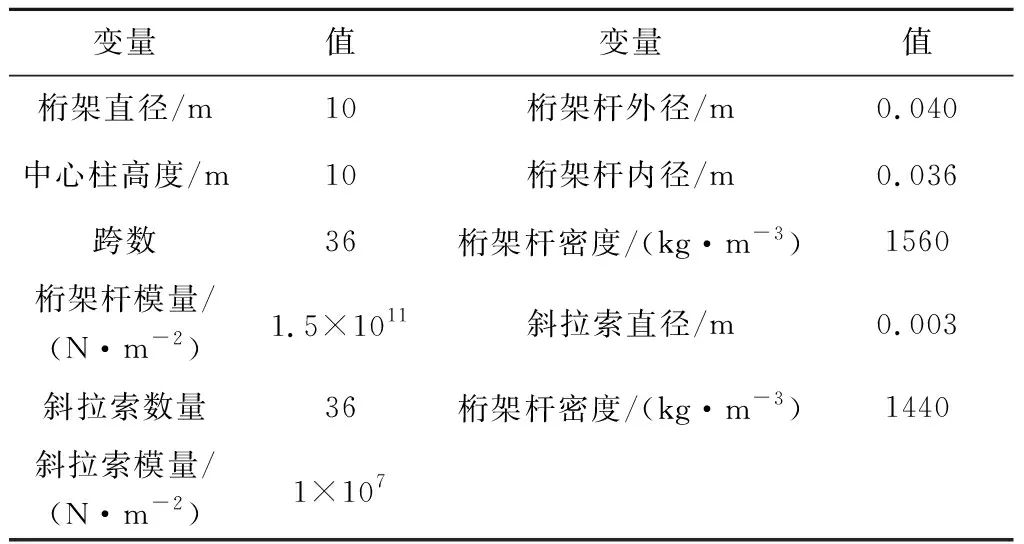
表1 环柱式天线模型参数Table 1 Parameters of the rod-cable antenna

式中：是3×3的方阵，是1×3的零阵，是3×1的零阵。另外，形函数系数为,=1,2,…,6,表达式为：

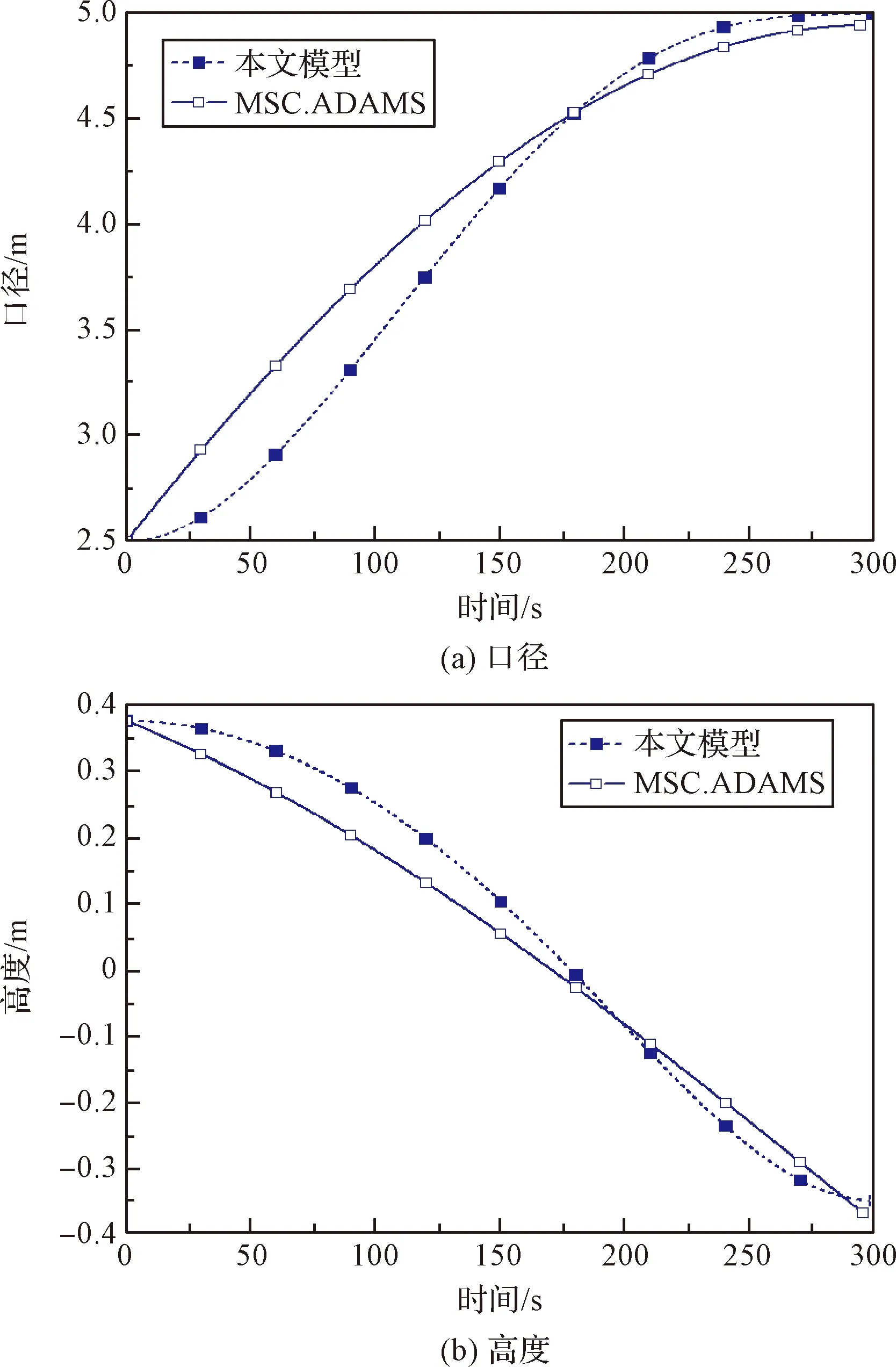
图4 桁架口径与高度变化情况Fig.4 Diameter and height change of the hoop truss

其次，与MSC.ADAMS模型计算的结果对比发现，本文模型在展开过程中出现了一定的弹性振动，这是因为本文桁架为多柔体模型，而MSC.ADAMS中的桁架为多刚体模型。桁架在受到上下斜拉索的向心作用时，其展开会呈现一定的振动效应，这也说明了本文模型能反映更加真实的桁架展开情况。

2 结构中绳索释放-桁架展开耦合动力学分析

本节研究环柱式天线展开过程中，绳索释放运动与桁架展开运动之间的耦合动力学行为，并分别探究绳索模量、绳索直径以及绳索数量对桁架展开运动的影响。

2.1 绳索模量

本小节测试绳索模量对环柱式天线展开动力学的影响，模量大小分别选择为=1×10N/m、=1×10N/m以及=1×10N/m，除模量外的其他参数保持表1中的数值大小。

图5所示为桁架驱动力矩变化情况。可以发现，当绳索模量越大时，对桁架驱动力矩的要求也越高。从图5的小图中发现，对比成功展开的两组算例，即模量为=1×10N/m和=1×10N/m时，驱动力矩增加近3倍，说明绳索模量增大，对桁架的径向向心力也越大，因此桁架展开所需的力矩也随之增加。

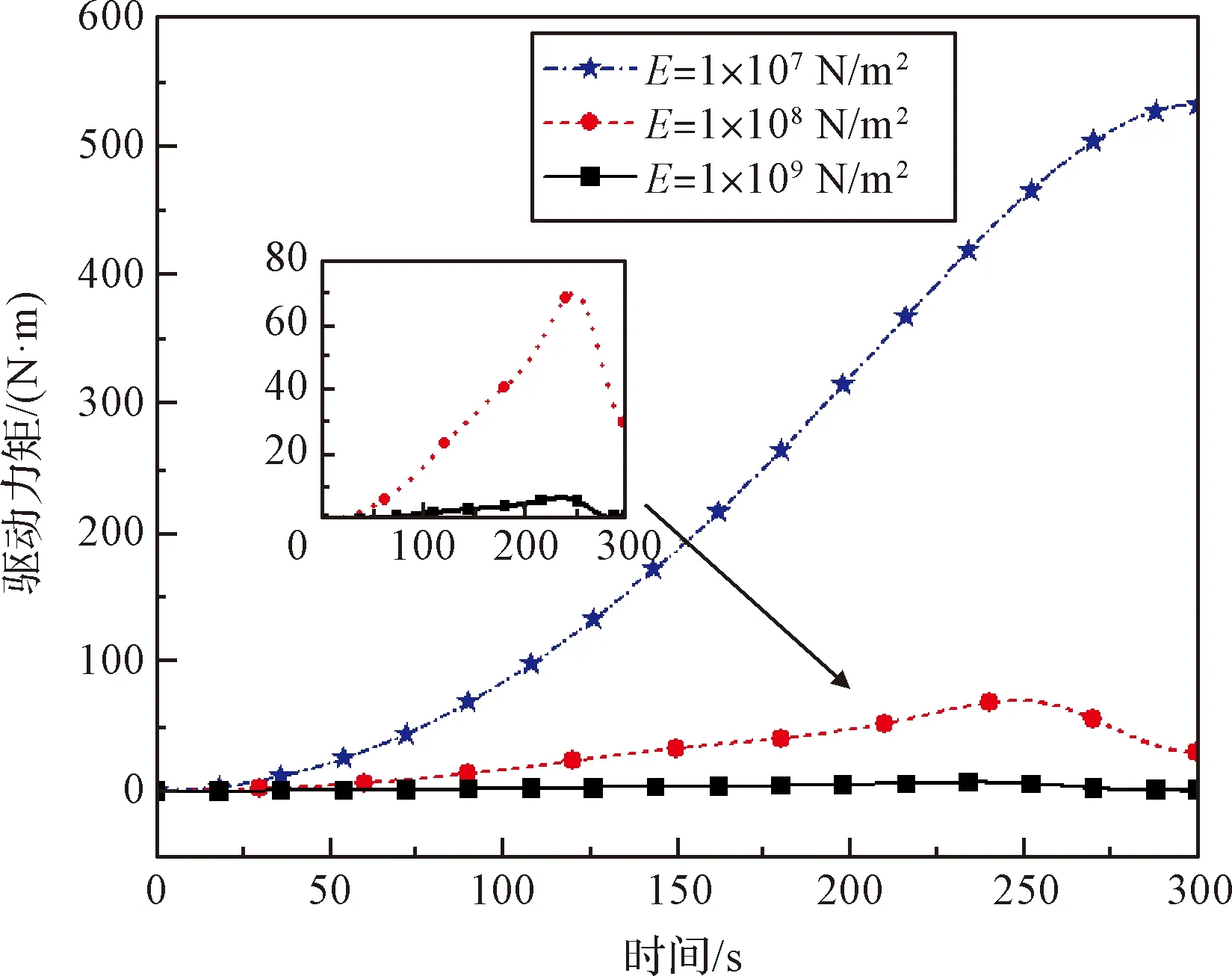
图5 桁架驱动力矩变化情况Fig.5 Driving moment change of the hoop truss

图6所示为模量=1×10N/m情况下绳索力变化情况。可以发现，与上铰链连接的绳索力大于下铰链连接的绳索力，这是因为下铰链施加了径向移动副，桁架在高度上的运动是由上铰链向下伸展至下铰链平面内。因此，这种情况中与上铰链连接的绳索长度更长，导致其受力更大。

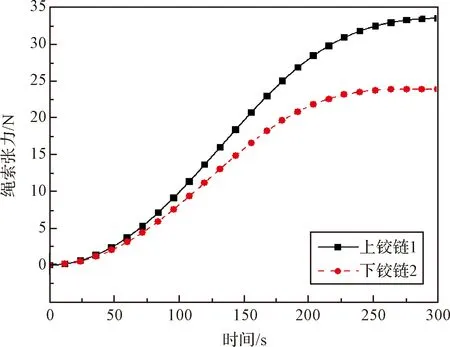
图6 绳索张力变化情况Fig.6 Change of the cable tension force

图7所示为模量=1×10N/m情况下桁架杆件的最大受力分布情况，可以得知当采用6个主动源均匀布置的方式，受力最大杆件是与主动源连接的杆件。

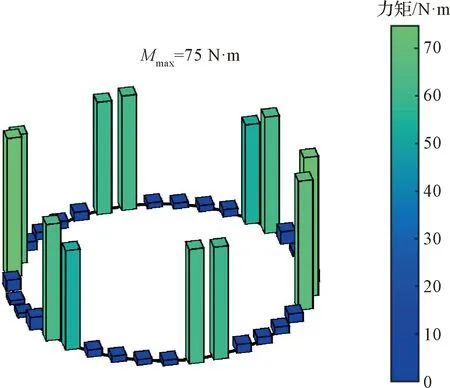
图7 桁架最大受力变化情况Fig.7 Change of the maximum moment on the hoop truss

2.2 绳索直径

本小节测试绳索直径对环柱式天线展开动力学的影响，选择直径大小进行测试，分别是=0.003 m、=0.0025 m以及=0.0035 m，除直径外的其他参数保持表1中的数值大小。

图8和图9分别为绳索力和桁架最大受力的变化情况。可以发现，绳索直径增大导致绳索力上升，这种情况下将造成桁架的受力也增大，所需的桁架驱动力矩也随之增大，可能造成桁架杆件的断裂，不利于桁架的顺利展开。

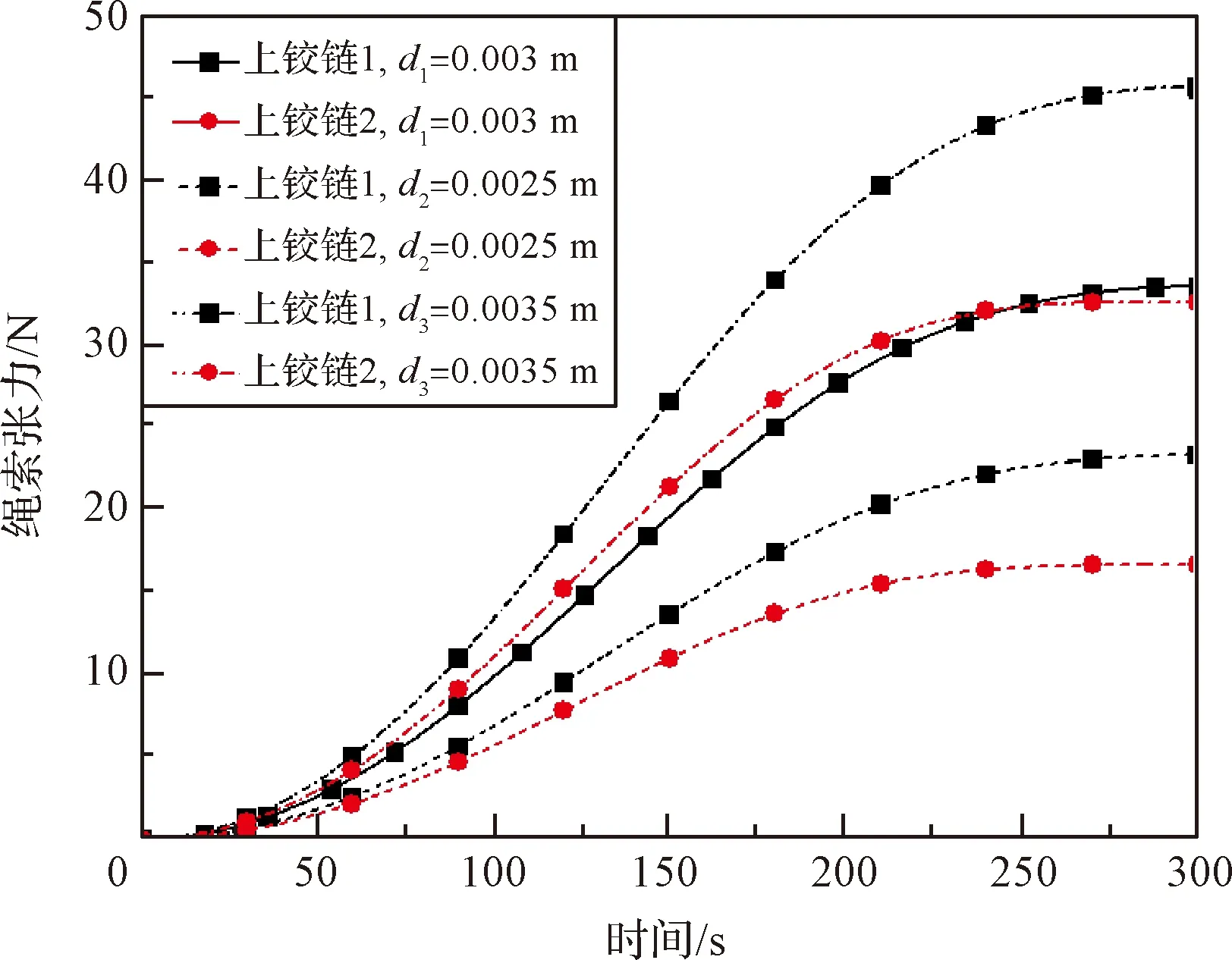
图8 绳索受力变化情况Fig.8 Change of the cable tension force

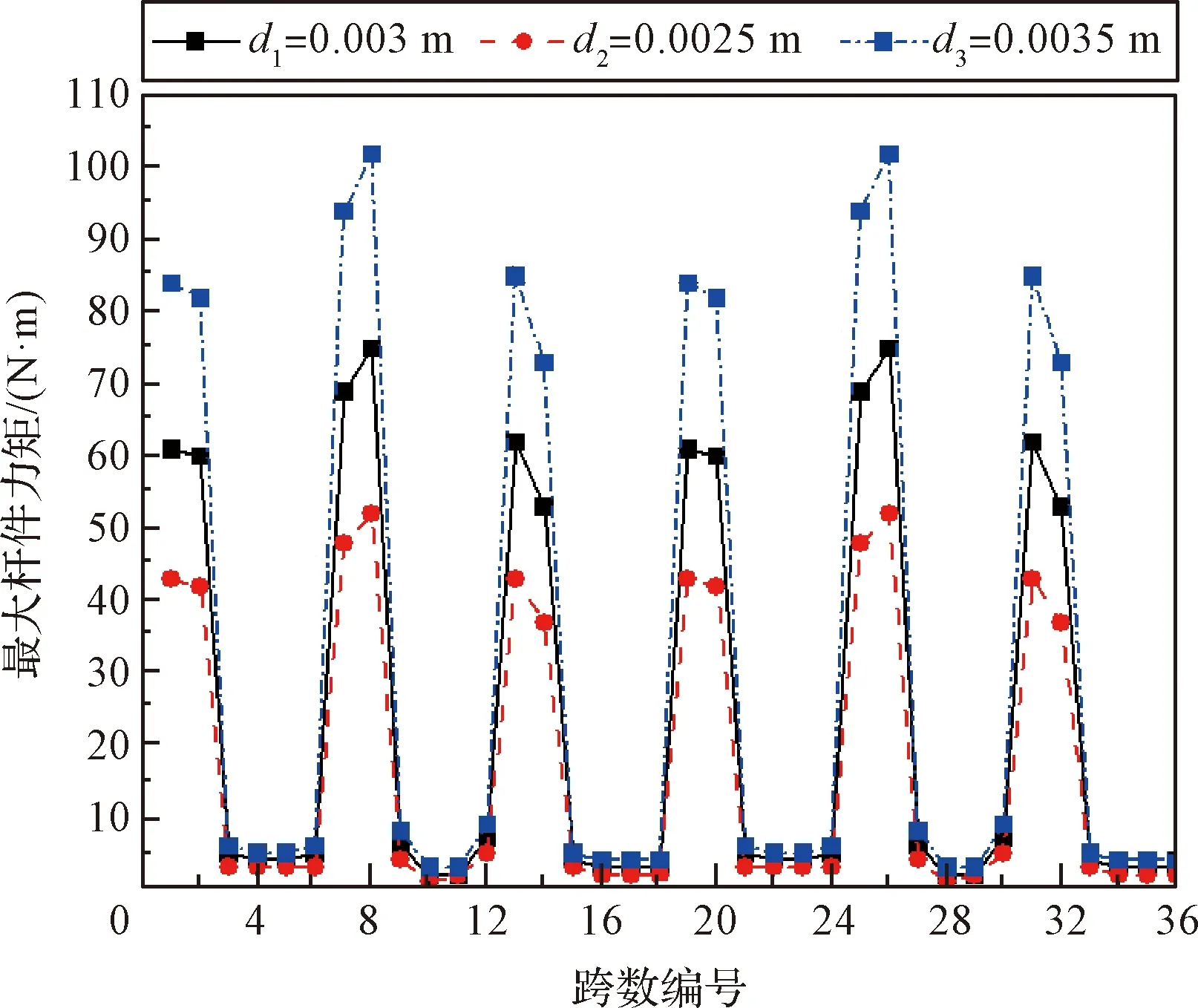
图9 桁架受力变化情况Fig.9 Change of the moment on the hoop truss

2.3 绳索数量

本小节测试绳索数量对环柱式天线展开动力学的影响，分别选择单绳索(每个铰链仅连接1根绳索，总共36根)和双绳索(每个铰链同时连接上、下2根绳索，总共72根)情况进行测试。

图10(a)是单、双绳索情况下绳索力的变化情况。可以发现，双绳索情况下的绳索力比单绳索的绳索力大。这是因为双绳索模型中每个铰链处连接2根绳索，并且这2根绳索在展开过程中长度变化不相同，这会导致铰链在上、下平面所受绳索力不同，加之上、下2根绳索在展开过程中相互拉扯，造成了双绳索情况下绳索力的增大；而单绳索模型中每个铰链处仅连接1根绳索，使得展开过程中每个铰链仅受单根绳索力的作用，因此单绳索下绳索力变化较小。

图10(b)是双绳索情况下绳索力的变化情况。铰链1位于桁架上平面，铰链2位于桁架下平面。由于桁架下平面铰链施加了径向移动副，被约束住了高度上的运动，因此桁架的展开是从上平面向下平面伸展，导致了铰链1上绳索力大于铰链2上绳索力。

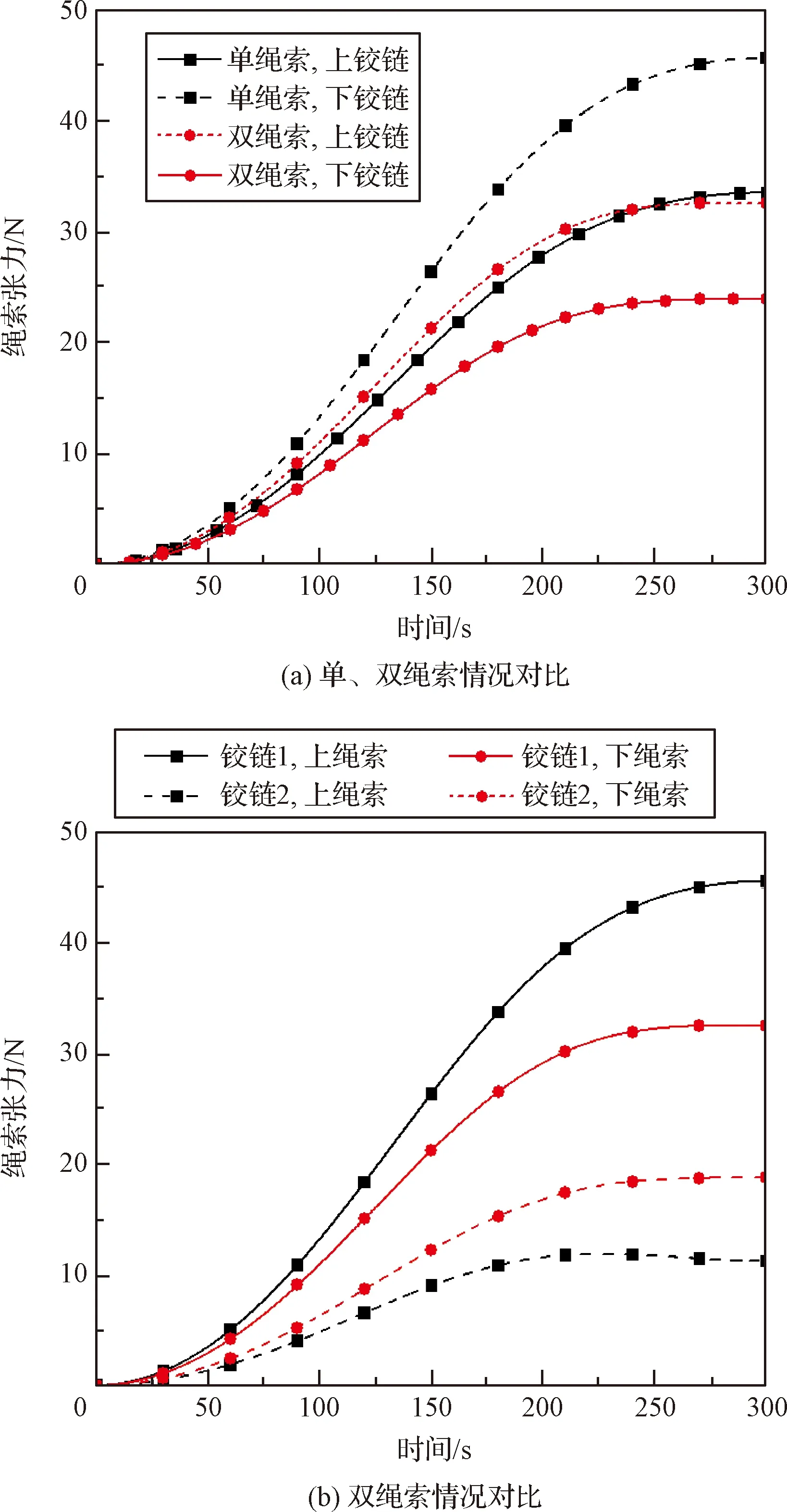
图10 绳索力变化情况Fig.10 Change of the cable force

图11分别为桁架最大受力变化情况。可以发现: 1) 绳索数量增大导致桁架的受力也增大，双绳索下桁架杆件的最大受力几乎为单绳索情况的2倍，说明了两种绳索模型在数量上的差异(2倍的关系)体现在了杆件受力上; 2) 双绳索中铰链同时受到上、下两根绳索的作用力，导致铰链处的受力矩不均，使得双绳索下杆件所受力矩较大。

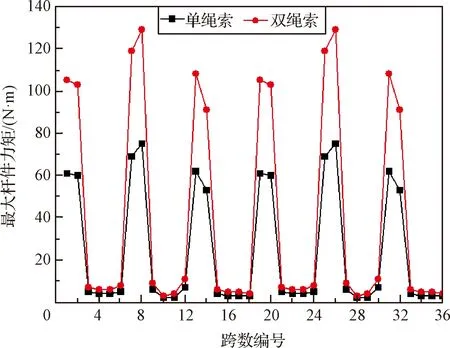
图11 桁架受力变化情况Fig.11 Change of the moment on the hoop truss

3 环柱式天线展开过程的能量分析

环柱式天线的桁架展开过程是将桁架的收拢构形转变到展开构形。从能量角度分析，电机输入动能转化成环形桁架和斜拉索的弹性势能。图12和图13分别为绳索和桁架弹性势能的变化情况，本算例中的绳索弹性模量选择=1×10N/m。可以发现：1) 绳索的弹性模量(=1×10N/m)比桁架的模量(=1×10N/m)小4个数量级，导致绳索柔性特点显著，弹性势能较大；2) 对比单、双绳索情况，绳索数量的差异造成弹性势能量级差异几乎为2倍的关系；3) 绳索越粗，弹性势能越大；4) 由于绳索一直被拉伸，因此它的弹性势能变化趋势一直增大。从环形桁架的弹性势能变化趋势中可以发现，桁架变形最大的时刻处于展开中间阶段。

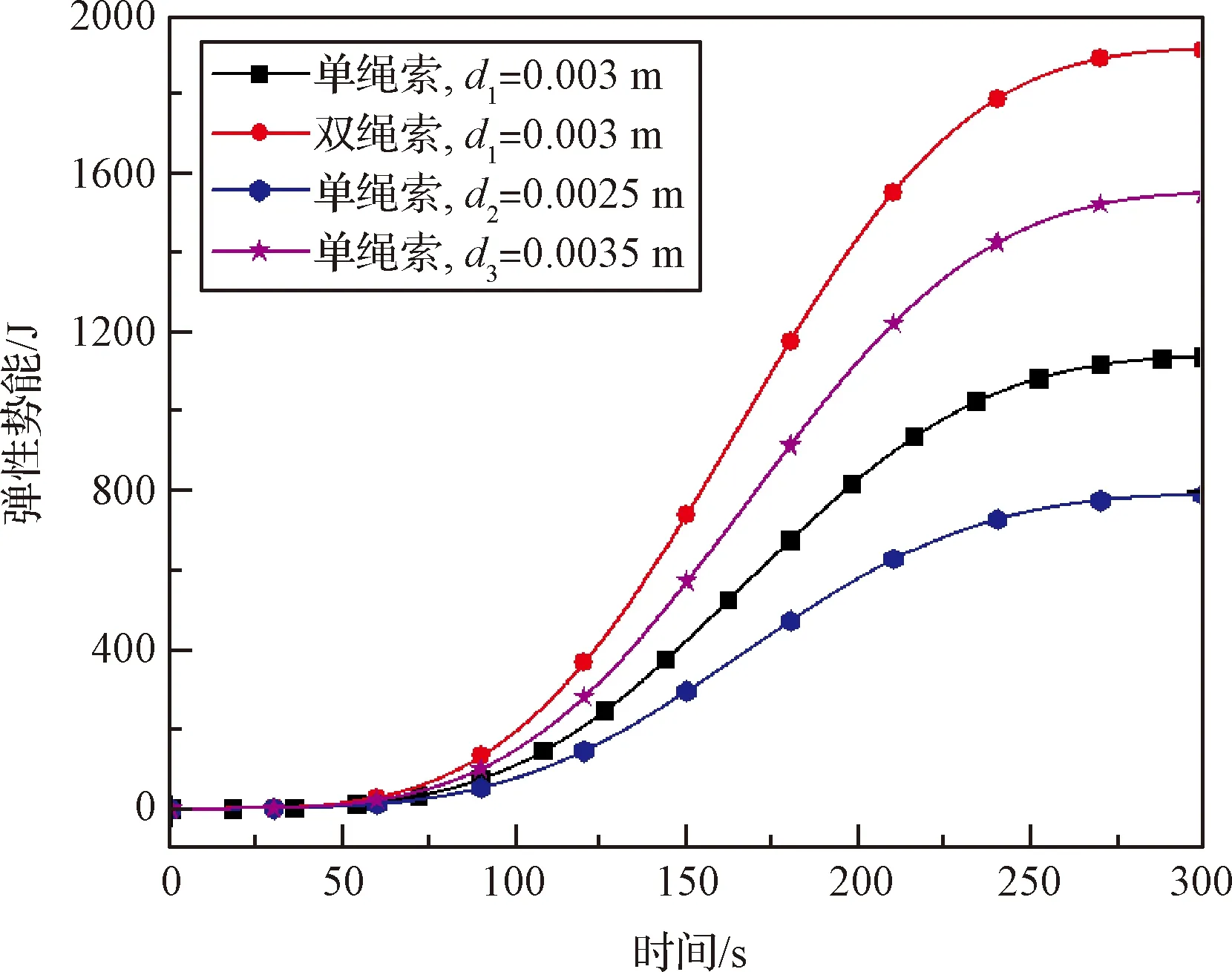
图12 绳索弹性势能变化情况Fig.12 Change of the elastic energy of the cables

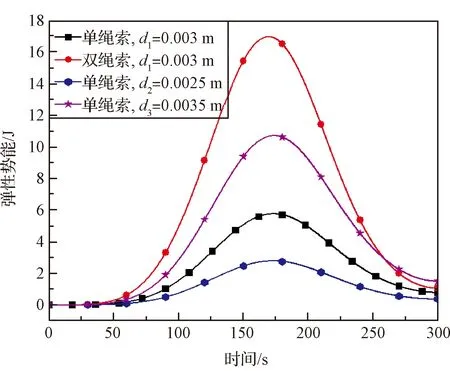
图13 桁架弹性势能变化情况Fig.13 Change of the elastic energy of the hoop truss

4 结 论

本文采用多柔体动力学方法建立了带绳索结构的环柱式天线多体系统模型，实现了结构中绳索释放与桁架展开间的耦合动力学分析，并通过与商业软件MSC.ADAMS仿真结果比对，校验了该模型的有效性。得到以下主要结论：

1)绳索弹性模量提升1个数量级，导致桁架的驱动力矩增加近3倍；另外，绳索直径增大1 mm，导致桁架和绳索受力增大近1倍。

2)单绳索下的绳索力较小，桁架杆件受力和桁架驱动力矩较小，这是因为单绳索中每个铰链受力矩均衡，仅受单根绳索的作用力;而在双绳索中铰链同时受到上下两根绳索的作用力，导致铰链处受力不均，使得双绳索下杆件所受力矩增大。

3)桁架展开到位时，其弹性势能降低近75%(单绳索情况)和88%(双绳索情况)，而绳索的弹性势能一直增加，说明了绳索在桁架展开过程一直被张紧，提供一定的刚度，有利于维持桁架构形稳定。

综上，环柱式天线展开过程中，绳索张紧力越大对桁架的径向向心作用越明显，不利于桁架的顺利展开。因此，环柱式天线设计时可以从材料、工艺角度考虑，尽可能优化斜拉绳索的材料属性和数量，并一定程度地提高桁架杆件刚度，从而减少绳索和桁架的受力。