火箭返回制导动力着陆段的自适应启动方法

袁 晗，王小军，牟 宇，张宏剑，张普卓

(1. 北京宇航系统工程研究所，北京 100076；2. 中国运载火箭技术研究院，北京 100076)

0 引 言

航天运载器的重复使用具有降低发射成本、解决落区安全的重要意义，2015年以来美国的私营航天公司SpaceX和Blue Origin已经通过垂直起降的方式成功实现火箭一子级回收和重复使用，验证了垂直起降重复使用火箭(简称垂直起降火箭)在目前的技术水平下是一种技术上可行、经济上合理的运载器重复使用方案。设计垂直起降火箭返回的制导控制方案时，通常将飞行过程划分为多个阶段分别进行设计。以不返回发射场的任务为例，其返回飞行剖面如图1所示，各阶段分别为：调姿滑行段AB、动力减速段BC、气动减速段CD和动力着陆段DE等。其中，动力着陆段具有初始状态偏差大、着陆精度要求高，且燃料消耗受制导方法影响大等特点，近年来诸多学者对动力着陆制导开展了大量的研究，通常基于在线轨迹规划，通过间接法或直接法等轨迹规划方法在线生成当前状态对应的最优轨迹，从而获得制导指令输出。为降低重复使用带来的火箭运载能力损失，制导方法中通常以燃料最优作为优化目标。燃料消耗不仅受制导方法影响，还与动力着陆段的初始状态有较大关系，不合理的启动点将增加燃料消耗，甚至导致启动点的状态在动力着陆可行域之外。目前，部分研究通过单一状态量触发方法在线确定动力着陆段的启动点，如时序触发、高度触发等。然而，初始状态偏差较大时，上述方法难以保证启动点为燃料最优，且存在启动点接近可行域边界，甚至在可行域之外的风险。

图1 典型垂直起降火箭飞行剖面Fig.1 Typical flight profile of vertical-takeoff-vertical-landing rockets

为解决单一状态量触发方法的不足，众多学者对动力着陆段自适应启动方法进行了研究。针对火星着陆问题，Lu等提出软着陆轨迹预测自适应启动方法，该方法通过在线预测软着陆轨迹的航程判断是否启动发动机并启动动力着陆段(简称启动发动机)，软着陆轨迹为仅施加终端高度和速度约束、松弛终端水平位置约束时的燃料最优轨迹。但燃料最优启动点的动力着陆轨迹并非软着陆轨迹，且二者航程存在显著差异，故该方法难以得到燃料最优启动点。Jiang等提出强化学习决策方法，离线训练决策是否启动发动机的神经网络策略函数，但神经网络策略函数的可解释性较差，导致目前工程上难以应用。针对火箭垂直回收问题，Wang等和邵楠等提出多种数值优化方法，通过对气动减速段和动力着陆段联合轨迹规划寻找燃料最优启动点，但由于在线计算效率难以满足工程要求和算法收敛性难以保证，限制了该类方法的工程应用。Song等提出中间推力轨迹自适应启动方法并通过GNC验证飞行器“Peacock”进行了实验验证，该方法通过判断火箭能否以恒定中间推力的轨迹实现着陆判断是否启动发动机，可使启动点具有较高的鲁棒性，但难以保证启动点的燃料最优性。

针对气动减速段中在线判断燃料最优启动点的问题，本文对火箭垂直返回中的燃料最优启动点进行了研究，采用一种解析的推力剖面和攻角剖面形式描述从燃料最优启动点出发的燃料最优动力着陆轨迹(简称最优启动点的动力着陆轨迹)。结合上述剖面形式，提出了燃料最优启动点的判断条件，进而设计了一种动力着陆段自适应启动方法。仿真结果表明，该方法得到的启动点与数值优化方法得到的燃料最优启动点十分接近。

1 火箭着陆问题描述

针对研究的气动减速段和动力着陆段的制导问题，本章将给出火箭返回的动力学模型，及气动减速制导和动力减速制导的方案。

1.1 火箭返回的动力学模型

在以目标着陆点为原点的站心直角坐标系(简称站心坐标系)研究返回过程，该坐标系的向为纵向，向为高度，向为横向。视地球为球形，忽略引力摄动。采用三自由度质点动力学模型，火箭的控制量为推力、攻角和侧滑角，假定推力方向始终沿箭体轴线。动力学方程为

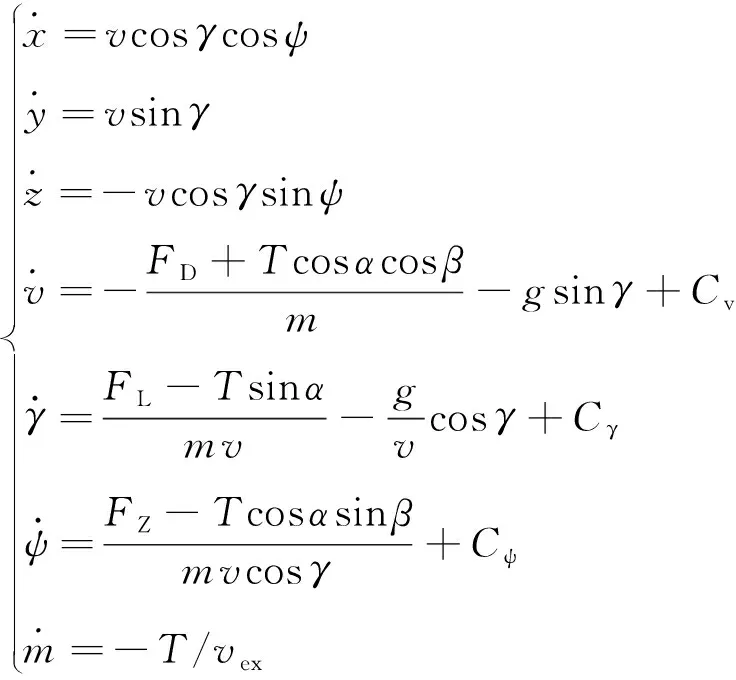
(1)

式中：为火箭的飞行速度；为速度倾角；为航迹偏航角；为火箭质量；为重力加速度；为火箭发动机比冲；,和为地球曲率、牵连加速度和Coriolis加速度在三个运动方向分别的影响，具体见文献[17]；=(+)为重力加速度，其中为目标着陆点处的重力加速度，为目标着陆点处的地心距离；,和分别为气动阻力、升力和横向力，将其表示为

(2)

式中：为动压；为阻力系数；′为升力系数导数，设为常数，升力系数()形式较为复杂难以解析表示，小攻角下可近似为()≈′，由于火箭为轴对称体，横向力系数()≈′；为大气密度，采用标准大气参数；为参考面积。

1.2 约束和优化目标

以气动减速段开始作为分析的初始状态，设该时刻为=0，动力着陆段初始时刻为，终端时刻为。记=0时刻的状态为[,,,,,,]。动力着陆段的初始状态为气动减速段的终端状态。动力着陆段的终端位置、速度、倾角固定，终端质量和航迹偏航角无约束，动力着陆段的终端约束为

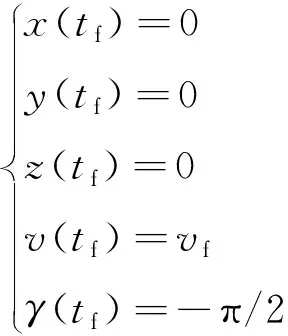
(3)

式中:≥0。以燃料最优为目标，目标方程为

min=-()

(4)

气动减速段无发动机推力，即=0。动力着陆段中发动机的最大推力、最小推力和推力调节速度均面临约束，将其简化为常值约束，分别为

≤≤

(5)

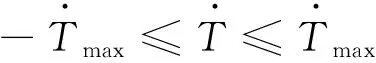
(6)

其中,>。将气动载荷、舵面配平能力等假定为攻角和侧滑角及其变化率的常值约束，为

(7)

(8)

终端时刻推力的大小无约束，由于终端时刻要求以竖直姿态触地，故终端时刻的攻角、侧滑角约束为

()=()=0

(9)

1.3 分段制导方案

火箭在气动减速段中通过该段的制导算法生成攻角、侧滑角指令，同时通过自适应启动算法自主地确定是否启动发动机。启动发动机后，进入动力着陆段，且不再执行自适应启动算法。下面给出分析动力着陆启动问题时采用的分段制导方案，其中气动减速制导用于生成定量的返回轨迹，动力着陆制导用于生成动力着陆轨迹，进而给出启动点的可行性和燃料消耗。

气动减速制导采用文献[17]的预测制导并进行改进。文献[17]给定虚拟目标点在站心坐标系中坐标为[,,]，通过参数和确定预测轨迹的攻角剖面和侧滑角剖面，利用对动力学方程式(1)积分预测=时的水平位置坐标|=,|=，进而以|==,|==为条件求解和。文献[17]中设定攻角、侧滑角为时间的线性函数，由于飞行时间受初始状态和攻角、侧滑角剖面影响较大，该方法限制了水平机动能力。因此不同于文献[17]，本文设定攻角和侧滑角指令为高度的函数。预测落点坐标时，式(1)中推力取0，攻角和侧滑角与和的关系分别为

=min{max{(-)|-|,0},}

(10)

=min{max{(-)|-|,0},}

(11)

式中:,为预先给定的参数，即<时指令为0，<时指令为0，取=1 km,=5 km。

本文提出的自适应启动方法不依赖于具体的动力着陆制导算法，采用数值轨迹优化方法直接得到从启动点出发的燃料最优动力着陆轨迹来评价启动点的可行性和燃料消耗，避免了不同制导算法对启动点的可行性和燃料消耗评价结果的影响。轨迹优化采用GPOPS算法，动力学模型为式(1)，终端约束为式(3)，优化目标为式(4)。

2 燃料最优启动点的性质分析

在纵向平面(--平面)分析典型返回轨迹中使动力着陆段燃料消耗最小的启动点(即燃料最优启动点，简称最优启动点)，及对应的动力着陆轨迹的性质。为便于得到控制量剖面的规律，文中忽略推力变化率约束(6)、攻角变化率约束(8)，终端状态约束(3)中忽略倾角约束，仅考虑如下终端约束：()=0,()=0,()=,()=0。但在仿真校验中考虑了上述忽略的约束，验证了依据本章结论提出的算法仍有效。

采用如表1所示的火箭参数和初始状态，通过如下方式生成多条气动减速段轨迹：初始状态相同，通过为气动减速段的预测制导选取不同虚拟目标点生成不同轨迹，令虚拟目标点的高度均为=0。由于气动减速制导采用无动力轨迹预测落点，无动力轨迹航程大于动力着陆航程，故虚拟目标点应在目标着陆点前方。数值仿真表明<786m时气动减速段不存在动力着陆可行解，故取分别为100 m，150 m，…，500 m，共9条轨迹。采用GPOPS计算从气动减速轨迹的不同时刻启动对应的燃料消耗，采用启动点的高度代表该启动点，得燃料消耗与启动高度曲线如图2所示，图中每条曲线下方为该曲线对应取值，由左至右依次对应为100 m，150 m，…，500 m的轨迹。

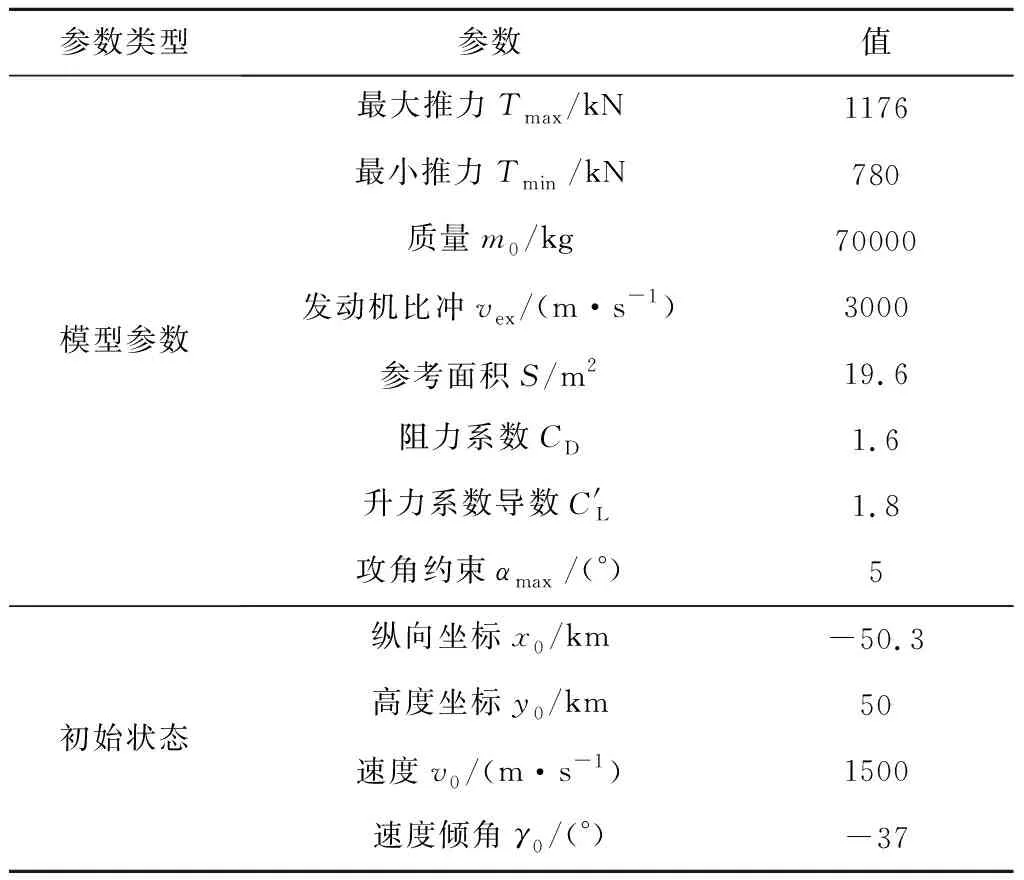
表1 火箭参数和初始状态Table 1 Rocket parameters and initial states

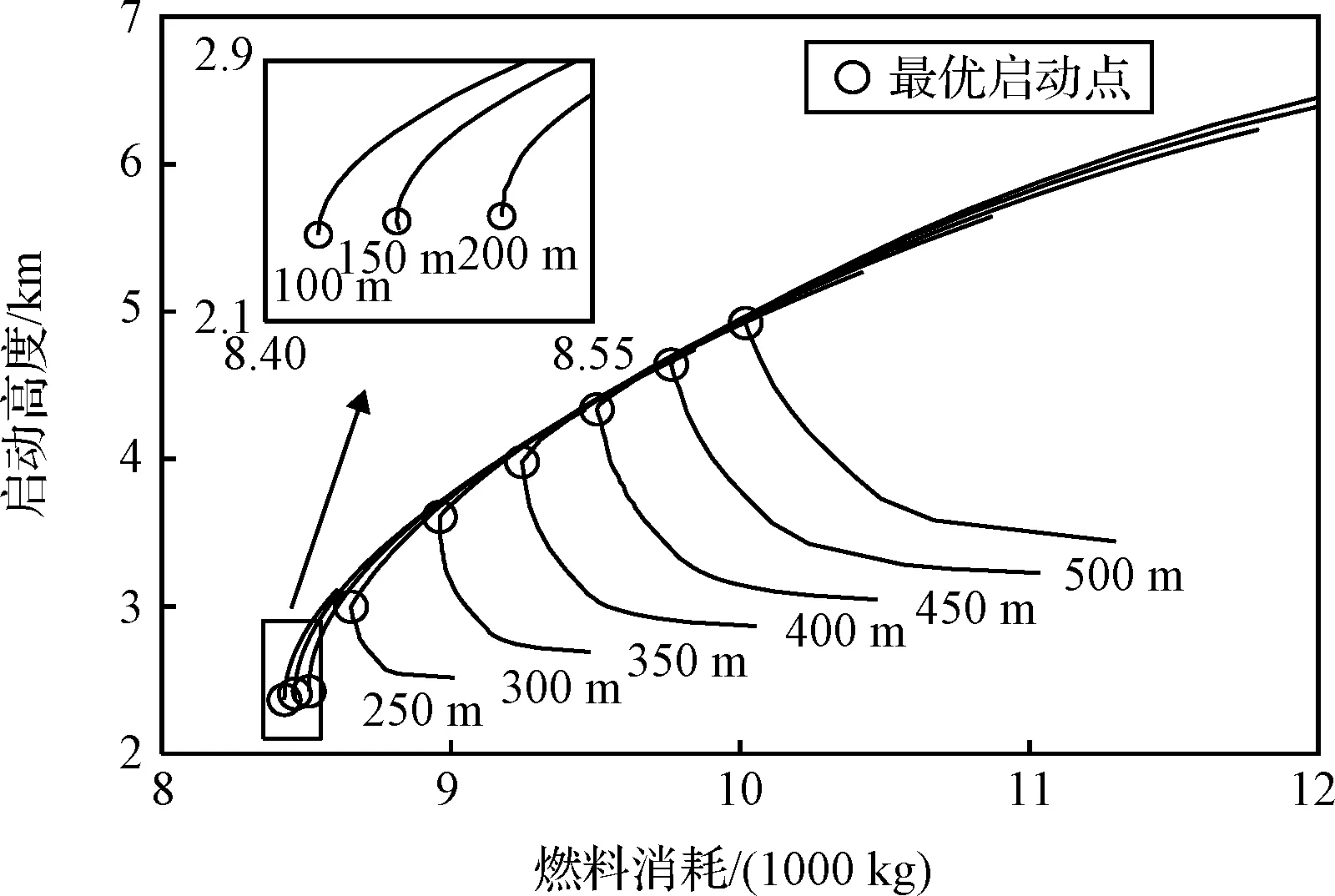
图2 不同虚拟目标点下燃料消耗与启动点关系图Fig.2 Relation between fuel consumption and starting points under different virtual target points

由图2可见，最优启动点存在位于和不位于最小可行高度两种情况：若位于最小可行高度，返回轨迹中随启动高度降低燃料消耗单调降低，如图2中为100 m至200 m的3条轨迹；若不位于最小可行高度，返回轨迹中随高度降低燃料消耗先降低后上升，如图2中为250 m至500 m的6条轨迹。以分别为200 m，300 m和400 m的三条轨迹(图2中三条加粗黑线)为例分析最优启动点的动力着陆轨迹。上述三个典型返回轨迹的最优启动点的状态及轨迹的最大、最小可行启动高度总结如表2。三个最优启动点的动力着陆轨迹的推力和攻角剖面如图3所示，图中时间零点为动力着陆段开始时刻。

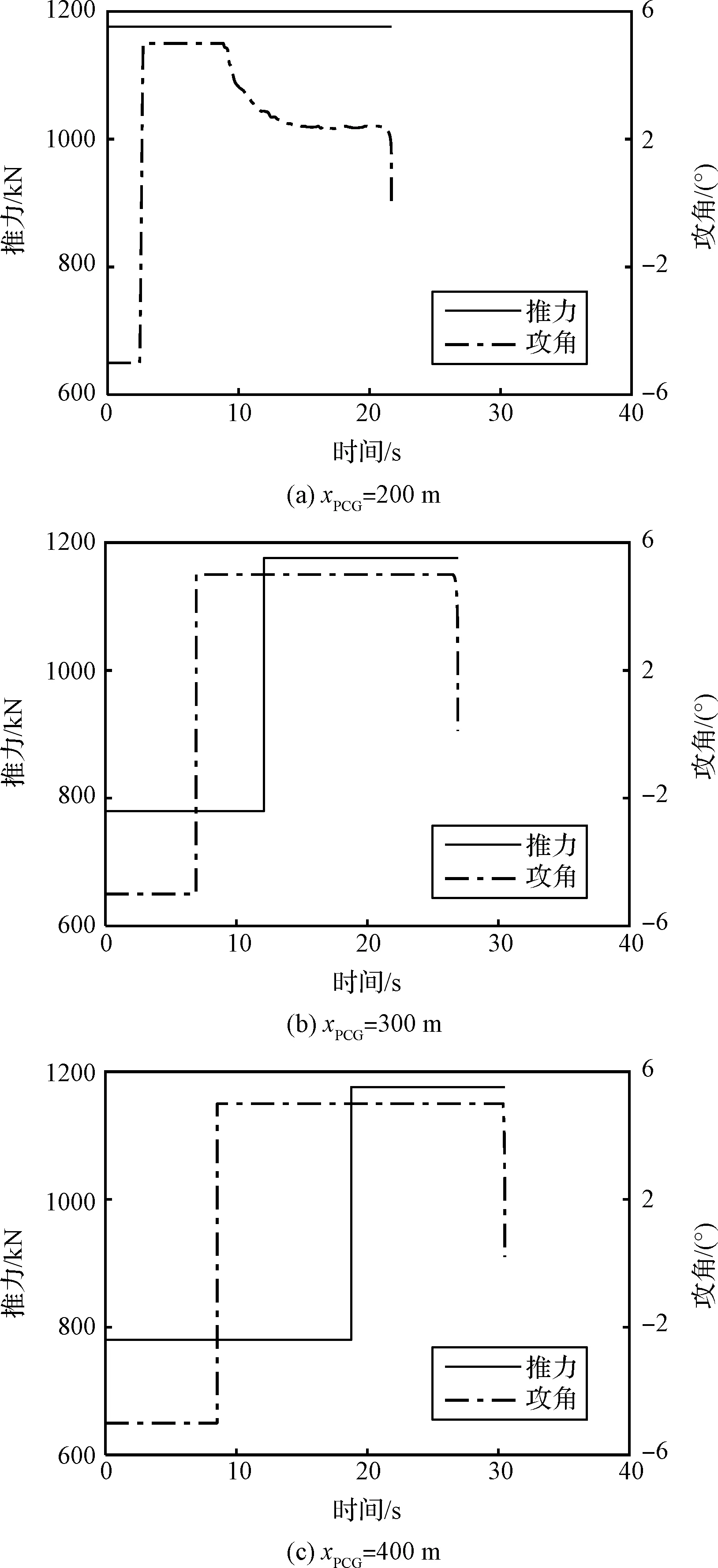
图3 燃料最优启动点的动力着陆轨迹的控制量Fig.3 Control profiles of dynamic landing trajectory of fuel-optimal handover states

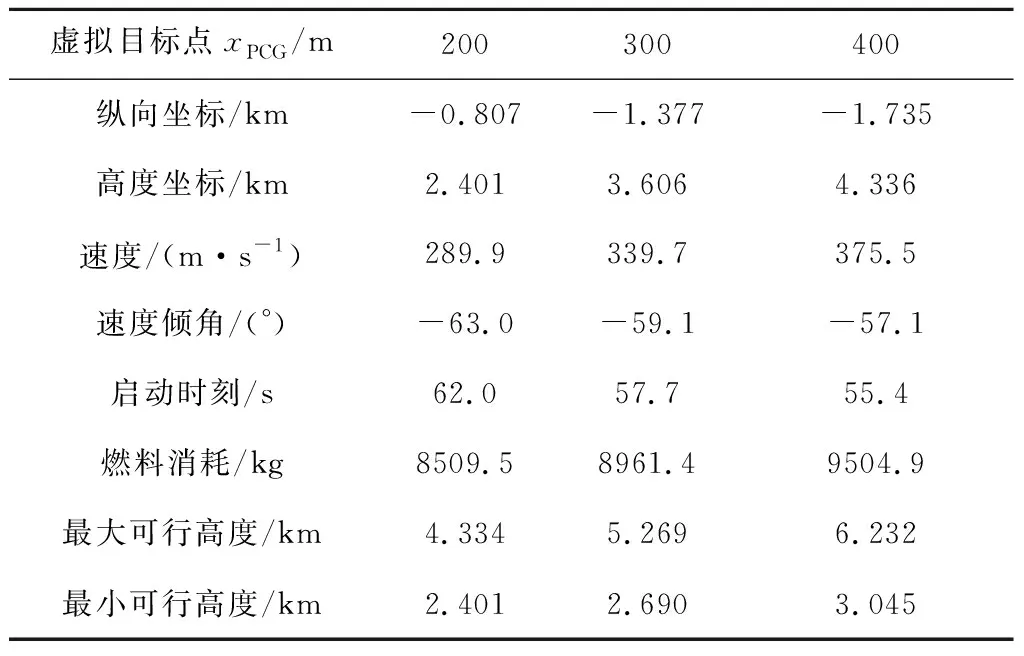
表2 燃料最优启动点的状态Table 2 The fuel-optimal powered descent initiation states

可见为200 m时，最优启动点的动力着陆轨迹的推力恒为，攻角剖面的形式较为复杂，为100 m和150 m的轨迹中上述性质均成立。为300 m和400 m时，推力剖面为-形式的Bang-Bang控制，即推力由切换至且仅有一次切换，令为推力切换时刻，推力剖面表示为

(12)

为300 m和400 m的轨迹中，攻角剖面近似为Bang-Bang控制，除触地前较短时间外，攻角取值均为或-，触地前为满足终端攻角约束，攻角降至0。其他4条最优启动点不在最小可行高度处的轨迹中该性质均成立，由于此时最优启动点无法通过寻找最小可行启动高度确定，故下面重点分析为300 m和400 m的轨迹中的性质。

进一步，采用最优控制方法研究攻角正负取值与状态量的关系。仅考虑纵向平面内的运动，且忽略地球曲率、牵连加速度和Coriolis加速度影响项,和。考虑攻角较小，引入近似sin≈。将气动力式(2)代入动力学方程(1)，得动力学方程为

(13)

式(13)对应的哈密尔顿函数为

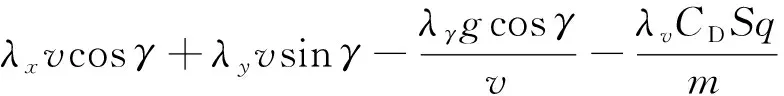
(14)

推力约束和攻角约束分别如式(5)和式(7)第一式。对上述最优控制问题，有定理1如下

设动力着陆问题的最优控制为(,)，则必满足(′-)≤0。

由极小值原理可知(,)使取极小值，将式(14)所示的记为(,)。采用反证法，设(′-)>0，则(,)-(,-)=2(′-)>0，即(,)>(,-)。由于满足攻角约束式(7)，则-必满足攻角约束，则(,-)为满足控制约束的解，则(,)未使取极小值，与“(,)为最优控制”矛盾。

数值实验表明为300 m和400 m的轨迹中最优启动点的动力着陆轨迹中恒有≥0，则由定理1得(′-)≤0。最优启动点不在最小可行高度时，对应的动力着陆轨迹的攻角剖面近似为Bang-Bang控制，仅在触地前较短时间内攻角降至0。由于攻角由降至0的过程距离触地的时间较短，此时攻角变化对轨迹影响较小，将动力着陆轨迹中取值均近似为或-，则攻角剖面表示为

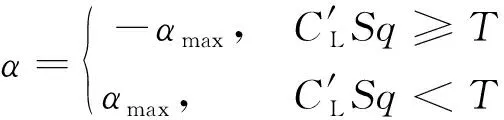
(15)

攻角与升力、推力的关系如图4所示，图中垂直于速度方向，虚线表示升力，及推力在速度方向的分量，实线表示垂直于方向的力的合力。

图4 攻角与状态量关系Fig.4 Relation between angle of attack and states

本章通过数值优化方法分析了返回轨迹中最优启动点的性质。分析表明最优启动点的动力着陆轨迹具有两种情况，第一种情况为最优启动点的高度为该条轨迹的最小可行高度，此时推力恒为，攻角剖面较为复杂；第二种情况为最优启动高度不在最小可行高度，此时推力剖面如式(12)，攻角剖面近似如式(15)。此时推力剖面中推力切换时刻为待定参数，攻角剖面与状态量的关系完全确定。

3 燃料最优自适应启动方法

3.1 基本原理

本文提出的自适应启动方法通过上述最优启动点的动力着陆轨迹的推力和攻角剖面的性质，在线判断当前状态是否在最优启动点，进而决定是否启动发动机。判断方法为：假设当前状态在最优启动点，则存在推力切换时刻，使得以当前状态为初始状态、推力满足式(12)，攻角满足式(15)、侧滑角为0的动力着陆轨迹，同时满足第2章分析中考虑的3个终端约束()=0、()=0、()=。考虑该轨迹的终端时刻自由，即具有两个未知数和，故松弛1个终端约束，通过2个终端约束确定、，此时动力着陆轨迹唯一确定，若该轨迹满足松弛的约束，代表当前状态在最优启动点。本文松弛约束()=0，通过()=0、()=两个约束确定、进而确定上述动力着陆轨迹，若该轨迹满足()近似为0，则启动发动机。本文将推力和攻角满足式(12)和式(15)，满足约束()=0、()=的轨迹称为“触发轨迹”。

火箭返回中，在气动减速段的每个制导周期通过触发轨迹的()是否接近于0判断当前状态是否在最优启动点。由于气动减速段火箭自高到低飞行，若最优启动点不在最小可行高度处，且最优启动点的高度小于初始判断时的高度，则该方法可寻找到最优启动点。本研究发现，若返回轨迹中水平速度较大，则()随启动高度降低而前移。若上一周期()<0且本周期()>0，代表最优启动点在该周期内，故将()>0作为启动条件，第一次判断得()>0时启动发动机。

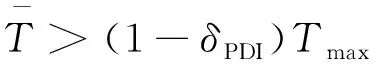
本文方法采用的触发轨迹的推力和攻角剖面与纵向平面内最优启动点的动力着陆轨迹相同，故在最优启动点处触发轨迹的航程与待飞航程相同，避免了文献[4]和文献[6]中由于触发轨迹与最优启动点的动力着陆轨迹航程存在差异，导致的难以找到最优启动点问题。此外，本方法不依赖于各飞行阶段具体的制导方法，仅需要动力着陆段采用燃料最优制导。3.2节将给出上述自适应启动算法的细节。

3.2 算法细节

首先给出触发轨迹的计算方法。由于触发轨迹的初始状态、攻角与状态的关系均已给定，触发轨迹由推力切换时刻唯一确定，推力切换时刻可通过触发轨迹的终端约束()=0、()=求解。令代表满足上述约束的推力切换时刻，s,代表任意的推力切换时刻。则对任意给定s,，将推力剖面式(12)、攻角剖面式(15)代入动力学方程式(1)进行数值积分，得速度降为时的高度|=。然后，通过Newton-Raphson法迭代求解使得|==0，从而确定触发轨迹，并令()代表触发轨迹的终端位置。求解s,对应的|=时，由于终端时刻自由，终端条件为=，因此推力切换至后以速度为自变量进行积分。从而将通过()=0、()=求解两个未知变量,的问题，转化为通过|==0求解单个未知变量的问题，提高了求解效率。

图5 整合制导方案及自适应PDI方法流程图Fig.5 Flowchart of the integrated guidance framework and the proposed adaptive PDI method

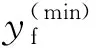
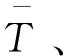
4 仿真校验

4.1 空间质点运动仿真

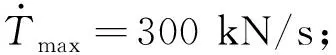
考虑三组气动减速段初始状态和三个预测制导虚拟目标点，共九条返回轨迹。初始状态以表1为标称值，并考虑初始位置、速度偏差，采用的三组初始状态如表3所示。三个虚拟目标点与第2章中分析的三组典型轨迹相同，3自由度模型中三个虚拟目标点的坐标分别为[200, 0, 0]m，[300, 0, 0]m，[400, 0, 0]m，即取上述三个取值，均为0。

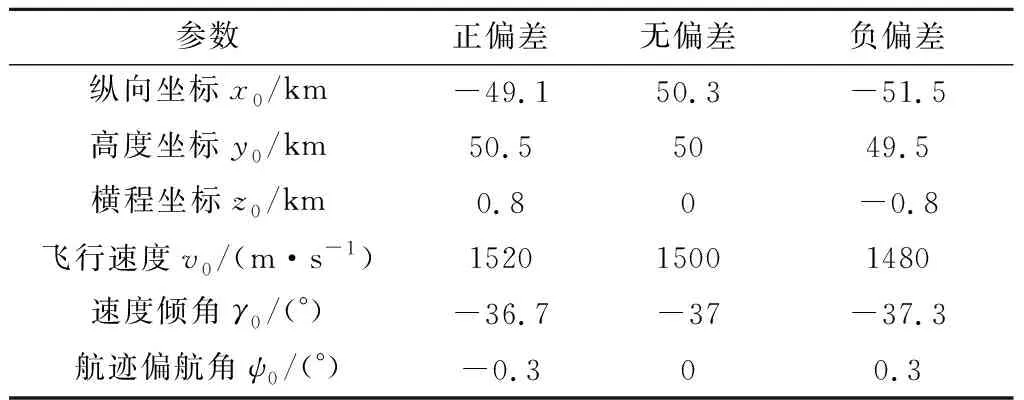
表3 气动减速段初始状态Table 3 Initial states of aerodynamic deceleration

9条返回轨迹的燃料消耗与启动点高度关系如图6所示，图中“启动点”通过提出的自适应启动方法得到。上述轨迹的启动点状态、最优启动点的燃料消耗和高度，及轨迹的最大、最小可行高度总结如表4，其中启动时刻以开始气动减速的时刻为时间零点。可见为200 m时轨迹的最优启动高度为最小可行高度；为300 m和400 m时最优启动高度均不在最小可行高度。从自适应启动方法确定的启动点开始动力着陆，上述9条返回轨迹的轨迹剖面如图7所示。6条含偏差动力着陆轨迹的推力和攻角剖面如图8所示，3条无偏差轨迹的推力和攻角剖面均与与图3相近，故图8中为列出。

图6 不同初始状态下燃料消耗与启动高度关系图Fig.6 Profiles of fuel consumption with respect to PDI states under different initial states

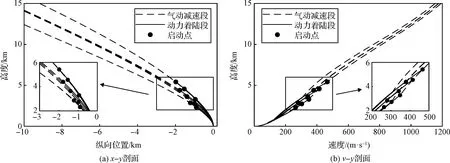
图7 典型返回轨迹的飞行剖面Fig.7 Profiles of the typical return trajectory

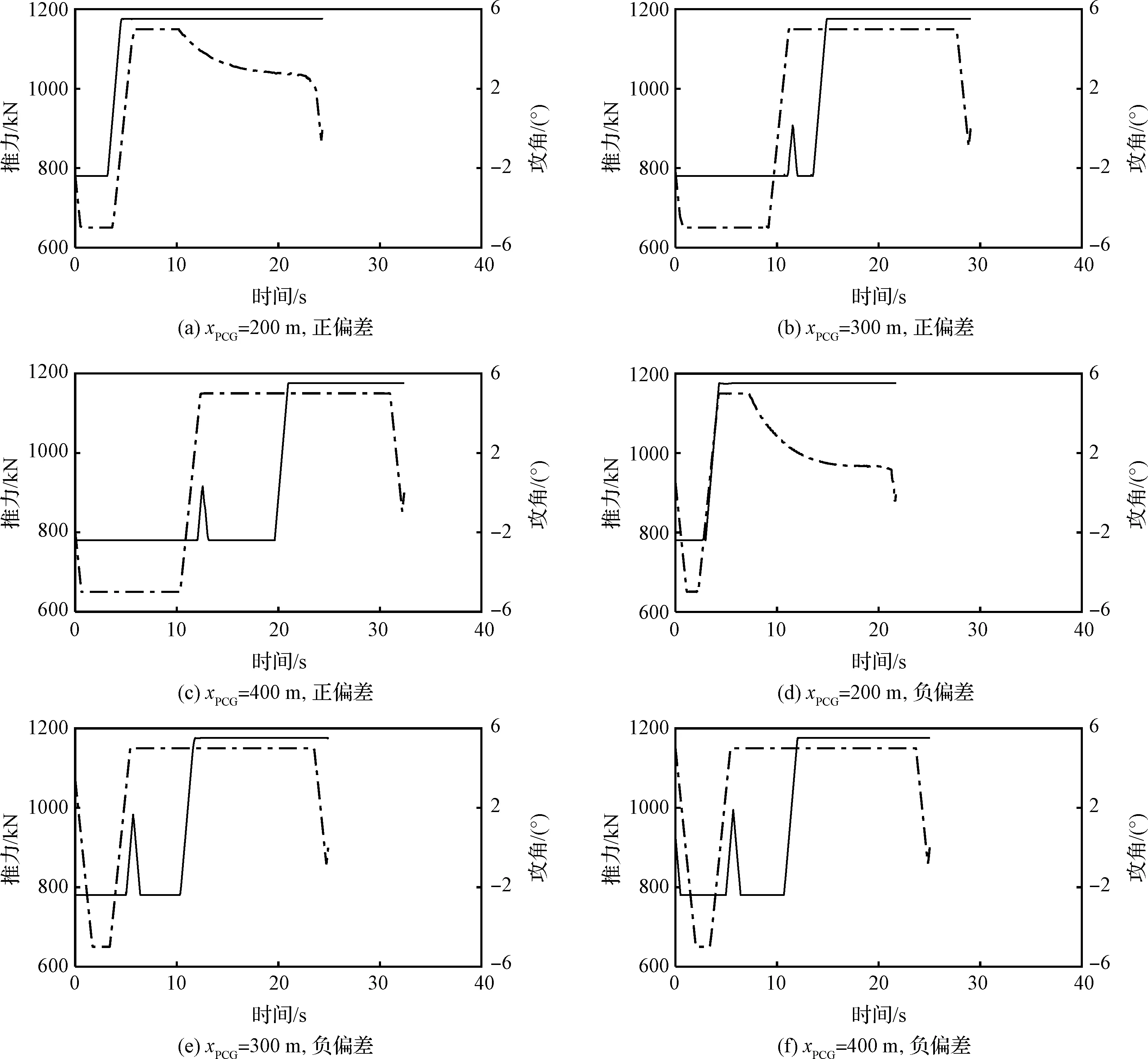
图8 典型返回轨迹启动点的燃料最优动力着陆轨迹的推力和攻角剖面Fig.8 Thethrust and angle of attack profiles of fuel-optimal powered descent trajectories of the triggered states

表4 典型轨迹的启动点状态Table 4 Powered descent initiation states of the typical cases

4.2 计算效率和收敛性

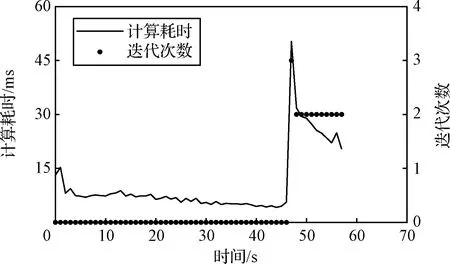
图9 自适应启动方法的计算耗时和迭代次数Fig.9 Computational time cost and iterations’ number of theproposed adaptive powered descent initiation method

可见单次求解的最大计算耗时为50.3 ms，最大迭代次数为3次，最大迭代次数出现在首次计算触发轨迹时。原因为此时的迭代初值为，随后计算中由于将上一时刻的作为迭代初值，仅需1至2次迭代即可收敛。

为直观的展示本文方法的收敛性，做迭代求解时的速度-高度剖面如图10所示，的迭代初值为-=0。初始状态为=300 m时负偏差轨迹的最优启动点的状态。图中表示第步迭代，s,表示该步中切换时刻的取值。图中第3次迭代即收敛至|==-36×10m，此时满足迭代收敛条件。

图10 触发轨迹的迭代求解Fig.10 Iterative solutions of trigger trajectories

4.3 蒙特卡洛仿真

为检验本文方法关于火箭模型参数的适应性，关于火箭模型参数、初始状态进行蒙特卡洛仿真，对比不同参数中自适应启动方法得到的启动点与燃料最优启动点间的燃料消耗的差异。考虑表5所示的9个模型参数和6个初始状态参数均在表5所示的取值范围内服从均匀分布，其中初始纵向位置为相对气动减速段零攻角、零侧滑角航程的偏差，原因为气动减速段航程受火箭参数和初始状态影响较大。火箭的侧滑角约束、侧滑角变化率约束的取值与攻角相同。气动减速段制导的虚拟目标点坐标为[300, 0, 0]m，自适应启动方法的参数与4.1节相同。

表5 火箭参数和初始状态的取值范围Table 5 Value range of the rocket parameters and initial states

进行1000次蒙特卡洛仿真，自适应启动方法所得启动点与GPOPS算法得到的燃料最优启动点间燃料消耗相对差异的统计结果如图11所示。可见尽管火箭参数和初始状态存在较大差异，但本文提出的自适应启动方法均可得到与燃料最优启动点接近的启动点。说明尽管本文方法基于特定参数下数值的结论，但在不同火箭参数中具有较好的适应性。

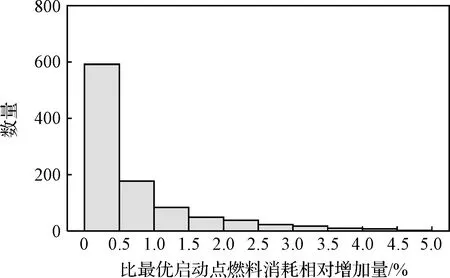
图11 比最优启动点燃料消耗相对增加量的统计结果Fig.11 Statistical results of the relative fuel usage increase for the triggered PDI states compared with the optimal PDI states

5 结 论

本文针对重复使用火箭垂直返回着陆问题，对动力着陆段的自适应启动方法展开研究，主要的工作总结如下：

1) 通过数值优化方法对返回轨迹系统分析，得到一种解析形式的推力剖面和攻角剖面，描述燃料最优启动点对应的动力着陆轨迹。

2) 设计了一种燃料最优的动力着陆段自适应启动方法。方法基于上述剖面形式判断当前是否满足燃料最优启动条件，进而实现自适应启动。

3) 对提出的自适应启动方法在多种工况下进行了数值实验，得到的启动点与燃料最优启动点十分接近，且迭代求解过程稳定，计算效率高。