绳网拖曳带帆板失效卫星的波动控制
张 扬,祁 瑞,姚傅祯
(北京理工大学宇航学院,北京 100081)
0 引 言
随着航天活动的不断进行,地球周围已经积累了大量空间碎片,这其中不乏以失效卫星为代表的大型碎片。这类碎片碰撞风险高,碰撞危害大,并且在短时间内难以自然销毁,时刻威胁着在轨航天器的运行。为应对愈发频繁的卫星发射活动,必须尽快开展针对失效卫星的主动清除工作。
在众多主动清除技术中,用系绳拖曳的方法得益于系绳质量轻、柔性强、作用距离远等优势,是目前最有希望的清除手段之一。因此,许多学者对绳系卫星系统(Tethered satellite system, TSS)的动力学特性与控制进行了研究。但对TSS的研究通常考虑单一系绳通过鱼叉、机械臂等刚性连接装置直接固连在碎片上,这可能并不适用于实际的清除情景。一方面,失效卫星往往会自旋,刚性连接装置难以直接附着,甚至可能碰撞出新的碎片。另一方面,失效卫星上一般还保留着完整的、展开的柔性附件,即使附着成功,单根系绳也难以应对拖曳过程中可能产生的附件振动断裂。面对这些实际中可能遇到的问题,一个较好的办法是将系绳末端的刚性连接装置换为柔性绳网。用绳网将失效卫星整个包裹起来,既能忽视自旋对捕获带来的影响,又能避免振动可能产生的二次碎片污染,同时还保留了系绳材料本身的优势,非常适用于失效卫星的拖曳清除情景。因此我们将系绳末端连接柔性飞网的TSS单独划分出来,并将其称为绳网组合卫星系统(Tethered-net satellite system, TNSS),如图1所示。
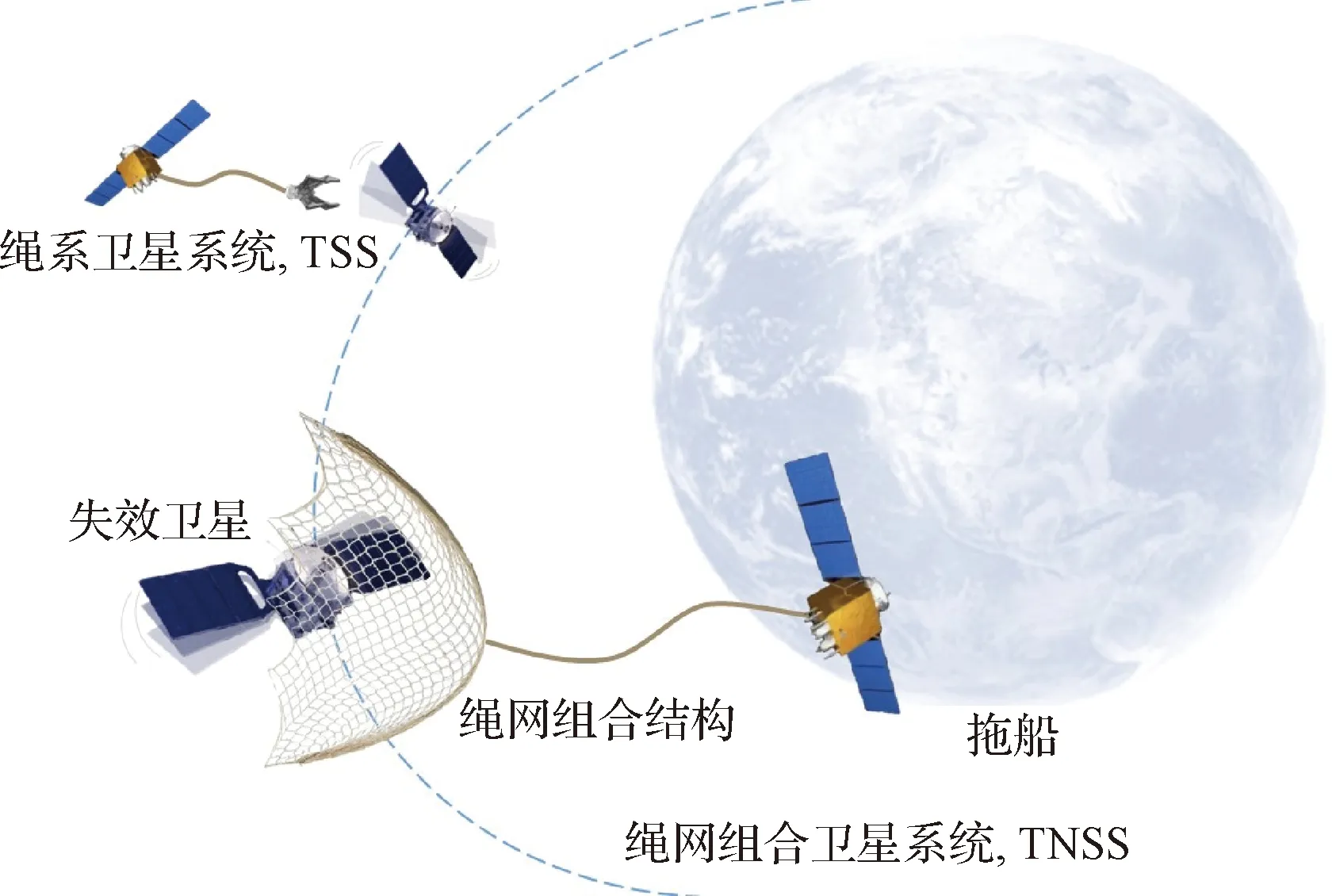
图1 TSS与TNSS示意图Fig.1 Schematic diagram of TSS and TNSS
为保证拖曳过程的安全可靠,系统的姿态稳定控制与振动抑制至关重要。尽管目前已经有许多研究从不同角度提出了基于TSS模型的拖曳控制方法,包括:调节拖船推力、调整拖船姿态、调节系绳张力、移动附着点位置、综合多种手段协同控制等。但精细绳网的加入增加了控制难度,使得这些方法并不能直接适用于TNSS模型。绳网增加了系统的柔性和复杂程度,使其更容易产生振动也更难受控。并且,基于单绳拖曳模型的控制研究大多不考虑碎片上的柔性附件,这意味着忽略了柔性附件与柔性绳网之间相互作用对控制带来的影响,可能导致理论控制效果与实际情况相差甚远。所以,目前基于TNSS模型的大多数研究主要还是聚焦于捕获阶段飞网的发射部署和拖曳阶段系统的动力学分析,少有拖曳阶段的稳定控制研究。卢山等基于TNSS模型设计了恒张力控制律,实现了对目标章动和系绳摆动的有效抑制,但所设计控制律需要配合张力切换机构,并且没能对目标柔性附件的振动进行控制。因此,我们希望在保留绳网清除技术成本优势的前提下,设计一种更加简便、高效的控制方法。
通过调研发现,面对一个像TNSS这样欠驱动、刚柔耦合且仅有单一执行器的系统,O’Connor所提出的基于波动的控制方法(Wave-based control, WBC)效果显著,并已成功实现了对TSS拖曳过程的变轨稳定控制、碎片消旋控制和碎片残余液体晃动抑制。这些研究不仅体现出波动控制具有控制形式简单、计算量小、控制鲁棒性强等优点,最为重要的是,它们的成功说明波动控制具有不依赖系统动力学模型精细程度的特性。而动力学模型的精细程度正是TNSS模型与传统TSS模型在控制方法研究中最主要的区别。因此,我们希望运用波动控制的思路,针对带有柔性太阳帆板失效卫星的绳网拖曳过程,设计一种波动控制方法来实现失效卫星姿态稳定及其帆板振动抑制。
现有的文献中还没有考虑过失效卫星绳系拖曳中的帆板振动抑制问题,本文则首次开展了基于波动控制方法的目标姿态稳定控制和帆板振动抑制研究。这是本文的核心创新点。
文章第1节提出了一种主绳上分布质量珠点的“单主绳-多分叉子绳”简化TNSS动力学模型。第2节介绍了波动控制的思想并详细说明了控制律设计过程。第3节通过数值仿真验证了控制律的有效性。最后在第4节给出结论。
1 基于Kane方法的动力学模型
以带有柔性帆板的失效卫星为目标碎片,TNSS动力学模型由拖船、绳网和失效卫星三部分组成。为提高解算效率,将拖船和失效卫星的平台简化为立方刚体,卫星平台两侧连接厚度不计的柔性帆板。同时,采用“单主绳-多分叉子绳”的绳系结构来简化绳网,其中的“单主绳”对应拖船系绳,“多分叉子绳”对应绳网中实际承力的部分,如图2所示。为了尽可能真实地体现出碎片被绳网包裹的效果,仿真时子绳连接点的数量和位置可以任意设置。

图2 绳系拖曳系统及其坐标系示意图Fig.2 Schematic diagram of tether towing system and its coordinate system
使用Kane方法对简化后的TNSS进行动力学建模,最终可以将系统动力学模型统一为一组Kane方程,即
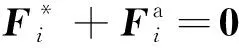
(1)
文献[32]中仅对绳网拖曳系统的动力学特性进行了分析,并未考虑控制问题。在下一节中将重点阐述控制方案的设计过程。
2 波动控制方案设计
2.1 波动控制思想简介
位置或速度的改变,是对运动最直观的认识。但如果跳出这一思维定势,从波的角度去分析运动,便能得到一种新的控制思想,即“波动控制”的思想。所谓“波动”,是将可观察的“运动”视为两列“机械波”的叠加效果。这里所说的运动指代广泛,包括位移、速度或加速度等若干与运动相关的物理量。
为了便于理解,Cleary等曾借用一个具有执行器的柔性系统来进行说明,如图3所示。当执行器主动向右移动时,弹簧弹力随长度的变化而改变,就像是一列“力波”沿着弹簧从执行器向柔性系统前进。将这种力波称为入射波,与位置和时间有关,记为(,)。入射波到达下一个质量块时,如果该质量块还连有其他弹簧,那么这些弹簧也将被拉伸而产生弹力,由此产生新的入射波继续向前传递。但如果质量块位于系统边缘,质量块不受约束的位移将逐渐使弹簧缩短,于是类似的弹力变化也可以视为一种力波往回传递。将从柔性系统边缘向执行器回传的、与入射波效果相反的力波称为返回波,记作(,)。入射波与返回波共同构成了所观测到的弹簧弹力,这便是把运动理解为两列波的叠加的原因。同样,执行器的实际位移也包含了执行器的主动位移和返回波所引起的位移。返回波对执行器位置的扰动又将引发新的入射波,最终不同的入射波和返回波将在系统中来回传递,造成了所观测到的系统振动。
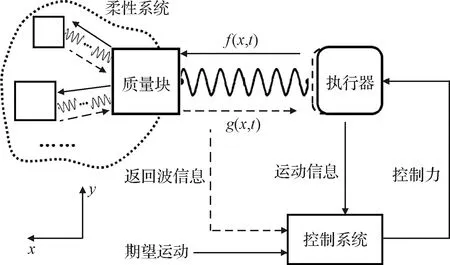
图3 波动控制原理示意图Fig.3 Schematic diagram of WBC
这样的分析方法同样适用于TNSS模型,因为如果将图3的运动拓展到三维,便几乎可以得到TNSS简化动力学模型,如图4所示。其中拖船对应执行器,系绳对应与执行器相连的弹簧,剩余部分对应柔性系统。二者的主要区别在于系绳会产生松弛现象,如果能设计控制方案保持系绳张紧,那么同样能够用上述波动思想对TNSS进行分析。
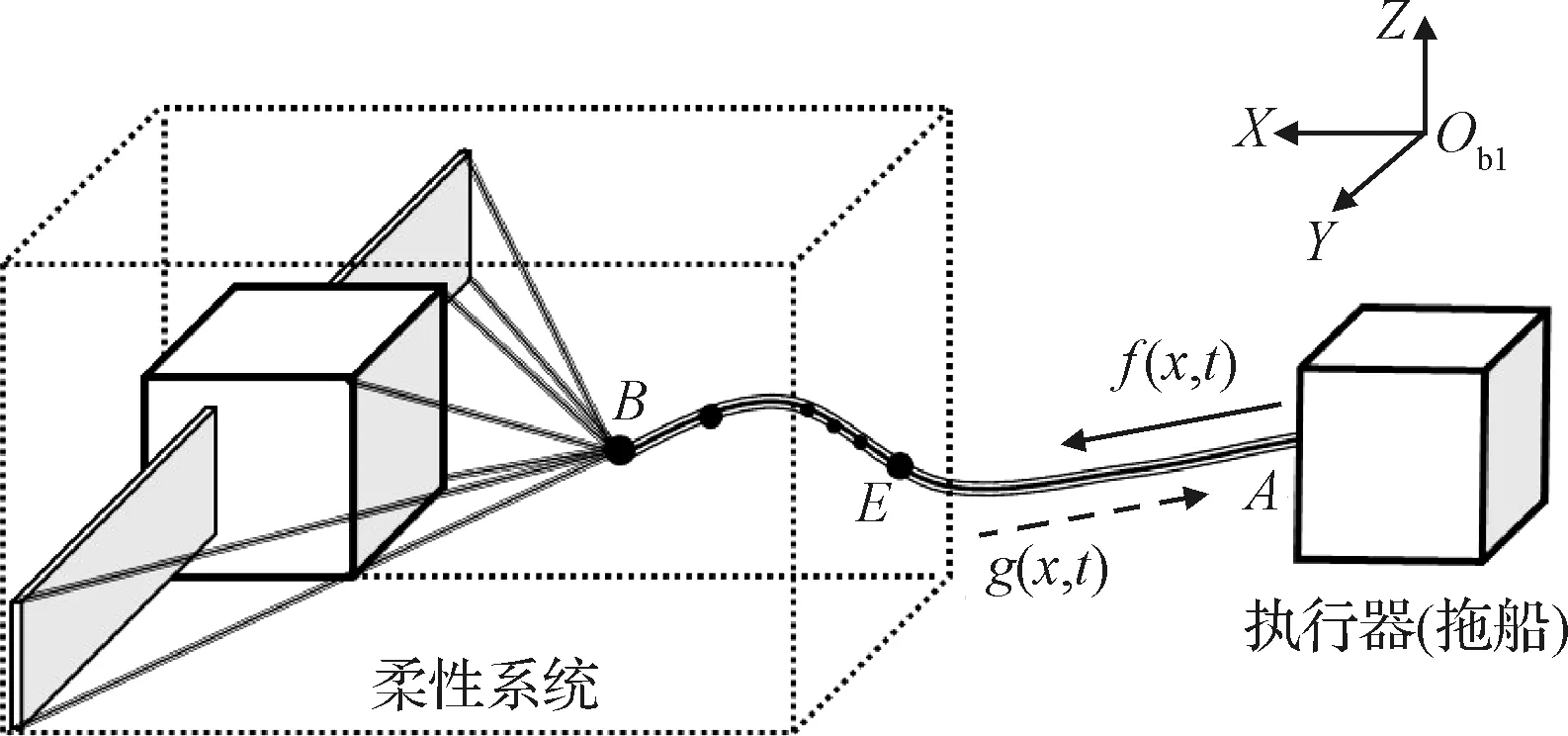
图4 TNSS的波动控制及其临时坐标系方向示意图Fig.4 Schematic diagram of TNSS wave-based control and its temporary coordinate system direction
从直观运动过程来看,希望拖船在拖曳过程中能够不断调整自身与失效卫星之间的相对位置,从而改变其受力情况,以此削弱其旋转角速度实现拖曳稳定控制与振动抑制。但实现这一控制目标并不容易。控制的主要难点在于拖船与柔性系统之间仅由一根尺度较长的系绳连接,拖船难以获得准确的输入信号,再加上柔性系统内运动耦合情况复杂,一般的控制方法反而容易加剧系统的振动。而在波动控制的思想下,可以将这一复杂的振动抑制过程转换为对系统中波的控制过程,执行器容易通过系绳来接收返回波的信息,因此波动控制成为可能。
在这样的想法下,希望所设计的控制系统能够接收并处理返回波信息,再结合期望运动与执行器实际运动,形成作用于执行器的控制力。接下来将详细推导控制律的设计过程及其参数配置。
需要说明的是,本文不考虑系绳的扭转力矩,即不考虑对碎片滚转运动的控制。因为在拖船的系绳连接处安装万向轮装置即可避免绳系结构的扭曲缠绕。
2.2 横向控制律设计
为了遵循波动方程的符号习惯,图4中建立了一个用于推导波动控制律的临时坐标系(),原点位于拖船质心,方向与拖船前进方向相反,方向沿地心指向方向,方向满足右手定则。将拖船在方向和方向的运动统称为横向运动,在方向的运动称为纵向运动,那么相应的控制就称为横向控制和纵向控制。
横向控制通过调整拖船的横向运动来改变各分叉子绳的张力,从而形成控制力矩以稳定碎片姿态。横向控制律的推导过程遵循以下假设:(1)推导过程中忽略系绳张力中的阻尼力;(2)从执行器发出入射波到接受返回波的这段时间内,系绳张力大小恒定;(3)拖曳控制过程中,拖船自身姿态保持稳定,系绳的摆动幅度较小。
以方向为例,假设初始时刻失效卫星具有偏航方向的旋转,那么拖曳过程中系绳将产生方向的摆动。选取绳上靠近拖船连接点的某一位置(,)进行分析,系绳张力大小为。根据波动控制的思想,张力在方向的分量可视为两列力波的叠加,即
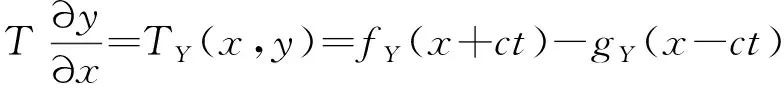
(2)
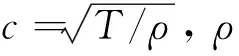
同时,系绳的横向摆动满足横波的一维波动方程,有
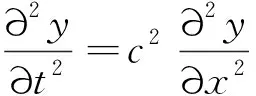
(3)
于是联立式(2)和式(3)得到绳上该位置的方向速度为

(4)

式(4)表明波与运动速度存在关联,因此联立式(2)和式(4),可以建立返回波关于速度和张力的表达式为
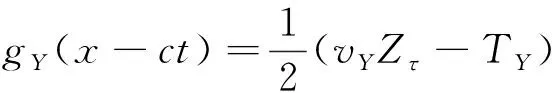
(5)
正如上一小节所说,在波动控制思想下,控制目标已经转换为了对波的控制,而式(5)将抽象的力波用可观测的物理量表达了出来,这对控制律的设计而言意义非凡。在式(5)的基础上,如果能够找到期望的波的稳态值,就能从理论上实现控制。
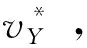
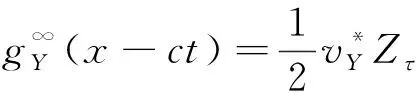
(6)



(7)

从物理意义的角度看,所设计的控制力像是一种阻尼力。设想在拖船附近方向上存在一个具有特定速度的虚拟质量体,如图5所示。质量体与拖船通过阻尼器相连,两者速度差所产生的阻尼力与所设计的控制力相同。这便是对这一时刻控制力的物理解释。

图5 所设计控制力的物理含义示意图Fig.5 Schematic diagram of physical meaning of designed control force
容易发现,由于虚拟质量体的速度表达式中包含了系绳张力分量,因此在拖曳过程中,质量体的速度是不断变化的。虚拟质量体的存在就像是一个提示器,例如,当拖船需要往方向正向移动来拉动碎片以抵消其自旋时,质量块能够通过速度变化来“提示”控制系统应当产生一个指向轴正方向的控制力。因此,只要失效卫星存在转动或振动,被拉动的绳网就会将返回波传回拖船,进而控制系统产生相应控制力,以此稳定失效卫星的姿态。
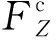
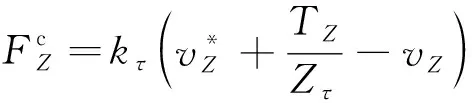
(8)
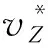
2.3 纵向控制律设计
拖船在方向移动产生的控制称为纵向控制。纵向控制主要解决两个问题,一是避免系绳松弛,保证控制系统能及时接收到返回波信息,避免拖船与失效卫星的碰撞。另一方面,要抑制帆板因拖曳而产生的振动,避免二次碎片污染。同样选择系绳上靠近拖船的位置,假设在某一较短时间内移动的距离为,由于系绳摆动角度很小,所以系绳张力的纵向分量就是张力的大小。于是,纵向张力同样可以表示为波的叠加,即

(9)
式中:是系绳的杨氏模量,是系绳截面积。
与横向控制不同的是,稳定后系绳保持拉紧的状态,张力维持在非零稳定值,即
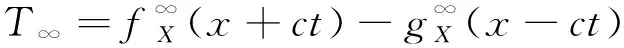
(10)
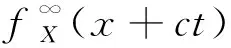
类似地,纵向运动对应的波动方程变为一维纵波方程,即

(11)


(12)
式中:是纵向波阻抗,满足关系式=。
容易发现,纵向速度与横向速度具有一致的表达形式,于是可以类比横向控制力的推导,联立式(9)和式(12),得到一般时刻返回波表达式为
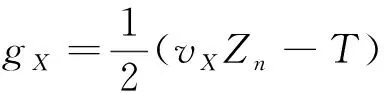
(13)
同理可得稳定后的返回波表达式为
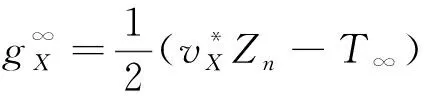
(14)
进而得到纵向控制力为

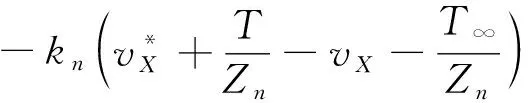
(15)
与横向控制类似,只要失效卫星的帆板产生了振动,或是系绳逐渐趋于松弛,总有偏离稳态值的返回波沿系绳传到拖船连接点。控制系统将根据式(15)产生相应控制力来调整拖船与失效卫星的相对位置。最终在控制力的不断作用下,连接点处接收到的返回波会被控制到稳定值。而在返回波趋于稳定的过程中,控制系统实现了对柔性帆板的振动抑制。
至此,详细说明了控制律的设计过程,并由式(7)、式(8)和式(15)给出了拖船三通道的控制力表达式。需要说明的是,控制系数可根据实际系统的情况选取,波阻抗的定义也只是一种参考值,可以稍微调整。根据不同的捕获目标以及拖曳情况,选择合适参数组合能够使得系统更快达到稳定状态。
3 仿真校验
基于所提出的TNSS简化动力学模型,通过数值仿真来验证控制理论的实际效果。在仿真中,质量为2500 kg的拖船在椭圆轨道上运行,轨道半长轴42164 km,偏心率0.008,轨道倾角7°,升交点赤经50°,近地点幅角230°,真近点角170°。质量为1800 kg的失效航天器与拖船相距80 m,中心刚体棱长4 m,单块帆板长6.7 m,宽2.4 m。每块帆板的顶角处连接2根子绳,中心刚体上连接4根子绳,具体位置如图2所示。其他系统仿真参数:推力、拖船与中心刚体的转动惯量矩阵和、帆板振动前三阶模态频率、帆板振动模态阻尼比和系绳阻尼系数详见表1。不考虑滚转方向的自旋,设定初始时刻失效卫星在偏航和俯仰方向均有10 (°)/s的旋转速度。施加波动控制时,单通道控制力大小限定在50 N以内。
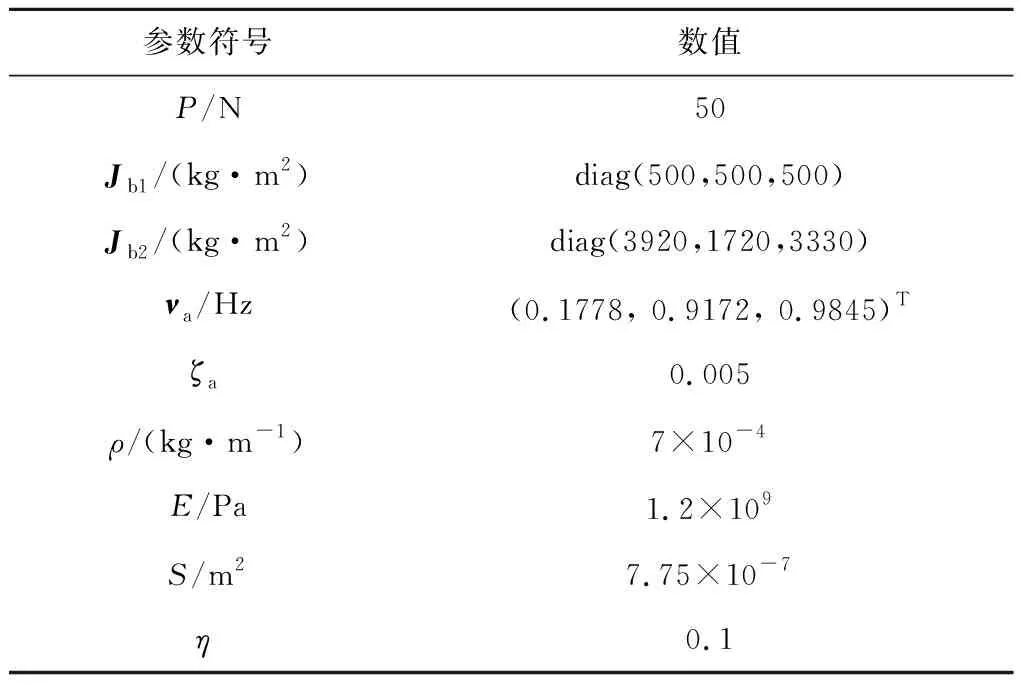
表1 系统仿真参数Table 1 System simulation parameters
图6给出了失效卫星的角速度变化情况。从无控拖曳时失效卫星的角速度变化可以看出,所建立的多子绳简化结构体现出了真实绳网的旋转阻尼特性。在绳网的包裹下,即使不施加额外的主动控制,两个方向的角速度也将随着拖曳的进行而逐渐减缓。但是,这种旋转阻尼特性是极其有限且缓慢的。以该仿真为例,当拖曳进行至2000 s时,失效卫星的角速度峰值也仅仅略小于其初始时刻的角速度。而在实际清除任务中,目标碎片长时间姿态不稳定容易引发绳网缠绕、系绳松弛、柔性附件断裂等状况,危及拖曳系统安全。因此需要通过主动控制来加速目标姿态稳定过程,确保清除任务的顺利开展。
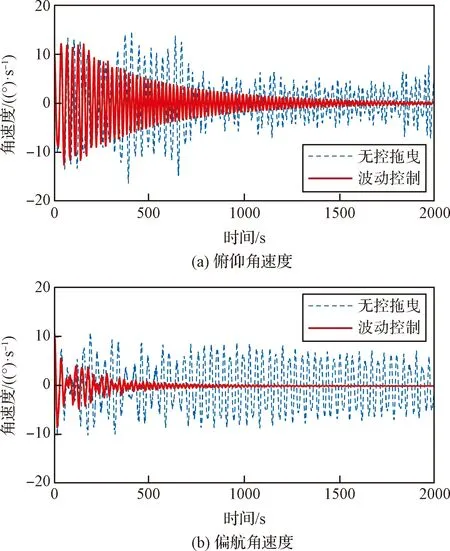
图6 失效卫星角速度变化情况Fig.6 Evolution of angular velocity of defunct satellite
在波动控制力的作用下,拖船不断调整位置以改变子绳张力分配,形成对失效卫星的控制力矩来削弱其角速度,所以两个方向的自旋角速度能够快速收敛并趋近于零。从图6中还能发现,偏航方向的角速度能被更快地控制住,这是由于柔性帆板形状细长,拖船在其长边方向的移动能够对失效卫星产生更大的控制力矩,因此控制效果更好。这一结论也从侧面验证了所设计的波动控制方法稳定碎片姿态的原理,表明了控制的可行性。
不仅是姿态扰动,帆板振动也会产生偏离稳态值的返回波。换句话说,返回波中包含姿态扰动信息和振动扰动信息。而所设计的控制力是根据接收到的返回波而变化的,因此理论上波动控制能够在稳定失效卫星姿态的同时实现对帆板振动的抑制。我们沿左侧帆板的长边方向,选取了3个不同位置处的帆板微元,给出它们在本体系下前进方向的位移,以此来刻画帆板振动情况,如图7所示。

图7 左侧帆板振动情况Fig.7 Evolution of vibration of the left solar panel
显然,如果不进行主动控制,柔性帆板将在拖曳过程中持续振动,图7(a)的仿真结果验证了这一点。弹性位移量最大的微元位于帆板上远离中心刚体的一端,位移峰值大约在0.5~1.0 m,振动周期从1.6~16 s不等,振动情况非常复杂。对于一块长度6.7 m的柔性帆板而言,这样的形变虽不至于将其直接折断,但如果长时间保持这样幅度和频率的振动,很容易使帆板材料疲劳而产生断裂。从这个角度看,施加主动控制来抑制拖曳过程中柔性帆板的振动是必不可少的。图7(b)给出了加入波动控制后各微元的弹性位移情况:各点仅在开始的短时间内有一定位移,而到大约600 s时各点的位置便已趋于稳定。这意味着在波动控制的作用下,帆板能够快速稳定至某一形变位置,随后在拖曳过程中便不再振动,说明控制是非常有效的。
对比之前复杂的振动情况,这样的变化成效显著,不仅在于振动抑制效果良好,更是因为这一切都是和姿态稳定控制同时完成的。实际上,这是横向、纵向波动控制律共同作用的结果。由于子绳附着在柔性帆板上,姿态的不稳定必然会引起帆板的振动,于是本文提出横向控制律稳定碎片姿态,为振动抑制创造了前提。进一步地,如果仅稳定碎片姿态,拖曳系统也能以类似“悠悠球”的状态相互拉扯着前进,这同样会引起帆板振动,于是设计纵向控制律以稳定拖船和碎片的相对运动,使振动抑制得以完善。巧妙的是,这两部分控制律设计都统一于基于波动的控制思想,并且控制系统仅需要观测拖船直接接收到的返回波信息来生成控制力,这便是所设计控制方法的优势所在。
最后,给出了系绳张力的变化情况,如图8所示。可以看出,加入波动控制后系绳并未产生松弛的现象,一方面避免了拖曳过程中失效卫星与拖船的碰撞,另一方面也确保了拖船能够完整地接收到系统传来的返回波信息,让控制系统正常工作。

图8 系绳张力变化情况Fig.8 Evolution of the tether tension
至此,通过数值仿真验证了所设计的波动控制方法能够同时实现对失效卫星的拖曳姿态稳定以及对其柔性帆板的振动抑制,并且控制效果非常好。
在能够取得良好控制效果的前提下,相较于其他拖曳稳定控制的研究,本文所设计的波动控制方法优势显著,体现在:(1)拖船仅通过微调与目标的相对位置,即可同时进行横向和纵向的控制,用一次控制实现两个目标;(2)不需要额外的系绳收放装置或张力控制装置,利于工程实现;(3)首次考虑失效卫星绳网拖曳中的帆板振动抑制问题。
4 结 论
本文以带有完整展开柔性帆板且具有一定自旋速度的失效卫星为目标,针对失效卫星的绳网系统拖曳清除场景,基于波动控制的思想提出了一种控制方法,并详细阐述了控制方法的推导设计过程。面对复杂的、刚柔耦合的绳网组合卫星系统动力学模型,尽管所设计的控制方法形式简单,但数值仿真证明其控制效果良好,同时实现了拖曳过程中目标碎片的姿态稳定以及对柔性帆板的振动抑制。

