一种小天体探测器绕飞轨道主动抗扰控制方法

姚文龙，杨 珂，邵 巍，刘 毅

(1. 青岛科技大学自动化与电子工程学院，青岛 266061；2. 北京理工大学宇航学院，北京 100081)

0 引 言

对小天体进行绕飞探测是完整、准确了解小天体地貌等信息最为有效的方法。而小天体探测器绕飞段导航制导任务通常会受到来自太阳光压和非球形引力等各种复杂扰动的影响，这就要求小天体探测器在复杂未知外部扰动下具备更强的抗扰能力以进一步提高绕飞轨道跟踪控制精度和鲁棒性。

考虑到迭代学习控制算法可以有效抑制重复性干扰的特点和小天体探测器绕飞段受到非球形引力摄动等扰动的重复周期性，可以利用迭代学习控制方法对周期扰动进行抑制。近年来，文献[7]针对卫星存在执行机构故障和外部干扰力矩的问题，提出一种基于迭代学习观测器的卫星姿态控制系统的鲁棒容错控制方法；文献[8]针对小行星绕飞探测任务姿态容错控制问题，设计了一种自适应迭代学习容错控制器；文献[9]提出了一种行星环绕与悬停跟踪控制器的设计方法，但其控制器需要基于误差而消除误差，即必须等到扰动作用于对象而产生误差后才能反应，这会造成控制信号响应的延迟，进而影响控制精度。若能主动从被控对象中提取扰动信息，然后设计控制器将扰动消除，可以大大降低扰动对被控量的影响，从而提高控制精度。

主动抗扰是一种不必基于误差给出控制输出，并且具有强鲁棒性和实际工程意义的控制方法，因此，实现与主动抗扰相结合的迭代学习控制方法将对提高小天体探测器的轨道跟踪控制精度具有实际意义。目前，主动抗扰多应用于四旋翼飞行器和航天器的姿态控制。文献[14]设计出了一种双闭环自抗扰姿态控制系统，文献[15]针对串级PID的四旋翼飞行器飞行姿态控制提出了一种基于自抗扰控制器的控制系统设计方法，文献[16]基于自抗扰控制技术设计了航天器姿态控制器。自抗扰控制器在处理系统内扰和外部扰动问题上具有较强的鲁棒性，其利用观测器和动态补偿的组合来实现扰动抑制并减小稳态误差，在一定程度上加快了系统反应速度，并避免了积分饱和等问题。

因此，为了提高小天体探测器绕飞轨道跟踪控制精度和鲁棒性，本文设计一种小天体探测器绕飞轨道主动抗扰轨道跟踪控制方法。首先设计迭代学习控制器抑制小天体探测器在绕飞过程中受到的周期扰动造成的误差，然后设计扰动观测器对探测器受到的系统总扰动进行估计，避免依靠附加的传感器来估计小天体探测器受到的未知不确定扰动，同时利用自适应律实时估计扰动上界，进而设计控制律对系统受到的总扰动进行主动补偿，提高误差抑制的主动性，充分考虑扰动对小天体探测器带来的影响，提高探测器绕飞段轨道跟踪控制的准确性和鲁棒性。

1 动力学模型

在小天体中心固连坐标系下，小天体探测器动力学模型描述为

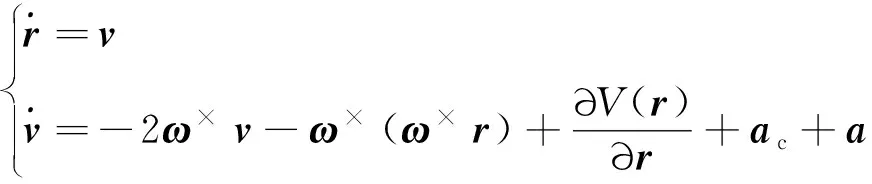
(1)

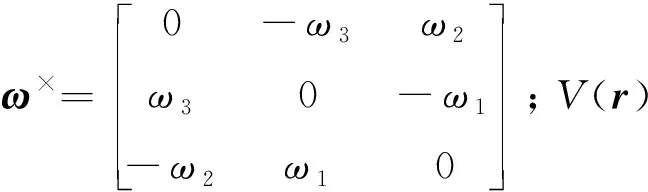
由于采用球谐函数表达的引力势能和引力场有明确的解析表达式和较高的精度，因此采用小行星的球谐函数引力势能模型：

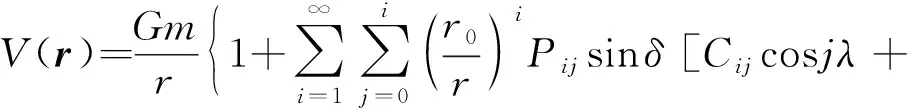
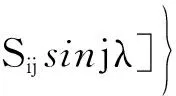
(2)

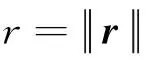
基于球谐函数引力势能模型，以243Ida小天体为例，由于引力系数高阶项的影响非常小，通常只需选取作用较大的引力系数项，则对球谐引力势能模型的前三项进行展开，小天体的引力势能函数可以写成如下形式：

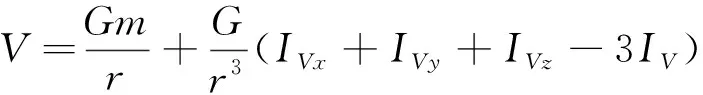
(3)

式中：=(++),,和(<<)分别为小天体绕轴、轴、轴的转动惯量。因此，可以得到

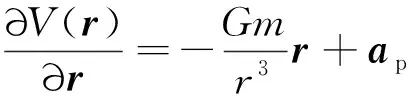
(4)

式中：=[p,p,p]=-[,,]为非球形引力摄动引起的扰动加速度，式中,,分别为

(5)

2 控制器设计

本文设计的小天体探测器绕飞段轨道跟踪控制结构框图如图1所示。

图1 轨道跟踪控制结构框图Fig.1 Track tracking control structure block diagram

2.1 迭代学习控制器设计

将位置和速度误差作为反馈控制器的输入，得到三轴上的反馈控制加速度。

对小天体探测器在受到外部未知扰动下的动力学系统式(1)，设计反馈控制器式(6)

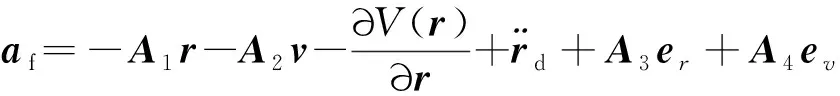
(6)

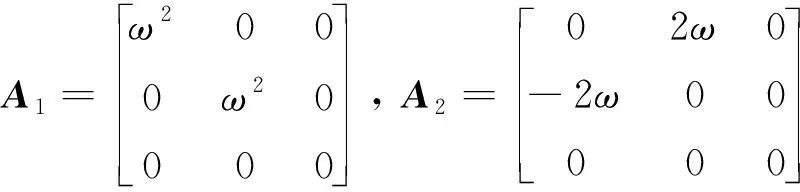
以误差向量作为状态向量，由式(1)可以得到如下动力学方程

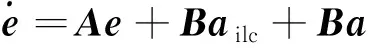
(7)

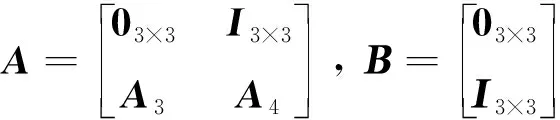
通过前一周期的迭代学习控制加速度和前一周期的误差得到当前周期的迭代学习控制加速度，即以前一周期的迭代学习控制器加速度和前一周期误差作为当前周期迭代学习控制器的输入，得到当前周期迭代学习控制器的输出。因此有如下迭代学习控制器

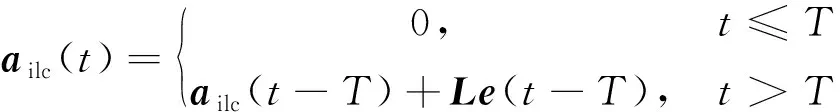
(8)

式中：=[,] · diag{,}为迭代学习控制增益，,∈为常数矩阵，,与误差相关

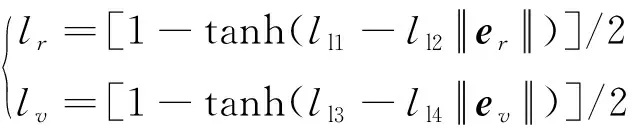
(9)

式中：系数,,,>0。

2.2 自抗扰控制器设计

根据未知扰动的实际值与扰动观测器的估计输出值之间的误差，修正扰动观测器的估计输出值，对系统受到的总扰动进行估计。结合式(1)有如下设计方程

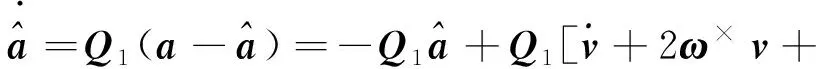
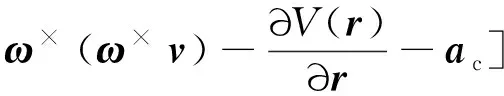
(10)

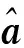
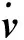
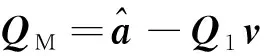
(11)

结合式(10)，对式(11)两边同时关于时间求导

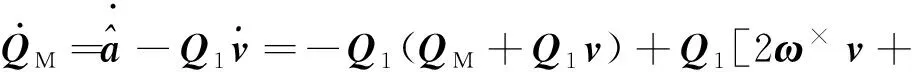
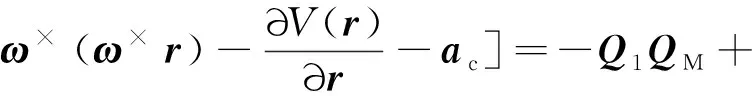
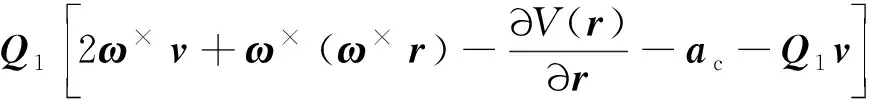
(12)

最终得到如下扰动观测器

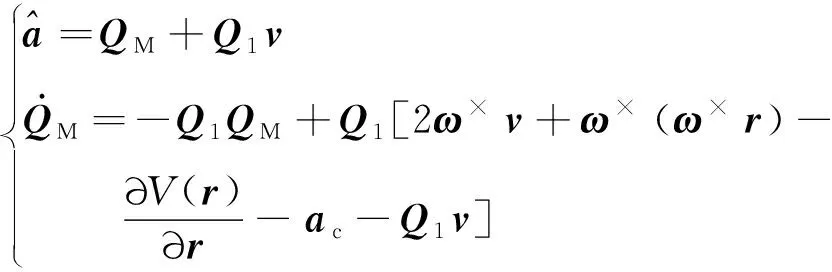
(13)

为便于分析，给出如下假设。

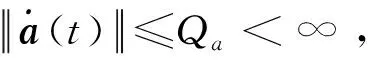
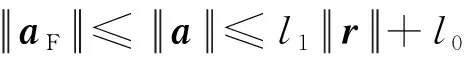
(14)

结合误差，式(14)可以转化为

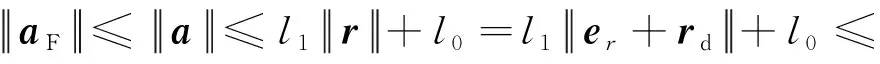
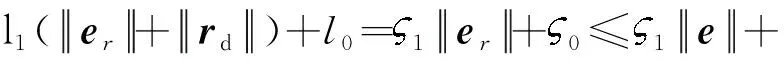
(15)

针对小天体探测器在受到外部未知扰动下的动力学系统式(1)，基于假设1，利用非线性扰动观测器(13)，可以以任意精度估计外部未知扰动，并且扰动观测误差任意小。

对所设计的扰动观测器的稳定性证明如下。

定义扰动观测误差：

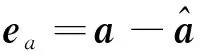
(16)

对式(13)中扰动观测器输出的扰动估计两边关于时间求导，有

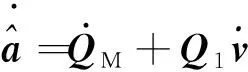
(17)

结合式(13)中间辅助状态向量和系统式(1)，得到

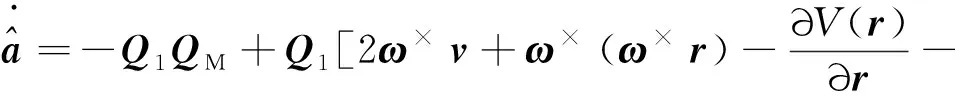
+]+[-2-()-

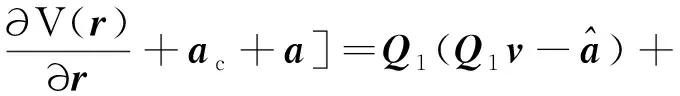
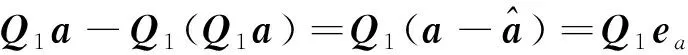
(18)

对式(16)两边同时关于时间求导，并代入式(17)，有

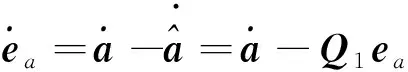
(19)

选择如下李雅普诺夫函数

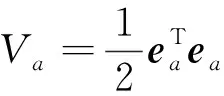
(20)

对式(20)两边同时求导，代入式(19)，有

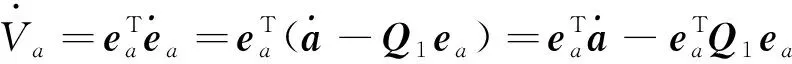
(21)

结合假设1，由杨氏不等式可知

(22)

式中：为大于0的常数。进而由式(21)得到

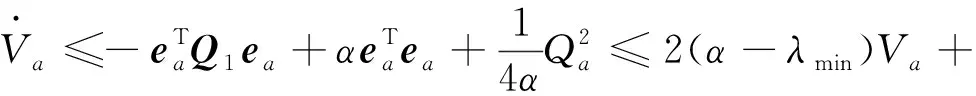
(23)

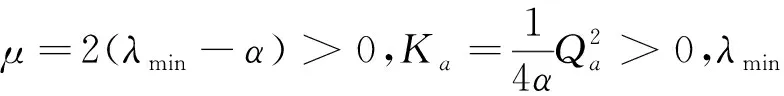
进而由式(23)得到

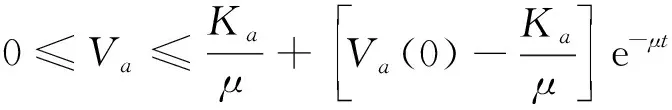
(24)

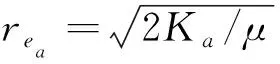
当外部未知扰动为常数向量时，扰动变化率的上界=0，根据式(23)，扰动观测器的观测误差指数收敛于0。

由于受到外部未知扰动和不规则引力场的影响，导致常推力控制发动机存在开关频繁问题，并且以非球形引力和太阳光压为主要来源的周期扰动量级多为10，为了便于绕飞任务之后继续进行后续的探测，应尽可能地减少绕飞段的燃料消耗，因此将控制死区引入到迭代学习控制律中以减少损耗。

对本文提出的反馈迭代学习控制器引入控制死区，控制方程如下

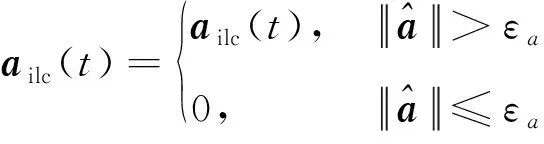
(25)

式中：>0为死区阈值。

通过所设计的扰动观测器对小天体探测器受到的扰动进行估计，将其估计输出值的绝对值与死区阈值进行比较，当大于死区阈值时，推力控制发动机才会动作，进而减少开关的频繁动作，降低燃料的消耗。

由式(1)可以得到：

(26)

式中：()=()+(),()为时刻的反馈控制加速度。

所设计的扰动观测器可对干扰进行估计补偿，故修正控制律为

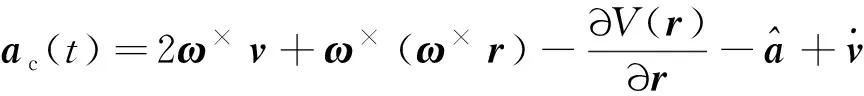
(27)

但扰动观测误差的存在会影响控制效果，因此通过自适应律对扰动观测误差的界进行估计，同时结合双曲正切函数进一步提高控制精度，所以得到优化后的控制律为

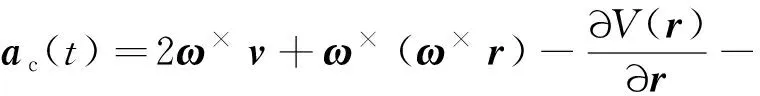
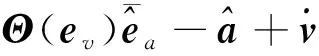
(28)

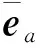
设计自适应律对扰动观测误差的上界进行估计，其表达式为：

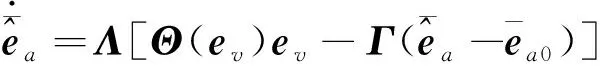
(29)

对于带死区的控制器，同文献[21]推导，由误差判断探测器受到的外部扰动来实现推力器的动作。当误差满足阈值条件而使迭代学习控制器处于死区时，推力器不动作，在推力器动作的区域内满足系统收敛，因此系统是收敛的，在有限时间内，终究会进入死区，轨道跟踪控制精度达到预期。

3 仿真分析

为了对本文所提出控制器的有效性进行校验，以小天体243Ida作为目标天体进行仿真。在小天体中心惯性坐标系下，有如下期望轨道

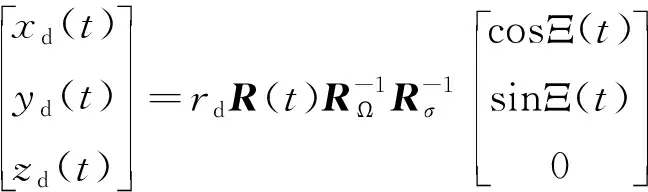
(30)

式中：为轨道半径;Ξ()为探测器在期望轨道平面上的期望方向角；旋转矩阵(),和如下

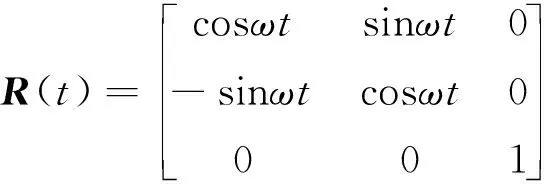
(31)

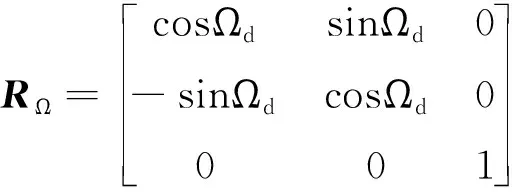
(32)

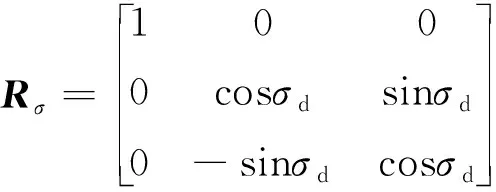
(33)

式中：期望轨道的轨道倾角=1 rad，升交点赤经Ω=05 rad。

表1 小天体243Ida参数表Table 1 Table of parameters of the small body 243Ida

采用一阶马尔科夫过程将小天体探测器受到的未知外部非周期扰动表示如下：

(34)

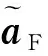
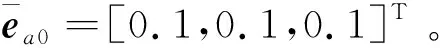
扰动观测器的相关参数设置为=diag{2,2,2},反馈控制器增益分别设置为=-3×10,=-3×10,=diag{001,001,001}。

图2为小天体中心惯性坐标系下，加入反馈和迭代学习控制后探测器的绕飞轨迹，探测器从初始位置逐渐跟踪到期望轨道，并且在之后的绕飞过程中，能够按照期望轨道运行。

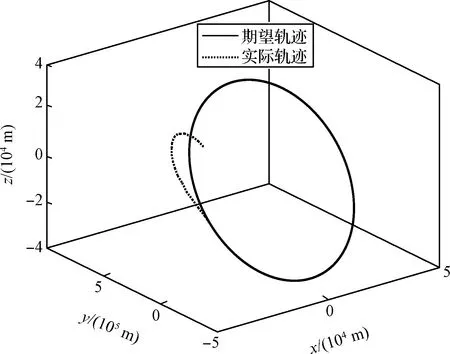
图2 探测器轨迹Fig.2 The trajectory of spacecraft

图3～6给出了最新的文献[9]中所采用的迭代学习控制方法和本文控制方法下的轨道跟踪情况。图3、图4和图5给出了小天体探测器分别在现有方法和本文控制方法下，三轴上20个周期的位置跟踪情况。

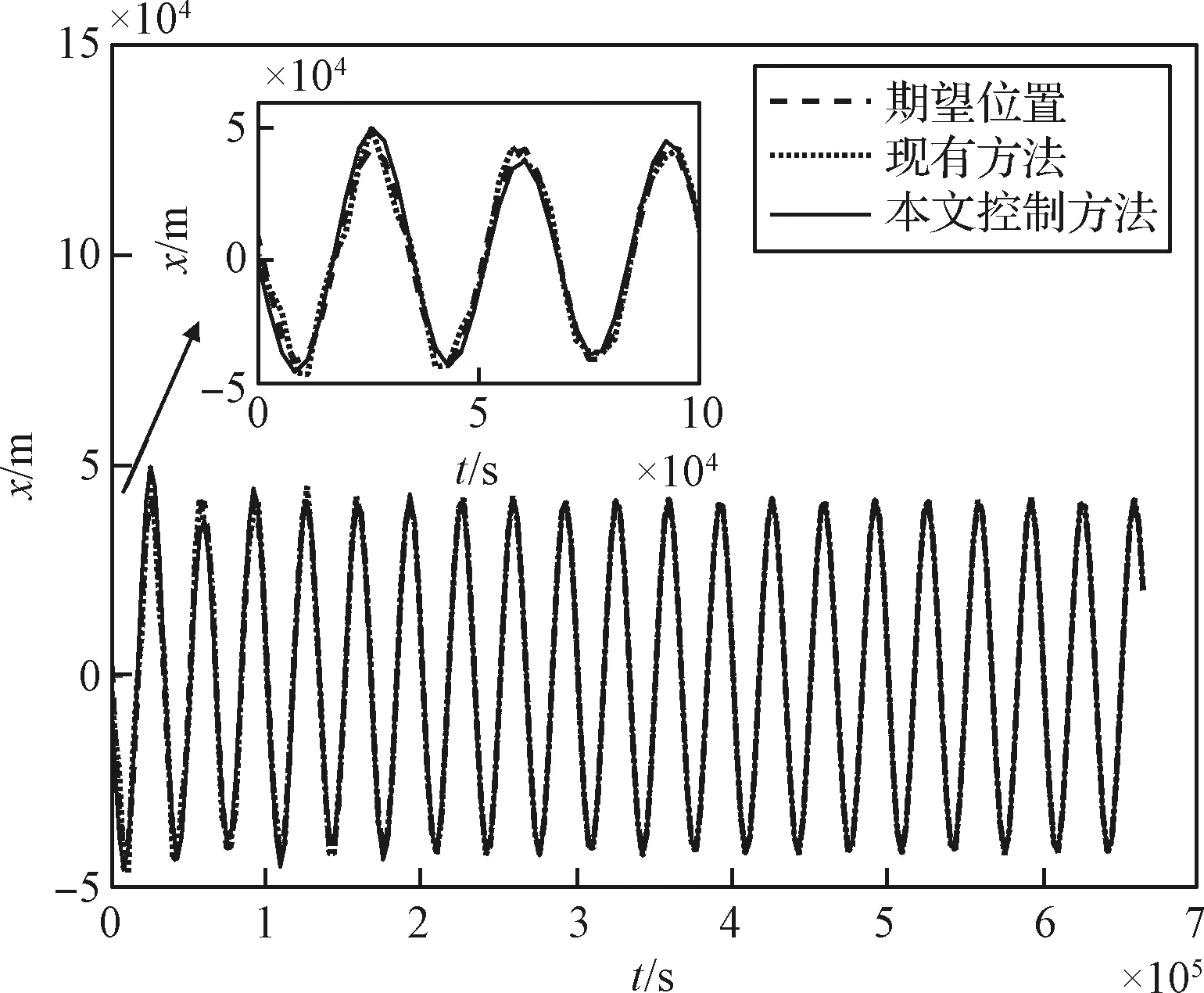
图3 探测器x轴位置Fig.3 x axis position of spacecraft

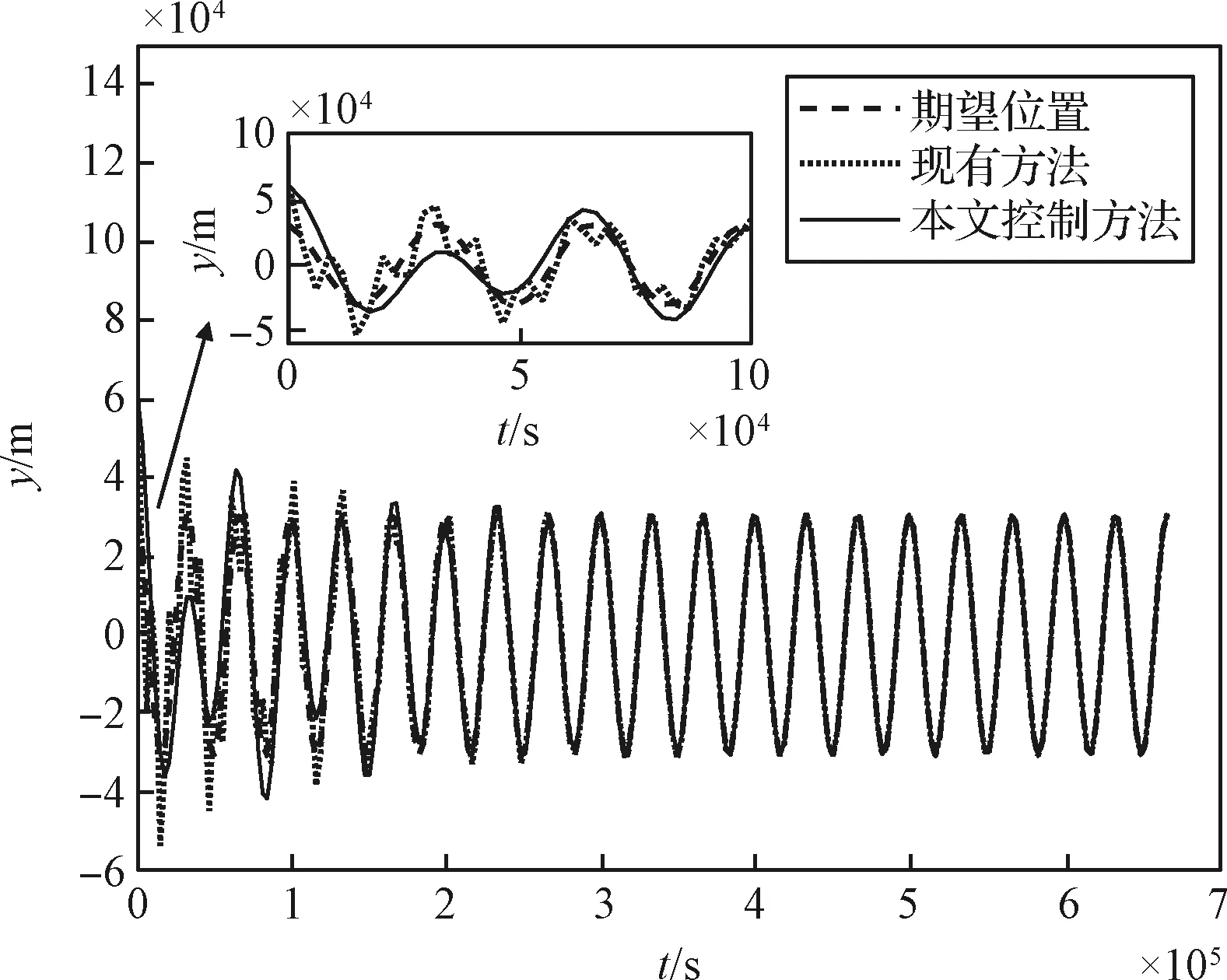
图4 探测器y轴位置Fig.4 y axis position of spacecraft

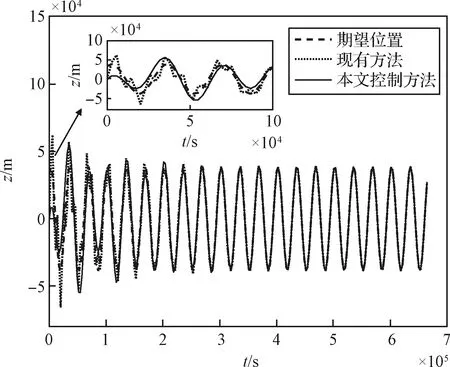
图5 探测器z轴位置Fig.5 z axis position of spacecraft

由图3～5可以看出，相同的初始条件和参数设置下，受到相同的外部扰动时，探测器的实际轨道半径在跟踪至期望轨道半径附近的过程中，相较于本文所设计的控制器，在现有反馈迭代学习控制器的作用下振荡比较剧烈。因此，可知在相同的初始条件和参数设置下，受到相同的外部扰动情况时，现有反馈迭代学习控制器与本文所设计的控制器分别作用下的闭环轨道跟踪控制系统能稳定跟踪到期望轨道，使得闭环轨道跟踪控制系统动态响应过程平稳，但后者收敛性能作用更好一些，能在更短的时间内减小位置误差，动态响应速度也更快，可以更加平缓、快速地使探测器跟踪到期望轨道，因而更适合探测器绕飞段的轨道跟踪控制。

图6给出了小天体探测器分别在现有反馈迭代学习控制方法和本文所设计的控制方法下，20个周期内的期望轨道半径和实际轨道半径。

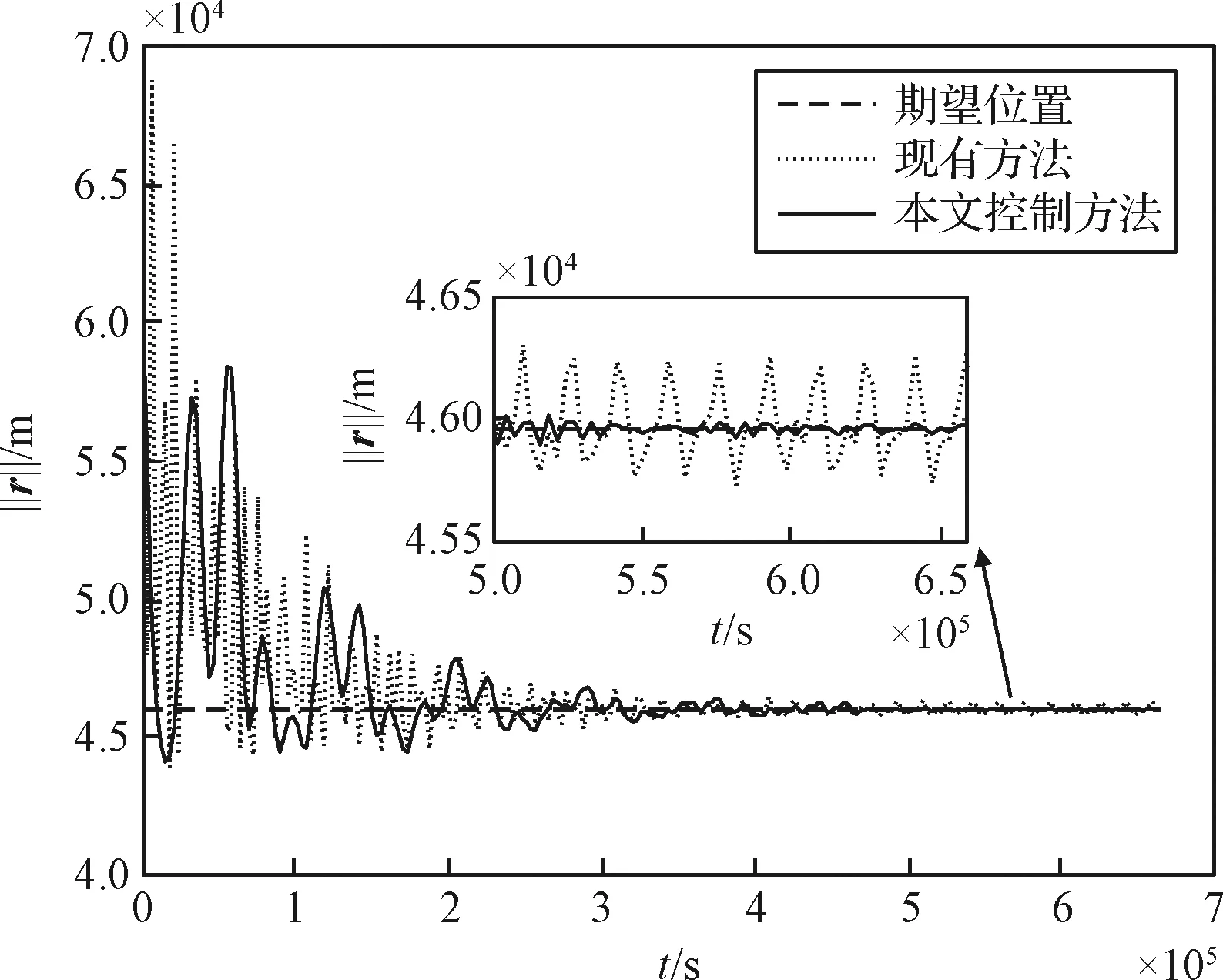
图6 探测器轨道半径Fig.6 The orbit radius of spacecraft

由图6可知，相同的初始条件和参数设置下，受到相同的外部扰动时，探测器的实际轨道半径在跟踪至期望轨道半径附近的过程中，相较于在本文所设计的控制器的作用下，在现有反馈迭代学习控制器的作用下，振荡较为剧烈，并且在20个周期之后，本文控制方法下的探测器振动幅度更小，更平稳。

由图1～6可知，小天体探测器在相同的初始条件和参数设置下，受到相同的外部扰动影响时，由本文所设计的控制器进行控制时，相较于现有反馈迭代学习控制器能够在更短的时间内减小位置误差，动态响应速度更快，振动幅度更小，需要消耗的燃料也更少，因而更适用于探测器绕飞段的轨道跟踪控制。

4 结 论

针对复杂未知扰动下，小天体探测器绕飞段轨道跟踪存在的轨道机动频繁、跟踪控制精度差等问题，提出了基于观测器及迭代学习控制的主动抗扰控制方法。该方法首先设计扰动观测器估计系统受到的总扰动，然后设计反馈控制器通过位置、速度误差信号得到反馈控制加速度抑制非周期扰动误差，进一步利用绕飞段探测任务的周期性设计带死区的迭代学习控制器抑制周期扰动误差，避免推力控制发动机频繁动作，节省成本，更进一步地，利用观测器的扰动估计值对控制律进行设计，实现对总扰动的主动补偿。相比于现有迭代学习控制方法，本文控制方法下的迭代学习控制加速度幅值的减小主要原因在于主动抗扰对总扰动的补偿，其次是由于提高控制精度后，位置的变化造成扰动加速度的不同，这使得所产生的迭代学习控制加速度也不相同。最后仿真结果表明在相同的扰动和系统参数设计下，本文控制方法可以有效提高小天体探测器的跟踪控制精度，减少燃料消耗。