星箭分离减冲击环结构优化设计

朱 璐，李 响，胡迪科，周政言

(1.北京理工大学宇航学院，北京 100081； 2. 上海宇航系统工程研究所，上海 201109)

0 引 言

星箭分离过程中产生的高频、高量级冲击载荷对于星上晶振及其它电子产品和光学产品来说是最严酷的力学环境之一。为确保卫星上这些冲击敏感器件的可靠性，一般在卫星与火箭支架之间安装减冲击结构。目前主要研究的减冲击结构有两类：(1)柔性材料(如橡胶、硅胶等)制成的缓冲垫圈，通过材料大变形吸收冲击能量；(2)采用金属材料垫片，通过间断面对冲击波的反射和折射降低冲击能量。除了上述简单的垫圈和垫片结构，减冲击环结构近年来日益受到关注。文献[9-10]中仅给出了减冲击环的结构样式，并未进行相应的结构分析和设计，文献[7-8]从冲击波传递角度分析了减冲击环的减冲原理，并做了相应的冲击实验，验证了结构减冲的有效性，但结构参数直接给定，并未开展结构优化设计，也未分析各结构参数对结构性能的影响。与一般结构设计问题相比，减冲击环结构的载荷更为极端，主要频率范围在1×10～1×10Hz，加速度幅值高达3×10～3×10g，而持续时间通常为几毫秒，结构形式也较复杂(采用分层、分块形式，同时具有离散和连续设计变量)，这在一定程度上增加了结构优化设计建模与求解的难度。

现有研究中，卫星在轨运行过程中微振动动力学环境下的振动抑制结构分析与设计受到了大量关注，微振动的持续时间长，频率一般低于200 Hz，属于稳态过程，常采用正弦扫频激励(频率按照一定规律变化的正弦激励)作为输入载荷。而本文探讨的星箭分离的强冲击环境的持续时间很短(一般为几毫秒)，且含有大量高频成分(达到上千赫兹)，准确描述该冲击载荷十分困难，早期采用的简单正弦波、后峰锯齿波和梯形波载荷形式并不能真实的地模拟冲击环境。近年来，冲击响应谱(Shock response spectrum, SRS)方法在星箭分离冲击动力学研究中得到了广泛应用，它能真实地反应出瞬时冲击载荷下不同频率结构的最大响应，陆续成为星箭分离冲击试验中的载荷规范。但冲击响应谱采用的是等效损伤的思想，描述结构频率与结构最大加速度响应之间的关系，并不直接描述载荷的时间历程，在进行结构冲击响应模拟时，需将规定的冲击响应谱转化为相应的时域载荷。文献[21]采用合成小波中的正弦窗波作为基本波形，计算出在冲击响应谱精度要求范围内的时域曲线。文献[22]利用三组脉冲函数、正弦函数和修正的Morlet小波函数推算冲击响应谱的时域曲线，使用遗传算法优化基函数的系数。文献[23]提出了一种低频域采用小波技术，中高频域采用阻尼正弦技术进行加速度时域信息合成的新方法。

本文以一减冲击环结构为对象，分析了它实现减冲击的力学原理，采用冲击响应谱的时域合成方法，计算得到符合冲击响应谱规范的时域载荷，并以此作为结构优化设计时的载荷工况。在此基础上，建立起以质量最小为目标，以减冲效果、刚度和强度为主要约束的减冲击环结构优化设计模型，该模型是一包含离散变量和连续变量的混合优化问题；分别以CATIA与ABAQUS作为结构建模和分析工具，MATLAB作为冲击谱计算工具，采用代理模型策略和自适应模拟退火算法(Adaptive simulated anne-aling, ASA)求解了该优化问题，在得到的最优结果处开展敏度分析，得到了主要性能指标对设计变量的敏度信息。本文的工作对于强冲击动力学环境下的航天器结构分析与设计有一定的指导意义。

1 减冲击环结构模型与原理

卫星-减冲击环-支架结构整体示意图如图1所示。其中，卫星结构用质量块代替，减冲击环结构安装在卫星和支架之间，星箭分离过程中火工品解锁产生的爆炸冲击载荷经过减冲击环结构后到达卫星。

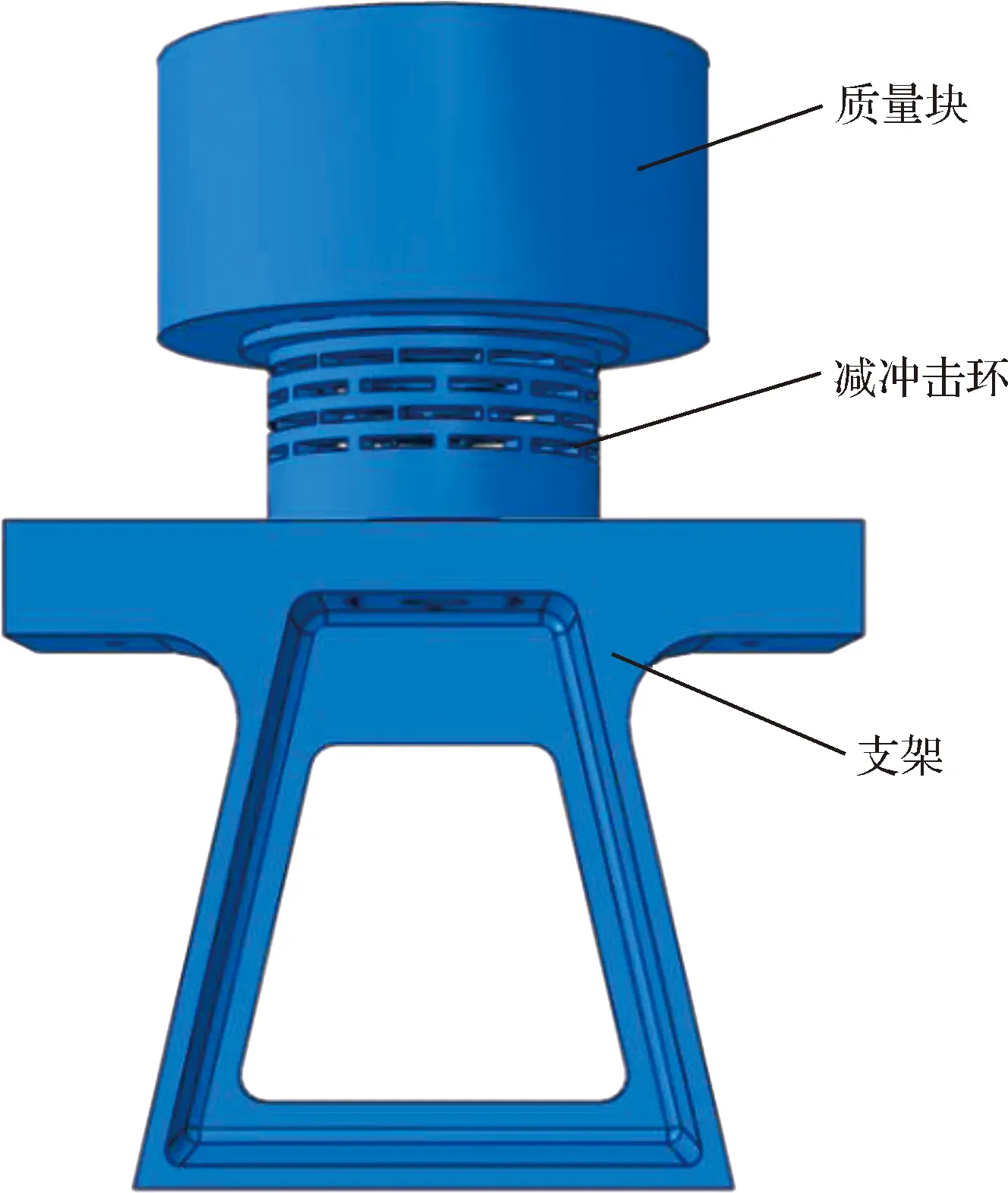
图1 星箭分离装置整体结构示意图Fig.1 Scheme of satellite-rocket separation system

减冲击环结构如图2所示，由连续层的金属环和均匀分布的支撑块交错组成，该结构可看作多个图2右侧所示元结构组成。减冲击环结构实现减冲击的原理可从能量转换与应力波传递两方面进行解释。从能量转换角度看，冲击载荷经支撑块D到达连续层C，连续层C可看作支撑块A,B之间的横梁，该梁发生弯曲变形将冲击能量转化为横梁弯曲变形后的弹性势能。而整个减冲击环结构可以看作是由多个这样的具有能量转换功能的元结构组成，从而有效实现了减冲击功能。从应力波传递角度看，减冲击环不连续的结构形式延长了冲击波到达卫星的路径，同时导致应力波的反射和折射，实现冲击载荷衰减。

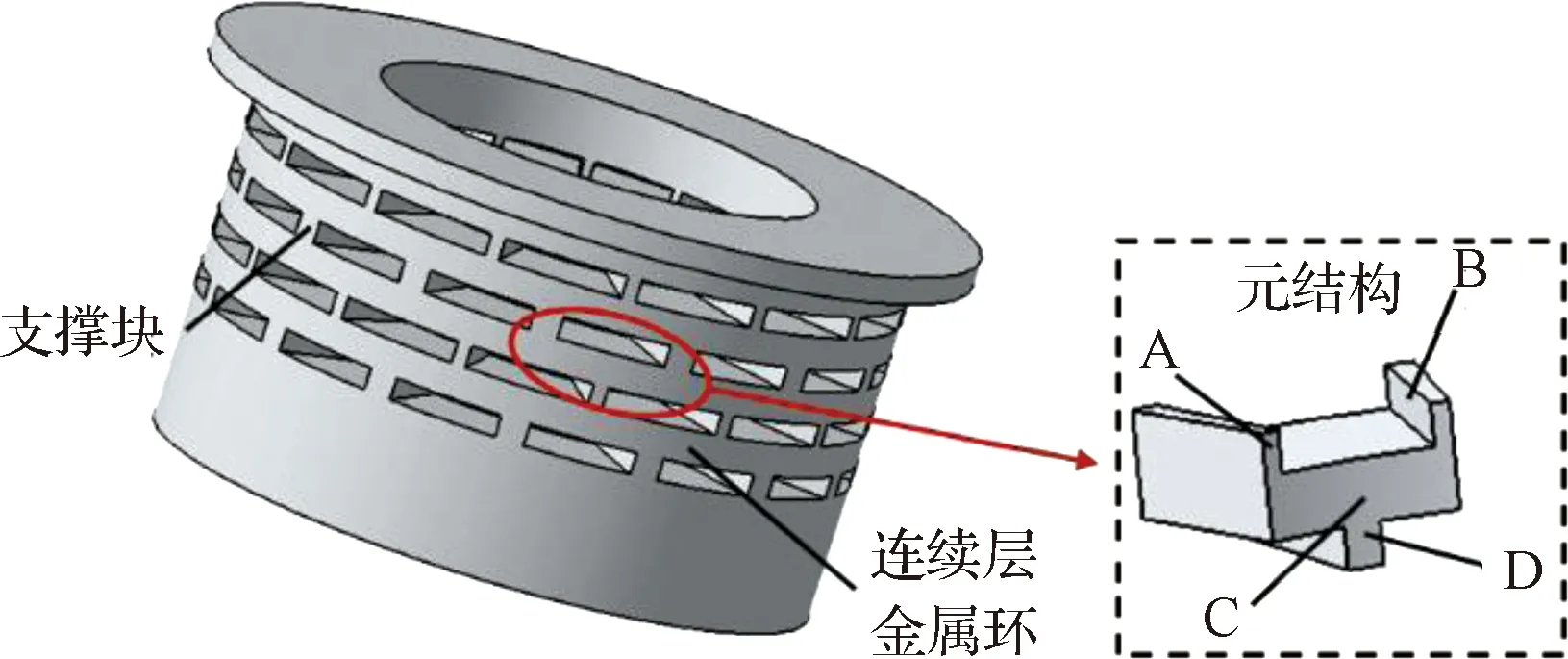
图2 减冲击环结构模型图Fig.2 Structural model of a shock isolation ring

从以上分析可见，减冲击环的层数、每一层的支撑块数(支撑块数量决定了横梁的跨度)，以及连续层的外半径和内半径、支撑块层的高度、连续层的厚度等尺寸等都会影响减冲击的效果，而上述参数同时又会影响结构的刚度和强度。因此，需要综合分析权衡该结构性能，进行优化设计，在第3节中将对此详细探讨。

2 冲击响应谱时域合成

相对于其它结构，减冲击环特有的力学环境在于其承受的短时、强烈的分离冲击载荷，因此，准确、合理地描述该冲击载荷是后续结构分析与优化设计的基础。前已说明，简单的正弦波、后峰锯齿波和梯形波等形式不能真实描述星箭分离时的冲击载荷，因此本研究利用冲击响应谱合成时域载荷。一个典型的冲击试验参考谱如图3所示，相应的主要性能数据见表1。

表1 冲击响应谱参数Table 1 Shock response spectrum parameters

图3中的冲击响应谱描述的是结构频率与结构最大加速度响应之间的关系，并未给出冲击载荷的时间历程，不能直接用于结构的冲击响应分析。它实际给出的是载荷规范，即根据时域载荷计算出的冲击谱应在图3中的上、下容差范围内。本研究中采用正弦窗波方法合成满足冲击谱条件的时域瞬态波形作为输入载荷模拟复杂的冲击环境。在该方法中包含三个主要步骤，即根据参考冲击谱计算时域载荷、校验时域载荷和修正时域载荷，分别阐述如下。

2.1 根据参考冲击谱计算时域载荷

采用合成小波中的正弦窗波，合成后的时域波形满足在初始和最终时刻加速度、速度、位移数值为零的特性，合成后的基本波形函数为：

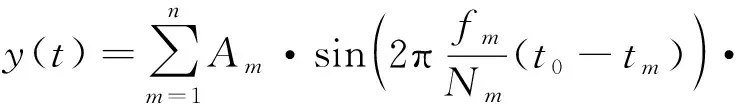
sin(2π(-))

(1)

式中：为基础波形的总数目；为第个基波的波形延迟时间；为时域波形的持续时间；,,分别为第个基波的幅值、频率、半正弦波的总数目。的采样频带取1/12倍频程变化，根据参考冲击响应谱的最低频率和最高频率可以求得基波的总数目。根据半正弦波的数目和基波频率可以求得基波持续时间，根据可以求得基波波形的延迟时间。

按上述方法，由图3中冲击谱计算得到的时域载荷如图4所示。

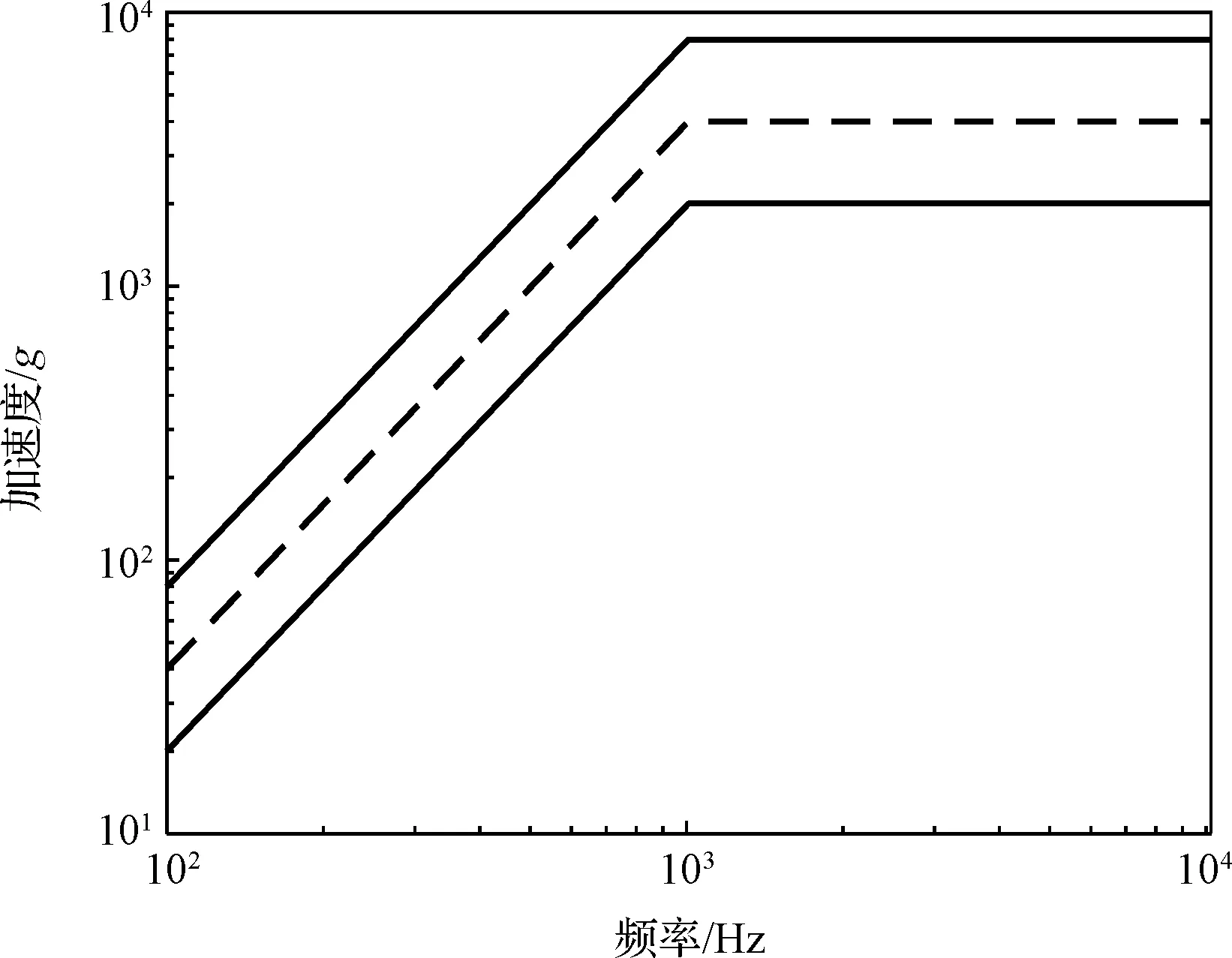
图3 典型冲击响应谱及上下容差Fig.3 Typical shock response spectrum and tolerances

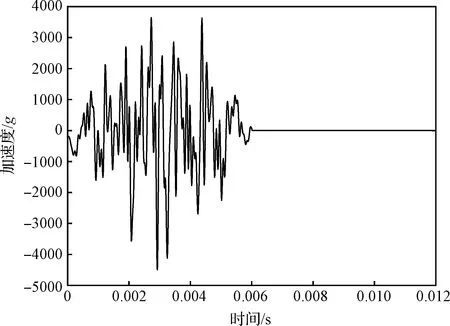
图4 时域合成的载荷曲线Fig.4 Time-domain synthesized load curves

2.2 校验时域载荷

预设的基础波形的幅值关系式为：

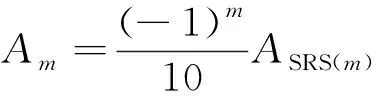
(2)

式中：为基波幅值；SRS()为对应的参考响应谱的值。由于和SRS()并不是简单的线性关系，式(1)计算得到的时域载荷并不一定满足图3所示的冲击谱规范，需进行校验，即计算图4中时域载荷的冲击谱，并与图3中的冲击谱规范对比。冲击响应谱是基于加速度时域曲线的计算函数，它将加速度时域函数作为基础激励作用于一系列的单自由度质量阻尼系统，最后建立固有频率为横坐标、系统响应峰值为纵坐标的曲线。其单自由度系统的运动方程可以表示为：

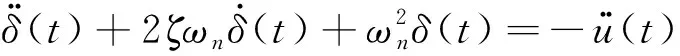
(3)

()=()-()

(4)

式中：()为质量块与基座之间的相对位移；()为质量块的绝对位移；()为基座的绝对位移；为单自由度系统的固有频率；为阻尼比。本文采用改进的数字滤波法进行冲击响应谱的计算，则冲击响应谱的递推公式为：

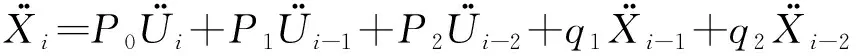
(5)

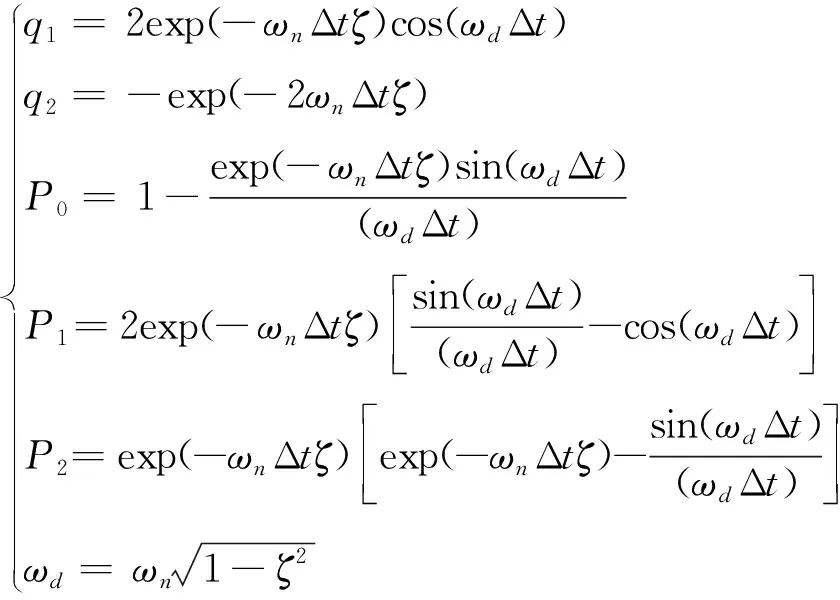
(6)

经过上述计算，可以得到图4所示合成的时域载荷对应的冲击响应谱如图5所示。从图5可以看出，由图4中合成的时域载荷求得的冲击响应谱尽管基本符合给定的冲击谱要求，但仍有部分并不在参考冲击响应谱的容差范围内，因此需要对时域波形进行修正。

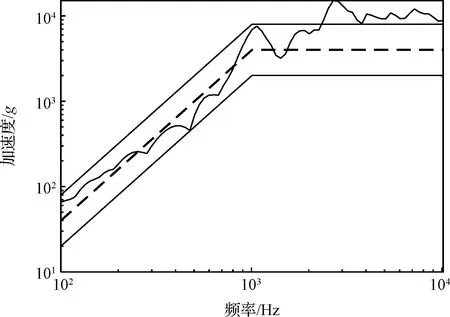
图5 时域载荷修正前的冲击响应谱Fig.5 Shock response spectrum before time-domain load modification

2.3 修正时域载荷

由于合成波形中参数对响应谱曲线的敏感度最大，因此对基波幅值进行修正，使合成的时域波形计算出的冲击谱在容差范围内，修正公式如下：

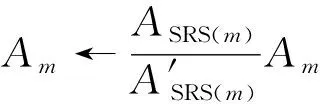
(7)

式中：SRS()为点对应的参考响应谱的值；′SRS()为点对应的时域波形合成的冲击响应谱的值。

将修正后的基础波形幅值代入式(1)计算时域载荷()，然后据式(5)计算对应的冲击谱，重复这一过程直至合成的时域波形满足容差范围。修正后最终得到的时域载荷曲线及对应的冲击响应谱曲线如图6所示。冲击响应谱时域合成的基本流程如图7所示。

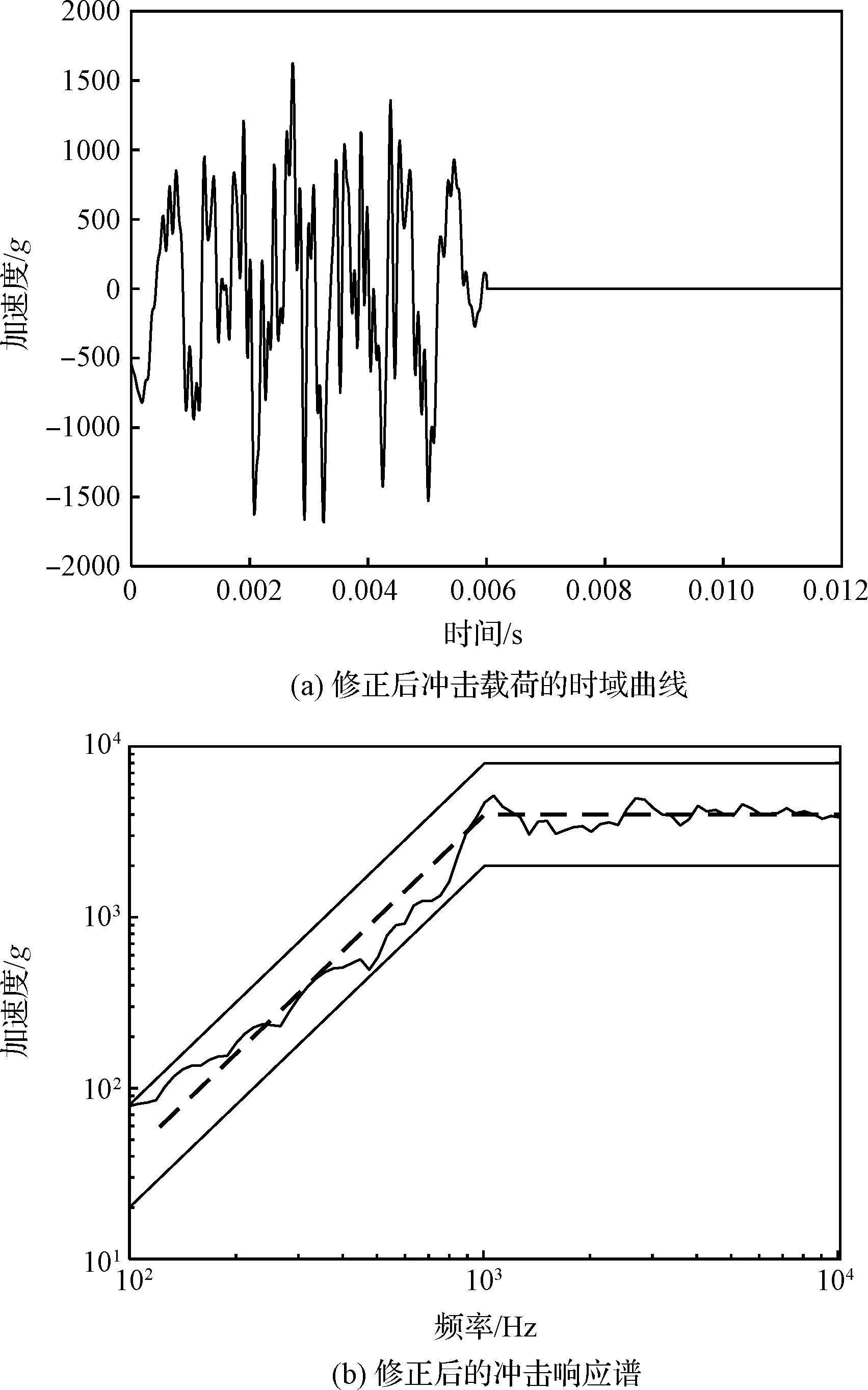
图6 修正后的时域曲线和冲击响应谱曲线Fig.6 Revised time-domain load curve and shock response spectrum curve

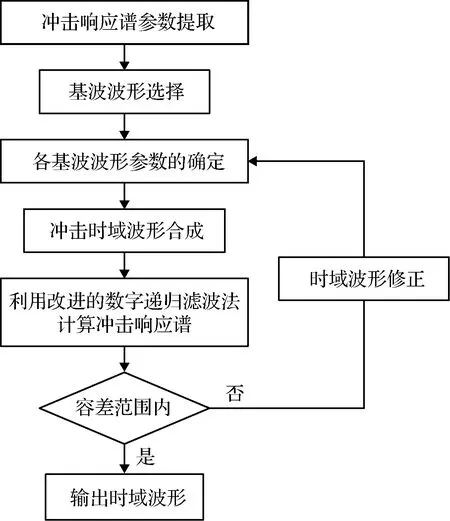
图7 冲击响应谱时域合成流程图Fig.7 Time-domain synthesis flow chart of the shock response spectrum

至此已得到满足冲击响应谱条件的时域冲击载荷，为后续减冲击环的结构分析与优化设计创造了条件。

3 结构优化设计与敏度评估

在得到合理的冲击载荷后，本节中开展以质量最小为目标，同时满足减冲效果、刚度和强度约束等关键约束条件的减冲击环结构优化设计，并在最优设计点处进行敏度评估，以获取主要性能指标对设计变量的敏度，深化对减冲击环结构性能的认识。

3.1 优化设计问题模型

结构在CATIA平台下建模，并导入ABAQUS平台进行结构分析，有限元模型如图8所示，其中减冲击环结构采用八节点六面体线性缩减积分单元(C3D8R)模拟，单元数量94911个，加载点C位于支架的下端爆炸螺栓起爆点附近。

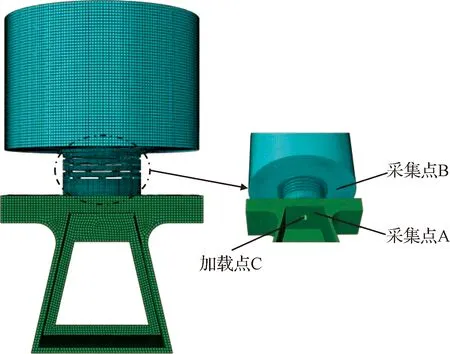
图8 星箭分离装置有限元模型图Fig.8 The finite element model of the satellite-rocket separation system

..设计变量选取

根据图2中的减冲击环结构形式，本设计中选用连续层数、单层支撑块数、连续层厚度、支撑块层的高度、减冲击环的外半径和内半径为设计变量，=[,,,,,]，如图9所示。

设计变量单位、初值与取值情况如表2所示。在上述6个设计变量中，,是离散变量，给出了全部取值，而,,,是连续变量，给出了取值上、下限。对应的优化设计问题将是一同时包含离散变量和连续变量的混合优化问题。

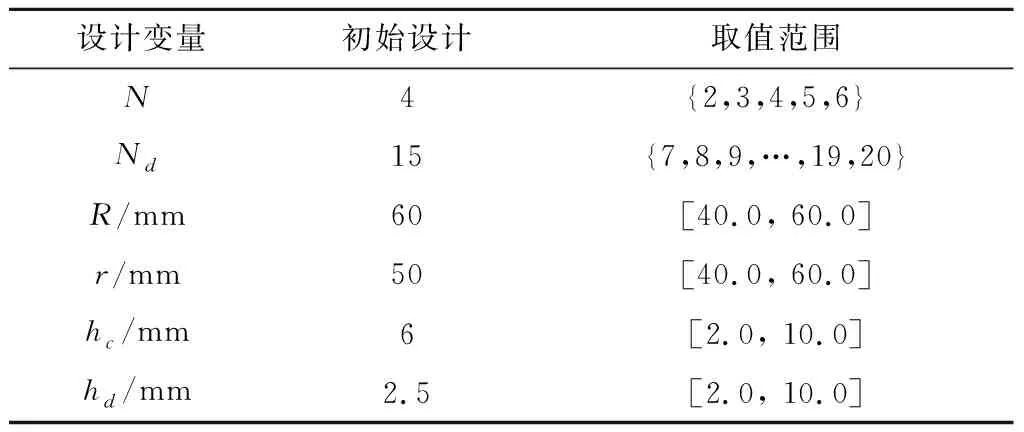
表2 设计变量的取值范围和初始值Table 2 Value ranges and initial values of design variables

..目标函数

轻质化始终是航天器结构设计的一个重要指标。本研究中以减冲击环的质量()最小为目标函数，数学描述为：

min=()

(8)

..设计约束

1)减冲效果约束

对减冲击环而言，减冲效果是最重要的约束要求。分别在如图9所示的A点位置和B点位置采集减冲前、后的加速度信息，利用改进的数字滤波法计算A、B点的冲击响应谱。减冲效果约束表达如下：

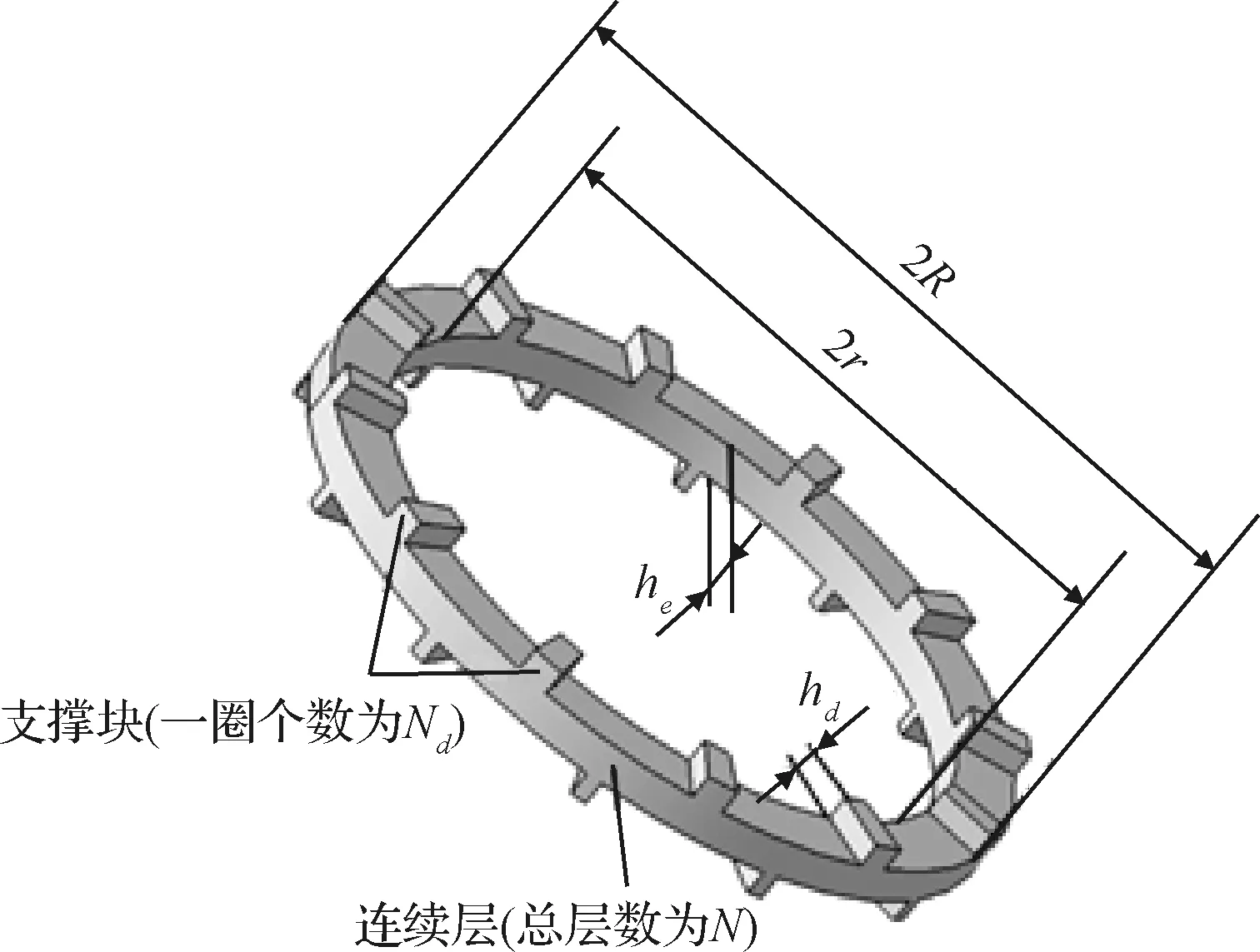
图9 设计变量示意图Fig.9 Schematic diagram of design variables

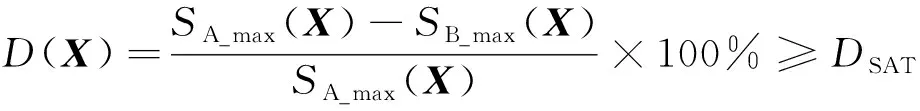
(9)

式中：()为A点的冲击响应谱的最大值(减冲前)；()为B点冲击响应谱的最大值(减冲后)；为减冲效果值；为减冲效果的允许值，本研究中取值80%。

2)刚度约束

从减冲角度看，结构刚度越小越有利于提升减冲效果，但过小的刚度又会导致减冲击环频率的减小，降低结构的整体频率，从而影响卫星的发射姿态，因此提出减冲击环结构刚度约束如下：

()≥

(10)

式中：为最小允许刚度值，本研究中取值2.8×10N/m；刚度是设计变量的函数，计算公式推导如下。

将图2中的元结构简化为两端固支的梁，如图10所示。该梁为三次超静定结构，取简支梁为基本体系，根据位移协调条件建立力法方程为：

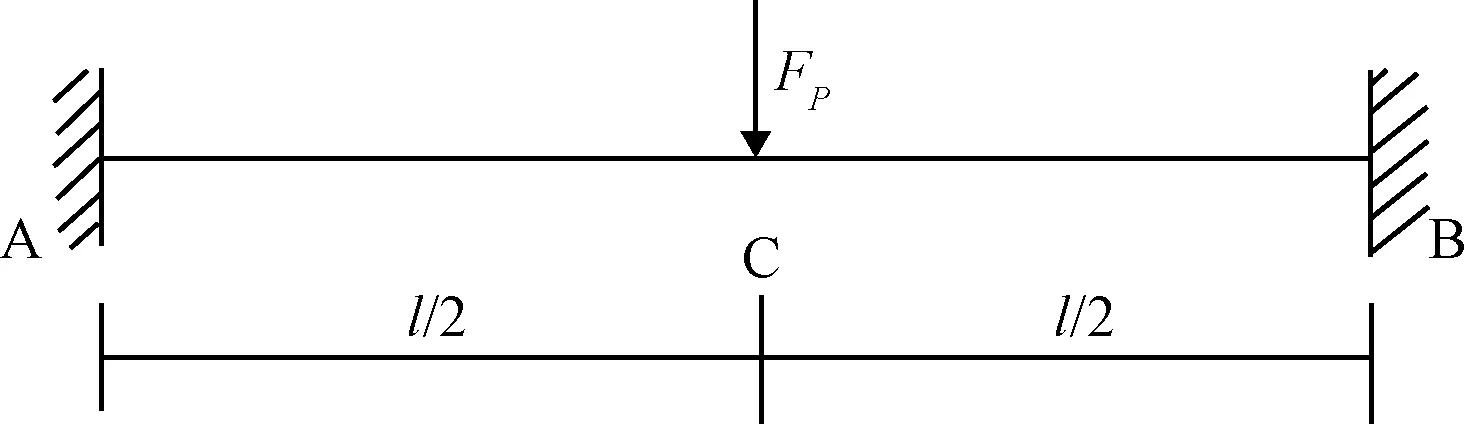
图10 固支梁示意图Fig.10 Scheme of a fixed beam

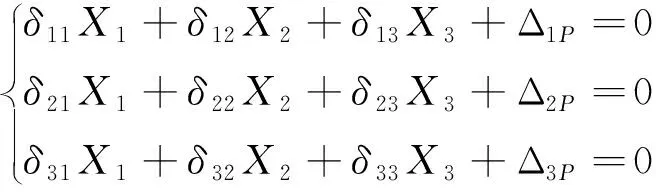
(11)

式中：为基本未知力；为仅由=1作用产生的方向的位移；为仅由=1作用产生的方向的位移；Δ为自由项。

求解上述方程并进行相关计算，利用分段积分法计算挠度方程可得C点的挠度为：

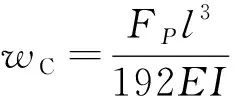
(12)

式中：为固支梁承受的集中载荷；为固支梁AB段的长度；为材料的弹性模量；为梁截面惯性矩；为C点的挠度。

固支梁长度可由减冲击环的尺寸计算得出为：

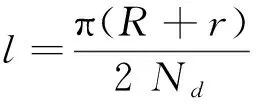
(13)

固支梁的横截面近似为矩形，故其惯性矩为：

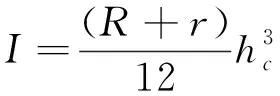
(14)

根据等效刚度计算公式，每个元结构的刚度可以表示为：

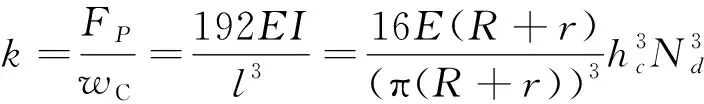
(15)

每层的元结构之间相互串联，层与层之间相互并联，根据串并联等效刚度计算的基本原理可以求得总刚度为：

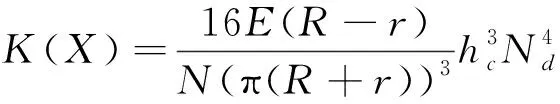
(16)

3)强度约束

强度约束一般针对火箭发射阶段提出，本研究中发射时的载荷工况为卫星等效质量575 kg，纵向过载6，横向过载2。

(17)

式中：为材料的屈服强度，本研究中材料选取Ly12铝，为413 MPa；为安全因子，取值1.5。

至此，建立起的减冲击环结构优化问题的数学模型如下：

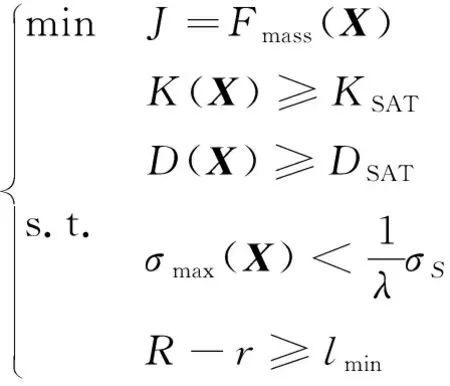
(18)

式中：=[,,,,,]为设计变量；=2.8×10N/m；=80%；=413 MPa；=2 mm。

3.2 优化设计求解

在式(18)所示的优化问题中，减冲效果约束计算需要在CATIA、ABAQUS(Explicit)和MATLAB(用于计算冲击谱)平台下完成，而强度约束计算需在CATIA、ABAQUS(Standard)平台下完成。为能在跨平台环境下使优化计算迭代过程自动运行，优化求解采用了代理模型方法，即首先在多个样本点上进行结构分析，得到相应的减冲效果数据和应力数据，并据此构建响应面近似模型，优化计算基于该近似模型进行。此外，前已说明，式(18)所示的减冲击环结构优化问题是一包含离散变量和连续变量的混合优化问题，因此经典梯度优化算法不适用，采用非梯度自适应模拟退火算法。

1)代理模型构建与检验

本文采用四阶多项式响应面模型构建近似模型，采用最优拉丁超立方实验设计方法，在设计变量的取值范围内抽取216组样本点并计算出减冲效果和最大应力，并利用上述输入输出数据拟合出响应面模型。筛选排除对拟合结果影响较小的项，最后拟合得到的响应面近似模型的表达式为：

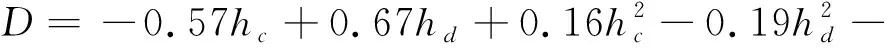
0024+00018-00056-

00035-0001+00082+

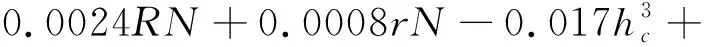
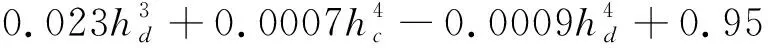
(19)

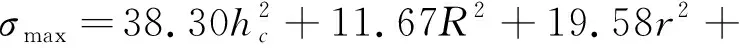
2621-2088-2116+

2530-488-2898+

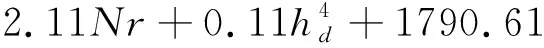
(20)

响应面模型和样本数据的拟合精度采用均方根误差相对值和决定系数来评估，其表达式如式(21)和式(22)所示。

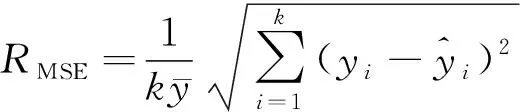
(21)

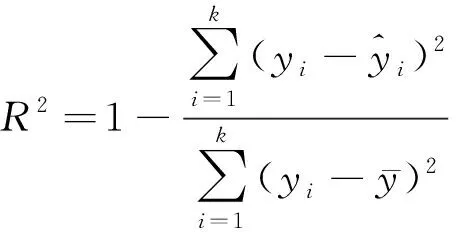
(22)

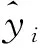
误差分析计算后，可得关于的响应面近似模型的=0917,=008121,的响应面近似模型的=0904,=007032。该精度检验结果表明该响应面模型可以较为准确的描述输出变量,与输入变量,,,,,之间的映射关系。

2)优化结果

自适应模拟退火算法是在传统模拟退火算法基础上提出的一种改进算法，分为内层和外层两个循环。外层循环用来控制温度在迭代过程中不断下降；内层循环在邻域附近进行扰动搜索(随机扰动采用柯西分布)，能够快速跳出局部最优点，改善了模拟退火算法中重复循环退火过程中优化效率低的缺点。优化过程中初始点随机选择，基本参数设置如表3所示。

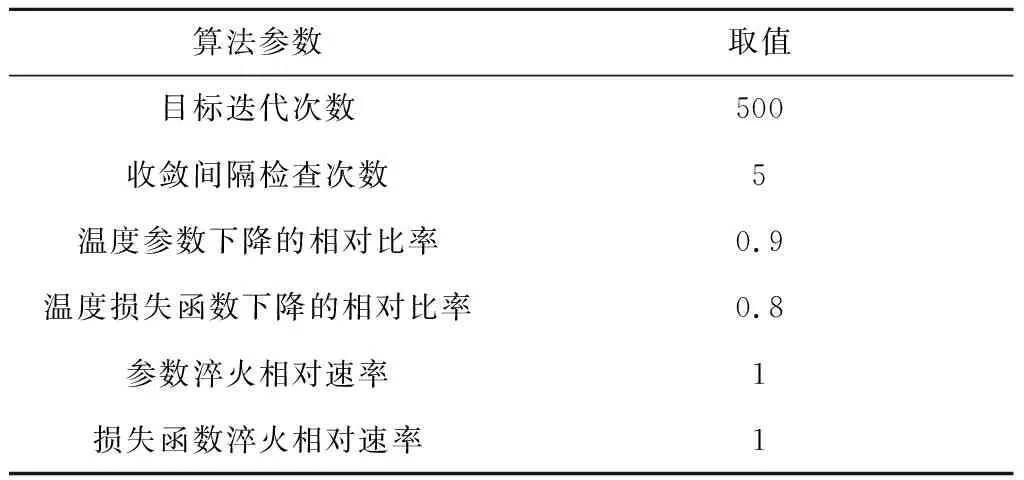
表3 ASA算法参数配置Table 3 ASA algorithm parameters configuration

优化程序一共运算了514步，最优解出现在第512步，目标函数迭代收敛历程如图11所示。设计变量最优解及对应的目标与约束取值如表4所示。

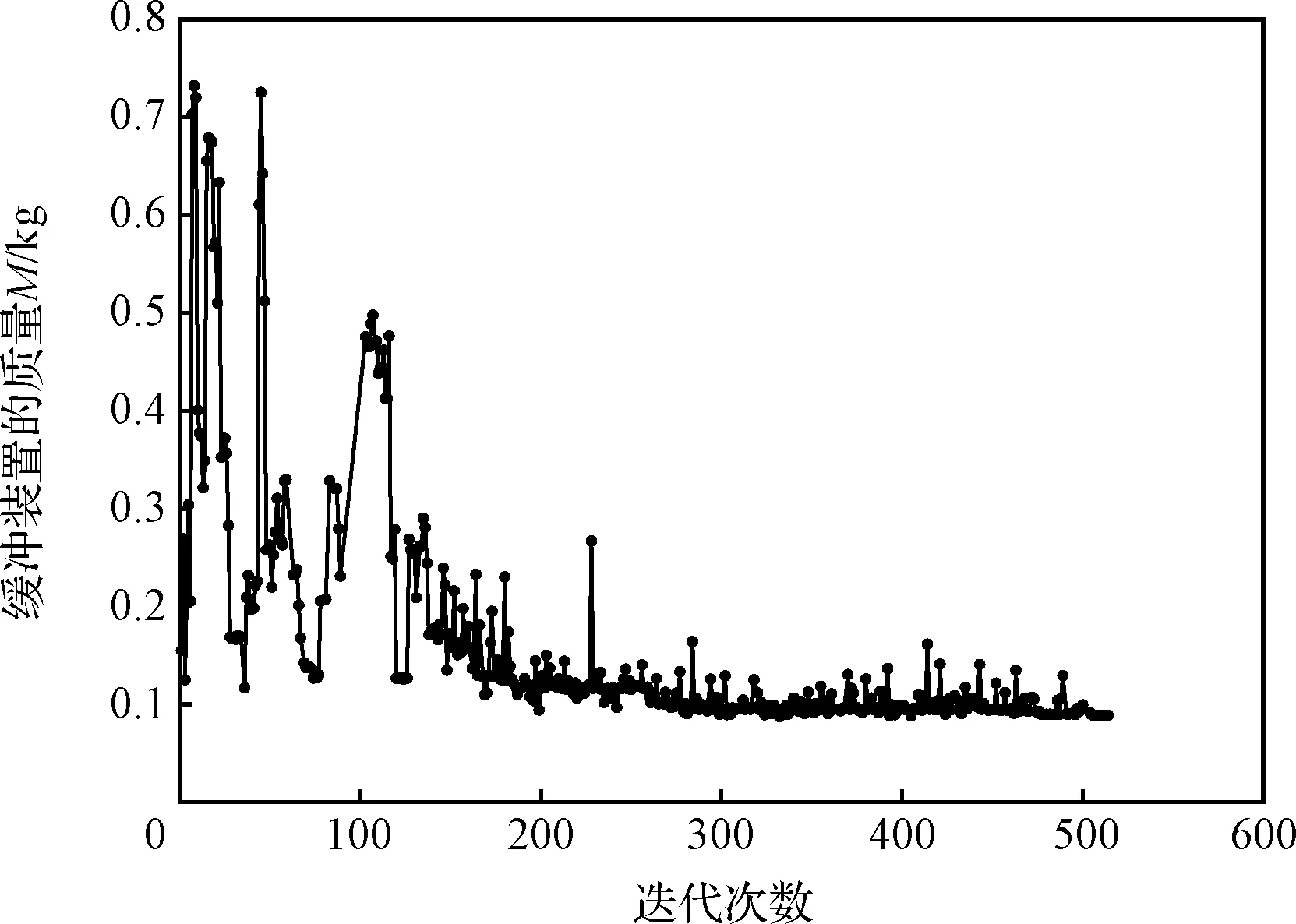
图11 目标函数迭代收敛曲线Fig.11 Iterative convergence curve of the objective function

图12～13显示了冲击激励在经过减冲击环前后的时间历程和冲击响应谱，可以直观看到明显的减冲击效果。

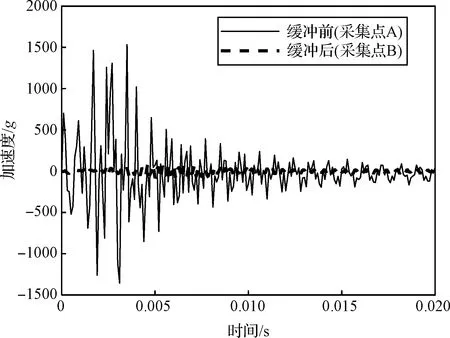
图12 A、B点的时域衰减曲线Fig.12 Time-domain attenuation curves of points A and B

表4中数据显示，优化后的重量为0.089 kg，相对于初始设计的0.119 kg，质量减轻了33.5%。设计变量层数最优解达到了下界2层，这有利于降低结构质量。此外，减冲击效果与强度约束都到达约束边界成为主动约束，而刚度约束还有一定的裕度。表4中数据提供的信息有限，难以据此深入认识结构性能，下节中将开展进一步的分析。

表4 设计变量最优解取值及对应的约束和目标值Table 4 Optimal solution values of design variables and corresponding constraints and target values

3.3 最优设计处敏度分析

为了更深入认识设计变量对减冲击环结构性能的影响，本小节在上文得到的最优点处开展质量、减冲效果、强度与刚度对6个设计变量的敏度分析评估。敏度本质上是在最优点处性能指标对设计变量的偏导数，本研究中采取数值差分的方法计算，以质量对支撑块高度的敏度为例，计算如式(23)所示：

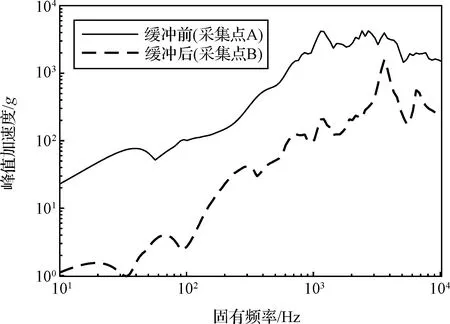
图13 A、B点冲击响应谱曲线Fig.13 Shock response spectrum curves of points A and B

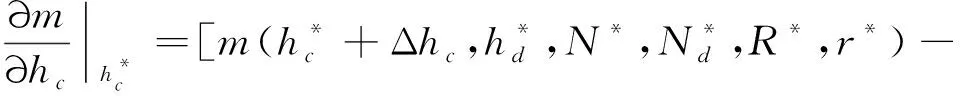
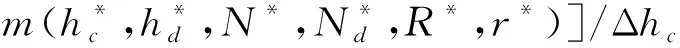
(23)

式中：Δ是在最优点处的扰动。实际计算中，扰动量取±1层，取±3块，,,,取对应最优解的±4%。按此方法计算得到的质量、减冲效果、强度和刚度对设计变量的敏度信息分别如表5～8所示。

表5中数据显示，对质量而言，减冲击环的层数是影响最敏感的设计变量；连续层厚度，环的内半径、外半径对质量的影响敏度与层数影响敏度的程度相当；支撑块的高度和数量对质量的影响敏度较小；,,,,与质量正相关，与质量负相关。

表5 最优点处减冲击环结构质量对设计变量的敏度值Table 5 Sensitivity values of the structural mass of the shock isolation ring to design variables

表6中数据显示，对减冲效果而言，减冲击环的层数也是影响敏度最大的设计变量；支撑块高度和数量的影响敏度与层数影响敏度量级相当；连续层厚度与内外径,的影响敏度较小。,,,与减冲效果正相关;,与减冲效果负相关。

表6 最优点处减冲效果对设计变量的敏度值Table 6 Sensitivity values of shock isolation effect to design variable

表7中数据显示，对强度而言，减冲击环的连续层厚度、内外半径,以及层数是敏度影响较大的设计变量；支撑块高度和支撑块个数对强度的敏度影响较小。,,与强度呈正相关;,,与强度负相关。

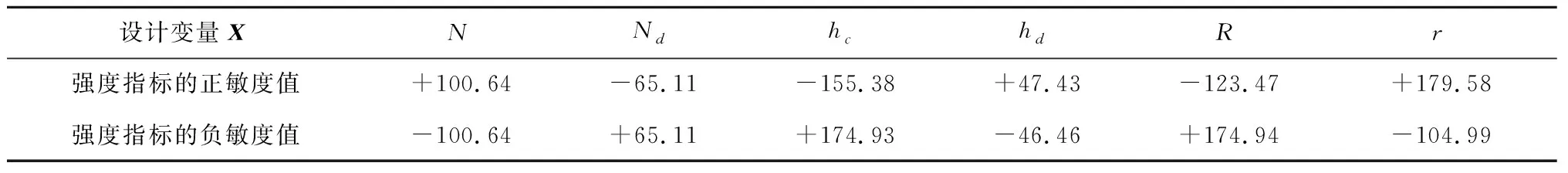
表7 最优点处强度指标对设计变量的敏度值Table 7 Sensitivity values of strength index to design variables

表8中数据显示，对刚度而言，减冲击环的层数是最敏感的设计变量，连续层厚度和支撑块个数影响敏度相当；内外半径,和支撑块高度对刚度的影响敏度较小。,,与刚度正相关;,与刚度负相关。

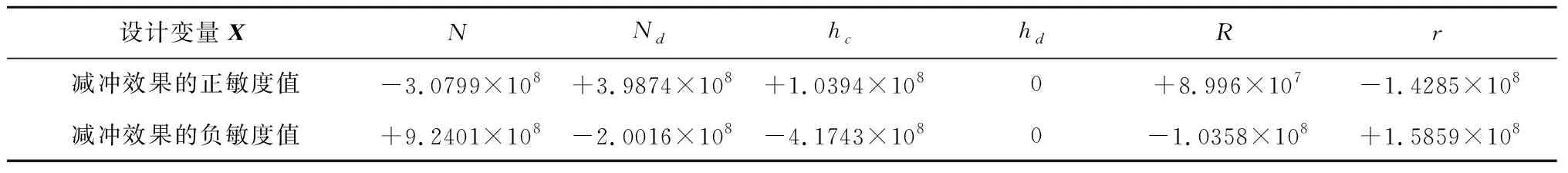
表8 最优点处刚度指标对设计变量的敏度值Table 8 Sensitivity values of stiffness index to design variables

综合上述分析，在6个设计变量中，减冲击环结构的层数是一个关键变量，对优化模型中所有结构性能都有明显影响。其次是支撑块数量，对刚度、减冲效果有明显影响。和是两个离散变量，也是减冲击环结构的两个明显的结构特征设计量，值得注意的是，它们对减冲效果与强度、刚度这三个重要的结构性能参数的影响敏度正好相反，在设计时需细致分析合理配置。

4 结 论

1) 采用冲击响应谱时域合成方法能计算得到符合冲击谱规范的时域载荷，即合成后时域载荷计算的冲击响应谱与标准谱的误差在±6 dB范围内，为星箭分离爆炸这类短时、强冲击工况下结构的分析和设计提供合理的载荷信息。

2) 减冲击环结构设计问题是一包含离散、连续变量的混合优化问题，自适应模拟退火算法能有效解决这类混合优化问题。优化后减冲击环质量相比初始结构减小了33.5%，结构的冲击响应谱最大值衰减了80%，结构强度到达设计边界，刚度还有一定裕度。

3) 本文构建的短时、强冲击载荷时域合成，优化设计与敏度分析整体计算框架对于其他短时、强冲击环境下的结构分析与设计具有参考意义。