机器人动态受力感知及零重力运动模拟技术

胡瑞钦，孟少华，张成立，董 悫，张立建

(1. 北京卫星环境工程研究所，北京 100094；2. 北京市航天产品智能装配技术与装备工程技术研究中心，北京 100094)

0 引 言

在轨服务(OOS)通常是指在太空中通过人、机器人或两者来延长航天器寿命或提高航天器能力的空间装配、维护和服务任务。为了使在轨服务系统适应微重力、真空、辐照等空间环境，在地面进行充分的试验验证是提高航天飞行成功率的有效措施。对于在轨服务技术的地面模拟试验，零重力模拟是其中的关键，也是其中的难点。目前，常用的失重模拟方法主要包括自由落体、抛物线飞行、气浮、水浮、悬吊和硬件在环(Hardware in loop，HIL)等方法，也有研究用磁性液体制造流体的超重、失重和微重力环境。

硬件在环方法采用原型样机与数学模型相结合的方式，是一种半物理仿真方法，可用于空间机构的地面零重力模拟试验，如对载人航天器的在轨对接进行地面模拟。这种方法需要实时精确测量模拟对象的受力，而后借助动力学模型计算对象在零重力环境下的运动速度，然后由机器人实现相应的运动。其中，精确的受力感知是实现准确运动模拟的前提。

对于机器人末端负载的零重力运动实现，现有技术主要包括两种方法。

一种方法是对机器人进行零力控制，需要预先辨识机器人各部分的质量特性，建立机器人的动力学模型，实现机器人运动过程中关节力矩的预测。在机器人运行过程中实时采集关节力矩，将实际关节力矩与预测力矩进行比较，得到机器人受外力的情况，并驱动机器人实现零重力运动。该方法不需要为机器人额外增加传感器，但该方法的一个重要问题是无法准确测量或预测关节摩擦力矩，对于大负载机器人，难以实现精确的受力感知。这种方法通常应用于轻载机器人的拖动示教。

另一种方法是在机器人腕部安装六维力传感器。六维力传感器可以精确测量空间任意力系中的三维正交力(,,)和三维正交力矩(,,)。对于重载机器人，它仍然可以获得较高的测量分辨率，从而能够实现更准确的零重力运动模拟。

如图1所示，在机器人执行任务的动态调整过程中，机器人腕部六维力传感器测得的力与力矩数据由四部分造成，即:1)传感器本身的系统误差，2)负载重力效应，3)负载的惯性力和惯性矩，4)外部接触力。

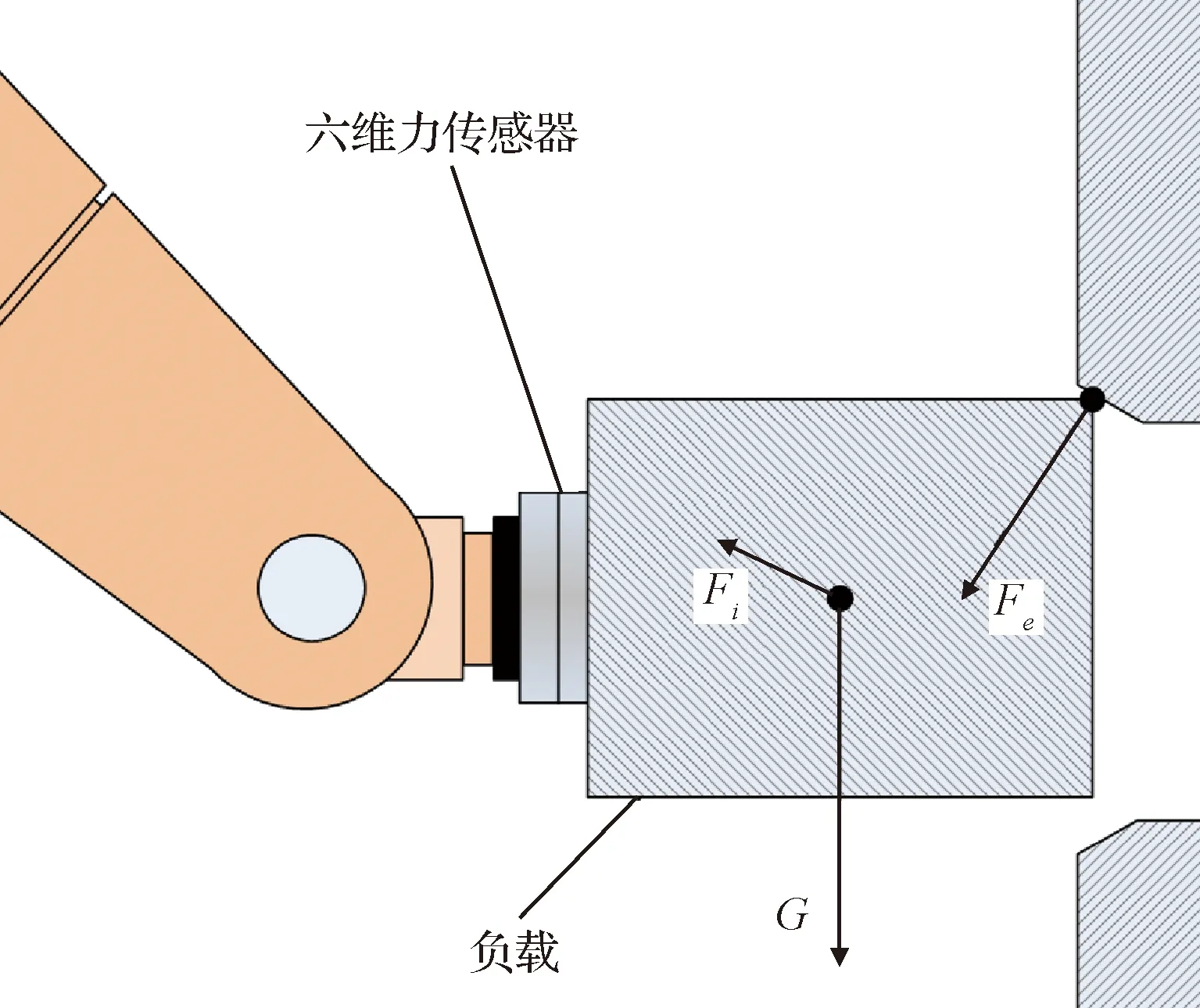
图1 机器人末端负载受力情况示意图Fig.1 Scheme of the forces on the end load of the robot

为了获得外部接触力信息，必须消除六维力传感器数据中传感器系统误差、负载重力、负载惯性力和力矩的影响。当负载重量较小时，负载重力和惯性力的影响可以忽略。当负载重量较大，但机器人运动的动态程度较低、加速度较小时，应考虑重力的影响，而惯性力的影响可以忽略。当负载重量较大，机器人运动动态程度较高时，必须考虑负载重力和惯性力的影响。

本文主要研究使用机器人模拟物体的失重运动。由于负载重量大、运动动态程度高、运动范围大，需要在机器人的整个工作空间中准确地感知负载的受力，必须考虑负载惯性力的影响。

在已有研究中，机器人末端的受力感知模型通常采用解析方法建立，即考虑影响力感知各因素之间的物理关系，推导出外部接触力与各已知量之间的数学模型。然而，影响力感知的因素较多，包括机器人底座安装角度、传感器在机器人上的安装角度、机器人的位置和姿态反馈误差等。使用解析方法很难考虑所有这些因素，而一些因素往往在建模中不得不被忽略，使得建模过程能够向下进行，这不可避免地带来误差。

近年来，随着计算机计算能力的提高，机器学习、人工智能等技术应运而生。对于影响因素复杂且无法进行显式建模的情况，可以通过采集数据样本和迭代优化得到最优模型。这种方式不需要关心模型的具体参数，可以获得较高的预测精度。

目前，已有研究利用机器学习进行机器人末端的受力感知。Yao等通过神经网络建立六维力传感器的误差模型，消除传感器本身的测量误差。Su等建立一个神经网络模型，根据机器人反馈的末端姿态数据预测六维力传感器数据中的负载重力分量，从而消除负载重力的影响。Kim等使用惯性测量单元(IMU)测量机器人末端的姿态，建立了负载重力分量与负载姿态角的神经网络模型，并实现了由姿态角对负载重力分量的预测。在该方法中，姿态角的反馈及负载重力影响的补偿与机器人本身无关。Lin等研究动态条件下机器人的力感知问题，使用BP神经网络通过机器人关节角度预测负载重力的影响，并进一步使用解析方法计算惯性力/力矩的影响，以实现机器人末端的动态受力感知。Dine等使用递归神经网络(RNN)，采用机器人末端姿态和IMU反馈数据作为输入，预测机器人末端的受力。

针对传统解析法难以考虑全部因素并进行精确建模的问题，本文采用机器学习方法实现机器人整个工作空间内负载的力觉感知。研究中采用BP神经网络，以机器人末端位置和姿态数据、IMU反馈的加速度和角速度数据以及对角速度数据差分得到的角加速度数据作为输入层参数，以六维力传感器在负载不受外力作用时的输出作为输出层参数。与已有研究相比，本研究在输入层引入了IMU角速度数据差分获得的角加速度信息，这是由于经过力学理论分析，负载旋转引起的惯性力矩与其角加速度直接相关，角加速度信息的引入有助于获得更高的预测精度。另一方面，本研究将机器人末端的位置和姿态信息作为输入层参数的一部分，在采样时尽可能覆盖机器人的整个工作空间，使训练后的模型能够在机器人的整个工作空间内获得较高的精度，满足零重力运动的大范围运动要求。

1 机器人末端负载受力分析

对于图1所示的机器人末端负载，其受到的外部作用力与力矩为

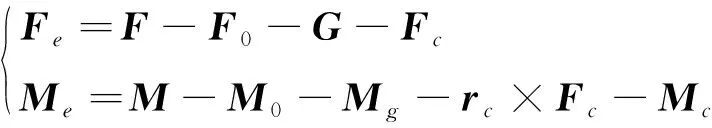
(1)

其中,,为六维力传感器的力与力矩读数;,为六维力传感器自身的系统误差;,为负载重力及重力带来的力矩;为负载惯性力，可通过负载质量与测得的负载加速度计算得到；为负载质心在六维力传感器坐标系中的坐标向量;×为负载惯性力引起的力矩;为负载转动带来的惯性力矩。

传感器的系统误差,为常量，易通过静态标定得到。对于负载重力及重力带来的力矩,，需要考虑负载重力大小、方向、及质心在六维力传感器坐标系中的坐标。假设负载重力大小为，重力方向与六维力传感器坐标系,,轴间的夹角为,,，则可计算得到负载重力在六维力传感器坐标系3个坐标轴上的投影为

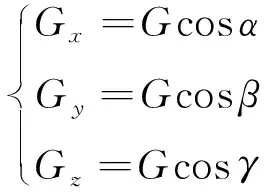
(2)

假设负载质心在六维力传感器坐标系中的坐标为(,,),负载重力对,,轴的作用力矩分量分别为

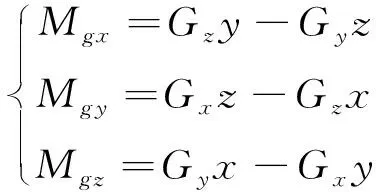
(3)

在机器人运动过程中，由于重力方向始终竖直向下，重力方向与六维力传感器坐标系,,轴间的夹角,,也随机器人的运动而实时变化，因此，计算重力影响分量需要实时采集机器人末端姿态数据。

对于负载惯性力，根据牛顿第二定律，负载惯性力为

=-m

(4)

其中,表示负载质量，为负载质心位置的运动加速度。

对于负载转动带来的惯性力矩，根据欧拉公式得到

(5)

基于以上分析，采用传统解析方式进行机器人末端动态受力感知，需要建立在以下数据的基础上：

(1)常量数据：①六维力传感器测量系统误差；②机器人底座安装角度、传感器在机器人上的安装角度；③负载质量大小、质心在六维力传感器坐标系中的坐标；④负载惯性张量。

(2)变量数据：①六维力传感器读数；②机器人末端实时位姿；③负载运动的加速度、角速度、角加速度。

对于上述变量数据，六维力传感器读数由六维力传感器直接得到。机器人末端实时位姿可以由机器人控制系统实时得到，对于串联式的工业机器人，由于其结构特点，机器人反馈的末端位姿往往存在较大误差。而负载运动的加速度、角速度、角加速度可以由机器人的位姿、速度反馈换算得到，也可以借助惯性测量单元(IMU)等传感器测量得到。

对于上述常量数据，机器人底座安装角度、传感器在机器人上的安装角度需要提前进行测量标定，或通过机械定位确保安装精度。其余常量也需要提前进行辨识，而对于负载惯性张量，难以进行精确的辨识。常量数据的误差将影响最终的受力感知误差。

若采用传统解析方式，需要提前对上述常量进行精确标定，并在机器人运动过程中对上述变量进行精确采集。而由于部分常量(如惯性张量)难以精确测定，部分变量(如机器人末端位姿)的误差较大且难以进行精确测定补偿，使得使用传统解析方法难以满足机器人在大负载、高动态、大运动范围条件下的精确受力感知需求。

若采用机器学习方式，则在负载不受外力的情况下直接采集上述变量样本数据。将六维力传感器的数据作为输出，其他变量作为输入。由于机器人末端不受外力作用，每组样本输入对应的输出预测值应等于六维力传感器的测量值。通过采集机器人在整个工作空间内不同运动状态下的数据样本，对机器学习模型进行迭代训练，得到末端力的预测模型。当机器人末端受到外力作用时，利用六维力传感器的实际测量值减去机器学习模型的预测值即可获得外力信息，从而实现对负载的受力感知。这种方式无需对上述常量进行预先标定，对于难以进行解析建模的非线性误差(如机器人末端位姿误差)也可以进行精确的拟合，能够满足所述应用需求。

2 基于机器学习的力传感器输出预测模型

本研究采用BP神经网络建立受力预测模型。BP神经网络具有很强的非线性映射能力，适合于本研究中的受力预测。神经网络的结构如图2所示。在输入层，使用来自机器人控制器的位置和姿态数据、IMU测量的加速度和角速度数据以及对角速度差分得到的角加速度数据。输出层是预测的六维力传感器数据。输入层与输出层间采用单层隐藏层，隐藏层的节点数需要根据试验确定，既要对样本数据获得较低的预测误差，又要避免“过拟合”，神经元的激活函数采用Sigmod函数。

图2 机器人末端受力预测神经网络模型Fig.2 The structure of force prediction neural network for the end load of the robot

为训练该神经网络，使机器人在末端不受外界作用的情况下进行运动，在此过程中采集输入层对应数据，并以同一时刻六维力传感器采集的数据作为此时输入数据对应理想输出值，由此得到输入层与输出层的样本数据。利用这些数据对所述神经网络进行训练，得到机器人负载不受外力条件下的六维力传感器输出预测模型。

利用该模型可以预测在机器人末端不受外界作用条件下的六维力传感器输出值，当机器人末端受到外界作用力时，用六维力传感器实际测量值减去预测值，即可得到外界作用力信息，实现对机器人末端负载的受力感知。

3 受力感知试验研究

3.1 试验系统

试验系统组成如图3所示，在机器人腕部安装六维力传感器，并在机器人末端安装惯性测量单元。机器人采用KUKA公司的KR210机器人，其主要参数见表1。六维力传感器采用ATI公司的Omega191型传感器，其测量范围及分辨率参数见表2，其中(,,)表示三维正交力的测量值，(,,)表示三维正交力矩的测量值。惯性测量单元采用Sensonor公司的STIM300惯性测量单元，该传感器采用三个高精度的MEMS陀螺和MEMS加速度计分别对,,轴向的角速度和加速度数据进行测量，主要技术参数见表3。

表1 KR210机器人性能参数Table 1 Performance parameters of the robot KR210

表2 六维力传感器Omega191技术参数Table 2 Technical parameters of Omega191 F/T sensor

表3 惯性测量单元STIM300技术参数Table 3 Technical parameters of STIM300 IMU

图3 机器人末端动态受力感知试验系统组成Fig.3 Components of the force perception test system of the robot end

惯性测量单元可以直接测得运动的加速度和角速度，由前述理论分析可知，计算机器人末端负载载惯性力矩还与其运动的角加速度直接相关，为此，对惯性测量单元的角速度数据序列进行差分得到角加速度数据。

试验系统实物如图4所示，惯性测量单元安装在机器人末端与六维力传感器之间的转接件内，使得系统在实际应用中更为紧凑，避免在机器人运动中产生额外的干涉，试验用机器人负载重量为100 kg。

图4 机器人末端动态受力感知试验实物Fig.4 Photograph of the force perception test system of the robot end

3.2 样本数据采集

为了使样本数据能够尽可能覆盖机器人的全工作空间，又能够减少样本总量，提高模型训练的效率，研究中采用了正交试验设计方法。对机器人的6个旋转轴A～A，在各自的转动范围内均匀地取10个角度值，取值时可能覆盖整个运动范围，同时考虑在运动中机器人末端负载不会与机器人自身或周围物体发生干涉，各轴取值范围情况见表4。按照正交试验设计的思路，将A～A轴的角度值作为试验的6个因素，并将每个轴的角度值按照各自的运动范围平均分为10个水平，按照L(10)正交表安排试验中机器人运动路径点各轴角度的取值。

表4 试验中机器人各轴转动范围Table 4 Rotation ranges of each axis of the robot in the experiment

机器人按照正交表所列的路径点顺序运动，从当前点运动至下个路径点采用点到点(PTP)的运动方式，并在每个路径点停留2 s，这样机器人的运动包含了加速、减速、静止的过程。考虑到机器人在应用中的实际速度，限定机器人的运行速度为自动模式最高额定速度的30%。在机器人运动过程中，以12 ms的周期同步采集机器人末端位姿参数、六维力传感器数据、惯性测量单元数据。

试验中采集的部分样本数据见图5～8。从图中可以看出，样本采集时间约15 min，样本数据平滑连续。其中,图5为从机器人控制器获取的机器人末端位置数据，图6为从惯性测量单元读取的加速度数据,图7为由惯性测量单元角速度数据差分得到的角加速度数据，波动较为剧烈,图8为从六维力传感器读取的三维力数据。此外，采集的样本数据中还包括机器人末端姿态数据、惯性测量单元的角速度数据，及六维力传感器的三维力矩数据，由于篇幅有限，未在文中列出。

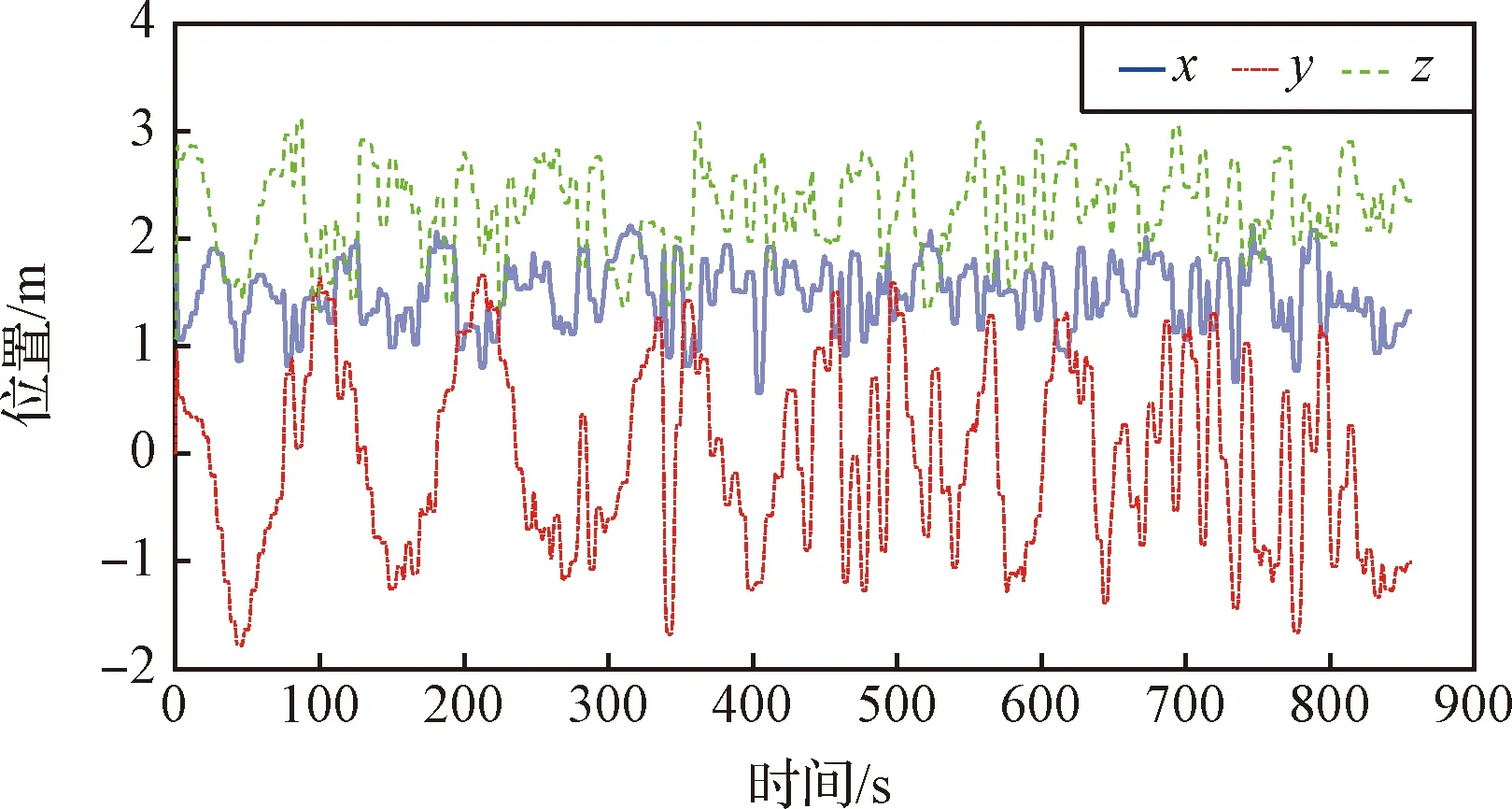
图5 机器人末端位置数据曲线Fig.5 The curves of the position data of the robot end

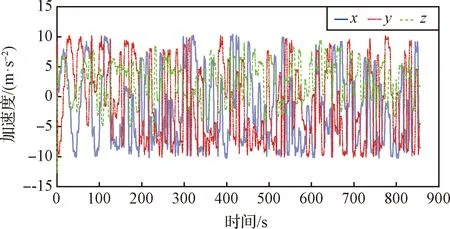
图6 机器人末端加速度数据曲线Fig.6 The curves of the acceleration data of the robot end

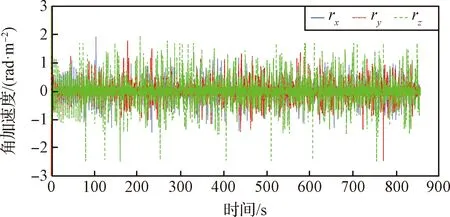
图7 机器人末端角加速度数据曲线Fig.7 The curves of the angular acceleration data of the robot end

图8 机器人末端力数据曲线Fig.8 The curves of the force data of the robot end

3.3 模型训练

研究中采用梯度下降法对图2所示的神经网络进行训练，图2的神经网络采用了单层隐藏层，隐藏层的节点数还需要确定。在BP神经网络中，隐藏层节点数对建立的神经网络模型的性能影响很大，而且是出现“过拟合”的直接原因。研究中为尽可能避免训练时出现“过拟合”现象，保证足够高的网络性能和泛化能力，在满足精度要求的前提下取尽可能紧凑的结构，即取尽可能少的隐层节点数。

训练中将数据样本分为训练集(train)、验证集(validation)和测试集(test)，训练集占样本总数的60%，验证集与测试集分别占20%，3个子集数据随机选取。其中训练集用来训练模型，验证集用来评估模型预测的好坏及调整对应的参数，测试集用于测试已训练好的模型对于新数据的泛化能力。

为确定神经网络中隐藏层节点的数量，使用不同数量的隐藏层节点进行训练，每个数量的隐藏层节点重复训练3次，每个隐层节点3次训练得到的均方误差用于评估相应隐层节点数下的预测精度，并记录不同隐层点数下的单次迭代计算时间。不同隐层节点数下的预测精度及运算时间比较如图9所示。根据试验结果，考虑到训练时间和精度要求，同时为避免过拟合，在满足精度要求的前提下尽量使模型简单，选择较少的隐层节点数，本研究确定隐层节点数为8个。

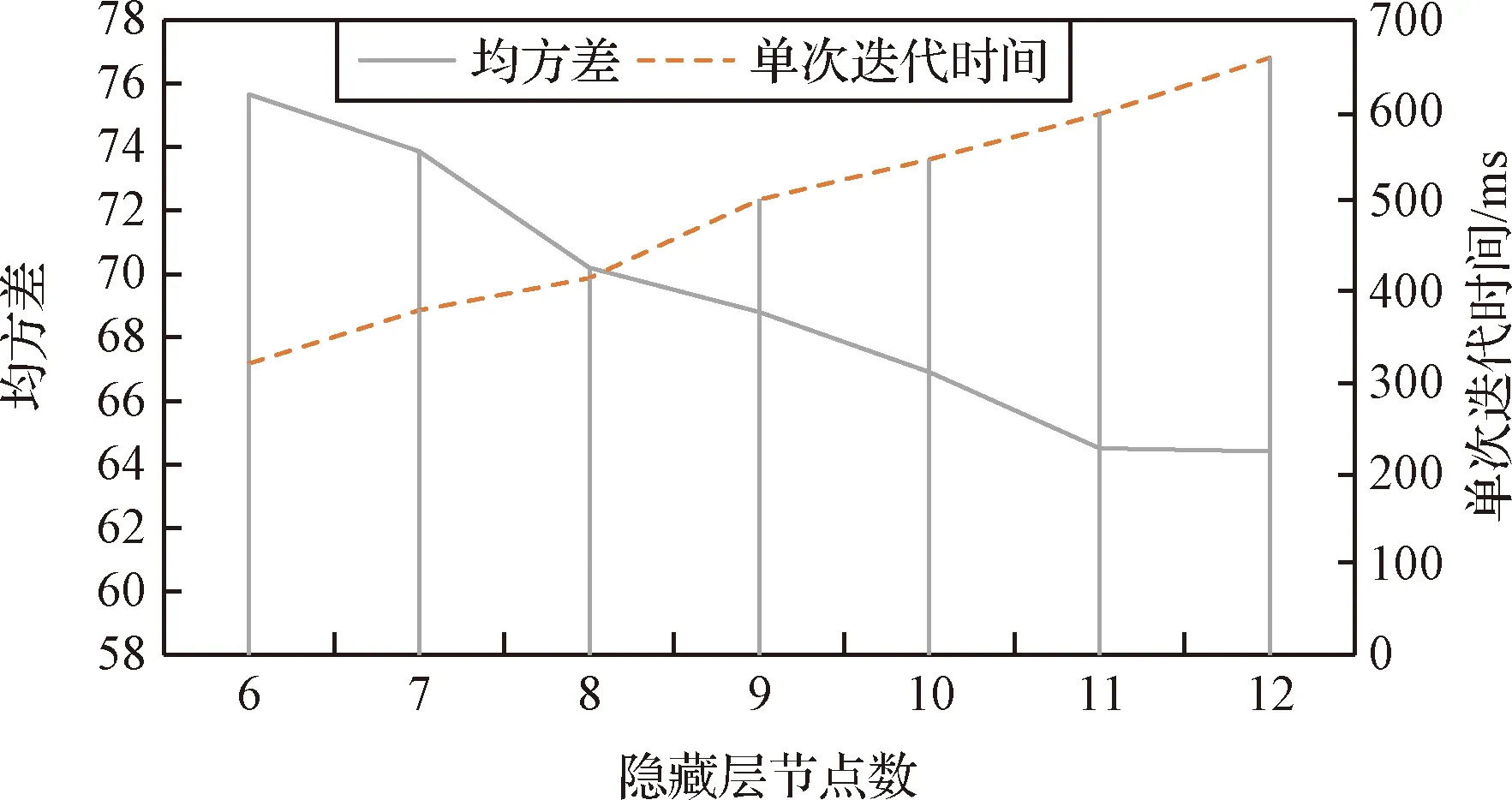
图9 不同隐藏层节点数下的预测精度对比Fig.9 Prediction accuracy under different hidden layer nodes

3.4 模型预测精度试验结果

对于图4所示的系统，在机器人运动过程中实时采集机器人末端位姿数据、六维力传感器数据、惯性测量单元数据，并输入已经训练好的受力感知模型中，可实时计算得到预测的六维力传感器数值，将六维力实际测量值减去预测值，可得到预测误差。

取连续10 s时间的机器人运动过程，对比六维力传感器实测数据与模型预测数据，并给出相应的误差，代表性的结果如图10～11所示。图中在1～3 s的时间范围内，机器人处于静止状态，在其余时间机器人处于运动状态，因此，选取的相关数据包含了机器人静态与动态过程。由图可见，与静态情况相比,机器人在动态条件的预测误差更大。

图10 X方向力数据预测误差Fig.10 Force prediction error in direction X

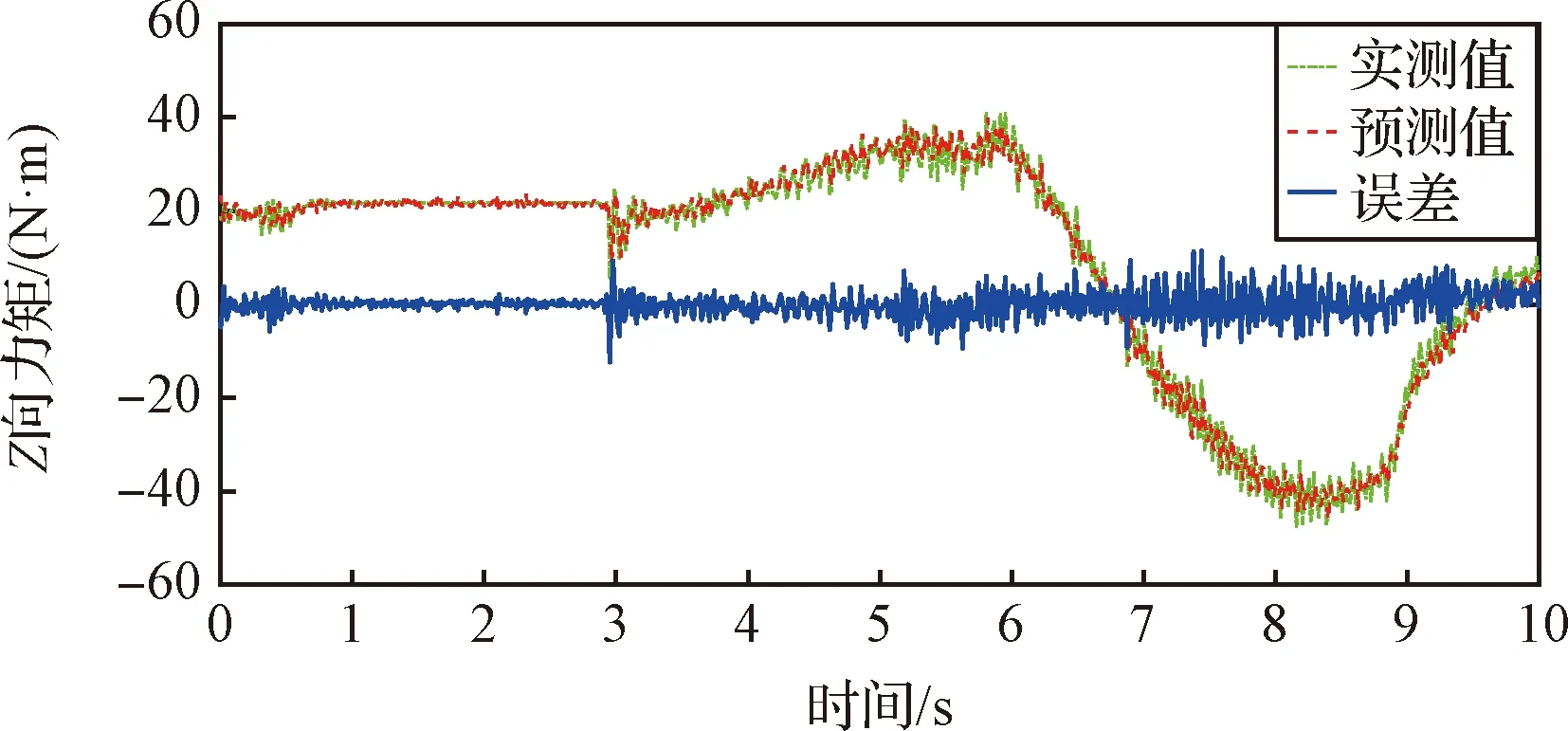
图11 Z方向力矩数据预测误差Fig.11 Torque prediction error in direction Z

对于实测数据与模型预测数据的误差数据，计算每个分量的最大误差和均方根误差，以评估预测误差，见表5。结果表明，力感知的最大误差为39.8 N，均方根误差为9.3 N；力矩感知的最大误差为18.7 N·m，均方根误差为4.4 N·m。在表5中同时列出了各分量实测记录数据中的最大值作为参考，用以说明得出的感知误差所对应的分量取值范围，以评价模型预测的效果。

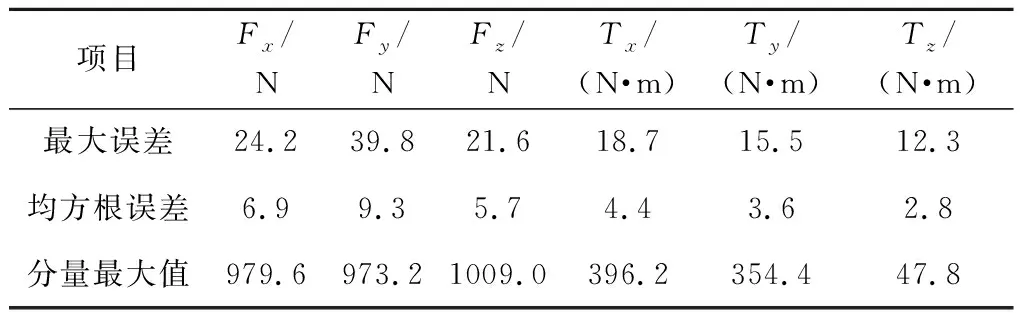
表5 动态受力感知误差统计Table 5 Error statistics for the dynamic force perception

由图10～11可知，误差较大的情况出现在机器人运动过程中，这是由于动态条件下，六维力传感器、惯性测量单元的波动更为剧烈，对传感器数据或对最终的受力感知数据进行滤波处理，可进一步降低误差。

4 零重力运动模拟实现

根据牛顿第二定律和欧拉方程，得出关系式

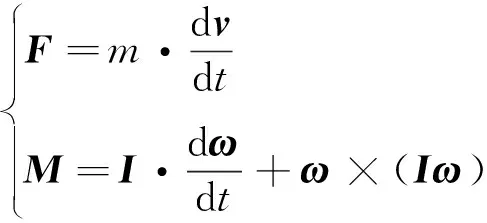
(6)

其中,为机器人负载的质量,为负载质心的运动速度,为负载的惯性张量，进一步推导得到

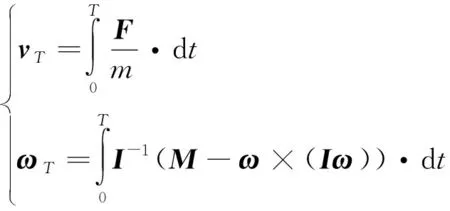
(7)

式中:,为时刻负载运动的速度、角速度,即机器人在时刻的运动速度，可根据时刻之前采集的受力及角速度信息积分计算得到。其中机器人末端的负载受力信息可由前述的受力感知模型实时得到，再由式(7)计算得到负载运动的速度，并驱动机器人按照相应的速度运动，即可实现对负载的零重力运动模拟。

由式(7)，由于采用对以往数据积分的形式计算机器人当前运动速度，在零重力模拟中，上述机器人在运动条件下受力感知数据的实时波动，被积分“吸收”，并不会造成机器人运动的剧烈波动。

式(7)中，与的取值可以按照机器人末端负载的实际质量及惯性张量取值，也可以指定为其他希望被模拟的数值，实现“半物理仿真”，虽然机器人末端负载的质量特性与希望模拟的对象不同，但可以通过数字指定质量特性的方式，实现对模拟对象的等效运动仿真。

对图4中的机器人末端负载进行零重力运动模拟，试验者用手作用于机器人末端负载，可以使试验者在地面环境下获得对物体零重力“漂浮”状况的体验。

5 空间站在轨装配地面模拟试验应用实例

空间站某型号天线重约60 kg，需要在轨由航天员进行安装，天线在轨出现故障时，也需要由航天员在轨进行更换。为评价该型号天线在轨操作任务的可行性及人机功效，需要在地面模拟在轨安装情况，使天线处于零重力状态，由试验人员按照在轨操作流程进行操作，通过试验检验相关操作流程能否顺利进行，并记录试验人员的操作施力大小，以评价操作的费力程度，判断操作需要的力是否在航天员在轨正常可施力的范围内。

针对该型号天线的在轨模拟试验需求，制作与真实天线外形、接口一致的模拟件，并在模拟件上设计与机器人末端连接的接口。在模拟件与机器人完成连接后，首先按照前述样本采集过程采集得到样本数据，接着对所述神经网络进行训练，获得机器人末端力感知模型，而后按照前述零重力运动模拟方法实现对模拟件的零重力模拟。相关技术已成功应用于空间站某型号天线的在轨安装地面模拟试验中。

图12 在轨操作零重力模拟应用照片Fig.12 Photograph of the zero-gravity simulation for on-orbit operations

对于部件的零重力模拟，常用的传统方法包括悬吊、气浮、水浮等方法，与这些方法相比，使用机器人进行零重力模拟的优点在于：

1) 装置简单，布置灵活，仅需要一台机器人即可完成模拟任务，若机器人下方配置移动平台，还可以灵活移动至不同位置使用；

2) 可以实现三维空间6个自由度的运动模拟；

3) 可实现半物理仿真，仅需要模拟件具有与真实件一致的外形，而不需要其具有与真实件同样的质量特性，可以节省成本，简化模拟过程。

采用水浮方法也可实现6自由度的运动模拟，也有研究通过特殊设计的机构基于气浮方法实现多自由度的运动模拟，但系统配置及使用过程较为复杂，难以实现快速、灵活的应用。

6 结 论

本文针对航天器在轨服务任务地面零重力模拟的需求，研究使用工业机器人实现部件的零重力模拟。采用BP神经网络建立受力感知预测模型，实现机器人在全工作空间的动态受力感知。试验系统中，采用六维力传感器测量机器人腕部受力，并采用惯性测量单元测量机器人末端的加速度、角速度，通过差分方式获得机器人末端的角加速度。应用正交试验设计方法确定机器人数据采集路径。研究采用试验方法确定神经网络隐藏层的节点数，兼顾模型的逼近能力和泛化能力。应用训练得到的神经网络模型进行机器人末端负载的受力感知计算，对于100 kg的机器人末端负载，试验获得力感知的最大误差为39.8 N，均方根误差为9.3 N，力矩感知的最大误差为18.7 N·m，均方根误差为4.4 N·m。

应用所述受力感知技术，结合运动学理论，实时计算得到机器人末端负载运动的速度，并驱动机器人按照相应的速度运动，实现了对机器人末端负载的零重力运动模拟。相关成果成功应用于空间站某型号天线在轨安装的地面模拟试验中，为航天器在轨任务的地面零重力模拟提供了一种基于工业机器人的解决方案。

后续对于系统的零重力模拟应用，在高频冲击响应控制方面有待进一步开展研究，实现系统对零重力条件下碰撞等高频冲击情况的准确模拟。