空间旋转目标涡流消旋概念与仿真分析

石永康，杨乐平，朱彦伟，褚福东

(国防科技大学太空安全战略研究中心， 长沙 410073)

0 引 言

地球轨道空间存在大量失效卫星和碎片，一方面这些失效卫星和碎片占据在轨道上，浪费了原本就十分有限的空间资源；另一方面，这些非合作目标存在与其它在轨卫星发生碰撞的风险，严重威胁现有卫星的安全运行[1]，所以必须对这些失效卫星和碎片实施维修、回收或清除。然而，处于漂浮状态的失效卫星或碎片，一般是旋转或翻滚的。

现有空间操控手段如机械臂[2]、空间绳网[3]等大多需与操作目标发生物理接触，且要求相对速度很小或相对静止，否则会发生强烈的碰撞[4]，所以接触式的操作手段只适用于转速很小的目标。通过观测发现，失效卫星或碎片实际的旋转速度[5]可以高达180(°)/s，远远超出了接触式操控手段所容许的范围。因此，采取非接触式的消旋手段是十分必要的。

涡流消旋是基于电磁—涡流阻尼效应的制动方法，它是利用感生涡流产生的电磁力矩，作用在目标星上形成阻尼效应，从而实现消旋。航天器涡流消旋的想法起源于涡流力矩[5]，而涡流力矩的理论依据是楞次定律。初期，研究人员通过在轨实验测量了涡流力矩的大小，并试图利用这种在地磁场中自然形成的涡流力矩来进行航天器的姿态控制，但这种涡流力矩十分微小，并不具备可用性，航天器涡流力矩的研究也因此被一度中断。到二十世纪八十年代，有科学家[6]提出使用通电线圈或永磁铁等常规磁体来产生较大涡流力矩，研究了涡流力矩作用下航天器的姿态控制[7]，并正式提出了常规磁体涡流消旋的概念。航天器涡流消旋比较系统的研究是从美国科学家Kadaba等的科研工作[7-8]开始的，他们研究了涡流力矩对失效卫星的消旋作用，并讨论了常规磁体涡流消旋的工程可行性[8]。随后，日本的Sugai等[9]也研究了涡流消旋技术，他们利用涡流力矩对大型空间碎片进行消旋，研究了涡流消旋的基本理论、涡流消旋的策略等，并进行了基本原理的仿真和地面试验[10]。但是，他们所设计的试验系统与真实航天器涡流消旋存在较大差别，譬如涡流制动器与目标之间的距离假设很小。最近五年以来，由于空间碎片清除及在轨服务的迫切需要，涡流消旋重新获得了研究者的关注，其中，最为突出的是南安普敦大学的研究团队[11]，他们采用超导线圈来产生强大的电磁场[11]，目前已完成了涡流消旋机理，涡流力/力矩模型等的研究，开展了仿真实例分析，设计了地面试验平台[12]，然而，他们并没有明确阐述超导磁体涡流消旋的概念内涵，也没有说明使用超导磁体后消旋技术的优势及可行性。此外，德国人工智能研究中心也开展了相应的研究[11]，并参与了欧空局的“Agora mission”项目，将演示Ariane火箭上面级的自主式涡流消旋、捕获及离轨。国内对涡流消旋的研究尚处于启动阶段，仅有极少科研院校关注了该项技术。

综上所述，航天器涡流消旋的概念从提出到现在，已经有三十多年的历史，但一直以来，都没能引起广泛的研究兴趣，主要原因仍然是涡流力矩不够强大。电磁—涡流阻尼的作用强度是否能有效支持航天器消旋任务的开展是必须首先解决的问题。本文将第二代高温超导技术与非接触涡流制动技术相结合，提出超导式涡流消旋的概念，由于超导材料能支持几十倍于常导材料的电流，超导式涡流消旋将具有更强的消旋能力和更远的作用距离。

1 超导式涡流消旋的概念与内涵

1.1 涡流消旋的概念设计

考虑到涡流消旋操作过程中，需要将服务星上的消旋装置保持在离目标星一定的距离处，且恒定地指向目标星。服务星的总体构造采用连杆机构将超导电磁线圈与卫星平台连接起来的形式，具体结构形式如图1所示。图1中，圆形的大线圈通过转动副与二连杆机构的末端相连，从而可实现电磁线圈一定角度范围内指向的调整；服务星通过调节二连杆机构，实现消旋装置的收放，并辅助调节消旋装置与目标星之间的相对距离。

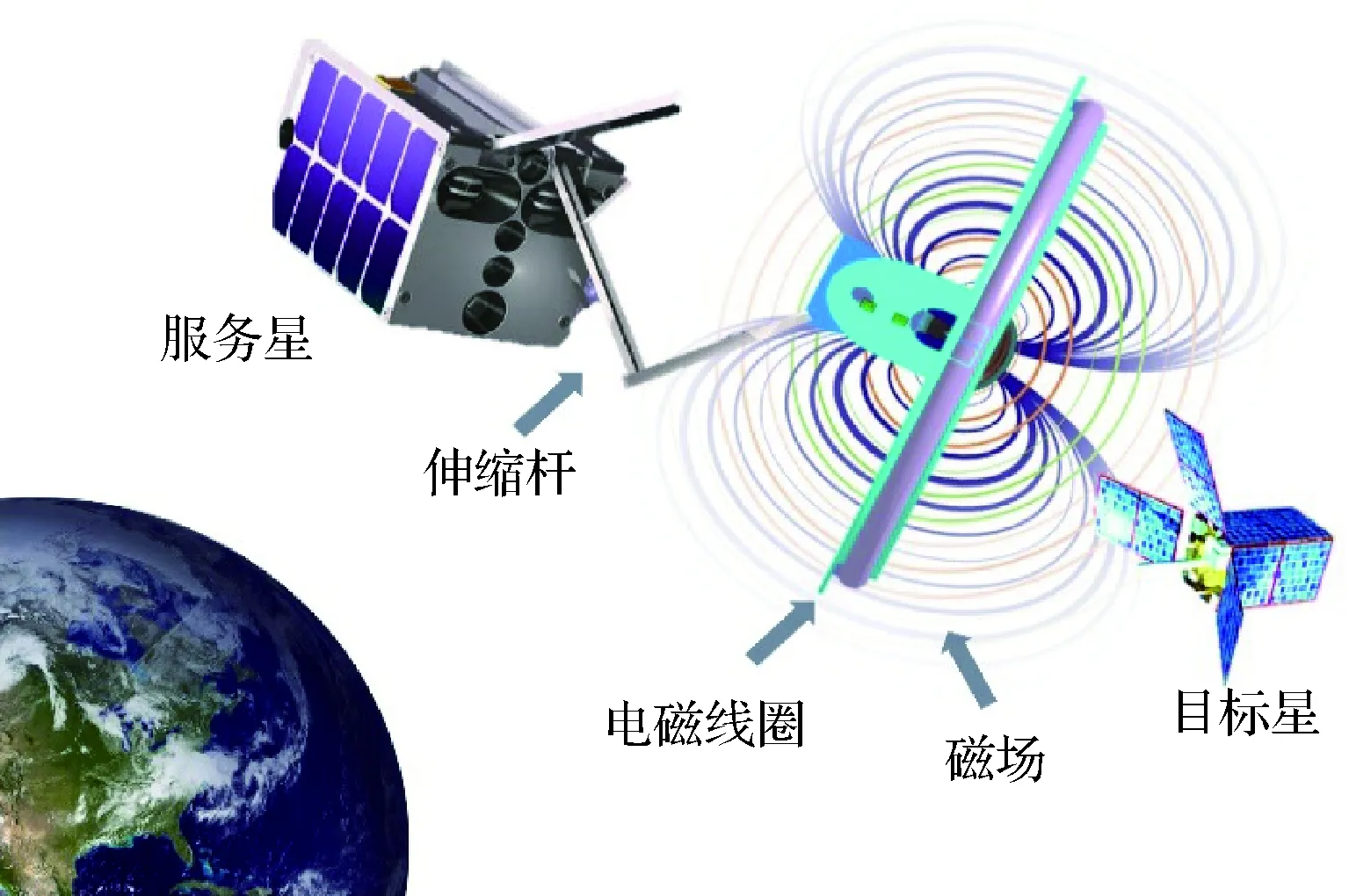
图1 服务星构造及对目标星实施消旋的概念示意图Fig.1 Structure of chaser spacecraft and schematic diagram for achaser spacecraft to despin a target spacecraft

1.2 涡流消旋的机理分析

根据电磁学理论，对航天器涡流消旋中的电场、磁场、电磁力/力矩进行分析，可得涡流消旋过程中电、磁、力等物理要素之间的作用关系为：旋转的目标星在激励磁场(见图2中激励磁场的磁力线)的作用下感应出涡流；根据楞次定律，感应涡流的效果总是阻碍引起感应涡流的原因，也就是说，涡电流(见图2中环形电流)所生成的磁场与原激励磁场之间始终是相抵制的，表现为对旋转运动的电磁阻尼效应。航天器涡流消旋就是利用这种相互抵制的电磁阻尼来对目标星消旋的。消旋过程中，服务星与目标星组成了一个双星编队，两星相对转速在涡流力矩的作用下逐步变慢，直到编队的相对转动完全消失为止，涡流消旋的阻尼作用才终止。

图2 航天器涡流消旋的作用机理图Fig.2 Action mechanisms of eddy brake on space object

由上述分析可知，涡流消旋是由于存在相对转动而产生的一种实时交互的、多物理场耦合的作用，它与磁场感应强度及其分布、相对距离及相对转动、目标星形状和材料的导电性能等有关，同时，还受到地球磁场等环境因素的影响，是一种极其复杂的作用关系、某些作用特性尚待进一步探索。

2 超导式涡流消旋概念的定性分析

通过综合比较多种消旋手段，本节从工程应用的顶层定性分析涡流消旋的技术优势及其可行性。

2.1 现有消旋方法的比较分析。

科学家针对不同空间目标提出了不同的消旋方法[13- 14]，这些消旋方法按是否与目标发生触碰可归纳为两大类：接触式和非接触式消旋方法。接触式消旋方法有机械臂消旋、减速刷消旋等。非接触式消旋方法有射流消旋、静电力消旋、涡流消旋等，表1中列出了当前典型消旋方法的基本技术状况。

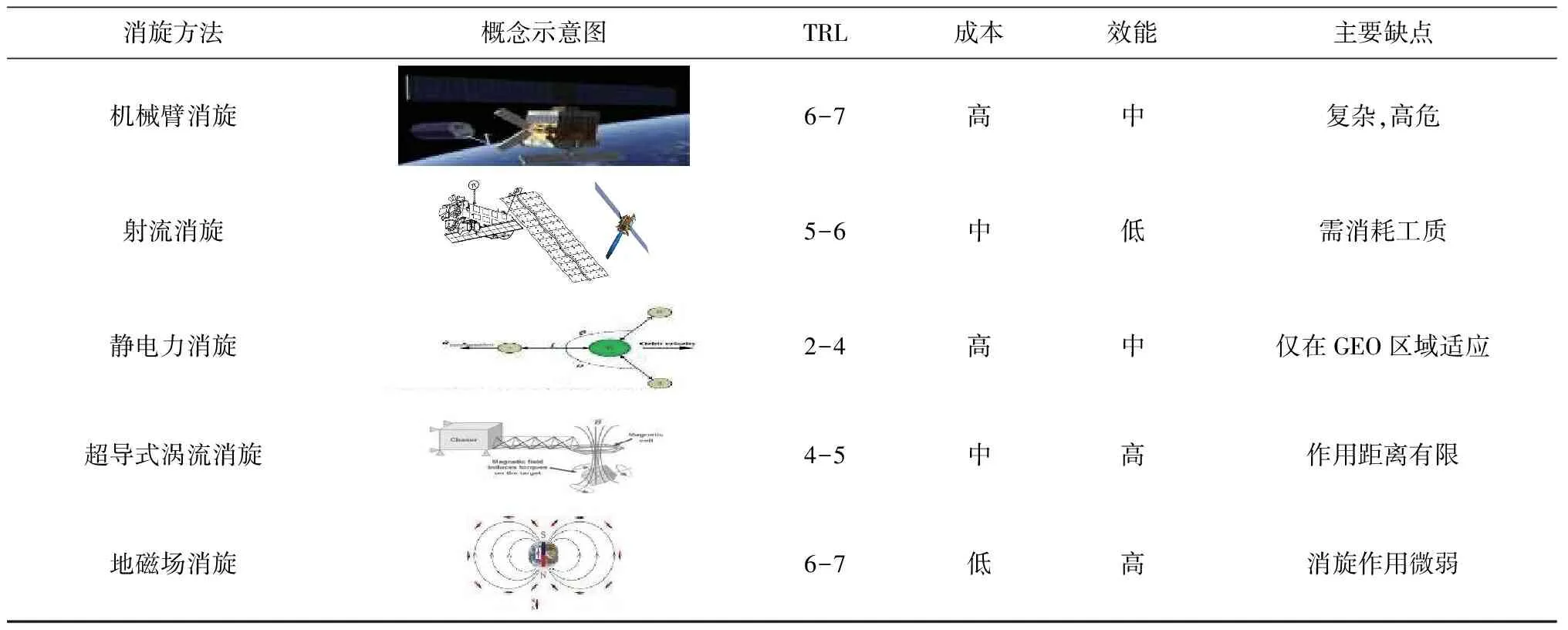
表1 常见消旋方法的比较Table 1 Tradeoff analysis of typical despin approaches

机械臂消旋的方法最早受到重视，目前其技术成熟度(TRL)最高，然而，实际工程应用中，对翻滚非合作目标进行操作是非常复杂的，极易发生碰撞[15]。射流消旋是服务星使用自身的某个推力器对准目标星喷射尾流工质，形成相对于目标质心的力矩从而消除旋转。由于射流消旋需要持续喷射工质，且喷射的准确性很难掌控，导致该方法难以实践[14]。静电力消旋是利用电子束枪向目标星喷射电荷使其带电，形成相互排斥或吸引的静电力以进行制动，考虑到空间等离子体对静电力的屏蔽，该方法仅适合高轨目标的消旋[13]。与涡流消旋类似，地磁场消旋是利用地球磁场下的涡流力矩进行消旋，但由于自然条件下的地磁场很小，其涡流力矩十分微弱[16]。

通过对以上五种消旋方式的权衡比较可知，超导式涡流消旋具有非接触、无需燃料、适应于高转速、便于操作等优势，超导式涡流消旋是极具发展潜力的一种消旋方式。尽管涡流消旋的技术成熟度还比较低(4～5级)，然而一旦相关技术得到突破，涡流消旋将具有极大的实用性和适用性。

2.2 超导式涡流消旋的技术可行性

1)涡流消旋的物理原理真实可靠

涡流消旋的物理原理可以用电磁阻尼、楞次定律来解释，这些物理学上的原理或现象早在100多年前就已经被发现并得到证实。

2)地面涡流制动技术业已成熟

涡流制动在工业生产中的应用已经十分广泛，如列车涡流制动器，这为空间环境下涡流制动提供了参照对象和经验。从某种程度上来说，只需要把地面涡流制动技术“转移”到太空环境[12]即可。

3)航天器涡流消旋具有充足的客观条件

涡流消旋的目标星并不需要安装专门的消旋装置，仅要求目标星上有导电结构。幸运的是，目前大部分航天器都是采用高电导率的金属材料制造的，这为涡流消旋提供了“天然具足”的作业条件。另外，超导电磁线圈可很轻松地为目标提供大于10-4特斯拉的磁场，地球磁场的影响可以忽略不计。

4)高温超导技术的进步

第二代高温超导材料的临界温度(约为77 K)大于太空的平均温度(约4 K)，这使得高温超导材料非常适合用于太空。另外，超导线圈的导电能力是常导线圈的百余倍，超导式消旋的制动能更强。

以上权衡分析、技术评估定性地说明了涡流消旋技术是可行的优选方法，接下来的第3节、第4节，将建立涡流消旋问题的精确模型并对典型消旋案例进行仿真，进而定量地研究涡流消旋的能力水平及其制动特性。

3 超导式涡流消旋的模型

3.1 涡流消旋的精确建模

涡流消旋过程依次对应磁场模型、电场模型、涡流力矩模型、编队动力学模型[17]。与传统的飞行动力学不同，航天器涡流消旋包含电场、磁场和涡流力矩等特有的模型，其中，磁场模型和涡流力矩模型是分析涡流消旋作用大小、设计电磁消旋装置的根本，本小节分别建立这两者的数学模型。

3.1.1超导线圈的磁场模型

磁感应强度用符号B表示，它表示垂直于磁力线方向的单位面积上所通过的磁力线数目。由于磁感应强度的散度处处等于零，因此，磁感应强度B可以写成矢量磁位A的旋度的形式。

(1)

令超导电磁线圈的匝数为N，线圈半径为R，导线中的电流为i。当各砸线圈紧密排列，且线圈绕组的粗细程度远小于线圈半径时，电磁线圈可以看作一个大的载流环(如图3所示)，则空间某点s处的矢量磁位A可以表示为电流微元dl沿载流环路的积分。

(2)

将式(2)代入式(1)得

(3)

(4)

式(3)可以简化为：

(5)

式(5)是电磁线圈磁场的精确计算公式，然而沿电流线圈的曲线积分很难显示地表达出来，磁感应强度仅能写成如下带椭圆积分的解析式

B(s)=Bx·x+Br·r=

(6)

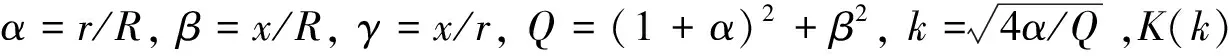
图3 电磁线圈磁场及消旋目标动力学分析Fig.3 Magnetic field of superconducting coil and kinetic analysis of despin target

3.1.2涡流力矩模型

涡流力矩模型是实施涡流消旋的前提，然而，由于目标卫星特殊的几何外形、金属材料各向异性使得涡流力矩很难计算。对于不规则的目标，一般采取有限元方法；而对于球形、圆柱形、盘形等规则目标，文献[18]给出了涡流力矩的解析计算式。本文使用文献[5]中所提出的电磁张量理论，根据激励磁场强度直接求出涡流力矩。首先，在均匀恒定的磁场中，球形目标卫星的涡流力矩模型为：

Tct=(M(ω×BGt))×BGt

(7)

(8)

它与轴线外任意点的磁感应强度B(s)是不相同的。非均匀磁场下涡流力矩与均匀磁场下涡流力矩存在一定误差。精确的涡流力矩计算公式可通过式(7)乘以一个非均匀磁场有效因子μeff来修正，根据文献[11]，有效因子μeff的计算公式可展开为：

(9)

式中:θ是球体内的方位角，Bo是目标体内点O=[d,Rtcosθ, 0]T处的磁场强度，点O及角θ如图3所示。

经过修正后的非均匀磁场下球形目标的有效电磁张量为：

(10)

最后得电磁线圈磁场下涡流力矩的精确计算式为：

(ω×BGt)×BGt

(11)

3.2 涡流消旋的仿真模型

在涡流力矩作用下，目标星转速的衰减是一个复杂非线性变化过程，本节根据某典型失效卫星及实际消旋任务需求，给出航天器涡流消旋的动力学仿真模型，以便研究涡流消旋的具体过程。

1)超导电磁线圈模型

采用第3.1节中的电磁场计算公式，具体参数设置为：线圈半径2 m，线圈绕组匝数800匝，通电电流100 A。

2)目标星模型

以我国某经典卫星作为消旋目标，该卫星是一个72面体，仿真模型中可将其近似为球体，球壳材料为硬铝合金，表2给出该失效目标星的物理参数。

表2 消旋目标星的物理参数Table 2 Physical parametersof the despin target object

3)目标星姿态运动模型

本文重点关注目标星在涡流力矩作用下的消旋过程，可假设消旋过程中服务星通过自身的姿轨控制，保持与目标星之间的距离和指向恒定不变，电磁线圈的中心轴线过目标星重心，目标星的自旋轴垂直于线圈的中心轴线，线圈中心点到目标引力中心COG的距离d(见图3)为10 m；根据式(9)，计算得10 m处磁场有效因子μeff=0.994547。

涡流力矩作用下目标星的姿态动力学方程为：

(12)

式中:ω是目标星固连系相对于电磁线圈的角速度。

4 消旋案例仿真研究

结合典型消旋任务，利用上述数学模型和仿真模型，本节对超导电磁线圈及其制动能力进行综合分析，通过多组案例的仿真计算来定量地研究并验证涡流消旋的有效性和实用性。

4.1 高/低速自旋目标的消旋

空间观测显示，有些失效目标的转速仅为1(°)/s，有的[5- 9]高达180(°)/s，本处设定目标的初始转速依次为：[50, 150, 250, 350, 450, 550](°)/s，这样一组不同转速目标的仿真试验是为了检验同一电磁线圈对高速和低速旋转目标的消旋效果。各目标的消旋仿真均采用第3.2节中的模型。仿真得到的目标卫星自旋角速度和涡流力矩变化曲线如图4、图5所示。

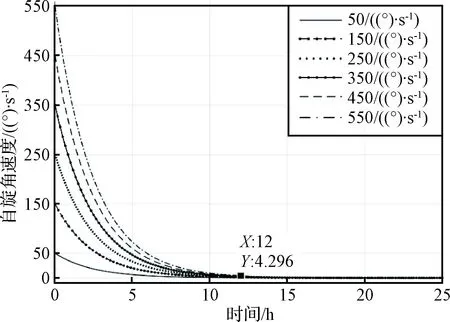
图4 目标卫星自旋角速度随时间的变化曲线Fig.4 Curves of rotational speed vs. time of despin targets

图5 目标卫星所受到的涡流力矩随时间变化的曲线Fig.5 Curves of brake torque vs. time of despin targets

从图4可以看出，在磁场的持续作用下，各目标自旋速度均明显减小，24 h之内，均降到了10(°)/s以下。初始转速为550(°)/s的目标持续消旋半天，转速迅速下降到4.296(°)/s，而初始转速为50(°)/s的目标，5 h后转速才降到6.621(°)/s，这说明消旋的快慢与目标转速密切相关。

图5所示涡流力矩变化曲线中，制动力矩随目标角速度的下降而减小，在起始时刻，涡流力矩约为10-2N·m，10 h后涡流力矩迅速下降到10-4N·m。即目标转速越小，涡流力矩随之变小，此时，制动作用越微弱，越难消除目标的微小自旋。

总的来看，高速、低速旋转目标均可被涡流力矩有效消旋，当目标初始转速从50(°)/s上升到550(°)/s(上升11倍)，涡流消旋所需时间仅仅从6 h(取消旋的末端速度为4.296(°)/s)增加到12 h，也就是说，目标转速越高，制动的速度也越快，涡流消旋非常适合对高转速目标进行消旋。

4.2 复合旋转目标的消旋

考虑到失效目标的实际旋转运动非常复杂，自旋且附加章动的复合旋转运动十分常见。为了检验涡流消旋对复合旋转的制动能力，本小节对复合旋转目标的消旋进行仿真。目标的初始转速设为ω0=[14.4, 57.6, 0](°)/s，初始时刻章动角约为14°。

目标星自旋轴y方向初始速度ω0y为57.6 (°)/s，消旋10 h后，转速单调地下降到1.693 (°)/s(见图6左侧)；然而，x轴向和z轴向的角速度分量分别为余弦波式和正弦波式衰减(见图6右侧)。经过10 h的消旋，章动角速度从14.40(°)/s减小到1.9021(°)/s。由此可知，自旋和章动同时得到了消除，涡流消旋具有同时消除多个方向转动角速度的能力。

观察涡流力矩曲线图7，自旋轴向的力矩从初始的53.18 mN·m快速且单调地下降，在10 h处，制动力矩减小到0.1563 mN·m。z轴向制动力矩是余弦波式逐渐衰减的。由于线圈坐标系的x轴始终与磁感应强度方向平行，x轴向的涡流力矩恒为零，这与自旋目标的消旋截然不同。从而可得结论：自旋角速度和章动角速度被同时消除，但章动角速度的消减是简谐式的，而自旋角速度是单调递减的。

为了更直观展示复合旋转的消旋过程，图8绘制了目标星动量矩的三维曲线图，图中黑色圆圈表示初始时刻的动量矩为55.5624(kg·m2·s-1)。随着消旋的推进，动量矩沿负y轴向螺旋式地消减，25 h后动量矩减小到0.0924(kg·m2·s-1)。为了更清楚地观察，将最后2.5 h内(第22.5 h到25 h)的动量矩曲线放大，从图8右侧的局部放大图可清晰地观察到动量矩矢量衰减所形成的三维螺旋曲线。很明显，该曲线有收敛到零点[0, 0, 0]的趋势。

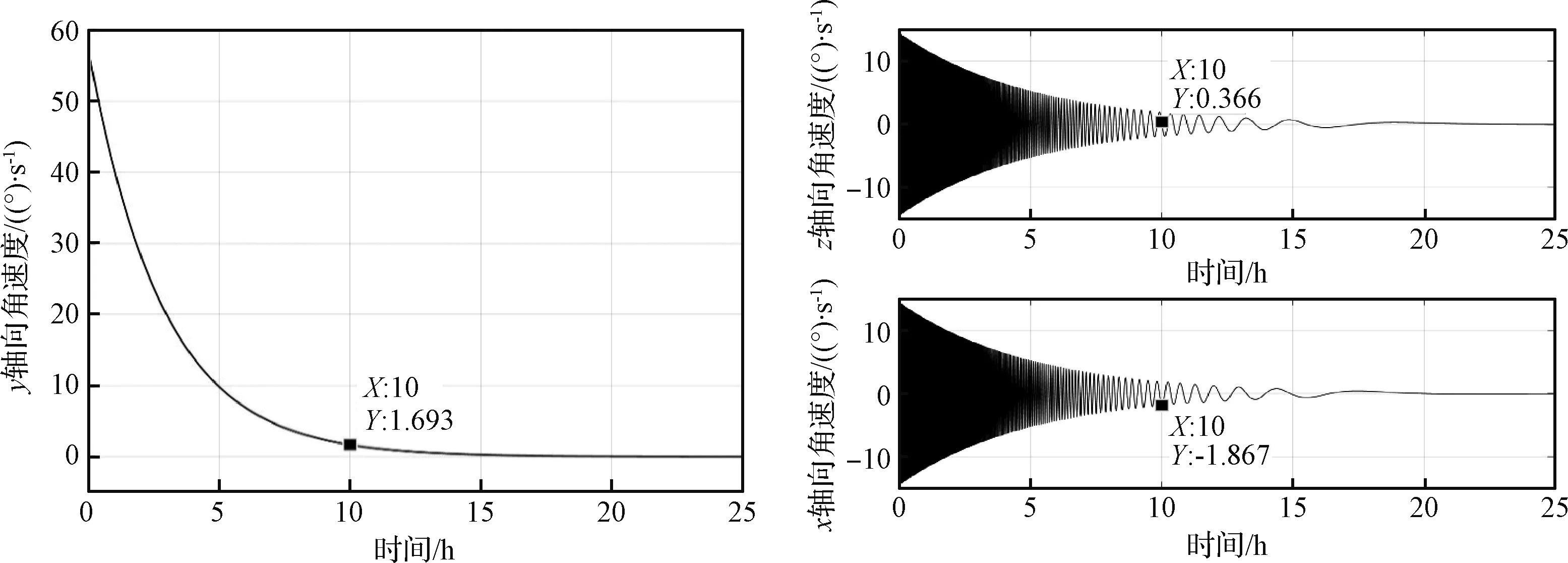
图6 目标卫星角速度随时间的变化曲线Fig.6 Curves of rotational speed vs. time of the tumbling target

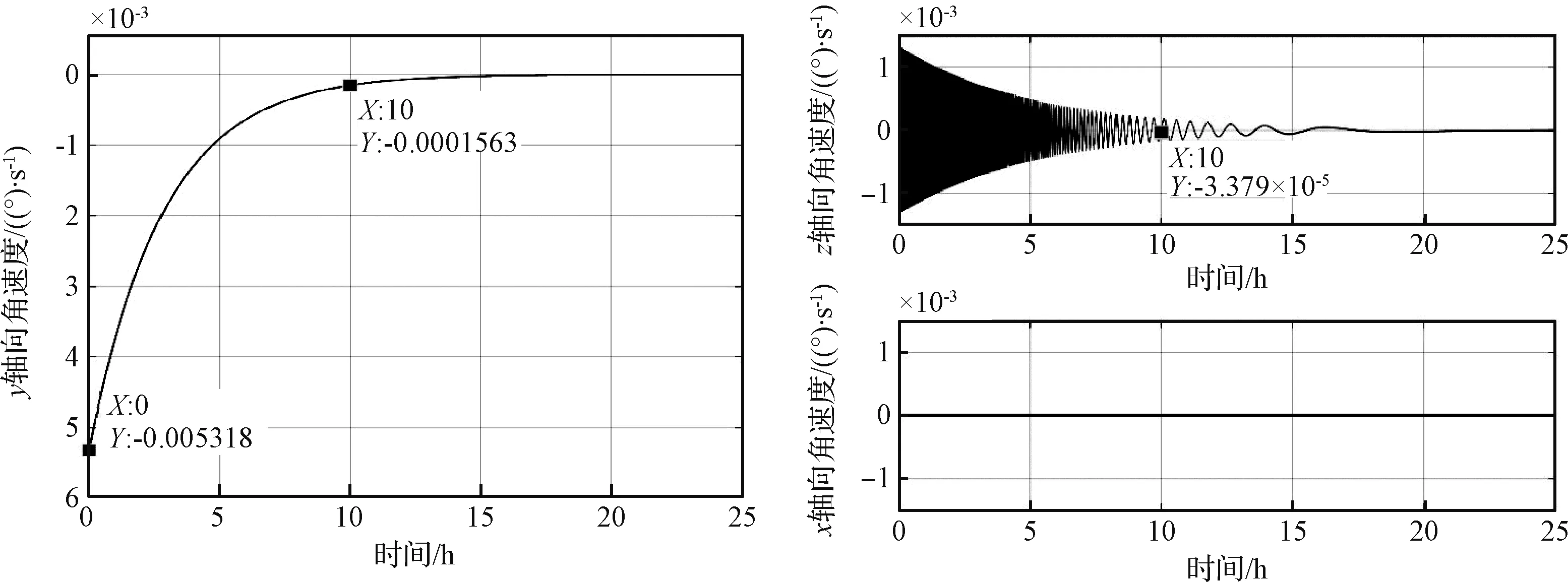
图7 目标卫星所受到涡流力矩随时间变化的曲线Fig.7 Curves of brake torque vs. time of the tumbling target

图8 目标卫星动量矩随时间变化的曲线Fig.8 3D-curve of target’s angular momentum

4.3 定量分析结果

由上述仿真分析可知，涡流消旋具有足够的制动能力，能将复合旋转空间目标完全消旋，超导式涡流消旋具备在几十个小时内将高速旋转目标消减到几度每秒的制动水平。

归纳得出超导式涡流消旋的研究结果为：超导式涡流消旋有适宜的太空环境及导电的消旋目标，涡流消旋具有足够的制动能力和水平，相关技术已获得长足进步。总而言之，超导式涡流消旋的概念是可信的，涡流消旋的制动能力足以执行航天消旋任务，其工程应用具有充足的技术可行性。

5 结 论

本文针对空间旋转目标的消旋问题，提出超导式涡流消旋的原型概念，分析了涡流消旋的机理，建立了超导电磁线圈精确的磁场模型、涡流力矩模型。利用超导电磁线圈对典型目标进行了仿真试验，得到的主要结论有：1)涡流消旋具有快速制动高转速目标、复合旋转目标的能力；2)消旋操作时，应将线圈中心轴线垂直地对准目标角速度分量最大的方向，以获得最大的消旋作用效果。与同类研究相比，本文提出了独具特色的连杆机构形式的原型概念，将消旋能力提高到550 (°)/s，并首次对高/低速、复合旋转目标进行综合仿真分析。本文通过对涡流消旋定性和定量的分析研究，总体上论证了超导式涡流消旋的技术水平和制动能力，所得到的研究结果可直接用于下一步的工程设计中。