钢轨廓形偏差对动车组构架横向振动的影响
杨光 侯茂锐 刘丰收 俞喆
1.中国铁道科学研究院集团有限公司金属及化学研究所,北京 100081;2.中国铁道科学研究院集团有限公司铁道科学技术研究发展中心,北京 100081
高速动车组服役性能与轮轨型面匹配状态密切关联[1-2]。钢轨廓形作为轮轨型面匹配关系中的关键要素之一,其偏差状态直接影响轮轨匹配状态,进而影响动车组运行品质。文献[3]研究表明,磨耗轮与轨距角突出的钢轨匹配时等效锥度较大,易产生横向加速度超限;新车轮与轨距角被过度打磨的钢轨匹配时等效锥度较小,易产生晃车。文献[4-5]分别研究了钢轨打磨对动车组车体抖动和车体晃动的影响。文献[6]指出动车组抖车是由于车轮与钢轨匹配关系异常,导致转向架蛇行运动频率达到9 ~ 10 Hz,与动车组车体一阶菱形模态频率接近,引发车体产生异常振动。文献[7-8]通过运营动车组跟踪测试,明确了动车组车体出现晃动时的主频为1~2 Hz。
目前关于钢轨廓形偏差量细微变化对动车组运行性能影响的相关研究较少,也尚未明确不同钢轨偏差量与动车组运行性能的量化关联关系。由于抖车、晃车现象均与转向架蛇行运动稳定性相关,本文基于高速铁路实测轮轨型面数据,仿真分析不同偏差的钢轨廓形分别与新车轮、磨耗车轮匹配时的轮轨匹配状态,以及钢轨廓形偏差引起轮轨匹配状态变化对动车组构架横向振动的影响。
1 钢轨廓形偏差
通过轮轨型面长期跟踪测试得到的我国京沪、京广等高速铁路钢轨廓形数据[9],以Q/CR 681—2018《高速铁路钢轨与道岔大型机械打磨验收技术规范》规定的设计廓形为基准廓形。计算工作边侧距离轨顶中心20 mm 位置实测钢轨廓形与基准廓形的偏差d,选取d= -0.4、-0.2、+0.3、+0.6、+0.8 mm 的典型廓形(依次用d-0.4、d-0.2、d+0.3、d+0.6、d+0.8表示)进行动车组动力学性能分析。
将d-0.4、d+0.8廓形分别与基准廓形进行对比,结果见图1。可知:①两种实测廓形与基准廓形在距轨顶中心-35 ~ -10 mm 区域(非工作边侧)和10 ~ 35 mm区域(工作边侧)均存在明显的差异。d-0.4廓形在距轨顶中心10~35 mm 区域明显低于基准廓形,即与基准廓形存在负偏差;d+0.8廓形在距轨顶中心10 ~ 35 mm区域明显高于基准廓形,即与基准廓形存在正偏差。②在工作边侧,随着与轨顶中心横向距离增大,两种实测廓形与基准廓形的偏差均呈增大趋势。其中,d+0.8廓形在与轨顶中心的距离超过25 mm 后,偏差大于1 mm。

图1 钢轨廓形及偏差分析
等效锥度是反映轮轨型面匹配状态的关键指标之一。既有研究及现场运用经验表明[3],钢轨廓形偏差影响其与车轮匹配时的等效锥度,进而影响动车组运行品质。等效锥度较低可能出现晃车,等效锥度过大可能出现抖车或报警,均影响动车组运行时的横向平稳性。
图2给出了不同偏差实测钢轨廓形与某型动车组新车轮和临近镟修的磨耗车轮匹配时的名义等效锥度。可知:①对于新轮和磨耗车轮,钢轨廓形偏差对等效锥度均有显著影响。负偏差越大则等效锥度越小,负偏差大于0.2 mm 时名义等效锥度小于0.08;正偏差越大则名义等效锥度越大,正偏差达到0.6 mm时名义等效锥度超过0.45。②不同偏差实测钢轨廓形与磨耗车轮匹配对应的名义等效锥度均明显大于新车轮踏面,两种车轮踏面对应名义等效锥度的差异随负偏差减小而增大,随正偏差增大而增大。
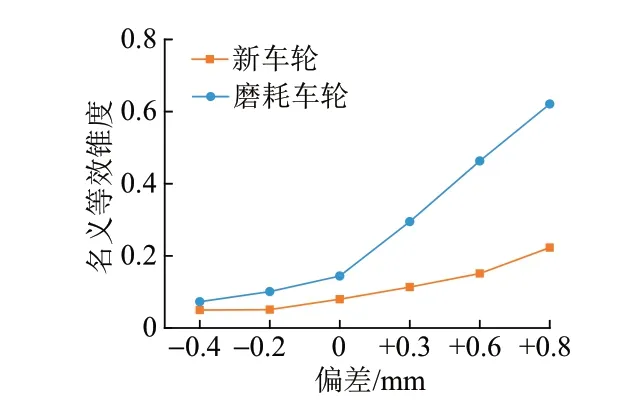
图2 轮轨匹配等效锥度
新车轮分别与d-0.4、d+0.8廓形匹配时,左股轮轨接触分布及现场光带情况见图3。可知:d-0.4廓形对应的轮轨接触点相对集中,且偏向非工作边,这与图3(b)中现场光带情况一致,光带中心偏非工作边,宽度约为25 mm;d+0.8廓形对应的轮轨接触点分布相对分散,在轨顶中心至轨距角区域均有分布,与图3(c)中现场光带情况接近,光带中心偏工作边,宽度约为40 mm。

图3 轮轨接触范围及钢轨光带
2 构架横向振动加速度
构架横向振动加速度是评判车辆运行稳定性的关键指标之一。基于实际动车组和线路参数建立轮轨系统耦合动力学模型,仿真分析不同偏差钢轨廓形与新车轮、磨耗车轮匹配状态下的构架横向振动加速度,计算结果见图4。可知:不同偏差的钢轨廓形与磨耗车轮匹配时横向变化更明显,车轮磨耗后,随着d由-0.4 mm 增至+0.8 mm,构架横向振动加速度呈现明显增大趋势,尤其是钢轨存在较大正偏差后,d+0.8廓形对应的构架横向振动加速度较d+0.6廓形增大近80%,较基准廓形增大近2 倍;与新车轮匹配时,负偏差钢轨廓形对应的构架横向振动加速度相对较大,但与基准廓形的差异不超过20%。
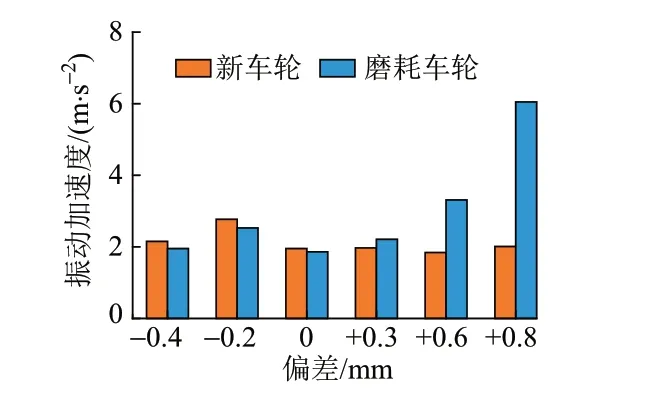
图4 不同偏差钢轨廓形的构架横向振动加速度
为了分析钢轨正偏差增大后构架横向振动加速度明显增大的原因,截取d+0.8廓形和基准廓形与磨耗车轮匹配时的仿真计算结果(图5),对比分析构架横向振动加速度时频特征差异。
由图5(a)可知:与磨耗车轮匹配时,d+0.8廓形对应的构架横向振动加速度最大值达5.80 m/s2,有效值为2.76 m/s2,而基准廓形对应值分别为1.90、0.65 m/s2。可见d+0.8廓形对应的构架横向振动加速度振动幅度和振动剧烈程度均明显大于基准廓形。同时,d+0.8廓形对应的构架横向振动加速度时域变化已表现出明显的周期性振荡特征,这说明该匹配关系下构架已出现蛇行失稳。

图5 与磨耗车轮匹配时构架横向振动加速度时频曲线
由图5(b)可知:基准廓形对应的构架横向振动加速度主频特征不明显,在2~3 Hz振动幅值相对较大;d+0.8廓形对应的构架横向振动加速度出现了明显8 ~10 Hz 的频域特征,这与运营动车组发生抖车时的构架横向振动加速度频率特征[6]十分接近,且该频域范围构架横向振动幅值明显大于基准廓形。
综上,较大正偏差的钢轨廓形与磨耗车轮匹配时,构架已出现明显二次蛇行失稳现象,构架横向振动幅值和振动剧烈程度相对基准廓形均明显增大。
根据现场应用情况,不同运行速度的车辆运行性能对于轮轨匹配状态的敏感性也存在差异。因此,需进一步分析不同车速下,不同偏差钢轨廓形与新车轮、磨耗车轮匹配时的构架横向振动加速度情况。车速分别为300、350、400 km/h 时,各轮轨匹配工况下构架横向振动加速度最大值仿真计算结果见图6。
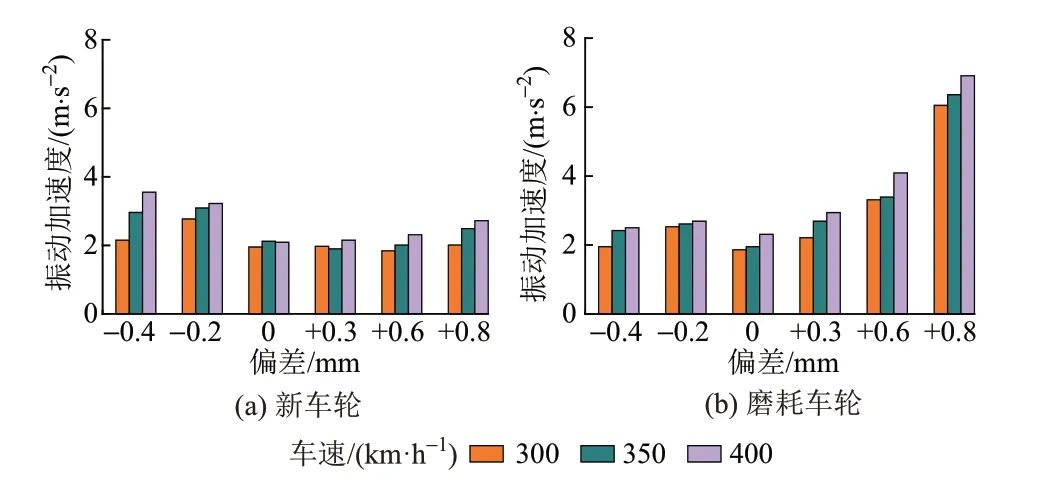
图6 不同车速下构架横向振动加速度
由图6可知:①不同轮轨匹配工况下,构架横向振动加速度随车速提升而增大。②新车轮与负偏差钢轨廓形匹配对应的构架横向振动加速度受车速影响更为明显,如d-0.4廓形与新车轮匹配工况下,车速350、400 km/h时构架横向振动加速度分别比车速300 km/h时增大38%、65%。d+0.8廓形与磨耗车轮匹配工况下,车速400 km/h时构架横向振动加速度比车速350 km/h时仅增大10%,这是由于较大正偏差车轮与磨耗车轮匹配工况下,以350 km/h 运行时已处于构架蛇行失稳状态,车速对于构架横向振动加速度的影响作用不及正常运行状态下明显。
选择构架横向振动加速度变化更为明显的d-0.4廓形与新车轮匹配工况,分析不同速度条件下构架横向振动加速度的时频特征。仿真计算结果见图7。

图7 d-0.4廓形与新车轮匹配时构架横向振动加速度
由图7 可知:①d-0.4廓形与新车轮匹配工况下,随着速度提高,构架横向振动更加剧烈。车速300、350、400 km/h 对应的构架横向振动加速度有效值分别为0.62、0.69、0.77 m/s2,车速400 km/h 对应的构架横向振动加速度有效值比车速300 km/h 增加24%。②三种速度对应的构架横向振动加速度主频均为1.5 Hz,该频率特征与现场出现低锥度晃车时的频率特征[7]十分接近,且随速度提高,1.5 Hz 频率对应的振动幅值明显增大。可见,较大负偏差钢轨廓形与新车轮匹配时,速度提高将增大构架横向振动加速度低频振动幅值,加剧构架横向振动,增加车辆低频失稳风险。
3 结论
1)不同偏差实测钢轨廓形与磨耗车轮匹配对应的名义等效锥度均明显大于新车轮,名义等效锥度随负偏差减小而增大,随正偏差增大而增大。
2)不同偏差钢轨廓形对应轮轨接触点分布与现场钢轨光带分布特征对应。负偏差钢轨廓形对应轮轨接触范围相对集中,正偏差钢轨廓形对应的轮轨接触范围相对分散。
3)不同偏差钢轨廓形与磨耗车轮匹配时的横向振动加速度变化更明显,钢轨廓形偏差由-0.4 mm到+0.8 mm,构架横向振动加速度呈现明显增大趋势。较大正偏差钢轨廓形与磨耗车轮匹配时,构架横向振动幅值和振动剧烈程度相对基准廓形均会明显增大,偏差+0.8 mm廓形对应的构架横向振动加速度幅值较基准廓形增大近2 倍,已出现了明显的构架蛇行失稳现象,且存在8~10 Hz的抖车频率特征。
4)不同轮轨型面匹配组合下,构架横向振动加速度幅值均随速度提高而增大。较大负偏差钢轨廓形与新车轮匹配时,速度提高将增大构架1.5 Hz 低频振动幅值,加剧构架横向振动,增加车辆低频失稳风险。

