高速列车车轮踏面剥离引起的轮轨冲击力学响应有限元模拟*

王金能，郭 鑫,2，敬 霖，王开云

（1. 西南交通大学牵引动力国家重点实验室，四川 成都 610031；2. 中车戚墅堰机车车辆工艺研究所有限公司，江苏 常州 213011）

随着我国列车高速化、重载化发展，列车服役环境和轮轨间的相互作用关系变得更加复杂，轮轨的磨耗和损伤问题日益突出，轮轨间常常伴随着较大的冲击和振动，加剧了车辆和轨道结构部件的损伤、疲劳和断裂破坏，严重影响列车的运行平稳性和安全性。车轮踏面剥离是轨道车辆车轮非圆化损伤的常见形式之一，通常指车轮在服役过程中受到热机械作用或轮轨滚动接触疲劳，在车轮踏面局部或圆周范围内呈现出的龟纹状或鱼鳞状热裂纹和金属剥落损伤现象，如图1 所示。严格意义上，根据车轮踏面剥离的材料失效机理，由轮轨滚动接触疲劳导致的踏面损伤称为剥落（shelling），而由热机械作用导致的踏面损伤称为剥离（spalling）。但是，由于轮轨间相互作用受外界诸多复杂因素的耦合影响，很难对车轮上出现的踏面剥落或剥离进行准确的区分，因此通常将这类车轮踏面损伤统称为“剥离”。

图1 车轮踏面剥离现场图片（左图[6]，右图[7]）Fig. 1 Pictures of wheel tread spalling (left picture[6], right picture[7])

近年来，对车轮踏面剥离的形成机理及影响因素已有大量研究。在形成机理方面，Cummings 等认为踏面剥离形成的直观原因是轮轨间瞬时高温引起的车轮局部金相组织转变。陶贵闯等开展了不同转数下D2 车轮的滑动磨损试验，发现试样磨损表面会形成纳米晶白层，随着白层不断累积，表面开始萌生裂纹，最终出现金属薄片剥落现象。Zeng 等通过滚动接触疲劳试验和弹塑性有限元法模拟了白层的脱落过程，比较了固溶强化钢和传统钢的层裂行为，发现固溶强化钢可以抑制车轮剥离的发生。在影响因素方面，Wang 等、郭俊等分析了不同滚滑状态下车轮钢的剥离摩擦磨损特性，发现车轮的磨损和剥落行为很大程度上取决于轮轨间的制动力、法向载荷和蠕滑率。Kato 等通过热双盘式滚动接触疲劳试验和弹塑性有限元分析，得到车轮踏面裂纹尖端张开位移随着温度升高、材料屈服应力降低和滚动接触循环次数增加而增大，从而加速疲劳裂纹扩展，导致踏面剥离。Cummings 等通过踏面调节制动装置和高摩擦复合装置对车轮踏面产生剥离的影响试验，发现制动系统从踏面制动改为盘形制动后会加剧踏面剥离现象。此外，一些学者还发现轮对纵向振动不但会使轮轨接触面产生更高的温度和接触应力，而且会改变主应力的方向，容易诱发车轮踏面滚动接触疲劳剥离或局部擦伤剥离。然而，关于车轮踏面剥离引起的轮轨冲击力学响应方面的研究还很匮乏。Кpachob 等开展了含车轮踏面剥离罐车的空/重车走行试验，分析了剥离几何尺寸及列车速度对转向架侧架和摇枕最大应力的影响，发现当车轮踏面剥离深度大于3 mm 时，侧架导框内会产生超出侧架耐久极限的应力。汪金余建立了含有不同尺寸踏面剥离损伤的三维轮轨接触有限元模型，研究了踏面剥离的面积（4～12 mm）和深度（0.5～2 mm）对踏面应力分布的影响。目前，车轮踏面剥离损伤还不能得到完全抑制和有效控制，研究车轮踏面剥离引起的轮轨冲击响应规律与机理可为高速列车轮轨系统服役安全性和可靠性提供技术支持。

本文中采用隐式-显式序列求解方法，基于含车轮踏面剥离的三维轮轨滚动接触有限元模型，研究高速列车车轮踏面剥离引起的轮轨冲击力学响应，分析轮轨冲击过程中的轮轨接触力/压力、接触斑及黏/滑特性、节点速度分布和应力应变状态等响应特征，讨论列车速度、剥离长度和剥离深度等关键参数对轮轨冲击响应的影响。

1 踏面剥离尺寸统计与分析

我国铁路部门对高速列车车轮踏面剥离的容许限度作了严格的规定，但不同车型和不同修程的踏面剥离容许限度也略有差异。《铁路技术管理规程：高速铁路部分》中规定，牵引列车的机车在出段前，车轮踏面上的剥离长度不得超过40 mm，深度不得超过1 mm。《铁路动车组运用维修规则》针对CRH 系列各车型，给出了车轮踏面剥离的镟修限度标准，如表1 所示。文献[21]中针对我国客车车轮踏面上出现的剥离，建议当车轮只有一处剥离时，其长度不得超过30 mm；存在两处剥离时，每处剥离长度不得超过20 mm。可以看出，CRH 系列不同车型对于车轮踏面剥离的镟修限度规定也不尽相同，但总的来说，车轮踏面剥离长度限值介于10～30 mm 之间，剥离深度限值介于0.25～1.5 mm 之间。

表1 CRH 系列各型动车组车轮踏面剥离镟修限度[20]Table 1 Damage tolerances of wheel tread spalling of various types of CRH series EMUs[20]

为了便于研究车轮踏面剥离诱发的轮轨冲击作用机理，根据车轮踏面剥离现场形貌（见图1），可以合理地将其简化为长度、宽度、深度的规则半椭球体。从而可以计算出指定车型踏面剥离的宽度限值，如对于CRH3C 车轮，不同剥离深度对应的剥离宽度限值分别为12.7、9.5 和6.4 mm，剥离宽度与长度的比值介于0.3～0.6 之间。基于上述调研结果，本文中假定剥离宽度与长度的比值为0.4，共选取4 种剥离尺寸（= 20 mm，= 8 mm；= 30 mm，= 12 mm；= 40 mm，= 16 mm；= 50 mm，= 20 mm）和2 种剥离深度（= 1 mm 和= 2 mm）工况开展车轮踏面剥离引起的轮轨动态响应有限元分析。

2 三维轮轨滚动接触有限元模型

2.1 有限元建模

利用Hypermesh 软件建立了如图2 所示的三维轮轨滚动接触有限元模型，包括簧上质量、一系悬挂、轮对和轨道。其中，右侧车轮含有一处规则的半椭球形踏面剥离。模型中将簧上质量简化为质点与一系悬挂相连，一系悬挂采用弹簧-阻尼单元模拟。车轮踏面类型为S1002CN 型，半径= 430 mm；钢轨为CN60 型，长度3 800 mm，轨底坡为1∶40。采用无砟轨道结构，从上到下分别为钢轨、扣件、轨道板、砂浆层、底座和路基。其中，扣件系统在建模过程中采用12 组弹簧-阻尼单元模拟与动态行为密切相关的橡胶垫刚度和阻尼。为保证模型求解精度和计算效率，将踏面剥离与钢轨接触区附近的网格进行了细化，大小为1 mm × 1 mm，其余部位网格进行了合理过渡。整个有限元模型包含4 657 806 个单元和4 974 738 个节点。

图2 三维轮轨滚动接触有限元模型Fig. 2 Three dimention finite element model of wheel-rail rolling contact

车轮和钢轨均采用*MAT_PLASTIC_KINEMATIC 模型来表征材料的弹塑性特性，该模型不但可以模拟材料的随动强化特性，还可以通过 Cowper-Symonds 模型来考虑轮轨材料的应变率效应。轮轨钢的应变率参数分别为= 45 635 s、= 3.21 和=1 733 s、= 0.30。轨下基础结构采用*MAT_ELASTIC 材料模型来描述，而弹簧和阻尼分别选择*MAT_SPRING_ELASTIC 和*MAT_DAMPER_VISCOUS 材料模型来描述。轮轨系统各部件模拟所需的材料力学参数见表2。在路基底部施加固支边界约束，轨道两端施加对称边界约束以实现轨道无限长特性，为保证轮对在滚动过程的自平衡，对车轴端面节点施加了轴向平动约束，并对整个系统施加9.81 m/s的重力加速度。轮/轨、轮/轴间均定义为基于罚函数的自动面-面接触，轨下各部件间均定义为绑定面-面接触，轮轨系统相关参数见表3。

表2 轮轨系统各部件的力学性能参数[25]Table 2 Material parameters of the wheel-rail system components[25]

表3 轮轨系统相关参数[22]Table 3 Parameters related to the wheel-rail system[22]

2.2 隐式-显式序列求解

为了考虑轮轨系统初始应力的影响，采用隐式-显式序列求解方法来研究车轮踏面剥离引起的轮轨冲击力学响应，计算求解实施过程如图3 所示。首先，在初始位置点采用ANASYS 隐式算法求解轮轨系统在重力场作用下的静态位移场（静态隐式解），将其输入到有限元模型中进行“应力初始化”；同时，通过在轮对上施加平动速度和相应的转动角速度ω 以实现轮对在钢轨上的滚动，通过对轮对施加相应的转矩来模拟轮轨切向接触力；然后，采用LS-DYNA 显式算法求解轮轨接触动态响应过程（动态显式解）。为避免初始激扰的影响，设置段（动态松弛区）来消耗其所携带的能量，从而当车轮到达点时可以近似达到稳态运动，进而在段（稳态求解区）进行分析车轮踏面剥离对轮轨滚动接触行为的影响。整个复杂实施过程选择多核并行求解器（64 核）计算，对于轮对以100 km/h 的速度沿轨道滚动30 ms 时长工况，静态隐式求解需耗费134.4 核时，动态显式求解需耗费179.2 核时。

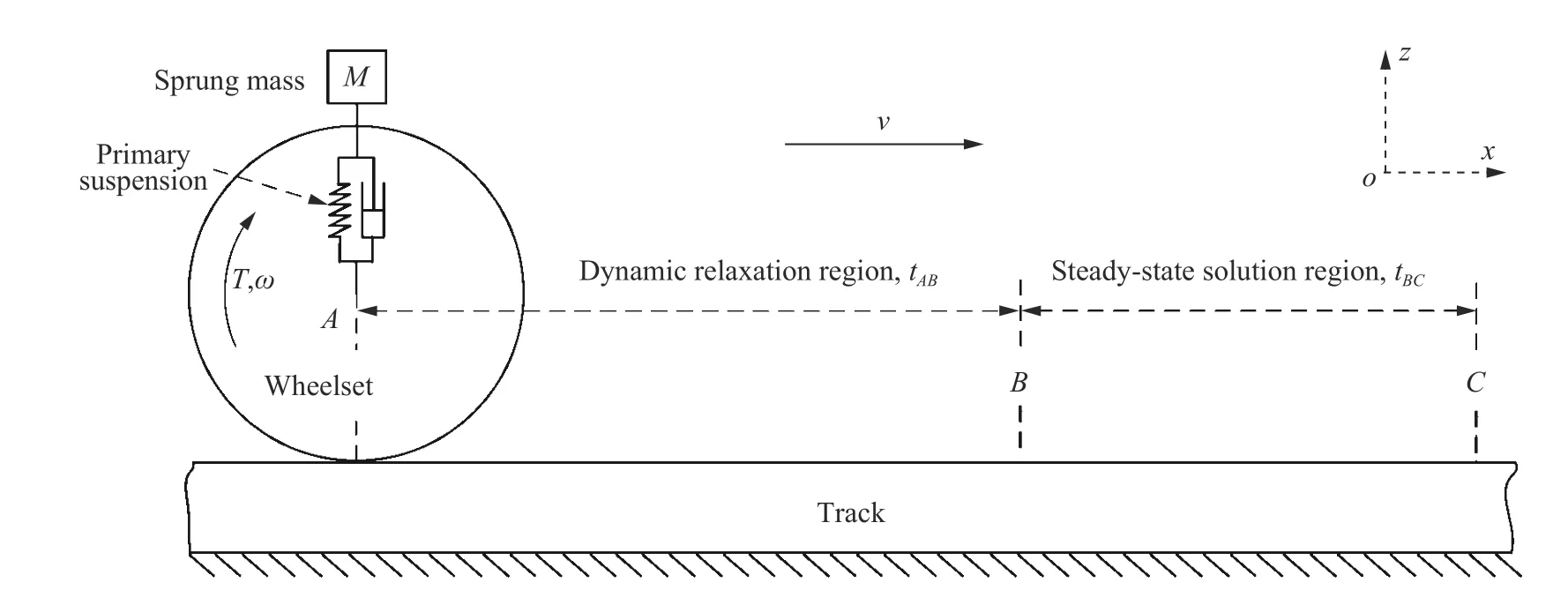
图3 隐式-显式序列求解示意图Fig. 3 Schematic diagram of the implicit-explicit sequence solution method

为确定段的计算时长，采用无缺陷轮对模拟了4 种不同列车速度（100、200、300、400 km/h）下的轮轨滚动接触行为。模拟计算得到的轮轨接触力-时程响应曲线如图4 所示。可以看出，列车速度越高，轮轨动态效应越强，初始激扰的影响越大。列车速度为400 km/h 时，轮轨垂向接触力在20 ms 时的最大波动幅值约为4.6 kN，不超过准静态轮轨垂向接触力（99.3 kN）的4.6 %，而轮轨纵向接触力早已处于稳定状态，表明不同列车速度下轮轨滚动接触行为在20 ms已趋于稳定，有限元结果可用于后续的提取与计算分析。同时，为尽量保证车轮踏面剥离与钢轨接触时已经达到了稳态接触状态，这里设定不同列车速度工况下含踏面剥离车轮与钢轨作用的动态松弛区计算时长t= 22 ms。

图4 不同列车速度下的轮轨接触力时程曲线Fig. 4 Time history curves of the wheel-rail contact forces at different train speeds

3 结果分析与讨论

3.1 轮轨接触力-时程响应

图5 比较了列车速度100 km/h 和踏面剥离尺寸= 40 mm、= 16 mm、= 2 mm 工况下轮对两侧（左侧不含踏面剥离，右侧含踏面剥离）的轮轨接触力-时程响应曲线。可以看出，车轮在滚动至踏面剥离区域之前（＜22.20 ms），轮轨左右侧的垂向、纵向轮轨接触力-时程曲线几乎完全重合，分别稳定在约99.3 和29.8 kN。当轮对滚动至踏面剥离区域（= 22.20 ms）时，出现轮轨接触损失，轮对右侧（含踏面剥离）垂向接触力突然减小，并在= 22.73 ms 时轮轨垂向接触力出现最小值，同时轮轨分别产生向下和向上的速度（见图6），轮轨间产生冲击，且在= 23.76 ms 时出现最大轮轨垂向接触力= 121.5 kN（约为准静态垂向载荷的1.22 倍）。随后，轮对右侧（含踏面剥离）轮轨弹性势能释放，含踏面剥离车轮被弹起，轮轨垂向接触力逐渐减小，直至含踏面剥离车轮回落再次冲击钢轨，引起轮对两侧轮轨垂向接触力的动态振荡并逐渐趋于稳定。轮对两侧的轮轨纵向接触力-时程响应变化趋势和轮轨垂向接触力-时程响应类似，轮对右侧（含踏面剥离）在= 23.76 ms 时出现最大轮轨纵向接触力= 37.5 kN，约为稳态轮轨纵向接触力的1.25 倍。

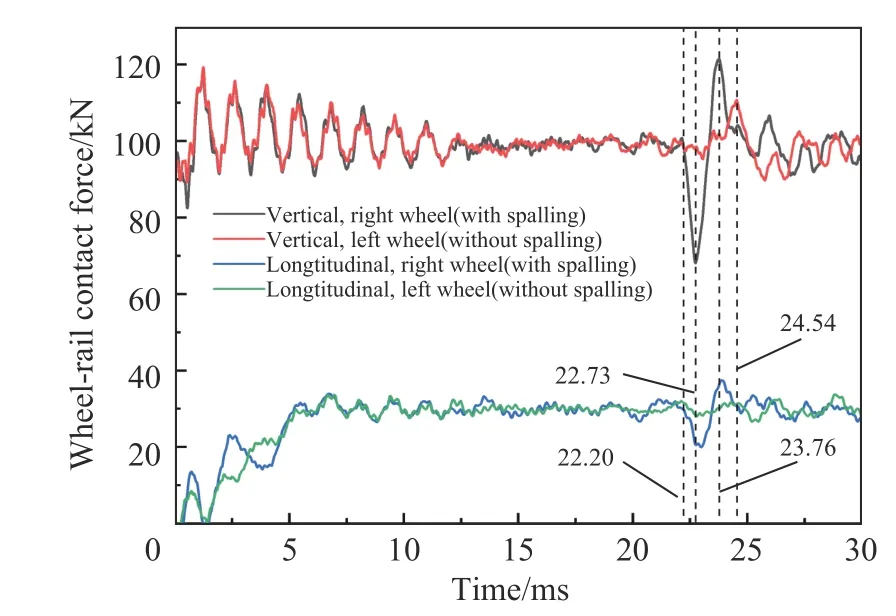
图5 轮轨接触力时程曲线Fig. 5 Time history curves of the wheel-rail contact forces

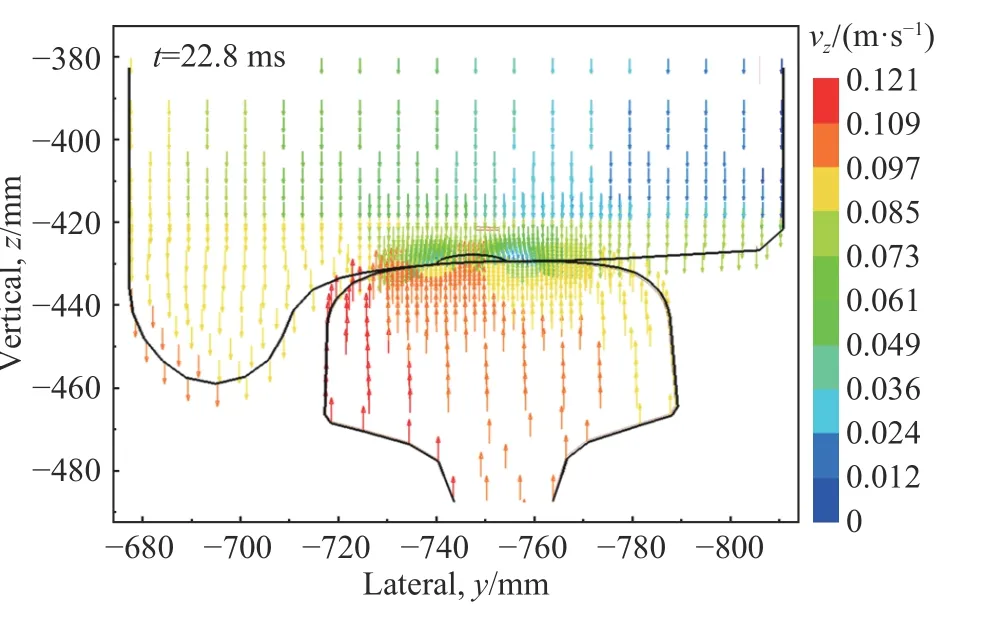
图6 轮轨沿z 向的瞬态速度分布Fig. 6 Wheel-rail velocity distribution along the z direction

3.2 轮轨接触状态

为了深入了解含踏面剥离车轮与钢轨的动态接触过程，图7 中给出了列车速度100 km/h 和踏面剥离尺寸= 40 mm、= 16 mm、= 2 mm 工况下4 个典型时刻的轮轨接触状态（其中红圈为轮轨接触位置）。轮轨接触位置未到达踏面剥离轮廓时（＜ 22.2 ms），轮轨接触状态为单点接触。随着车轮向前滚动，轮轨接触点将沿着踏面剥离轮廓向前滚动，轮轨接触状态由单点接触变为两点接触，且两个接触点分别位于踏面剥离的左右两侧。当轮轨接触位置逐渐远离踏面剥离时，轮轨接触状态向着单点接触逐渐演变，并在= 23.8 ms 时轮轨接触恢复为单点接触。

图7 不同时刻的轮轨接触状态Fig. 7 Wheel-rail contact states at different times

4 个典型时刻对应的轮轨接触斑及黏/滑特性分布如图8 所示。与无踏面缺陷的椭圆形轮轨接触斑不同，含踏面剥离车轮与钢轨的接触斑呈不规则形状，且接触斑内的黏/滑特性分布也存在差异。当=22.2 ms 时，轮轨接触进入踏面剥离区域，黏着区在滚动方向出现了微小缺失；当= 22.7 ms 时，黏着区演变为两部分，滑动区在滚动方向也出现了微小缺失；当= 23.3 ms 时，黏着区和滑动区均变为两部分，分别位于踏面剥离左右两侧；当轮轨接触位置逐渐远离踏面剥离时（= 23.8 ms），左右两侧黏着区和滑动区开始逐渐重合，并向不含踏面缺陷时的轮轨接触状态演变。4 个典型时刻对应的轮轨接触力、接触斑面积和最大接触压力的瞬态响应值见表4。含踏面剥离车轮与钢轨作用过程中，轮轨垂向接触力和接触斑面积均是先减小后增大，而车轮和钢轨的最大接触压力是先增大后减小。这与轮轨接触位置有关，当剥离左右两侧的接触斑沿剥离轮廓远离正常接触位置时，在轮轨垂向接触力相同情况下，会致使接触斑面积减小，而轮/轨接触压力增大。比如，在= 22.2 ms 和= 23.3 ms 两个时刻的轮轨垂向接触力相近，而= 22.2 ms 时刻的接触斑面积约为= 23.3 ms 时刻的1.2 倍，轮/轨最大接触压力远小于= 23.3 ms时刻的。

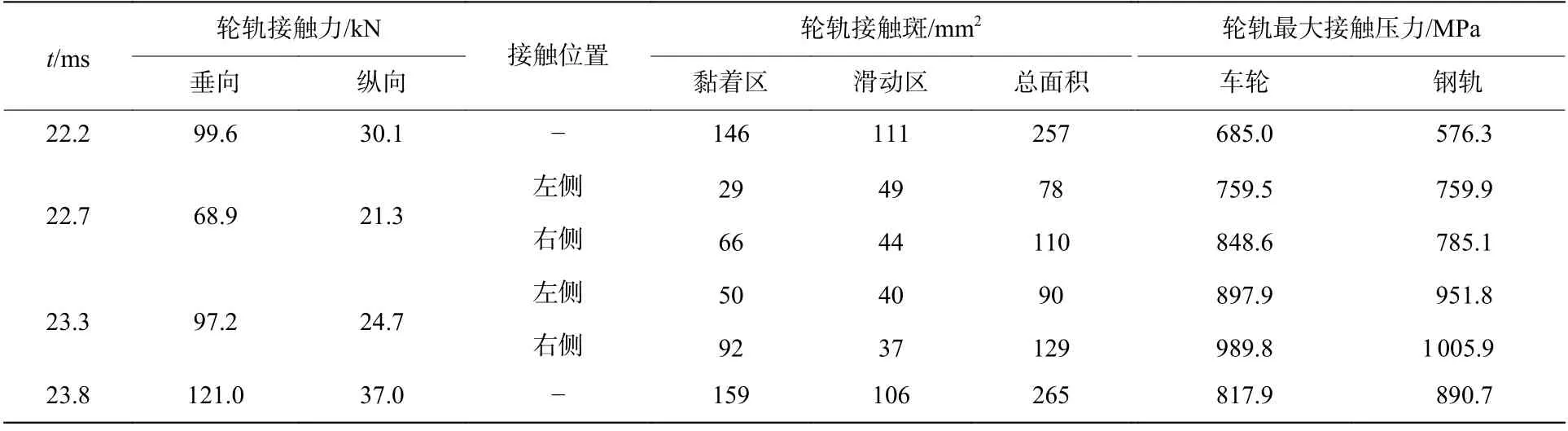
表4 不同时刻的轮轨接触响应Table 4 Wheel-rail contact responses at different times

图8 接触斑内不同时刻的黏/滑状态分布Fig. 8 Distributions of the adhesion-slip areas at different times

3.3 钢轨表面节点速度分布

图9 中给出了列车速度100 km/h、踏面剥离尺寸= 40 mm、= 16 mm、= 2 mm 工况下4 个典型时刻钢轨表面节点沿平面的速度分布。当车轮未进入踏面剥离区域（＜ 22.2 ms）时，接触区后沿（滑动区）节点的速度具有最大值，接触区前沿（黏着区）节点的速度约为零。随着车轮逐渐进入剥离区域（= 22.7 ms），滑动区节点的速度方向分别朝着踏面剥离左右两侧略有偏转，且黏着区和接触区外节点的速度显著提高。随着踏面剥离左右两侧接触区出现分离（= 23.3 ms），两接触区之间节点的速度逐渐减小；由于踏面剥离两侧接触区域承载大小不相等（见表4），导致车轮踏面和钢轨之间会产生几何旋转（自旋），两接触区及其附近节点的速度呈现出了“旋转”的现象。当两接触区重合（= 23.8 ms）时，轮轨冲击力达到最大，轮轨间产生了高频振动和较强的冲击波，会引起轮轨接触区域局部加载和卸载，导致轮轨间产生明显的微滑移，因此钢轨接触区及附近的节点具有较大速度且方向无序。综上所述，在含踏面剥离车轮与钢轨作用过程中，不同时刻钢轨接触区及附近节点沿平面的速度显著提高，且节点速度方向呈无序变化，会加速钢轨表层疲劳损伤。

图9 钢轨表面节点沿xy 平面的速度分布Fig. 9 Velocity distributions of rail surface nodes in the xy plane

3.4 应力和应变状态

图10 为列车速度100 km/h 和踏面剥离尺寸= 40 mm、= 16 mm、= 2 mm 工况下4 个典型时刻的轮轨von Mises 应力分布等值线图。可以发现：车轮踏面剥离与钢轨作用前，车轮von Mises 应力最大值为525.1 MPa，出现在踏面以下约3.5 mm 处，钢轨von Mises 应力最大值为513.7 MPa，出现在接触表层；而车轮踏面剥离与钢轨作用过程中，轮/轨von Mises 应力均显著增大，应力最大值分别为724.6和649.0 MPa，均出现在轮轨接触表层。

图10 不同时刻轮/轨von Mises 应力等值线图Fig. 10 Contours of the von Mises stresses of the wheel-rail at different times

随着车轮逐渐进入踏面剥离区域，踏面剥离宽度的不断增加，导致轮/轨von Mises 应力分布区沿踏面剥离边界开始逐渐分成两部分，且分布范围不断缩小，并在= 22.7 ms 时应力分布范围达到最小，而轮/轨von Mises 应力逐渐增大。随后，轮轨垂向和纵向接触力开始增大，轮/轨von Mises 应力和分布范围随之增大。需要注意的是，当车轮滚动至踏面剥离区域时，出现轮轨接触损失，踏面剥离轮廓边界出现了明显的应力集中，因此= 22.7 ms 时刻踏面剥离左侧车轮von Mises 应力大于= 23.3 ms 时刻的应力值。当车轮逐渐远离踏面剥离区域时，踏面剥离左右两侧应力分布区逐渐重合，轮/轨von Mises 应力开始减小而应力分布范围向四周扩大。此外，通过比较踏面剥离左右两侧的轮轨von Mises 应力分布可以发现，由于踏面剥离左侧承载小于右侧（见表4），左侧轮/轨von Mises 应力分布范围小于剥离右侧；而由于车轮踏面锥度的存在，踏面剥离左侧轮轨局部接触变形大于右侧（见图11），左侧最大轮/轨von Mises 应力大于剥离右侧。

轮/轨等效塑性应变分布云图如图11 所示。车轮较大等效塑性应变分布在距离踏面剥离起点1/4 和3/4 处附近，而钢轨较大等效塑性应变分布在距离踏面剥离起点3/4 处附近，且轮/轨最大等效塑性应变均出现在踏面剥离左侧区域。由于车轮和钢轨材料强度及应变率敏感性的差异，钢轨等效塑性应变最大值（0.010 7）约为车轮等效塑性应变最大值（0.005 4）的2 倍，且钢轨等效塑性应变分布区域明显大于车轮。列车长期运行下踏面剥离处会产生塑性变形和塑性流动，导致剥离两侧边缘区域进一步扩大，将会诱发更强的轮轨冲击；钢轨顶面表层也可能在含踏面剥离车轮多次滚动作用下，随着材料塑性变形的不断累积而产生脱落，并进一步演化为钢轨表面凹坑等缺陷。

图11 轮轨等效塑性应变云图Fig. 11 Contours of the equivalent plastic strain of the wheel-rail

4 参数影响

4.1 列车速度的影响

在踏面剥离尺寸= 40 mm、= 16 mm、= 2 mm 工况下，讨论4 种不同列车速度（100、200、300、400 km/h）对最大轮轨接触力、轮/轨最大von Mises 应力和等效塑性应变等动态响应的影响。图12 为含踏面剥离车轮作用钢轨过程中轮对右侧（含踏面剥离）轮轨接触力的变化曲线。不同列车速度下，轮对到达踏面剥离10 mm 位置处轮轨垂向接触力出现波谷，且随着列车速度的提高轮轨接触损失越明显，并在到达剥离终点附近时出现最大垂向接触力。同时，由于轮轨间微小滑移的存在，致使纵向接触力变化趋势略滞后于垂向接触力。列车速度对轮对左右两侧最大轮轨垂向、纵向接触力的影响如图13 所示。轮对右侧（含踏面剥离）最大垂向接触力随列车速度的提高先增大后减小，在列车速度为300 km/h 时出现最大值133.8 kN，约为准静态垂向载荷的1.35 倍，其随列车速度的变化趋势与车轮扁疤作用钢轨的情形类似。轮对左侧（不含踏面剥离）最大垂向接触力随列车速度的提高而减小，逐渐趋近于准静态垂向载荷。而轮对两侧最大纵向接触力随列车速度的提高分别在36.5 和31.0 kN 附近微小波动。

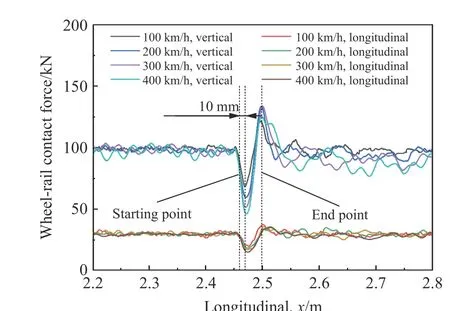
图12 不同列车速度下含剥离侧的轮轨接触力Fig. 12 Wheel-rail contact forces on the spalling side at different train speeds

图13 最大轮轨接触力与列车速度的关系Fig. 13 Relationships between the maximum wheel-rail contact forces and train speed

图14 中给出了轮/轨最大von Mises 应力、最大等效塑性应变与列车速度的关系。通过对比发现，由于轮轨接触几何形状和轮轨材料性能的影响，列车速度对轮/轨的最大von Mises 应力和等效塑性应变的影响规律并不一致。其中，车轮最大von Mises 应力与列车速度呈非单调关系，在列车速度为200 km/h时出现最大值729.1 MPa；车轮最大等效塑性应变随列车速度的提高先增大后减小，同样在200 km/h 时出现最大值0.005 5。而钢轨最大von Mises 应力和等效塑性应变随列车速度的提高先减小后增大，均在100 km/h 时出现最大值，von Mises 应力为684.6 MPa，等效塑性应变为0.010 7。此外，不同列车速度下，车轮的最大von Mises 应力均大于钢轨，而车轮的最大等效塑性应变远小于钢轨。

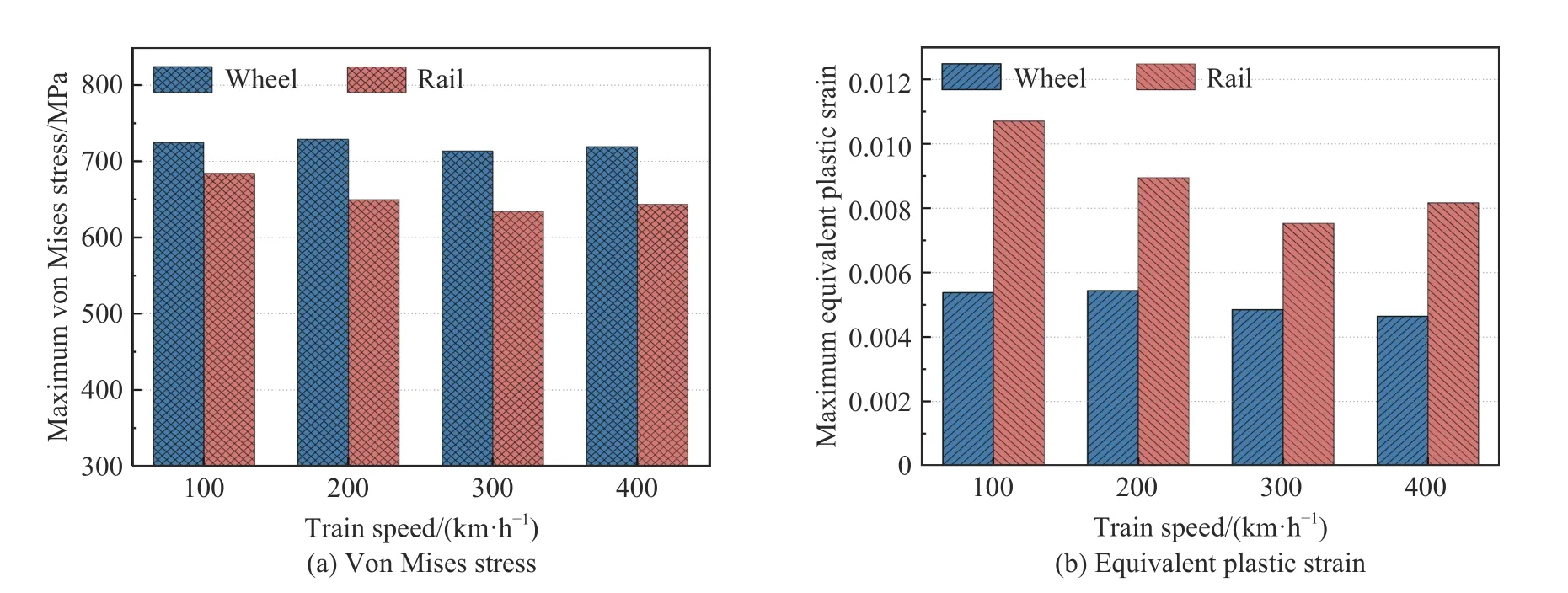
图14 轮轨最大von Mises 应力和最大等效塑性应变与列车速度的关系Fig. 14 Relationships between the maximum von Mises stress and maximum equivalent plastic strain of the wheel-rail vs. the train speed

4.2 剥离长度的影响

列车速度100 km/h 和踏面剥离深度= 2 mm 工况下，讨论4 种剥离长度（= 20，30，40，50 mm）对最大轮轨接触力、轮轨最大von Mises 应力和等效塑性应变等响应的影响。图15 为含踏面剥离车轮作用钢轨过程中轮对右侧（含踏面剥离）轮轨接触力的变化曲线。不同剥离长度工况下，轮对到达剥离起点10 mm 附近处轮轨垂向接触力出现波谷，且随着剥离长度的增大轮轨接触损失越明显，并在剥离终点附近出现轮轨垂向接触力最大值。同样，轮轨纵向接触力变化趋势略滞后于垂向接触力。图16 中给出了剥离长度对轮对两侧最大轮轨垂向和纵向接触力的影响规律。可以看出，轮轨垂向和纵向接触力的最大值均与剥离长度呈单调递增关系。轮对两侧轮轨垂向接触力最大值和纵向接触力最大值与剥离长度均呈一次函数关系（= 1，含踏面剥离侧；= 2，无踏面剥离侧），采用下式进行拟合（拟合系数≈ 0.98）：

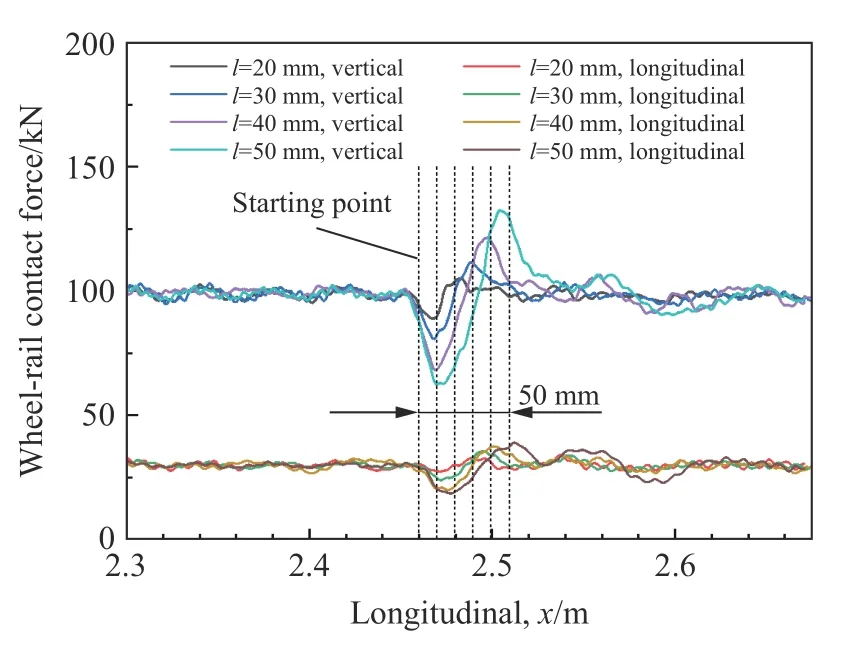
图15 不同剥离长度下含剥离侧轮轨接触力Fig. 15 Wheel-rail contact forces on the spalling side at different spalling lengths

图16 最大轮轨接触力与剥离长度的关系Fig. 16 Relationships between the maximum wheel-rail contact forces vs. the spalling length

式中：拟合参数= 0.919 kN/mm，= 85.56 kN；= 0.505 kN/mm，= 90.9 kN；= 0.201 kN/mm，= 29.24 kN；= 0.027 kN/mm，= 30.68 kN。

图17 中给出了轮轨的最大von Mises 应力和等效塑性应变与剥离长度的关系。可以看到，轮轨最大von Mises 应力和最大等效塑性应变均随剥离长度的增大而增大。当剥离长度从20 mm增大至50 mm 时，车轮最大von Mises 应力值增加了69.2 MPa，等效塑性应变增加了0.002 7；而钢轨最大von Mises 应力增加了122.4 MPa，等效塑性应变增加了0.009 2，表明剥离长度对钢轨的von Mises 应力和等效塑性应变的影响更显著。

图17 轮轨最大von Mises 应力和最大等效塑性应变与剥离长度的关系Fig. 17 Relationships between the maximum von Mises stress and maximum equivalent plastic strain of the wheel-rail vs. the spalling length

4.3 剥离深度的影响

在列车速度为100 km/h 和2 种剥离长度（= 20，40 mm）工况下，讨论2 种不同剥离深度（= 1，2 mm）对最大轮轨接触力、最大轮轨von Mises 应力和等效塑性应变的影响。图18 为轮对右侧（含踏面剥离和完好车轮）轮轨接触力-时程响应曲线。可以看到，完好车轮工况下的最大轮轨垂向、纵向接触力均小于含踏面剥离的情形；同一剥离长度工况下，不同深度剥离引起的轮轨垂向和纵向接触力时程曲线几乎重合。这表明在剥离长度、剥离宽度、列车速度一定的条件下，剥离深度对轮轨接触力几乎没有影响。这是因为车轮在经过踏面剥离区域时，轮轨接触状态在单点接触与两点接触之间转换时，只与踏面剥离长度和宽度有较大关系，而不会随剥离深度的微小变化而产生显著变化。

图18 不同工况下轮对右侧轮轨接触力时程曲线Fig. 18 Time history curves of the wheel-rail contact forces on the right side of wheelset under different conditions

图19 中分别给出了轮轨最大von Mises 应力和等效塑性应变与剥离深度之间的关系。通过对比含踏面剥离和完好车轮情形，可以发现，当车轮踏面上出现剥离时，轮轨最大von Mises 应力和等效塑性应变显著提升。相同剥离长度下，车轮最大von Mises 等效应力和等效塑性应变均与剥离深度呈正相关。这是由于当剥离长度和宽度一定时，剥离与车轮踏面之间的夹角将完全由剥离深度决定，随着剥离深度的增大，该夹角逐渐变小，进而容易产生较大的应力集中和塑性变形。而随着剥离长度和宽度的增大，该夹角逐渐变大，进而导致较小的应力和塑性变形，剥离深度的影响随之减弱。因此，剥离深度从1 mm 增大至2 mm 时，剥离长度20 mm 引起的车轮最大von Mises 应力提高了43.1 MPa，等效塑性应变增加了0.001 65，大于剥离长度40 mm 的情形。而同一剥离长度工况下，钢轨最大von Mises 应力和等效塑性应变不会随剥离深度的增大发生大幅度变化。

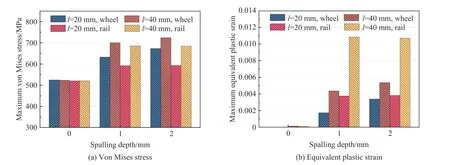
图19 轮轨最大von Mises 应力和最大等效塑性应变与剥离深度的关系Fig. 19 Relationships between the maximum von Mises stress and maximum equivalent plastic strain of the wheel-rail vs. the spalling depth

5 结 论

基于含车轮踏面剥离的三维轮轨滚动接触有限元模型，采用ANSYS/LS-DYNA 有限元程序模拟了踏面剥离引起的轮/轨冲击力学响应，分析了轮轨冲击过程中的轮轨接触力/压力、接触斑及黏滑特性、钢轨表面节点速度分布和应力应变状态等响应特征，讨论了列车速度、剥离长度和剥离深度等关键参数对轮轨冲击响应的影响，得到以下主要结论。

（1）最大轮轨垂向接触力随列车速度的提高先增大后减小，在列车速度为300 km/h 时具有最大值，约为准静态轮轨垂向接触力的1.35 倍；而最大轮轨纵向力随列车速度的提高出现了微小波动，最大值约为稳态轮轨纵向接触力的1.25 倍。

（2）最大轮轨垂向接触力、切向接触力、轮轨最大von Mises 应力和最大等效塑性应变等动态响应与剥离长度均呈单调递增关系。

（3）剥离深度对轮轨接触力、钢轨最大von Mises 应力和最大等效塑性应变几乎没有影响，而对车轮最大von Mises 应力和最大等效塑性应变影响显著。