基于不动点迭代的增广拉格朗日声源识别算法

贺岩松， 贾晨阳， 黄琳森， 昝 鸣， 徐中明

(1.重庆大学 汽车工程学院，重庆 400030； 2. 重庆大学 机械传动国家重点实验室，重庆 400030)

近场声全息是声源识别和声学成像的重要方法之一，其发展和应用十分广泛[1-2]。该方法可以在近场记录得到高空间频率的倏逝波，从而突破瑞利判据的限制，提高声场重建性能。

早在20世纪80年代，Williams等[3-4]就首次提出基于空间傅里叶变换的近场声全息理论，但该方法对声源形状和全息面有诸多限制，且进行傅里叶变换时会产生卷绕误差。为突破该方法的限制，先前学者提出了许多新的方法，如边界元法[5-6]、等效源法[7-9]、统计最优[10-11]等。其中等效源法可以应用于任意形状声源，且拥有鲁棒性好、效率高、易于实现等诸多优点。等效源法主要思想是将实际声源等效为许多虚拟点源的叠加，通过建立声源面到全息面的传递关系，求解得到源强矢量，从而重建声场。在应用等效源法求解逆问题时，会产生不适定性问题，需要对重建过程进行正则化处理。传统方法主要应用L2范数正则化方法，包括Tikhonov正则化[12-13]和截断奇异值分解[14-15]等，该方法主要针对低频声源，对中高频声源声场重建效果较差。

近年来，基于L1范数最小化问题的稀疏正则化方法被逐渐引用到声源识别中。Chardon等[16]首次将压缩感知理论引入近场声全息，并构建近场声全息的稀疏框架。Gade等[17-18]提出宽带声全息(wideband acoustic holography, WBH)，在中高频拥有很好的重建性能，在一定程度上弥补了传统方法的短板，但在低频时对相干声源的识别效果不佳。Fernandez-Grande等[19]在稀疏等效源法的框架下应用CVX工具箱进行求解，在较宽的频率范围内拥有较好的重建精度，但该方法比较耗时，效率不高。张晋源等[20]在传统压缩波束形成的基础上，应用迭代重加权L1范数进行改进，从而有效地提高了声源的空间分辨率和旁瓣衰减能力。Hald[21]阐述并对比五种不同的迭代稀疏等效源法，包括宽带声全息和快速迭代收缩阈值算法(fast iterative shrinking threshold algorithm, FISTA)，并在仿真和试验的基础上，讨论了不同方法的优化选择。樊小鹏等[22]提出分裂增广拉格朗日反卷积声源识别算法，利用交替迭代乘子法求解反卷积问题，显著提高了声源识别精度和计算效率。增广拉格朗日方法(augmented Lagrangian method, ALM)是解决L1范数正则化问题的重要方法，该方法计算效率高，且对惩罚参数有很好的鲁棒性，在压缩感知领域有诸多应用[23-25]。

本文致力于在等效源法的稀疏框架之下，为提高声源识别的频率范围和分辨率，提出一种基于增广拉格朗日方法的声场重建算法；为证明该算法在全频带下的重建性能，仿真时，将该算法与Tikhonov正则化方法，宽带声全息和快速迭代收缩阈值三种算法进行对比，同时检验其对不同信噪比(signal-to-noise ratio, SNR)和全息距离的适应性。最后，通过试验验证该算法的性能。

1 基本理论

1.1 等效源法

等效源法的基本原理如图1所示，其将振动体(声源)产生的声场由一系列等效点源产生的声场叠加代替，而这些等效源的强度可以利用全息面的声压反求得到，从而实现声场重建和声源的准确定位。

如图1所示，假设全息面有M个测量点，等效源面分布有N个虚拟等效点源，则第m个测量点的声压可表示为

(1)

式中：qn为第n个等效源的源强;g(rm,rn)为第n个等效源和第m个测量点之间的声压传递函数，表达式为

(2)

图1 等效源法示意图Fig.1 Schematic diagram of equivalent source method

p=Aq

(3)

式中，q的表达式为q=iρckQ，Q为体积速度向量。通过对式(3)逆向求解可得到等效源强度，并可以重建得到重建面声压，即

pR=Gq

(4)

式中：pR为重建面声压;G为等效源面到重建面的传递矩阵。

考虑到测量成本等因素，实际应用中全息面传声器的数量远远小于等效源的数量，即M≪N，因此，在进行欠定方程的逆向求解时会产生不适定问题。为解决此问题，Tikhonov正则化方法是最为常用的方法之一，其引入L2范数对源强向量进行约束，可表示为

(5)

式中，λ为正则化参数，对其合理选择可以很好地平衡量化误差和源强向量。

当等效源的分布是稀疏或近似稀疏时，对源强向量进行稀疏约束能够更加精确地得出声源信息。理想情况下，可以应用L0范数约束求得等效源强的稀疏解，此时式(5)转化为

(6)

(7)

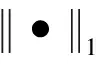
1.2 ALM-FP算法

在压缩感知理论框架下，L1范数正则化方法成为稀疏重建问题的重要方法。本文应用如下L1范数正则化模型求解稀疏重建逆问题，在选择合理的正则化参数的情况下，该问题与式(7)等效

(8)

增广拉格朗日方法对惩罚参数有很好的鲁棒性，且易于求解，同时应用不动点(fixed point, FP)迭代方法求解其子问题，使该算法拥有很好的全局收敛性，因此本文应用该方法解决上述最小化问题。

增广拉格朗日方法求解过程为

(9)

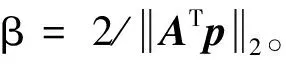
(10)

对于式(10)的拉格朗日最小化问题，我们应用不动点迭代进行求解，令

(11)

则式(10)转化为

(12)

根据文献[26]，该问题求得的结果为

式中:τ为阈值因子，其取值范围为0<τ≤2/λmax，λmax为矩阵ATA的最大特征值，本文令τ=1.8/λmax；∇g(q)的表达式为

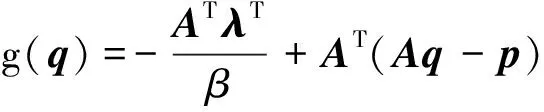
(14)

以上即为ALM-FP算法实现的整个过程，其具体的算法步骤以伪代码形式总结如下：

计算全息面声压p以及传递矩阵A和G

初始化，令λ0=0，q0=0，k=0，阈值因子τ=1.8/λmax。

通过式(14)求得∇g(qk)；

通过式(13)计算qk+1；

通过式(9)更新拉格朗日算子λ；

更新迭代次数k=k+1；

把求解得到的q当作下一步迭代的初始值

End

输出迭代完成得到的最优q值；

重建得到重建面声压;pR=Gq。

2 仿真分析

为验证ALM-FP算法的声场重建性能，对该算法进行相应的仿真分析。仿真时声源、重建面和全息面按照图2(a)布置。定义声速为340 m/s，空气密度为1.29 kg/m3，目标声源采用脉动球源，其半径设为0.01 m，振速为2.5×10-2m/s；设定等效源面和重建面到声源面距离分别为0.001 m和0.02 m，全息距离为0.3 m，等效源面分布有41×41个等效源，网格间距为0.02 m，重建面网格尺寸为0.8 m×0.8 m，网格间距为0.02 m。为保证仿真和试验的一致性，仿真采用36通道圆形随机阵列，阵列点的坐标如图2(b)所示。所有的仿真测试均在Windows10操作系统的电脑(AMD A10-5800K 处理器，3.80 GHz，8.00 GB RAM)上的MATLAB R2016a(64位)中完成。

图2 仿真布置图和传声器阵列Fig.2 Layout diagram of simulation and microphone array

本次仿真分析以单声源和相干双声源两种状况进行分析，以Tikhonov正则化、WBH、FISTA作为新算法的对比研究对象。单声源时，声源位于坐标(0,0,0)m处，即为声源表面的正中心，双声源时，声源的位置分别为(0.2, 0, 0)m和(-0.2, 0, 0)m。另外，为了定量地分析声场重建精度，定义幅值重建误差E1和平均相位误差E2如下

(15)

(16)

式中：pcal为计算得到的重建面声压；pt为重建面理论声压;L为重建面网格点数；pcal,i和pt,i分别为重建面第i个网格点的计算声压和理论理论声压；φ(·)为取相位。幅值重建误差E1和平均相位误差E2越小，表明重建精度越高。

2.1 性能表现

为检验ALM-FP算法的性能，在单声源和相干声源情况下对该算法进行仿真模拟，并与Tikhonov正则化、WBH、FISTA三种方法进行对比。仿真时加入信噪比为30 dB的高斯白噪声，动态显示范围为15 dB。

表1和表2分别展示了四种方法在500 Hz，1 500 Hz以及3 000 Hz三个频率下二维重建面声压云图，其中表1为单声源，表2为相干声源。从表中可以看出，在两种识别过程中， Tikhonov正则化方法在三个频率下的主瓣宽度都比较大，在低频时尤为明显，真实声源无法被准确识别和定位，这主要是由于测点数目较少导致；WBH方法对单声源识别表现良好，在低频时识别相干声源失效，无法识别出两个声源位置。FISTA和ALM-FP两种方法都能得到很好的结果，但相对而言，ALM-FP方法在识别过程中拥有更好的分辨率，而且其最大声压值与理论最大声压最为接近。

表1 单声源重建面声压云图(仿真)Tab.1 Sound pressure maps of reconstruction surface for single sound source(simulation)

表2 相干声源重建面声压云图(仿真)Tab.2 Sound pressure maps of reconstruction surface for coherent sound source(simulation)

三个频率下四种方法的重建面中间行声压对比图，如图3所示。图3(a)～图3(c)为单声源，图3(d)～图3(f)为相干声源。其结果基本印证了上述结论，三个频率下，Tikhonov正则化方法得到的声压值都与理论值相差较大；单声源时，ALM-FP方法与理论值契合度最高，效果最好；相干声源状况下， WBH在低频时基本失效，FISTA和ALM-FP表现良好，同样是ALM-FP方法与理论值更为接近。

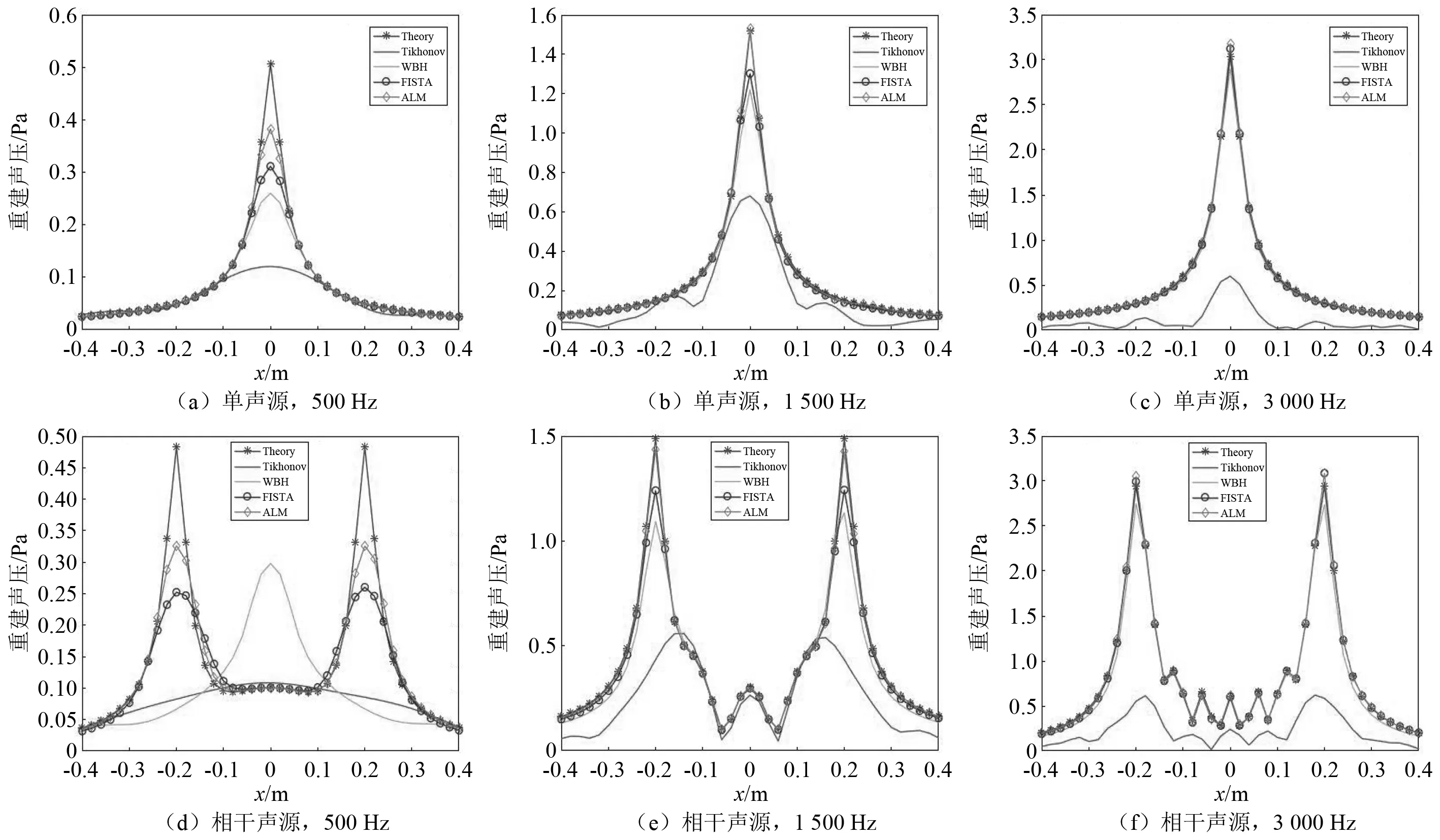
图3 重建面中间行声压Fig.3 Sound pressure in the middle row of the reconstruction surface

表3为相干声源情况下四种算法在1 500 Hz时的计算时间，该结果为十次计算下的平均值，其中FISTA和ALM-FP的迭代次数均为1 000次。从结果可以看出，Tikhonov和WBH算法拥有较好的计算效率，其中WBH计算时间在0.1 s以下，计算效率最高，但两种算法在精度上都有一定的缺陷。FISTA和ALM-FP算法的计算时间分别为21.077 s和10.359 s，相对其他两种算法虽然效率不高，但仍在可接受的范围内，而且，相对FISTA算法，ALM-FP在精度和计算效率上都具有一定的优势。

表3 四种方法计算时间(相干声源1 500 Hz)Tab.3 Computational efficiency comparison of the four methods (coherent sound source at 1 500 Hz)

2.2 误差分析

通过定量地分析算法的幅值误差和相位误差，能够更好的看出算法在全频段下的声场重建性能，改变仿真时的信噪比和全息距离，能够直观的看出各算法对信噪比以及测量距离的适应性。

图4分别展示了单声源和相干声源两种情况下，从200～4 000 Hz四种算法的重建面幅值误差曲线。每条曲线每隔50 Hz取一个频率点，单个频率的误差计算10次以取得平均值。单声源时，Tikhonov正则化算法在低频时的幅值重建精度要优于中高频，但整体上重建误差在35%以上，相对其他算法表现较差。WBH、FISTA和ALM-FP三种算法均有比较好的幅值重建精度，重建误差均在20%以下，且中高频的重建效果要好于低频。ALM-FP算法整体上的重建误差在10%以下，相对其他算法在低频的重建误差更小，对低频单声源声场重建更有优势。双声源时，Tikhonov正则化算法与单声源时表现类似。WBH算法的曲线上存在一个明显的转换频率，在转换频率以下的低频时出现较大的重建误差，大于转换频率时，重建误差较小。FISTA和ALM-FP依然拥有较高的幅值重建精度，相对WBH和Tikhonov正则化优势明显，但整体上而言，特别是在低频时，ALM-FP算法拥有更小的重建误差，在进行声场重建时效果更好。

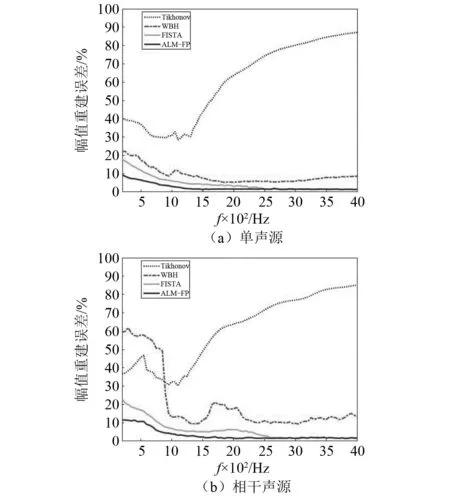
图4 声压幅值重建误差曲线Fig.4 Curves of source pressure amplitude reconstruction error

为了进一步分析算法的重建性能，以相干声源为例，图5给出了四种算法在1 500 Hz时的重建面网格点的相位以及四种算法在200～4 000 Hz频率段的平均相位误差，由于重建面网格点较多，随机选取连续的100个点为代表以体现重建声压的相位情况。可以发现，Tikhonov正则化算法重建得到的声压相位与理论相位有较大的偏移，相位的重建效果较差，其他三种方法得到的结果与理论结果有相同的走势，其中WBH有些许的偏移，FISTA与ALM-FP能够与理论曲线很好的契合，说明其能够得到很好的相位结果。通过平均相位误差曲线可以看出，与相干声源幅值误差曲线有相似之处，Tikhonov正则化算法会产生较大的相位误差，特别是中高频段。WBH低频相位误差较大，高于转换频率时效果较好。FISTA与ALM-FP在整个频段都有较小的相位重建误差，FISTA算法误差略小一点，但整体而言，两种算法均表现出很好的相位重建性能。

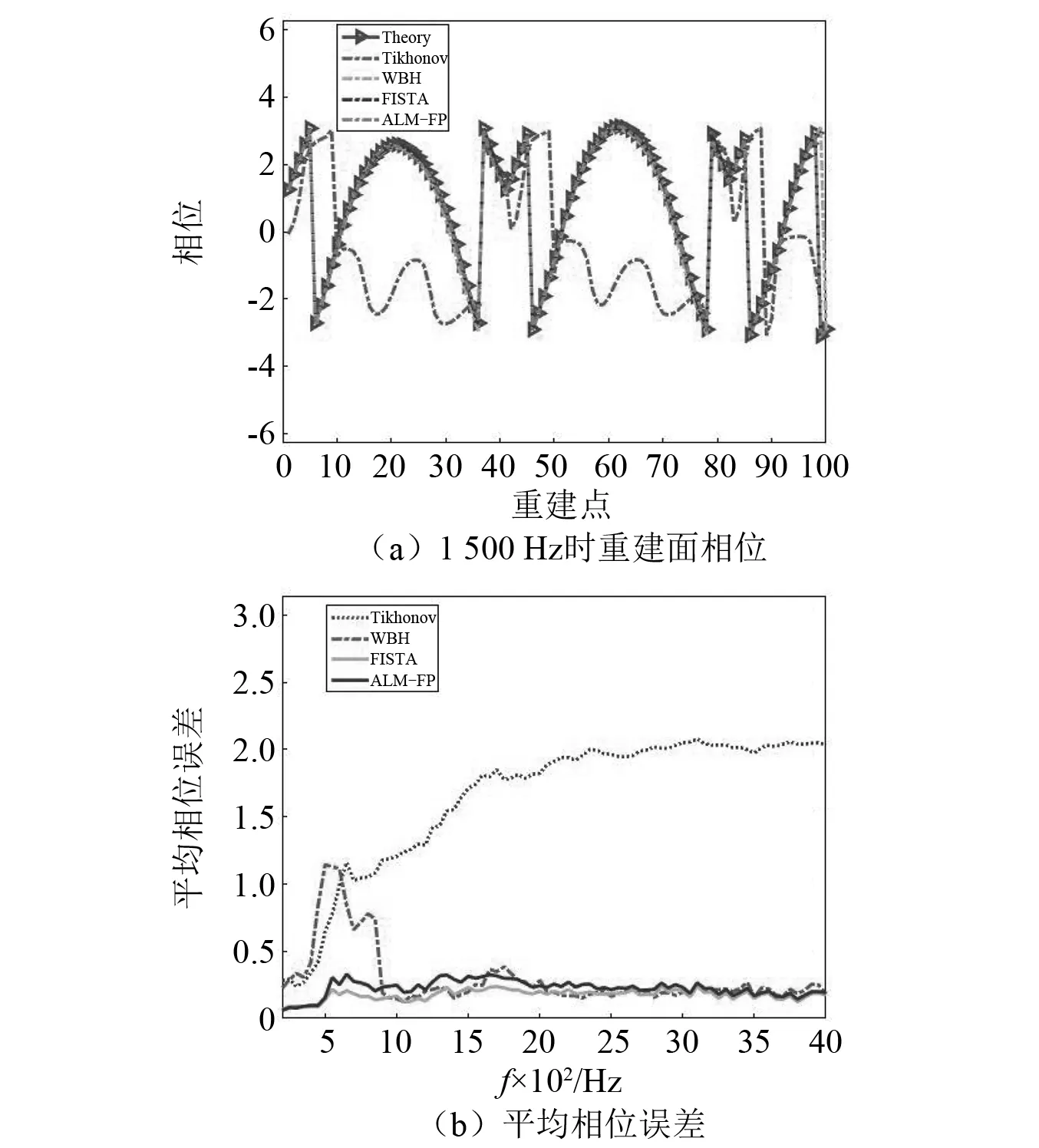
图5 相位分布及相位误差Fig.5 Phase distribution and phase error

通过算法在单双声源的重建面幅值误差曲线可以发现，不同频率时，当单声源重建较好时，双声源的重建效果并不好，在相干双声源情况下，对算法的要求更苛刻，因而该情况下，也更能反映算法对信噪比和全息距离的适应性。四种方法在不同信噪比的情况下的重建误差云图，如图6所示，信噪比范围为10～60 dB，全息距离为0.3 m。四种方法在不同全息距离下的重建误差云图，如图7所示，全息距离范围为0.05～0.50 m，信噪比为30 dB。两图均在相干声源情况下计算所得，图中颜色条的范围为0～100 %。

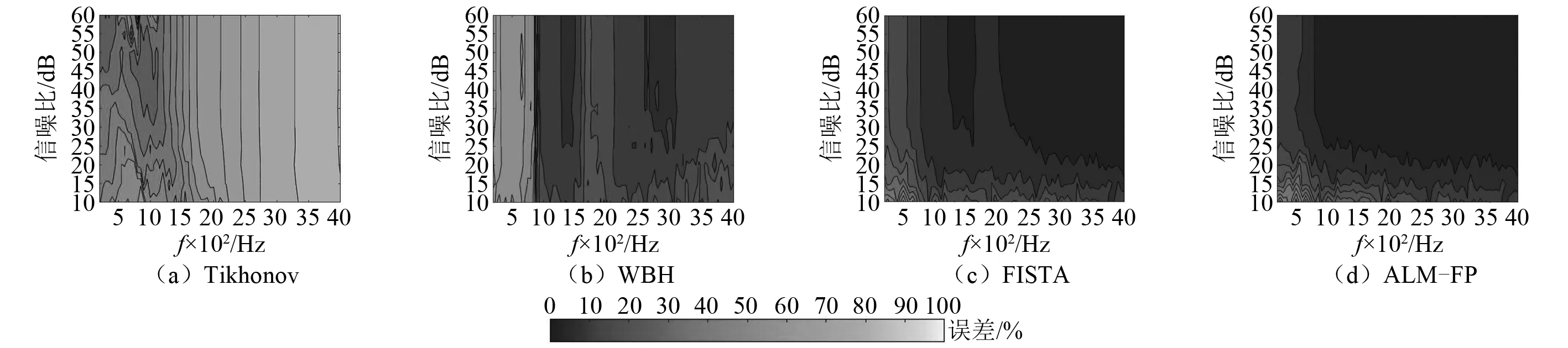
图6 不同信噪比下各方法的重建误差云图Fig.6 Reconstruction error map of methods with different SNR

图7 不同全息距离下各方法的重建误差云图Fig.7 Reconstruction error map of methods with different hologram distance

从图6可以看出，Tikhonov正则化方法在低频重建效果优于中高频，且中高频时基本失效，低频时，信噪比较高时的重建误差较小。WBH方法在低频失效，在中高频对信噪比的适应性较好，在不同信噪比下都有比较好的重建效果。FISTA与ALM-FP两者有相似的趋势，但ALM的整体效果更好，其重建误差随频率升高和信噪比增大而减小，只在频率小于800 Hz、信噪比小于15 dB时，重建误差较大。

从图7可以看出，全息距离的减小有利于声场重建的效果。图7(a)为Tikhonov正则化方法，通过减小全息距离，其重建误差可以减小为原来的一半。另外减小全息距离可以拓宽WBH方法的频率范围，在全息距离较小时，WBH在低频时也可以有较好的重建精度。ALM-FP方法对全息距离有较好的适应性，在不同全息距离下，都有比较好的重建精度，只在全息距离接近0.5 m的低频时，有较大的重建误差。FISTA方法整体上在不同全息距离下有比较好的重建精度，但频率适用性上要劣于ALM-FP方法。

3 试验验证

验证算法性能的试验布局图如图8所示，将单频信号激励的音响作为声源，采用B & K公司、直径0.65 m的36通道扇形轮阵列测量声压信号，阵列集成4958型传声器，各传声器测量的声压信号经PULSE 3660D型数据采集系统同时采集并传输到PULSE LABSHOP中进行数据分析，信号采样频率为32 768 Hz，将得到的数据在MATLAB软件中进行计算，得到重建面声压云图。图8(a)为单声源布局，声源坐标为(0, 0, 0)m，图8(b)为相干声源布局，声源坐标为(0.2, 0, 0)m、(-0.2, 0, 0)m，声源与阵列之间的距离均为0.2 m，其他参数设置与仿真时相同。

图8 试验布局图Fig.8 Layout of experiment

与仿真相对应，表4和表5分别展示了试验时单声源和相干双声源在500 Hz，1 500 Hz和3 000 Hz三个频率下的重建面声压云图，其结果能很好地验证仿真的结论。单声源时，但是Tikhonov正则化方法虽然能识别到噪声源的位置，但是出现较多的鬼影，而且主瓣较大，分辨率很低。WBH、FISTA和ALM-FP三种方法能比较好识别噪声源的位置，且随着频率的升高，声源主瓣变小，分辨率变好，但整体上特别是在低频条件下，ALM-FP较其他两种方法有更好的分辨率，与仿真的结果相对应。相干双声源情况下，Tikhonov正则化方法出现较多的旁瓣和鬼影，基本无法判别噪声源的位置，声源识别效果很差。WBH方法在低频时失效，将两个声源识别成为中间的一个声源，在中高频能很好地识别噪声源的位置。FISTA和ALM-FP两种方法能很好地识别噪声源的位置，不过会出现一些微小的旁瓣，原因可能是由于试验是在普通室内进行的，壁面的声波反射无法避免，从云图的结果来看，ALM-FP方法在三个频率下的分辨率更高，而且能够更好地消减旁瓣，效果更好。

表4 单声源重建面声压云图(试验)Tab.4 Sound pressure maps of reconstruction surface for single sound source(experiment)

表5 相干声源重建面声压云图(试验)Tab.5 Sound pressure maps of reconstruction surface for coherent sound source(experiment)

4 结 论

基于等效源法和压缩感知理论，本文提出一种基于增广拉格朗日方法的声源识别算法ALM-FP，并给出了该方法的理论推导，模拟仿真了单声源和相干双声源情况下的声源识别成像效果和随频率变化的误差曲线，给出了不同信噪比和全息距离下的重建误差云图，最后通过试验验证了仿真结果。

通过仿真和试验结果表明，ALM-FP算法能够在较宽的频率范围内进行准确的声源识别和声场重建，对比其他三种方法，该方法拥有更好的重建精度，声源识别分辨率更高，特别是在低频区域，其优势更加明显。另外该方法对信噪比和全息距离拥有很好的适应性，但是在测量环境特别恶劣时，比如低频时信噪比很小或全息距离很大，会严重影响该方法的重建效果，产生较大的重建误差。