输电线路防舞电涡流阻尼器参数优化试验研究

楼文娟， 黄赐荣， 陈思然

(浙江大学 结构工程研究所，杭州 310058)

导线舞动对线路的危害极大，容易造成混线短路、闪络跳闸、导线磨损、线路金具损坏、间隔棒断裂等问题，甚至引发断线、倒塔等恶性事故[1]，对输电线路的安全运行构成重大威胁。随着国家电网规模的日益扩大，舞动防治尤为重要[2]。

目前国内外所采用的防舞技术按防舞原理可以分为三类：气动式防舞装置、结构式防舞装置、阻尼式防舞装置。气动式防舞装置通过改变覆冰导线气动特性来抑制舞动，目前气动式防舞装置主要有扰流线、回转式间隔棒等等。楼文娟等[3]通过计算流体力学(computational fluid dynamics，CFD)模拟和风洞试验对装有扰流线的导线气动力特性进行了研究并证实了扰流线的防舞效果。金成生[4]基于舞动稳定性机理提出了可以有效抑制舞动的线夹回转式间隔棒，且其防舞效果已在日本实际运行的线路上得到了验证。结构式防舞装置通过提高线路动力稳定性来抑制舞动，常见的结构式防舞装置主要有失谐摆、双摆防舞器、相地间隔棒等等。失谐摆通过调整导线扭转频率来使之与竖向频率分离，从而防止导线发生竖-扭耦合舞动。孙珍茂等[5]推导了安装有失谐摆的覆冰单导线简化模型的非线性舞动方程，并利用数值方法验证了失谐摆防舞器能有效抑制导线舞动。杨晓辉等[6]对传统的双摆防舞器提出了改进方案，并采用数值方法对试验线路上双摆防舞器的防舞效果进行了验证。卢明等[7-8]研制了一种新型防舞装置-相地间隔棒，通过真型线路试验、数值模拟等手段对该装置的防舞性能进行了验证，并提出了该装置的最优配置方案。虽然拉线式相地间隔棒可以有效地降低舞动幅值，但依然会存在次档距振荡、装置安装空间占用大、相地间隔棒与导线连接处的内力较大等问题，值得后续改进设计。目前，气动式和结构式防舞技术的相关研究已经相对成熟，但阻尼式防舞技术在输电线路中应用相对较少，典型的阻尼式防舞装置有黏弹性阻尼相间间隔棒。Lou等[9]对传统的相间间隔棒进行了改进，用黏弹性阻尼相间间隔棒替代相间间隔棒，并用多尺度方法求解运动方程，研究了相间高差、相间荷载差异、相间张力差等参数对舞动防治效果的影响，验证了黏弹性阻尼相间间隔棒的良好防舞性能。输电线路发生舞动的本质是导线的气动负阻尼比的绝对值大于结构自身阻尼比，所以通过阻尼器提供附加阻尼来提高导线系统的结构阻尼比可以从根本上解决导线舞动问题。目前在桥梁拉索相关研究中，已经被证明拉索近端部安装阻尼器可以有效提高拉索系统的阻尼比[10-11]，发挥良好的减振效果，但在输电线路的防舞研究中，类似的阻尼器减振技术缺乏必要的试验验证和理论分析。

现有研究表明导线舞动形式以竖向、竖-扭耦合舞动为主，针对此现状，本文针对竖向舞动及竖-扭耦合舞动提出了一种新的阻尼式防舞方案，通过在靠近输电塔的位置设置阻尼器减振耗能来达到预期的防舞要求，以某1 000 kV输电线路为工程原型，设计了缩尺比为1∶17的室内大比例缩尺试验模型，通过输电导线-电涡流阻尼器系统的自振试验测定系统的等效阻尼比，对电涡流阻尼器的安装位置、内刚度、阻尼系数以及导线初始张力等参数对导线系统的一阶竖向等效阻尼比的影响进行了研究；并结合运动方程特征值分析以及ANSYS仿真模拟，在自振试验所确定的阻尼器最优参数下对原型线路设置阻尼器前、后的舞动情况进行了对比分析，验证了本文提出的阻尼式防舞方案具有良好的防舞性能。

1 试验模型设计及标定

试验线路是以某1 000 kV八分裂输电线路工程项目为原型，档距为276 m，两端支座高差为0，子导线选用LGJ-500/45型钢芯铝绞线(直径30 mm)，导线覆冰形状选择D型覆冰，模型设计时已考虑覆冰的质量，具体覆冰形状以及覆冰厚度参考文献[12]。由于八分裂导线简化为等效单导线对系统的竖向阻尼比的影响很小，因此试验设计过程中将八分裂覆冰导线模型等效为一根，即相应导线模型的张力、线密度以及拉伸刚度均放大8倍。两侧固定端采用预紧螺栓装置来调整导线的张力，电涡流阻尼器对称设置在两侧靠近固定端的位置。通过电涡流阻尼器的相对变形和相对速度给导线系统提供附加阻尼，达到提高导线系统的等效阻尼比的作用。试验模型示意图如图1所示，主要包括：导线模型、电涡流阻尼器、高精度工业相机、动态应变仪、张力传感器等，其中高精度工业相机用于测试导线自振过程中的位移响应，动态应变仪同步采集试验过程中导线张力以及阻尼器对导线的作用力。试验中采用人工激振，首先在导线跨中位置悬挂额定质量的重物使导线发生一定位移，然后突然卸载重物实现导线模型的自由衰减振动。

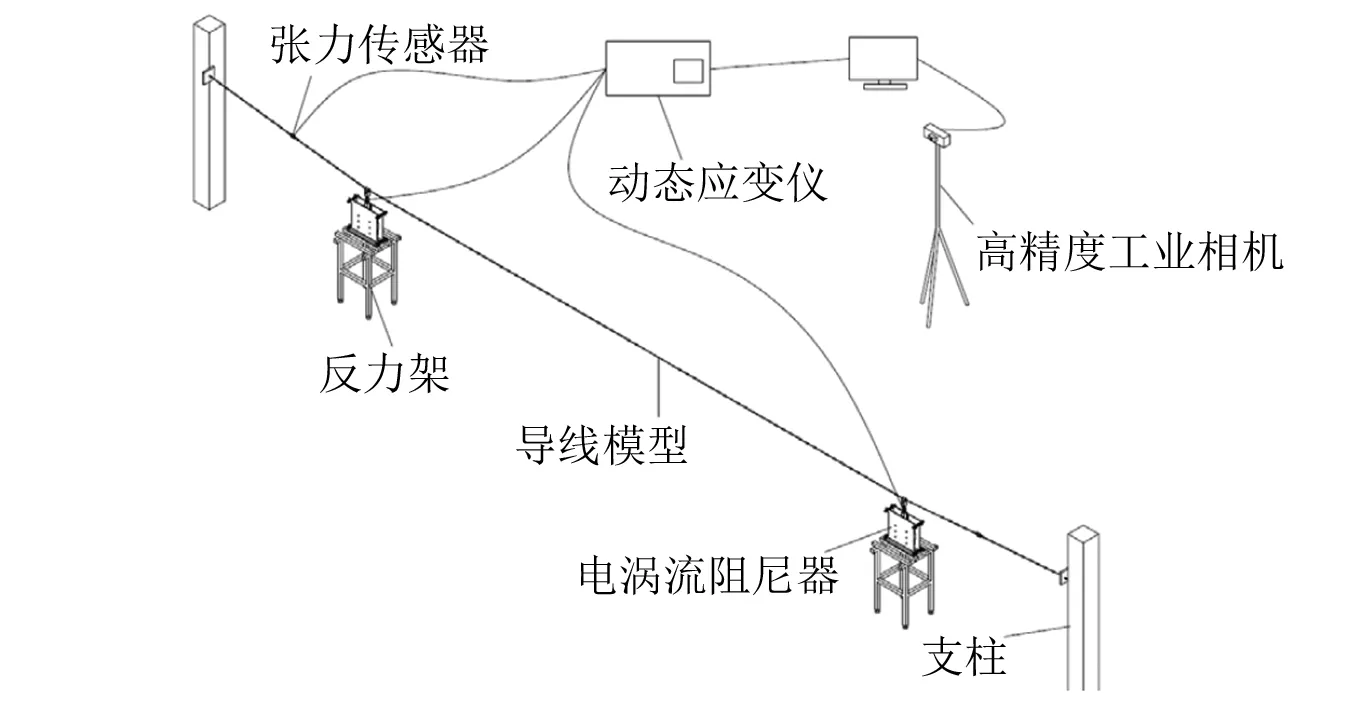
图1 试验模型布置示意图Fig.1 Layout of test model

1.1 输电导线设计

本试验输电导线采用7×7钢丝绳进行模拟，按照缩尺比λl=1∶17设计导线模型。采用钢丝绳模拟导线轴向刚度，再辅以穿过钢丝绳的配重块来实现模型与原型之间的线密度相似，配重块的侧面安装了两个用于固定位置的螺栓防止试验过程中配重块沿钢丝绳发生滑动。导线模型其他相似参数基于动力相似关系通过量纲分析确定，各参数具体数值如表1所示。制作完成的整档导线缩尺模型如图2所示。

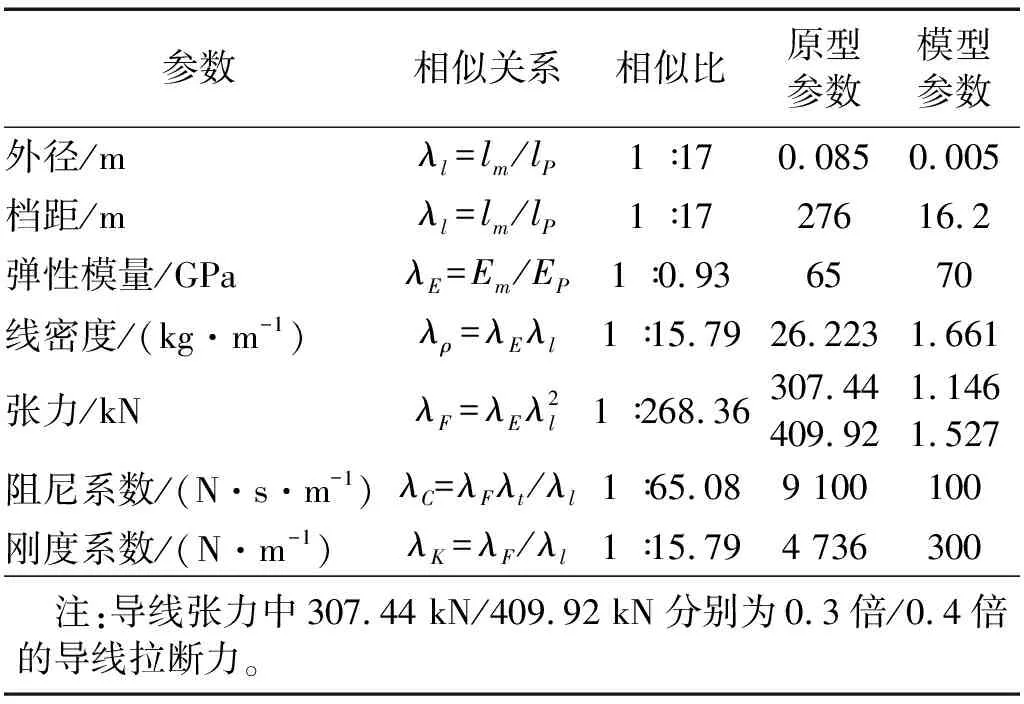
表1 模型物理参数相似比及其参数值Tab.1 Similarity ratio and values of model parameters

图2 导线试验模型Fig.2 Test model of conductor

1.2 电涡流阻尼器工作原理及设计

由于电涡流阻尼器在减振过程中导体板不与磁体直接接触，是一种没有摩擦和磨损的理想阻尼方式，与传统的油阻尼器等相比，具有耐久性好、阻尼系数易调节的优点，因此本文试验中的阻尼器采用电涡流阻尼器。电涡流阻尼是基于电磁感应原理的一种阻尼单元，在低速时可以视为一种理想的线性黏滞阻尼。如图3(a)所示，由楞次定律可知，当导体板在磁场中做切割磁感线运动时，导体板内的磁通量发生变化，会在导体板内产生电涡流，涡电流磁场与原有磁场发生相互作用，会产生一个阻碍导体板运动的安培力，即电涡流阻尼力。在导体板运动过程中，导体板的动能先转化为电能，通过安培力做功，将导体板内的电能转化为热能，从而耗散导线振动时的动能。

如图3(b)所示，本次试验所用电涡流阻尼器由永磁体提供磁场，永磁体通过两块不锈钢钢板及螺栓装置进行固定，在磁体和导体板背部设置高磁导率的导磁板，可以最大限度减小磁路的磁阻和漏磁，有效地解决损耗问题。为了方便试验过程中阻尼器安装及参数调整，阻尼器将竖直放置在与地面固定的反力架上，由于电涡流阻尼器中导体板的面积需远大于磁场的面积，综合考虑导体板的质量及导电率因素，导体板采用铝板，导体铝板通过导体板固定杆与拉力传感器固定连接，张力传感器通过轻质连接件与导线模型进行连接，导线模型在振动过程中带动导体铝板上下振动切割磁感线，由安培力提供阻尼力，通过阻尼力做功，将导线振动的动能转化为热能，从而耗散导线振动时的动能。通过调节永磁体间距和导体铝板的厚度可以调节电涡流阻尼器的阻尼系数。电涡流阻尼器的安装方式和位置见图3，为了提供足够的阻尼系数，每个电涡流阻尼器采用6对75 mm×75 mm×25 mm的永磁体来提供磁场，永磁体的表磁强度为0.4 T左右，导体铝板选择2块15 cm×35 cm的铝板。

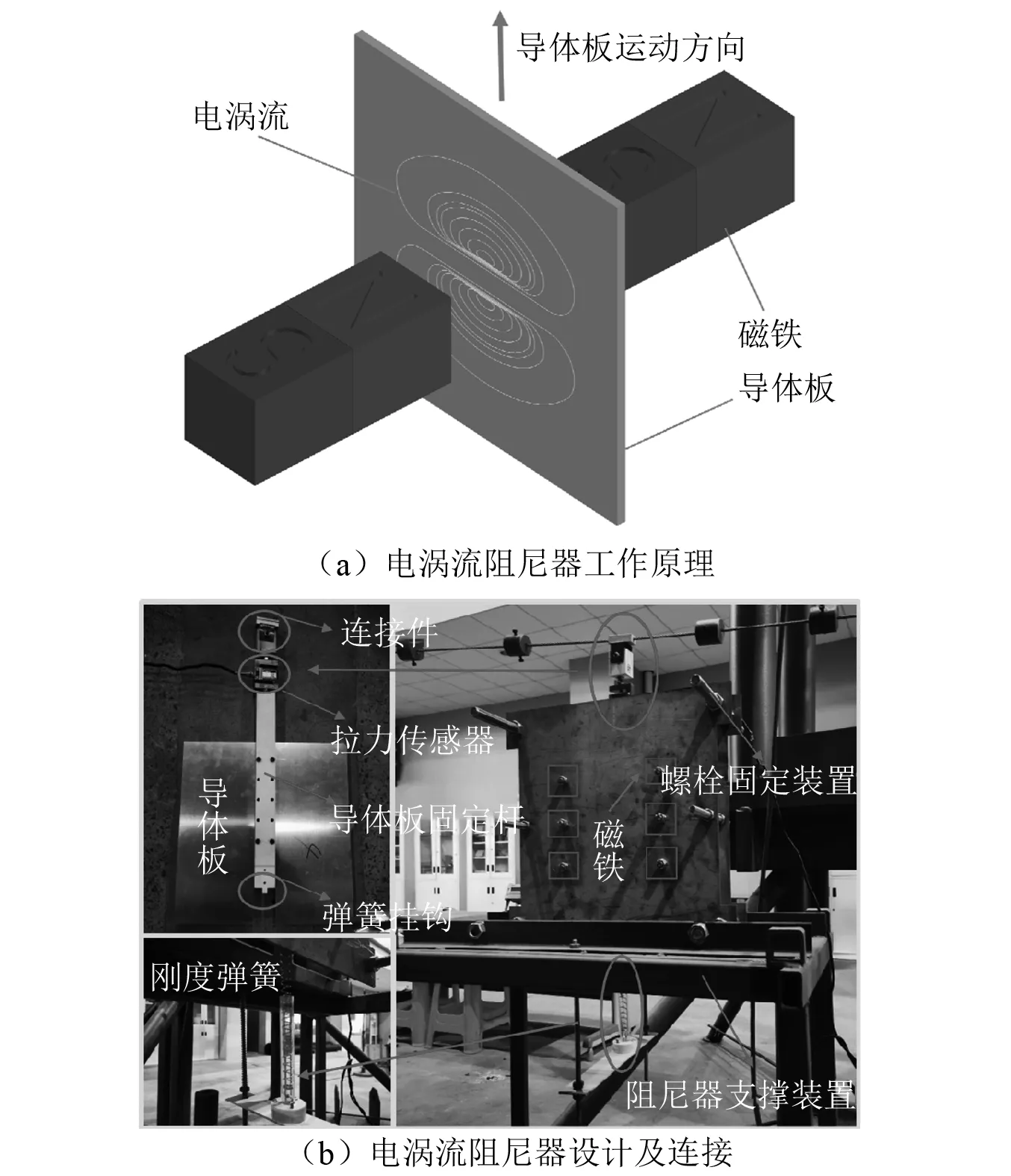
图3 电涡流阻尼器原理及设计安装Fig.3 Installation position of eddy current damper

本文所使用的电涡流阻尼器由阻尼单元和刚度单元构成，其中阻尼单元主要包括永磁体和导体铝板，在低速时可以视为一种理想的黏滞阻尼单元，刚度单元采用定制轴向拉压弹簧进行模拟，弹簧的劲度系数即为阻尼器的刚度系数。弹簧外侧设置塑料管约束弹簧的运动，以避免弹簧压缩时发生屈曲。假设导体铝板的电阻率为φL且磁导率很小，永磁体的长宽尺寸为Lm×am，假定一对永磁体异名磁极近距离相对可以近似形成匀强磁场，磁感应强度为B，与导线模型相连的导体铝板的厚度为bL，以相对速度wr切割磁感线。取一个导体铝板微元，其动生电动势dε可以表示为

dε=Bwrdam

(1)

内电阻dRm为

(2)

当导体板的面积远大于磁场的面积时，可以假定该微元电路的外电阻等于内电阻，则电涡流强度dI为

(3)

该微元受到安培力dFm为

(4)

本次试验中电涡流阻尼器的阻尼系数由N对永磁体所提供，在N对永磁体作用下，导体铝板受到电涡流阻尼力Fm为

(5)

铝的电阻率φT=2.9×10-8Ω·m。

由阻尼力和相对速度的关系可以得到阻尼器的阻尼系数为

(6)

1.3 导线线型及模态验证

为了保证导线缩尺模型在自质量和配重作用下线型的正确性，对缩尺试验模型3个特殊点位处的弧垂采用激光测距仪进行测量，并与理论弧垂进行对比，线型最大误差不超过0.84%(如表2所示)。

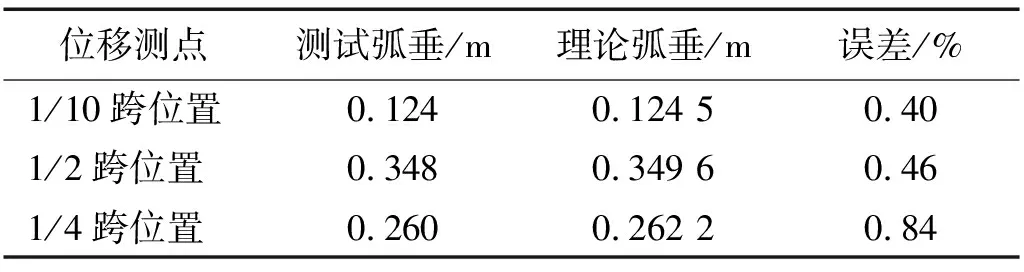
表2 测试弧垂与理论弧垂对比Tab.2 Comparison of measured sag and theoretical sag

在确定线型的基础上，采用单目视频识别技术对测点处的自振位移变化进行实测，并进行频谱分析，验证缩尺模型的设计频率与测试频率是否吻合。根据频谱分析的结果可知，测试频率与设计频率吻合，最大误差不超过0.87%(如表3所示)。

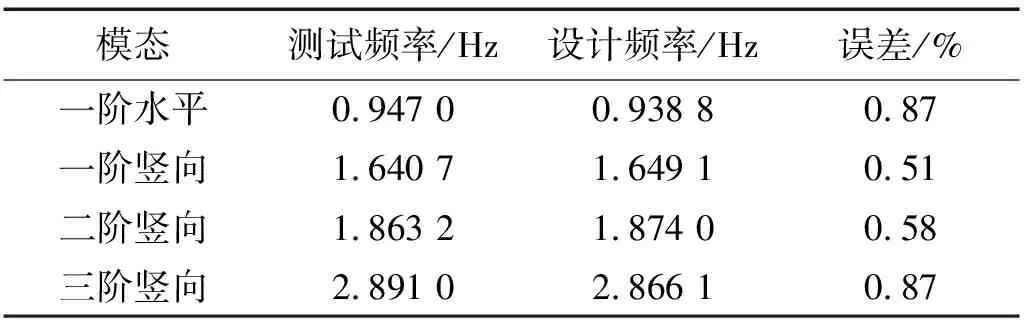
表3 模型测试频率与设计频率对比Tab.3 Comparison of test frequency and design frequency

2 试验工况及结果分析

输电线路发生舞动的本质是气动阻尼比的绝对值大于结构自身阻尼比，即导线的总阻尼比小于零是舞动的必要条件。现有研究表明：在一般情况下输电线路一阶竖向舞动起舞风速相比高阶竖向舞动更低，导线更容易先激发出一阶舞动，且一阶舞动的最大幅值也会比高阶舞动更大，会对线路产生更严重的危害；其次拉索结构靠近端部设置阻尼器对系统高阶模态阻尼比的提升效果相比一阶模态更突出，高阶模态阻尼比甚至可以达到15%以上，足以抑制导线高阶模态舞动，且高阶模态阻尼比对线路的垂度、自质量等结构参数变化的敏感性较低，因此本次试验选择导线-阻尼器系统的一阶模态阻尼比作为防舞效果评价指标，即导线-阻尼器系统的一阶等效阻尼比越大，阻尼器减振效果越好，导线-阻尼器系统越难激发舞动。通过在模型跨中位置悬挂额定质量的重物，突然卸载重物进行导线自由振动试验，选取模型1/4跨位置为单目视频测试技术位移标记点，利用单目视频识别技术实测导线缩尺模型的自由振动位移时程。通过改变电涡流阻尼器的阻尼和刚度系数、阻尼器的安装位置以及导线初始张力对阻尼器的减振效果进行变参数试验研究。由于导线自振过程中存在多阶模态的混合，无法直接得到单一模态振动位移，需要对实测位移数据进行滤波处理获取导线竖向一阶振动位移分量。

2.1 试验工况

为了研究电涡流阻尼器的阻尼系数、刚度系数、阻尼器的安装位置以及导线初始张力对其减振效果的影响，本文对如表4所示的试验工况进行了试验研究，表4中的数据以20～200@20为例，表示参数的研究范围为20～200，参数变化间隔为20，对部分特殊工况会进行阻尼系数加密试验。

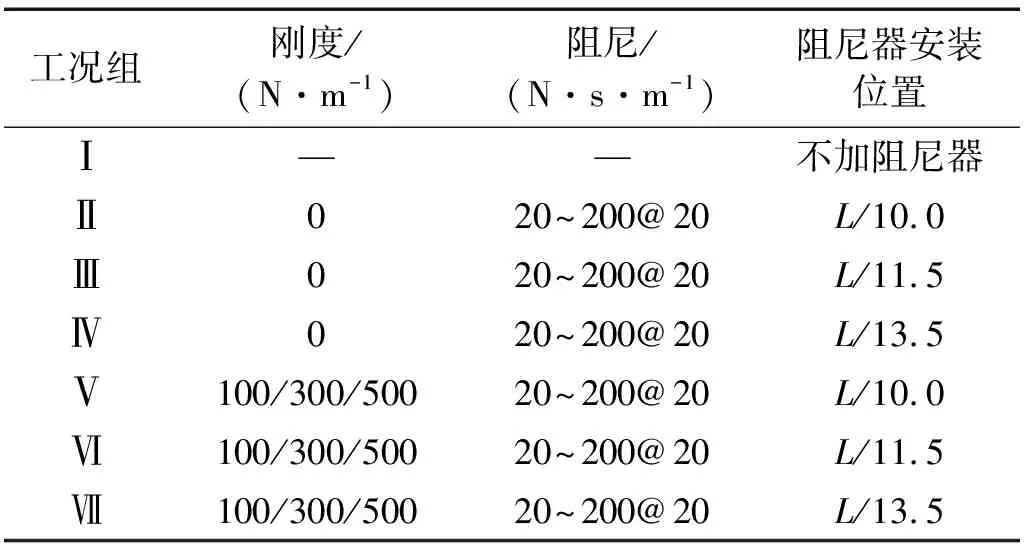
表4 模型试验工况表Tab.4 Test condition of model

2.2 瞬态响应测试与分析

依次按照1.2节中的7组工况进行输电导线-电涡流阻尼器系统的自由振动试验，可获得各组工况下位移测点处的位移响应、阻尼器对导线作用力的时程响应。图4(a)给出了安装阻尼器前、后输电导线模型自振位移曲线对比图，可以看出安装阻尼器后导线自振衰减加快，系统的等效阻尼比提升非常明显。为了精确求得系统的等效阻尼比以方便后续对比研究，以导线安装阻尼器前的自振响应时程为例，对视频测试技术实测的位移响应进行滤波处理，得到导线竖向一阶的振动位移响应A(t)。图4(b)即为安装阻尼器前导线模型自振实测曲线及经过滤波处理提取的一阶竖向自振时程曲线；然后选取一段时间对滤波处理后的位移信号A(t)进行Hilbert变换处理，再对A(t)的对数曲线进行线性拟合，即可识别得到系统的自振频率以及一阶模态阻尼比。图4(c)为滤波处理后的位移响应A(t)的对数曲线及其线性拟合曲线，根据图4(c)的拟合结果得到原始输电导线的一阶竖向结构阻尼比为0.217%左右，与实际线路的阻尼比情况较为符合。其他不同工况下系统的等效阻尼比可根据上述处理方法识别得到。

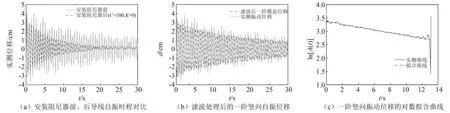
图4 导线模型自振位移时程Fig.4 Time history of natural vibration displacement of conductor model

2.2.1 阻尼器安装位置研究

为了研究阻尼器安装位置对系统阻尼比的影响，本次试验选择在离两端固定柱1.62 m(L/10.0)，1.41 m(L/11.5)，1.20 m(L/13.5)3个位置处对称安装电涡流阻尼器来研究阻尼器位置对阻尼器减振效果的影响，导线张力取0.4倍导线拉断力，暂不考虑阻尼器内刚度的影响，取K=0。图5绘出了阻尼器安装在不同位置处自振试验所得到的导线系统的一阶等效阻尼比结果。

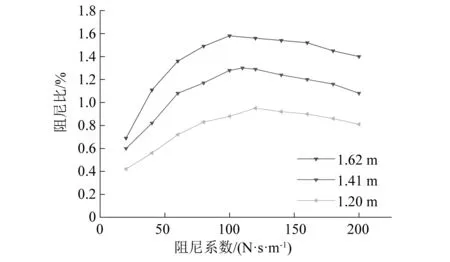
图5 系统一阶阻尼比随阻尼器位置的变化Fig.5 First-order damping ratio of system with different damper installation positions

由图5可知，当阻尼器安装在不同位置时，系统等效阻尼比随阻尼系数变化的趋势基本相似，随着阻尼系数的增大，等效阻尼比呈现先增大后减小的趋势，且存在一个最优的阻尼系数Copt使系统的阻尼比达到最大值ξmax。随着阻尼器的安装位置越大，系统的最大阻尼比ξmax会呈现增大的趋势，最大阻尼比ξmax所对应的阻尼器最优阻尼系数Copt会呈现减小的趋势。可以发现在离两端固定柱1.62 m(L/10.0)的位置对称安装阻尼器，导线系统的等效阻尼比最大可以达到1.54%左右，阻尼器对系统阻尼比的提升效果非常明显。

2.2.2 阻尼器的刚度、阻尼参数研究

阻尼器的减振效果和其附属参数(刚度系数、阻尼系数)有很大的关系，选择合理的阻尼器参数对于线路抑舞减振尤为重要。为了研究阻尼器参数对系统等效阻尼比的影响，本次试验选择在离端部1.62 m(L/10.0)安装电涡流阻尼器，导线张力取0.4倍导线拉断力，通过改变电涡流阻尼器阻尼系数以及刚度系数来进行参数研究。图6绘出了安装不同刚度、不同阻尼的阻尼器时，导线系统的一阶阻尼比的变化情况。由图6可知，当阻尼器刚度保持一定时，系统阻尼比会随着阻尼器阻尼系数的增大呈现先增大后减小的趋势，且存在一个最优的阻尼系数Copt使系统的等效阻尼比达到最大值ξmax；随着阻尼器刚度的增大，系统的最大阻尼比ξmax会减小，最大阻尼比ξmax所对应的最优阻尼系数Copt也会更大，刚度的存在对于阻尼器发挥减振耗能效果是不利因素。

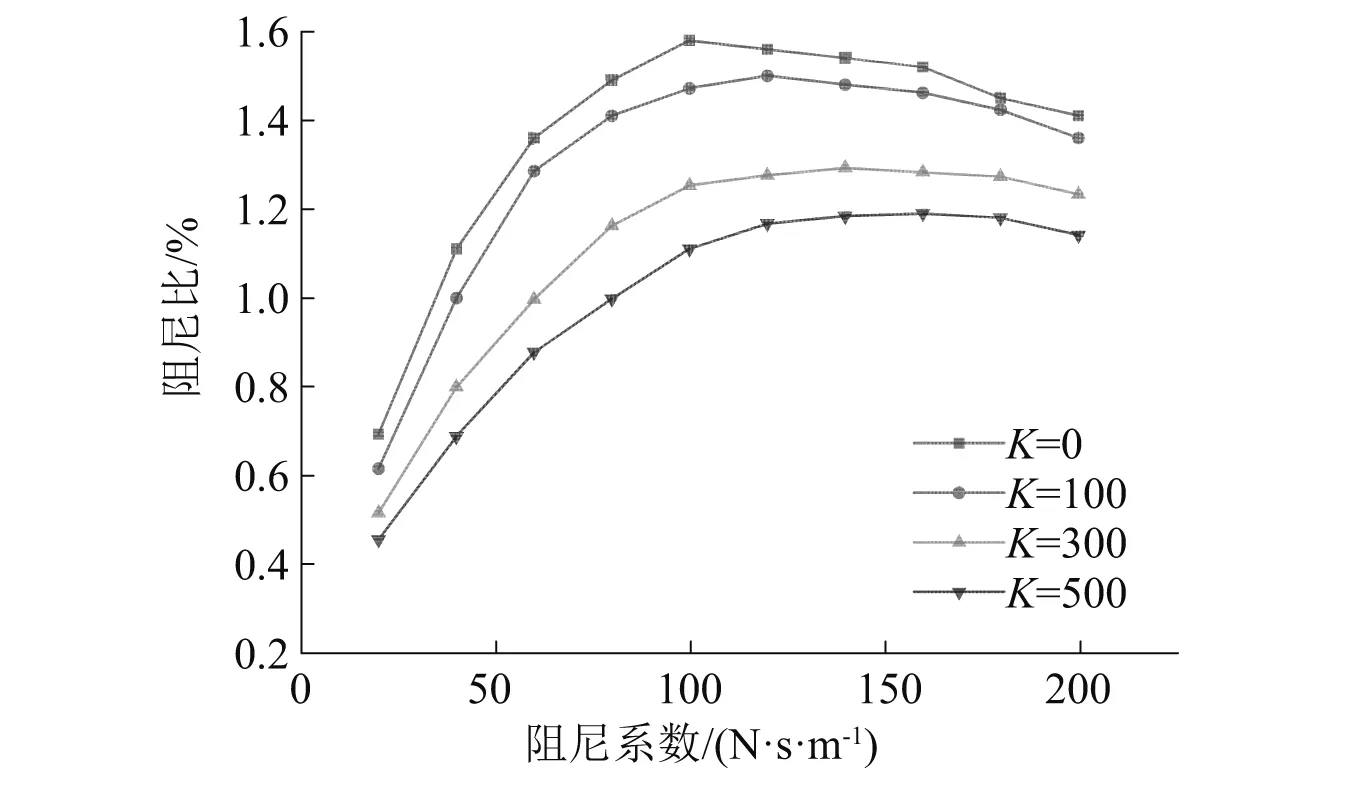
图6 不同阻尼器参数下的系统一阶阻尼比Fig.6 First-order damping ratio of system with different damper parameters

阻尼器对导线的作用力对于阻尼器持续发挥减振作用和系统安全性至关重要，图7给出了安装不同附属参数的阻尼器时，阻尼器对导线的最大作用力Fmax随阻尼器阻尼系数的变化情况。由图7可知，随着阻尼系数的增大，Fmax的变化趋势并不会和等效阻尼比的变化趋势保持一致性，会呈现近似线性增长的趋势。当阻尼系数大于Copt时，系统的等效阻尼比呈现下降趋势，而阻尼器对导线的最大作用力则依然保持上升趋势，对阻尼器发挥防舞性能和装置的安全性来说都更为不利，因此综合考虑在Copt附近选择阻尼器的阻尼系数为最优选择；另一方面，阻尼器内刚度的存在对于阻尼器的减振是非常不利的[13]，内刚度越小，阻尼比提升效果越好，且Fmax也会更小，对阻尼器的减振防舞性能以及系统安全性都更为有利。

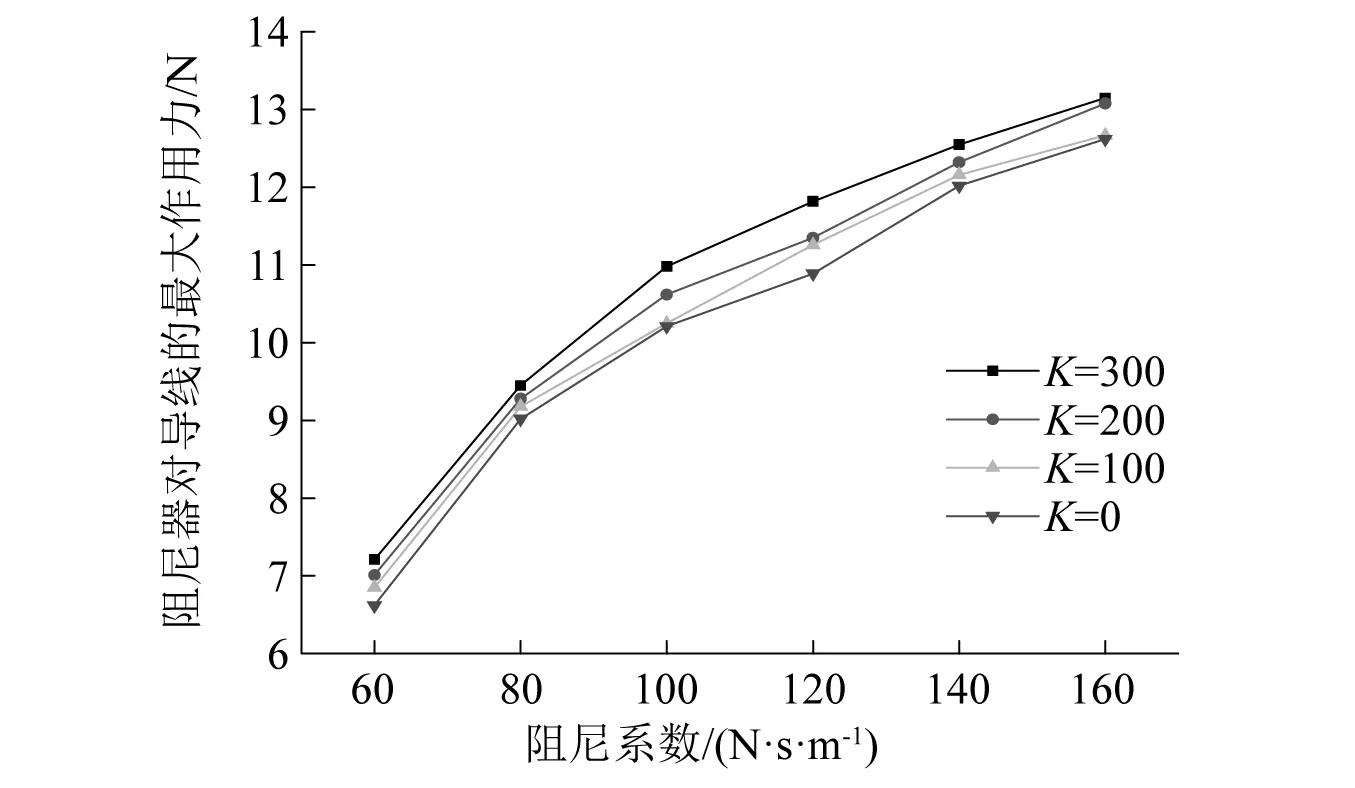
图7 阻尼器对导线的最大作用力Fig.7 Maximum force of damper acting on conductor under different damper parameters

电涡流阻尼器的尺寸和质量是该装置后续推广应用的主要限制因素，为了使电涡流阻尼器的质量、尺寸达到工程可应用的水平，可以通过合理的磁场方向交替分布、稀土高强度磁铁和导磁板的使用来减少所需磁体的数量，从而极大减小阻尼器的尺寸和质量；其次，可以选择将阻尼器与地面或者输电塔塔臂进行可靠连接固定，导体板通过绝缘杆件与导线连接，来进一步减小阻尼器的自质量、尺寸对其减振效果的影响。所以在该防舞装置的实际工程应用中，需要综合考虑等效阻尼比提升，线路系统的安全性以及阻尼器实际制作难度、成本等各方面因素，选择最优的阻尼-刚度参数组合。

2.2.3 导线初始张力研究

阻尼器的减振效果对导线的自身结构属性依赖性较大，为了研究导线初始张力对系统阻尼比的影响，本次试验选择在离端部1.41 m(L/11.5)安装阻尼器(暂不考虑阻尼器内刚度的影响，即K=0)，通过两端固定柱的预紧螺栓装置改变导线初始张力来研究导线张力对阻尼器减振效果的影响。本文导线张力选择0.3倍/0.4倍导线拉断力来进行试验研究。图8为不同导线初始张力下，所测得的系统等效阻尼比随阻尼器阻尼系数的变化结果。

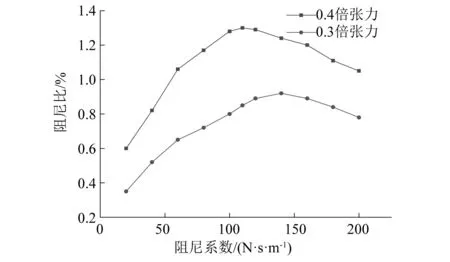
图8 不同初始张力下的系统一阶阻尼比Fig.8 First order damping ratio of system under different initial tension

从图8可知，在不同的导线初始张力下，由于阻尼器的存在，导线-阻尼器系统都会存在一个最大的阻尼比ξmax使阻尼器的减振效果达到最好，且导线张力越大，系统所能达到的最大等效阻尼比ξmax也会越大，但最大阻尼比ξmax所对应的最优阻尼系数Copt则呈现相反的趋势。

3 防舞效果验证

3.1 起舞风速研究

由第2章的室内大比例模型自振试验可知，通过在靠近固定端的位置设置电涡流阻尼器耗散振动能量，能有效提高线路系统的等效阻尼比，从而增加导线系统的防舞能力，为了验证本文提出的防舞装置形式的真实抑舞效果，本节对上述线路安装阻尼器前、后的舞动稳定性进行研究，由李雅普诺夫第一稳定定理可知，导线系统线性化运动方程的特征值实部Re的正负值可以反映非线性系统的稳定性[14]，即Re为正时，导线系统会发生舞动现象。导线系统在风荷载作用下的运动方程可以表示为

(7)

式中：M,Cs,Ks分别为系统的质量、结构阻尼、结构刚度矩阵；Fair为风荷载向量；U为导线系统的位移向量，U=[x,y,z,θ]T；x,y,z,θ分别为导线轴向、竖向、水平向、扭转向位移。

对风荷载向量Fair在U=0处进行泰勒级数展开，忽略位移和速度2次以上项，获得气动荷载的线性化部分

(8)

式中，Cair,Kair分别为系统的气动阻尼、气动刚度矩阵。

将式(8)代入式(7),化简可以得到

(9)

为了便于计算运动方程特征值，计算式(9)的Jacobin矩阵，Jacobin矩阵与线性化运动方程具有相同的特征值[15]。式(9)的Jacobin矩阵可以按式(10)计算

J=

(10)

式中：0为零矩阵，其所有元素均为0；I为单位对角矩阵；λ与P分别为矩阵M的特征值与对应的特征向量。

本节选择对原型线路在易舞风攻角(75°和170°)不同风速下的系统舞动方程的特征值实部进行计算，对比安装阻尼器前、后导线系统竖向舞动的起舞风速以及舞动风速区间变化，并以此来评价该装置的实际抑舞效果。阻尼器安装在靠近固定端L/10.0的位置，阻尼器的刚度、阻尼系数按图6的试验结果选取该位置处的最优参数组合，按动力相似关系换算到原型线路，得到阻尼器的参数为K=0,C=6 508，导线的气动力数据参考杨晓辉等的研究。图9给出在离固定端L/10.0的位置安装阻尼器前后系统运动方程的一阶竖向舞动特征值实部的计算结果。

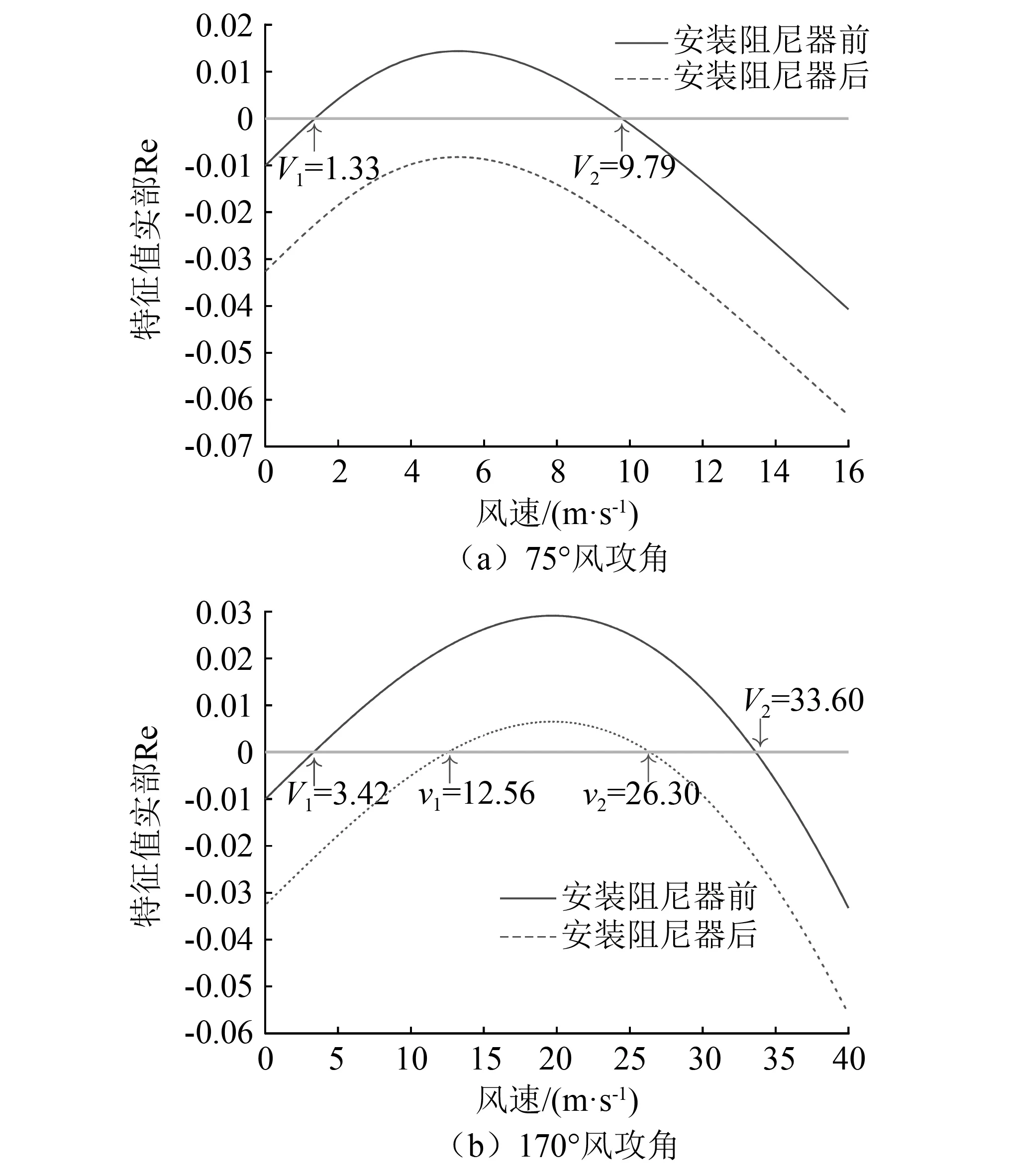
图9 系统线性化运动方程的特征值实部Fig.9 Real part of eigenvalue of linearized motion equation

由图9可知，原始线路在75°和170°下易发生竖向舞动，且起舞风速非常低。由图9(a)可知，在75°风攻角下，安装阻尼器前导线的舞动风速区间为1.33～9.79 m/s, 安装阻尼器后导线系统的等效阻尼比大幅提高，导线不易在该风攻角下发生舞动；由图9(b)可知，在170°风攻角下，安装阻尼器前导线的舞动风速区间为3.42～33.60 m/s, 安装阻尼器后系统的特征值实部大幅减小，导线起舞风速大幅度提高，起舞风速提高到12.56 m/s，且舞动风速区间较原始线路有所缩小，舞动风速区间缩小为12.56～26.30 m/s。由试验结果的分析可知，在线路端部安装阻尼器后，导线系统的等效阻尼比将大幅度提高，在承受相同外部风荷载作用下，系统的总阻尼比也会相应增大，在某些风速下，导线总阻尼比会由负变正，导线不易发生舞动，进而提高了导线起舞风速，缩小了导线舞动风速区间。

3.2 数值模拟研究

为了进一步研究在近端部安装阻尼器的防舞效果，本文利用ANSYS有限元软件研究了原型线路(覆冰八分裂线路)端部设置阻尼器前、后的舞动时程。导线单元采用BEAM188进行模拟，间隔棒采用BEAM188单元模拟，共布置5组间隔棒，两端支座各留27.6 m后跨中等间距每隔55.2 m设置一组间隔棒，两端固定支座高差为0，利用Endrelease命令对每个子导线单元释放BEAM188单元的弯曲自由度，以保证六自由度的间隔棒单元与四自由度的子导线单元在ANSYS软件中可以自动实现自由度缩聚，进而耦合导线4个运动方向的状态，导线的物理参数参考表1。由于COMBIN14单元可以模拟线性阻尼单元与刚度单元并联的情况，阻尼器采用COMBIN14单元进行模拟。覆冰八分裂导线的气动力载荷不仅随时间变化，而且还取决于导体的运动状态，在 ANSYS 中可以获得各子导线的运动状态后，通过编译APDL语言，随着导线运动状态变化的气动力可以定义并应用到有限元模型中，任意时间步长内导体单元的气动力载荷可以基于准稳态模型进行施加，并随后续导线的运动状态改变进行迭代加载，导线的气动力数据参考杨晓辉等的研究。

本文选择对该线路的75°易舞风功角进行数值模拟，阻尼器刚度系数、阻尼系数具体参数选取如表5所示，表5中阻尼系数9 100为刚度K=4 736 N/m下自振试验所确定的最优阻尼系数。图10绘出了75°风攻角9 m/s风速下导线安装阻尼器前、后的跨中舞动时程结果以及阻尼器对导线的作用力。由图10(a)可以看出，原始线路在75°风攻角9 m/s风速下工况下，易激发竖向舞动，最大振幅可以达到1.2 m左右，两侧对称安装阻尼器后，由于阻尼器发挥减振耗能作用，导线系统的等效阻尼比大幅度提高，导线在风荷载作用下的振幅大幅度减小，舞动被有效抑制，基本不发生舞动；且由图10(b)发现，阻尼器对导线的作用力也保持在合理的水平，并随时间呈现下降的趋势，相对于相地间隔棒，优点在于导线和防舞装置连接处的内力较小，对输电导线和输电塔的影响较小。在实际工程应用中，可以考虑在导线与间隔棒线夹处布置缓冲材料(比如橡胶)来进一步减少对导线的磨损。

表5 阻尼器设计参数Tab.5 Design parameters of viscoelastic damper

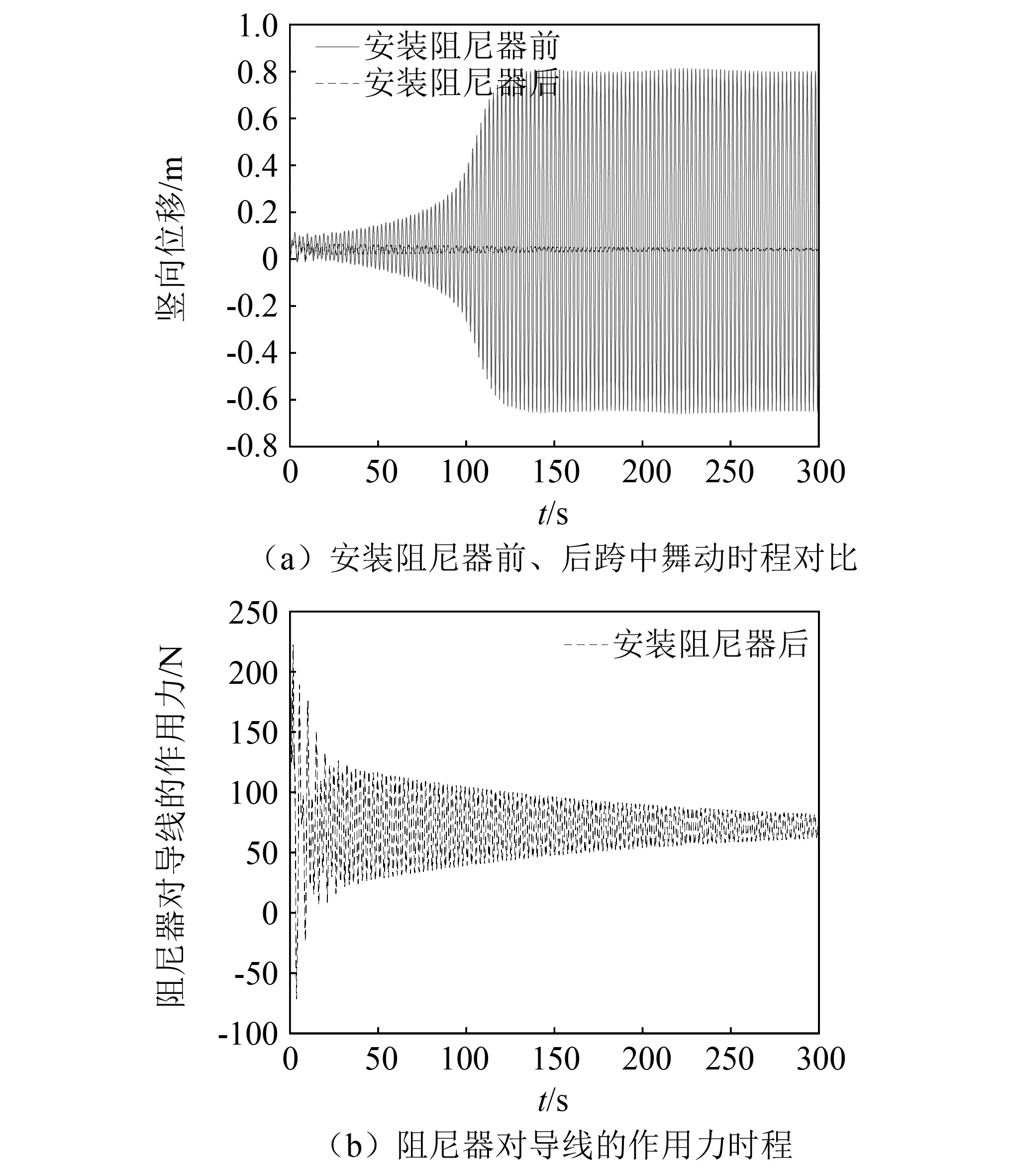
图10 75°风攻角9 m/s风速下安装阻尼器前后舞动仿真模拟结果Fig.10 Galloping simulation results before and after installing dampers under 75° wind attack angle and 9 m/s wind speed

4 结 论

本文设计了导线-电涡流阻尼器系统的大比例缩尺试验模型，并通过自振试验研究了阻尼器的安装位置、刚度、阻尼、导线初始张力等参数对系统的等效阻尼比的影响。通过系统线性化运动方程对导线安装阻尼器前、后的稳定性进行了研究，计算对比了舞动方程的特征值实部。通过ANSYS有限元软件进行仿真模拟，在易舞风攻角下对导线安装阻尼器前、后的舞动位移计算结果进行对比验证，并得到如下结论：

(1) 在靠近输电塔的位置设置阻尼器能大幅度地提高系统的等效阻尼比，阻尼器的安装位置对其提高系统的等效阻尼比影响较大，阻尼器越靠近跨中，效果越突出。在实际工程应用中，为了阻尼器安装拆卸方便以及避免占用导线下部空间，阻尼器安装时可以优先考虑与输电塔塔臂的可靠连接，考虑到电气绝缘要求以及线路安全，阻尼器的安装位置不能过于靠近跨中，本文保守建议此种形式布置下阻尼器安装位置一般不大于L/10.0。

(2) 合理的阻尼器参数对于线路抑舞减振非常重要，在同一刚度下，随着阻尼器阻尼系数的增大，导线系统的结构阻尼比呈现先增大后减小的趋势，存在一个最优阻尼系数Copt使系统阻尼比达到最大ξmax；而阻尼器刚度的存在对于阻尼器发挥减振效果是不利的。

(3) 导线的初始张力也会对阻尼器的减振效果产生影响，导线的初始张力越大系统所能达到的最大阻尼比ξmax会变大，达到最大阻尼比时的阻尼器阻尼系数Copt则会更小。

(4) 由舞动方程的特征值实部计算结果发现，近塔端安装阻尼器能有效提高线路起舞风速，缩小舞动风速区间。

(5) 由ANSYS有限元软件的仿真模拟结果发现，在靠近输电塔的位置设置阻尼器，导线舞动能被有效抑制，验证了该防舞装置良好的防舞性能。