非均匀速度分布对地铁曲线区段钢轨磨耗演变的影响
高 雅, 时 瑾, 焦彬洋, 杨 飞
(1. 北京交通大学 土木建筑工程学院,北京 100044; 2. 中铁物总运维科技有限公司,北京 100036;3. 中国铁道科学研究院集团有限公司 基础设施检测研究所,北京 100081)
钢轨磨耗是铁路运输中的常见现象[1]。地铁系统车辆加减速频繁,行车密度大,且曲线线路较多,钢轨磨耗现象较为突出[2]。地铁曲线区段内外轨不对称磨耗造成轮轨匹配不良,恶化轮轨接触关系,影响运行舒适性和安全性[3-4],增加运营维护成本。
目前国内外学者对轮轨磨耗问题开展了大量研究。Fries等[5]结合Kalker线性蠕滑理论和磨耗理论预测了直线上车轮型面和钢轨轨头的磨耗。Pearce等[6]认为材料的磨耗损失与接触区域的能量消耗成比例,通过车轮每公里产生的磨耗面积来定义为车轮磨耗。Ward等[7]将材料的磨耗量与牵引力和轮轨相对滑动距离联系起来,分别对直线和曲线上车轮型面磨耗进行了预测分析。Braghin等[8]开展了单轮对全尺寸滚动试验台轮轨磨耗试验研究,分析了车轮型面演变。Enblom等[9]分析了轮轨相对滑动、车辆制动及环境对轮轨磨耗的影响。王璞等[10]基于Specht磨耗理论对钢轨型面进行磨耗计算,对不同车型和速度设置权重因子,对重载铁路钢轨磨耗发展规律进行了研究。孙宇等[11]基于Braghin磨耗理论的钢轨磨耗预测模型计算了钢轨磨耗沿纵向和横向的三维分布。王少锋等[12]基于Archard磨耗理论研究了地铁小半径曲线外轨侧磨发展规律。
可以看出,目前对钢轨型面磨耗演化问题的关注较少,针对速度不均匀性对钢轨磨耗影响机理缺乏研究。本文建立一种可计算三维分布的钢轨磨耗预测模型,考虑车辆以非单一速度通过,并设置相应的权重进行磨耗累积计算。同时考虑了车辆通过曲线时内外轨上轮轨接触区域不同的特点,分析了非均匀速度分布对钢轨型面磨耗影响规律,以期对地铁曲线养护维修提供参考。
1 钢轨磨耗计算模型
1.1 钢轨磨耗计算主要流程
研究钢轨磨耗的发展规律,需要了解轮轨之间的相互作用关系,根据计算得到的轮轨动力学响应分析轮轨滚动接触情况,再结合磨耗理论计算轮轨接触区域内的钢轨磨耗分布,当钢轨磨耗达到一定深度时要采用平滑方法对钢轨型面进行平滑更新,利用更新后的钢轨型面重复上述过程进行钢轨磨耗计算,得到新的更新后钢轨型面,由此反复迭代计算直到满足终止条件。在每一次钢轨磨耗计算中,不同工况条件下得到的钢轨断面磨耗分布可以通过一定方式进行叠加获得总体磨耗情况。
钢轨磨耗计算模型由车轨动力学仿真、轮轨滚动接触计算,钢轨型面磨耗计算以及钢轨型面更新几个部分组成,如图1所示。
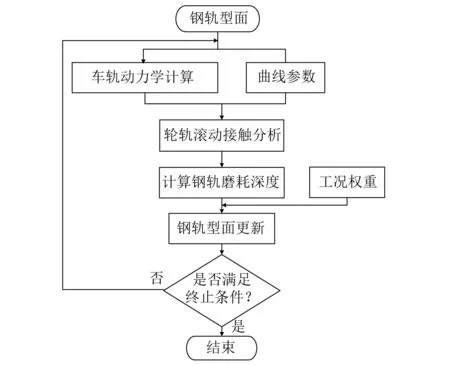
图1 钢轨磨耗计算流程图Fig.1 Flow chart of rail wear calculation
1.2 车辆与轨道动力相互作用模型
本文建立的曲线区段车辆与轨道动力相互作用模型,如图2所示。将车辆简化为多刚体系统,一系、二系悬挂系统简化为弹簧、阻尼元件,共考虑35个自由度。轨道结构选用地铁系统中常见的钢弹簧浮置板减振轨道模型,考虑钢轨和轨道板的振动。其中钢轨简化为离散弹性点支承基础上的连续欧拉梁,考虑其横向、垂向和扭转振动。轨道板在垂向简化为弹性矩形薄板,横向和转动方向简化为刚体,扣件和钢弹簧均简化为弹簧、阻尼系统。轮轨法向力、蠕滑力分别采用Hertz线性接触理论和沈志云-Hedrick-Elkins理论进行求解,车轨系统方程采用新型两步数值积分方法[13]进行求解。关于车辆与轨道动力相互作用模型的详细描述可见文献[14]。

图2 车辆与轨道动力相互作用模型Fig.2 Vehicle and track dynamic interaction model
1.3 轮轨非Hertz滚动接触模型
基于车辆与轨道动力相互作用计算,根据车轨系统动力学参量进一步研究接触斑上的轮轨滚动接触问题。在钢轨的磨耗分析中,采用基于虚拟渗透的非Hertz接触理论[15]求解轮轨间的滚动接触,该方法是近年来轮轨滚动接触计算中广泛应用的一种方法。考虑到轮轨的几何外形,接触斑通常是非椭圆的。假设接触斑形状可以由轮轨型面和相对压入量直接决定,使得虚拟渗透区域变得足够接近真实接触区域。定义轮轨之间恰好接触且无接触压力和弹性变形时,轮轨之间的接触点为几何接触点,如图3所示。基于弹性半空间理论,轮轨间的相对压入量满足
(1)
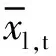
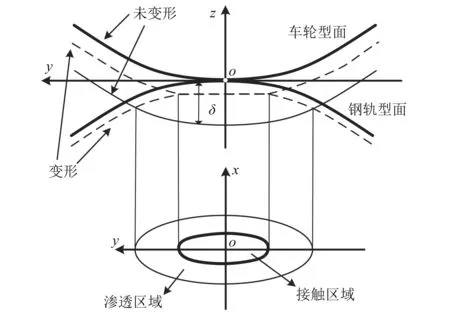
图3 虚拟渗透区域和接触区域Fig.3 The virtual region area and contact region
根据虚拟渗透量δ确定轮轨型面之间的虚拟渗透区域,将此虚拟渗透区域视为接触区域。由于车轮是一个旋转体,因此假定考虑的接触具有Hertz接触的某些性质。根据Hertz理论,假设法向压力沿滚动方向呈半椭圆分布,则接触斑上的压力分布具有以下形式
(2)
式中,p0为最大接触压力。通过对接触压力进行积分可以得到法向接触力为
(3)
为了计算最大接触压力并保证该方法的可靠性,只在接触区域的一个点,即几何接触点(0,0)处满足Boussinessq-Cerruti公式。切向接触计算是根据每个接触斑的等效接触椭圆计算该接触斑的Kalker线性系数,再根据FASTSIM算法求解切向力分布,从而判断接触斑上的黏着、滑动区分布。通过这种方法求解轮轨滚动接触问题,是完全可靠并且快速的。
1.4 磨耗模型
钢轨磨耗计算采用Archard磨耗模型[16],该磨耗模型认为材料的磨耗损失量与接触法向压力、相对滑动距离成正比,与接触物体材料硬度成反比,即
(4)
式中:Vw为材料磨耗体积;S为接触物体相对滑动距离;H为接触物体材料硬度;N为法向接触力;K为磨耗系数。
将可能的接触区域进行单元划分,如图4所示。假设每个单元的接触压力均为定值,并通过单元中心点的受力表征整个单元受力。对于接触斑上的任意单元J,其法向力可以表示为PJ=pJΔxΔy,车轮通过后单元J上的磨耗体积可以表示为VwJ=(ΔxΔy)VdJ。根据上式,则单元J中心处的磨耗深度VdJ可以表达为
(5)
式中:pJ为单元J上的法向接触压力;SJ为单元J上的滑动距离, 一般可以表达为
(6)
(7)
式中:KJ为单元J的磨耗系数;v为列车运行速度; Δx和Δy分别为单元沿车轮滚动方向和沿钢轨横断面方向上的长度(本文采用单元面积为0.1 mm×0.1 mm);vslipJ单元J上的滑动速度;ζ1,ζ2和ζ3分别为纵向、横向和扭转蠕滑系数;uJ为弹性位移;xJ,yJ分别为单元J中心点在x,y方向上的坐标。

图4 轮轨接触斑Fig.4 The wheel-rail contact patch
1.5 非均匀速度分布模型
为了研究非均匀速度分布对钢轨磨耗发展规律的影响,采用了三角概率密度分布[17]模拟车辆通过速度分布情况。定义了两种约束条件:期望值与标准差恒定及期望值与域宽恒定。图5给出了速度的一般三角形偏态概率分布。对于速度概率分布函数p(v),可以表达为关于车辆运行速度上下限vmin,vmax及众数vm的表达式,即
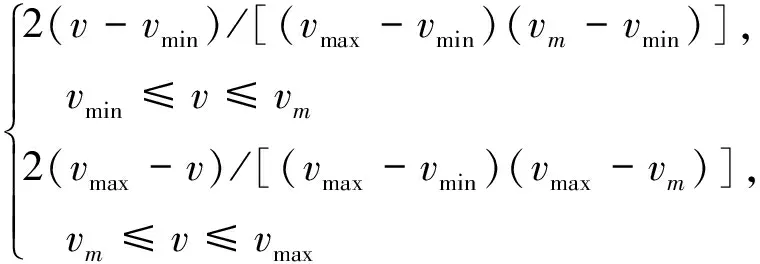
(8)

(9)

(10)
vw=vmax-vmin
(11)
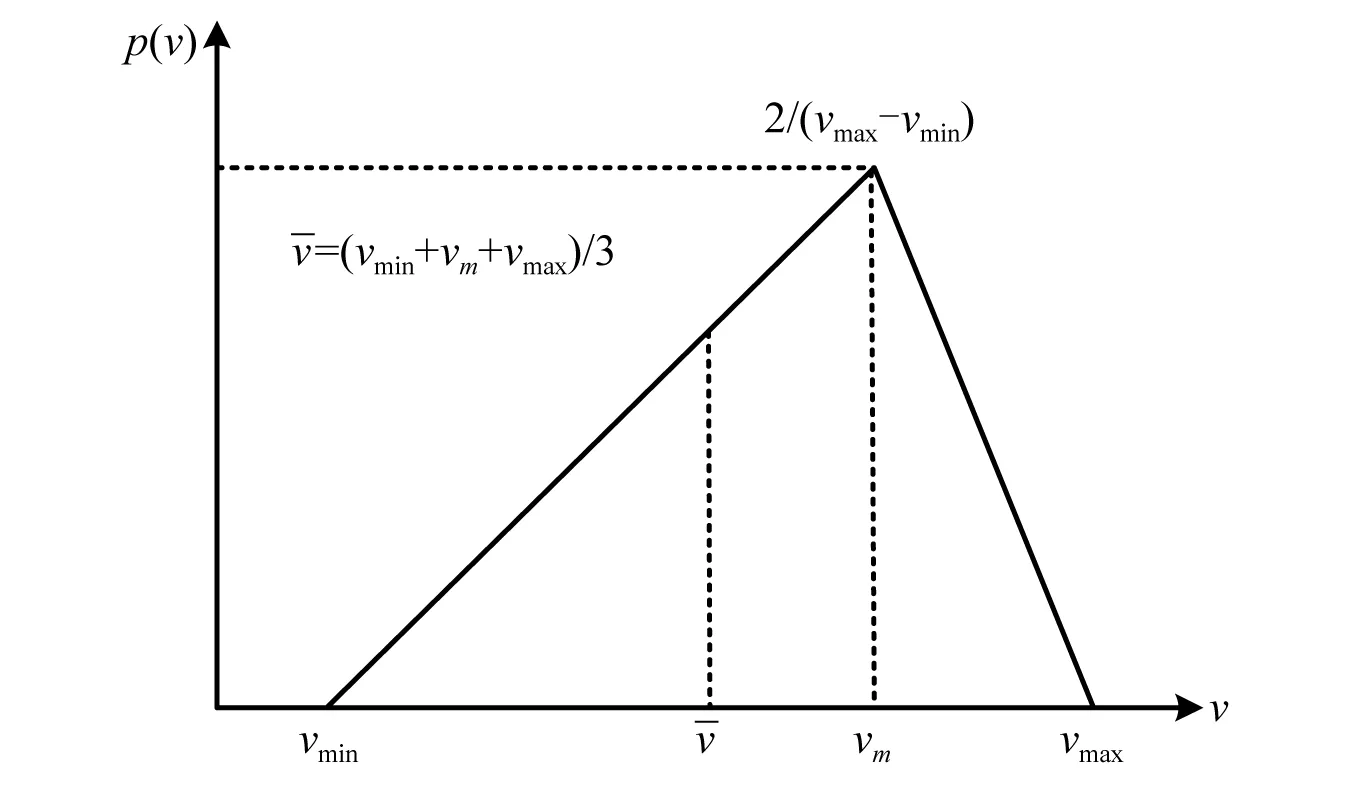
图5 速度分布概率密度函数Fig.5 Probability density function of speed distribution
偏度是概率分布密度函数相对于其期望值不对称程度的标准度量,对于非均匀速度分布模型,偏度可以定义为分布速度关于速度期望值的三阶标准化距,其定义式为
(12)
1.6 钢轨型面更新策略
在钢轨磨耗计算中,车轮通过某钢轨断面时,通过接触斑上沿车轮滚动方向磨耗分布叠加表征该断面的磨耗。在轨道上沿纵向采用等间距采样,考虑4位轮对,则某辆车通过第m个钢轨截面时的钢轨磨耗可以写为该车所有车轮通过该截面钢轨磨耗的和,即
(13)
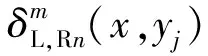
不同钢轨断面上的轮轨相互作用动力学响应不同,导致钢轨磨耗情况沿轨道纵向发生变化。但是在两相邻钢轨断面间距较小时,磨耗情况相差不大。考虑到计算效率,本文按照固定间隔计算钢轨磨耗,磨耗计算断面之间的钢轨磨耗可以通过插值获得。本文中两个相邻钢轨计算断面之间间距为1 m,如图6所示。
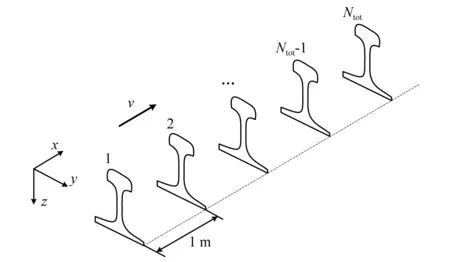
图6 磨耗计算钢轨断面分布Fig.6 Rail cross section distribution of wear calculation
考虑到非均匀速度分布对钢轨磨耗发展的影响,将k个通过速度定义为k个运行工况,对不同工况下计算得到的钢轨磨耗进行线性叠加,则考虑非均匀速度分布后第m个钢轨断面上的平均磨耗深度可以表示为
(14)
式中,ps为第s个工况所占权重。
对于产生磨耗的钢轨型面,规定当钢轨的磨耗深度达到限值后对钢轨型面进行更新,采用更新后的钢轨型面进行下一次磨耗计算。本文中定义钢轨型面上的计算磨耗深度达到0.1 mm时需要对钢轨型面进行更新,更新时采用均匀B-spline函数对钢轨型面进行平滑。
假设钢轨型面更新前形状不发生变化,则每辆车通过某一钢轨断面时的钢轨磨耗是不变的。由此第q次更新时的钢轨型面总磨耗量可以表达为
(15)
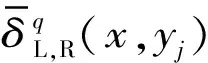
(16)
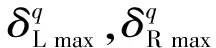
2 工况分析
2.1 基本概况
本文选取一段地铁曲线线路进行仿真计算。线路曲线半径650 m、超高120 mm;曲线段和缓和曲线段的长度分别为482 m和85 m。轨道类型采用钢弹簧浮置板,扣件间距为0.6 m,钢弹簧支撑间距为扣件间距的两倍。图7给出了仿真计算选用的轮轨型面,车轮型面为实测磨耗车轮型面,钢轨型面为实测磨耗钢轨型面和优化钢轨型面,轨道不平顺选用地铁实测轨道随机不平顺,垂向叠加轨道短波不平顺,详见Shi等的研究。其中: “worn”代表磨耗钢轨型面; “opt”代表优化钢轨型面。考虑车辆以单一速度93 km/h和速度期望值为93 km/h,标准差系数为15%,偏度S为0的非均匀速度分布通过时的钢轨磨耗情况,迭代更新次数为10次。图8给出了非均匀速度分布通过时的速度概率分布函数曲线。

图7 轮轨型面Fig.7 Wheel-rail profile
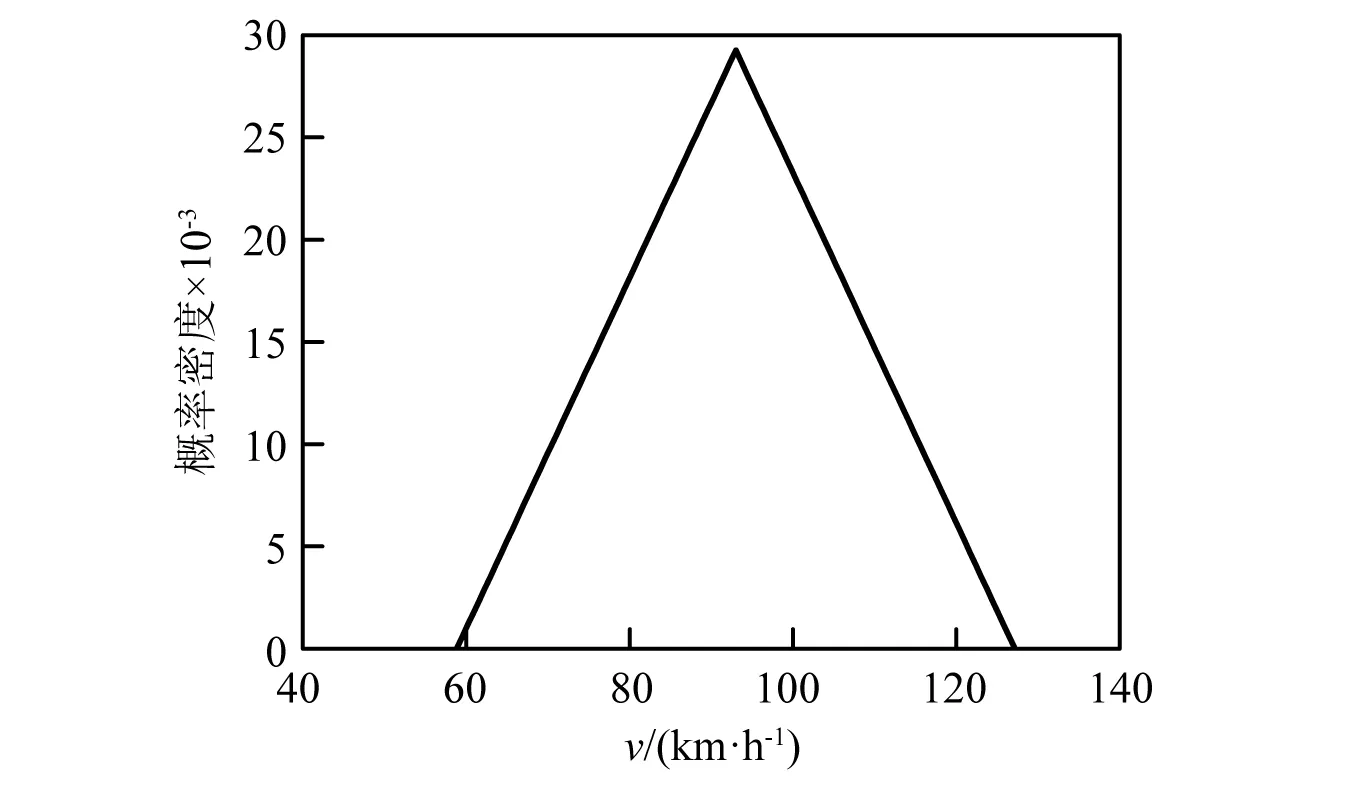
图8 速度概率密度分布图像Fig.8 Speed probability density distribution image
2.2 计算结果
2.2.1 钢轨磨耗深度分布特性
为了充分了解非均匀速度分布对地铁曲线区段钢轨磨耗的影响,图9~图16分别给出了单一速度通过和非均匀速度通过时,磨耗钢轨型面和优化钢轨型面第1次和第10次更新时磨耗深度分布。图中横轴表示沿轨道纵向方向,纵轴表示钢轨横向,颜色变化显示了钢轨磨耗深度变化情况。其中纵轴为负表示内外轨轨头内侧。由图可知,内外轨在圆曲线上的磨耗明显大于曲线其他位置,钢轨的磨耗区域基本平行于横轴,计算得到的钢轨光带基本是平直的,但磨耗深度沿轨道纵向分布是不均匀的,初始曲线段磨耗钢轨型面外轨最大磨耗深度大于内轨,优化钢轨型面外轨最大磨耗深度小于内轨。
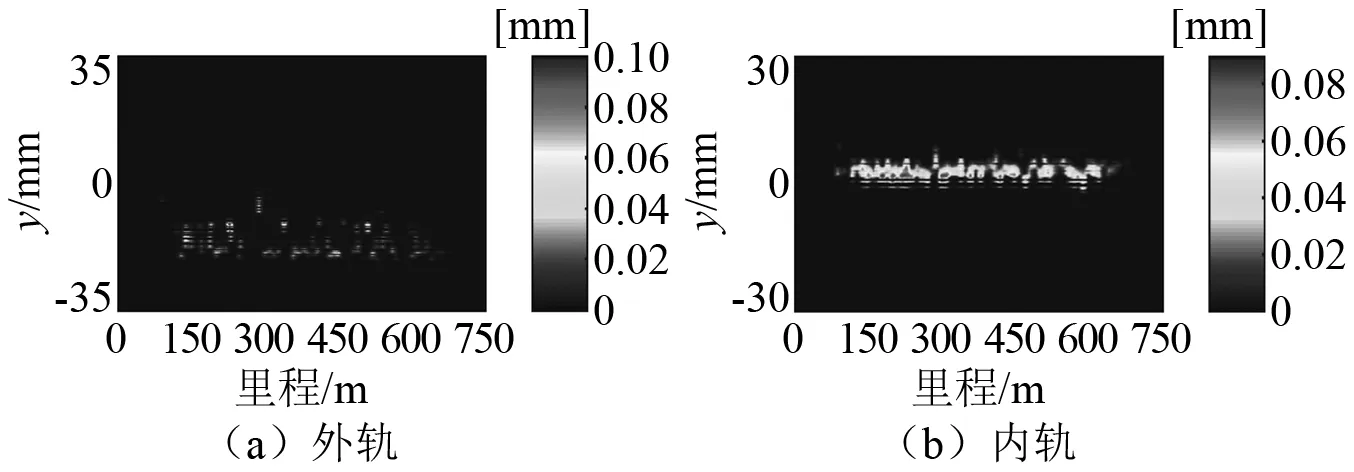
图9 单一速度通过时第1次更新时磨耗钢轨型面磨耗深度分布Fig.9 Wear depth distribution of worn rail profile after the 1st update with single speed

图10 单一速度通过时第1次更新时优化钢轨型面磨耗深度分布Fig.10 Wear depth distribution of optimized rail profile after the 1st update with single speed

图11 单一速度通过时第10次更新时磨耗钢轨型面磨耗深度分布Fig.11 Wear depth distribution of worn rail profile after the 10th update with single speed

图12 单一速度通过时第10次更新时优化钢轨型面磨耗深度分布Fig.12 Wear depth distribution of optimized rail profile after the 10th update with single speed
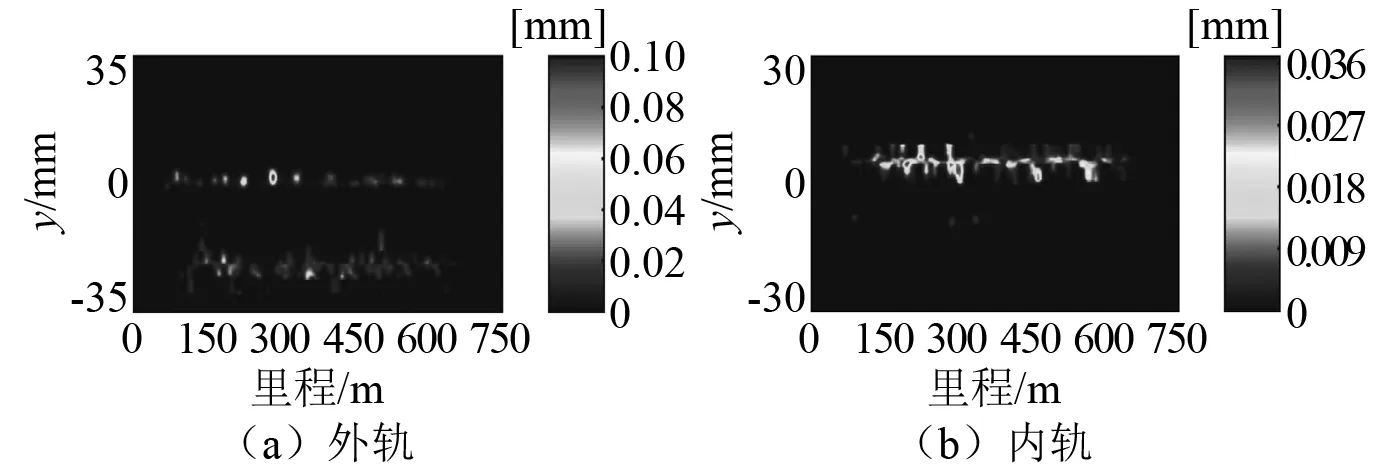
图15 非均匀速度通过时第10次更新时磨耗钢轨型面磨耗深度分布Fig.15 Wear depth distribution of worn rail profile after the 10th update with non-uniform speed

图16 非均匀速度通过时第10次更新时优化钢轨型面磨耗深度分布Fig.16 Wear depth distribution of optimized rail profile after the 10th update with non-uniform speed
通过第1次和第10次更新时钢轨磨耗深度分布对比可以看出,单一速度通过时,磨耗钢轨型面的磨耗光带位置基本没有发生变化,磨耗区域的范围略有增加,优化钢轨型面局部磨耗较大,整体磨耗明显小于磨耗钢轨型面;磨耗钢轨型面内轨磨耗区域靠近钢轨中心的轨头外侧,优化钢轨型面内轨磨耗区域分布在钢轨中心附近。非均匀速度通过时,磨耗钢轨型面和优化钢轨型面内轨磨耗区域均大于单一速度通过;随着钢轨型面更新次数的增加,钢轨最大磨耗深度逐渐增加,磨耗钢轨型面内轨磨耗区域由钢轨中心向两侧移动,磨耗光带宽度明显增加。相较于单一速度通过时的钢轨磨耗深度分布,经过10次更新后非均匀速度通过的钢轨磨耗深度分布沿轨道纵向更均匀,不同钢轨断面的磨耗差异明显减小,磨耗钢轨型面和优化钢轨型面内轨磨耗光带宽度均为10 mm左右,但磨耗钢轨型面外轨侧磨严重。
随着钢轨型面更新次数的增加,钢轨的磨耗速率逐渐变化,图17给出单一速度和非均匀速度通过时磨耗钢轨型面和优化钢轨型面更新时累计通过车辆数量统计图。由图可知,随着钢轨型面更新次数的增加,累计通过车辆数量的增加速率先减小后增加,说明钢轨磨耗速率先增加后减小。优化钢轨型面更新时的通过车辆数量明显大于磨耗钢轨型面,且随着更新次数的增加优化钢轨型面与磨耗钢轨型面累计通过车辆数量差值逐渐增加,采用优化钢轨型面在第10次更新时以单一速度通过和非均匀速度通过时的累计通过车辆数量相较于磨耗钢轨型面分别增加了61%和49%。同时,车辆以非均匀速度通过时的累计通过车辆数量显著大于单一速度通过时的情况。第10次更新时,相较于单一速度通过,以非均匀速度通过时磨耗钢轨型面的累计通过车辆数量增加了16%,优化钢轨型面增加了8%。第10次更新时采用非均匀速度通过和优化钢轨型面与采用单一速度通过和磨耗钢轨型面相比,车辆累计通过数量增加了近一倍,显著减小了钢轨磨耗速率。

图17 累计通过车辆数量Fig.17 Cumulative number of vehicles passing
2.2.2 钢轨磨耗对轮轨接触几何的影响
随着更新次数的增加,钢轨型面逐渐发生变化,轮轨匹配时接触点位置相应也发生变化。图18~图21给出了10次更新后,单一速度和非均匀速度通过时磨耗钢轨型面和优化钢轨型面与磨耗车轮型面匹配的接触点分布图像,其中轮对横移量为0~20 mm。由图可知,磨耗钢轨型面内轨在单一速度通过10次更新后轨顶出现明显凹磨,轮轨接触点向钢轨中心轨头内侧移动,外轨接触点分布较为分散;非均匀速度通过10次更新后轮轨接触点分布不连续。优化钢轨型面在10次更新后轮轨接触点分布连续性较好;与单一速度通过相比,非均匀速度通过轮轨静态接触点分布区域范围较大,且接触点分布更均匀。
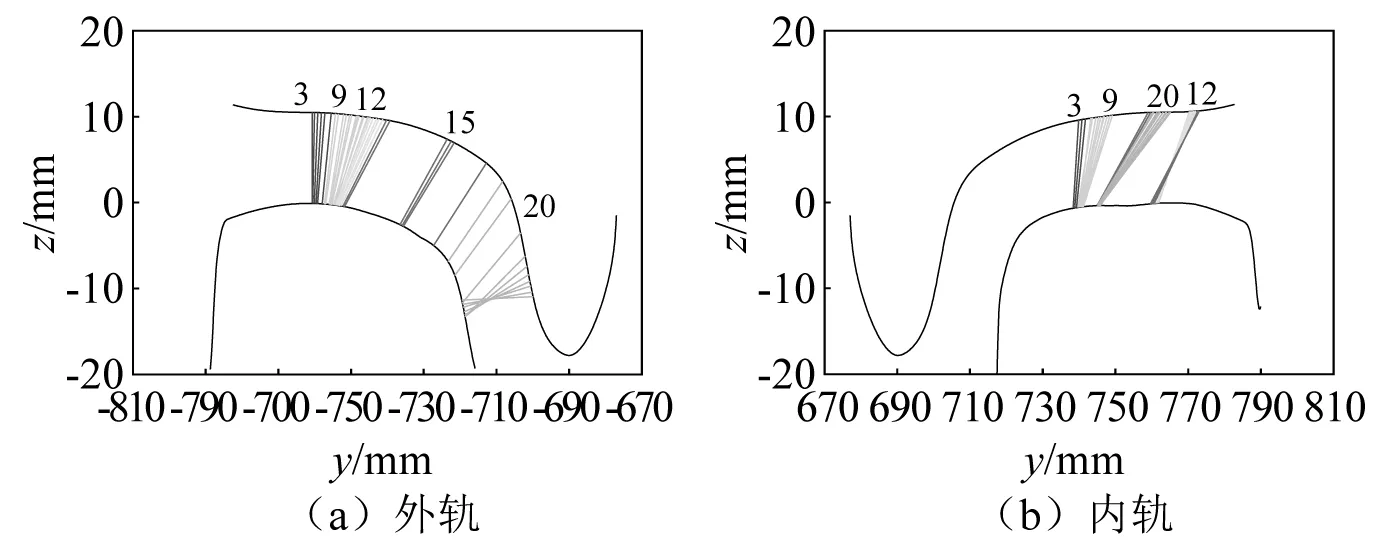
图18 单一速度通过时第10次更新后磨耗钢轨型面与磨耗车轮型面接触点分布Fig.18 Distribution of contact points between worn rail profile and worn wheel profile after the 10th update with single speed

图19 单一速度通过时第10次更新后优化钢轨型面与磨耗车轮型面接触点分布Fig.19 Distribution of contact points between optimized rail profile and worn wheel profile after the 10th update with single speed
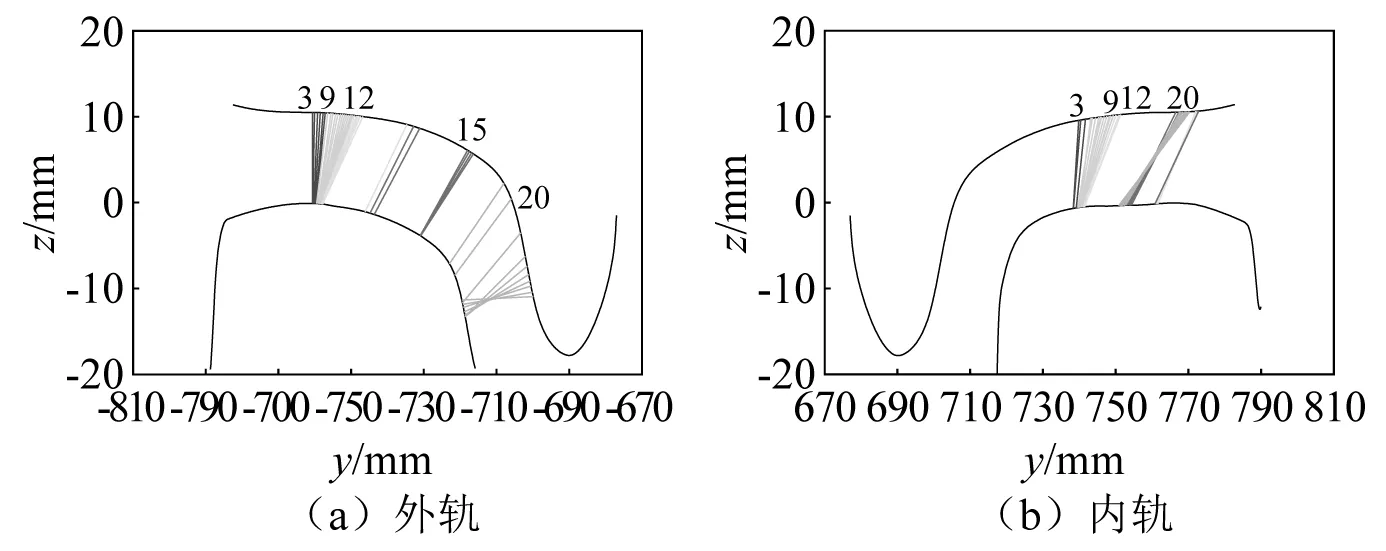
图20 非均匀速度通过时第10次更新后磨耗钢轨型面与磨耗车轮型面接触点分布Fig.20 Distribution of contact points between worn rail profile and worn wheel profile after the 10th update with non-uniform speed
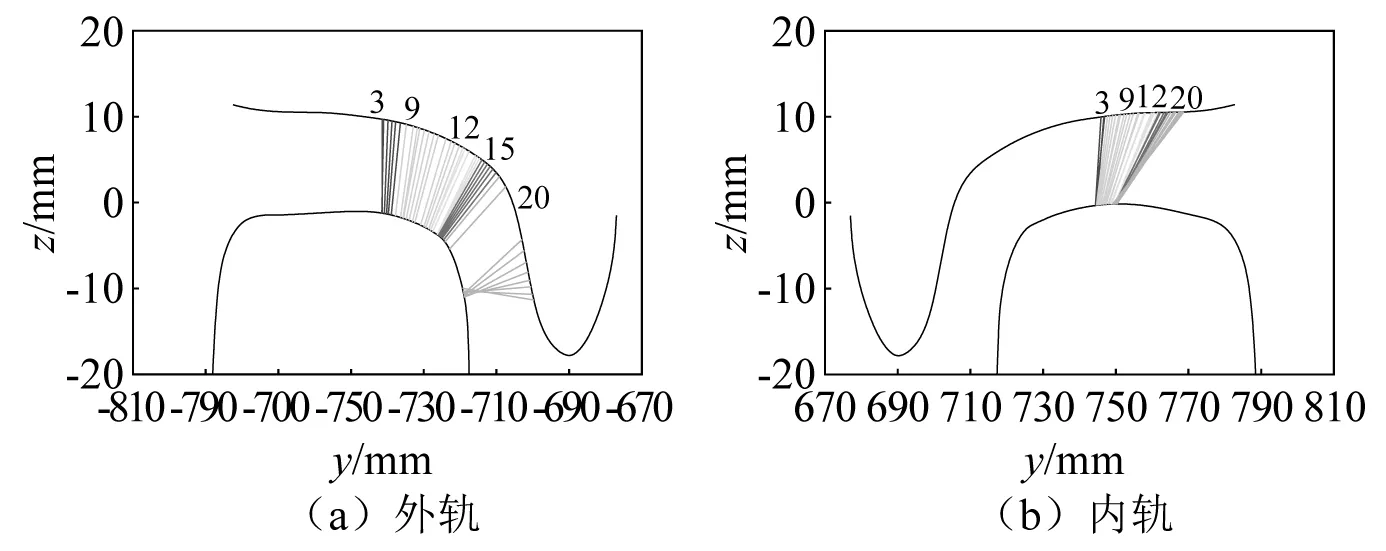
图21 非均匀速度通过时第10次更新后优化钢轨型面与磨耗车轮型面接触点分布Fig.21 Distribution of contact points between optimized rail profile and worn wheel profile after the 10th update with non-uniform speed
图22和图23给出了钢轨型面10次更新后滚动圆半径差和等效锥度随轮对横移量变化情况。由图可知,优化钢轨型面的滚动圆半径差和等效锥度明显大于磨耗钢轨型面,采用优化钢轨型面的轮对恢复对中能力更好,曲线通过能力也更强。同时磨耗钢轨型面滚动圆半径差曲线平顺性较差,尤其是单一速度通过时,说明轮轨接触点分布连续性较差。

图22 钢轨型面第10次更新后滚动圆半径差图像Fig.22 Image of rolling radius difference after the 10th update of rail profile
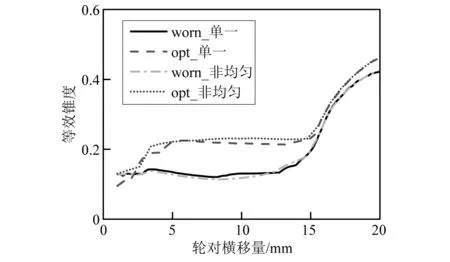
图23 钢轨型面第10次更新后等效锥度图像Fig.23 Image of equivalent conicity after the 10th update of rail profile
由此可见,钢轨型面磨耗会对轮轨接触几何产生明显影响,随着钢轨磨耗深度逐渐增加,轮轨接触点位置逐渐变化导致磨耗范围逐渐变化,钢轨磨耗向为产生磨耗的区域发展,磨耗范围逐渐增加。车辆以单一速度通过曲线时,轮轨接触区域变化较小,钢轨磨耗较为集中,容易造成钢轨型面局部磨耗较大。
2.2.3 钢轨磨耗对行车性能的影响
钢轨型面磨耗导致轮轨接触几何发生变化,直接影响轮轨动态相互作用关系。本节根据车辆以93 km/h的速度在10次更新后的钢轨型面上运行时的行车性能进行分析。图24和图25给出了单一速度和非均匀速度通过时一位轮对脱轨系数和轮重减载率时程响应。通过对比可以看出,单一速度通过曲线时的脱轨系数和轮重减载率均明显大于非均匀速度通过时的情况。与非均匀速度通过相比,单一速度通过时产生的钢轨磨耗容易使轮轨间出现瞬时冲击,轮轨间动力相互作用加剧。图26和图27给出了单一速度和非均匀速度通过时圆曲线中点处钢轨横向加速度和轨道板横向加速度时程响应。由图可知,单一速度通过时圆曲线中点处的钢轨和轨道板中心横向加速度明显大于非均匀速度通过时的情况。非均匀速度分布增加了钢轨磨耗的均匀性,在一定程度上减小了轮轨横向振动幅值。
图24 一位轮对脱轨系数Fig.24 Derailment coefficient of the 1st wheelset

图25 一位轮对轮重减载率Fig.25 Rates of wheel load reduction of the 1st wheelset

图26 圆曲线中点处钢轨横向加速度Fig.26 Lateral acceleration of rail at the middle of curve
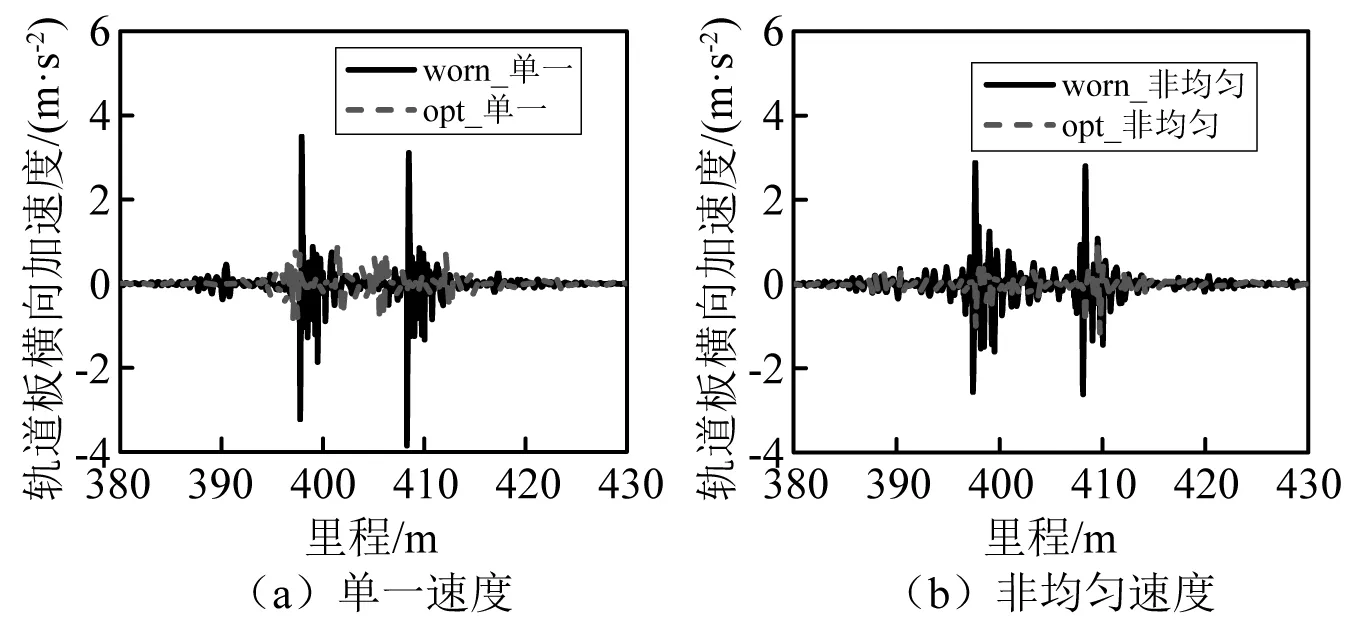
图27 圆曲线中点处轨道板横向加速度Fig.27 Lateral acceleration of track slab at the middle of curve
同时,通过磨耗钢轨型面和优化钢轨型面的动力响应对比也可以看出,采用优化钢轨型面有效改善了车辆通过时的行车性能,车辆运行稳定性显著提高。
3 结 论
(1) 钢轨磨耗光带与轨道纵向基本平行,磨耗深度沿轨道纵向分布不均匀。随着通过车辆数量的增加,钢轨磨耗区域范围逐渐增加,内轨磨耗区域向钢轨轨头内侧移动,钢轨磨耗速率先增加后减小。
(2) 与磨耗钢轨型面相比,采用优化钢轨型面有效降低了曲线外轨侧磨,减缓了钢轨磨耗速率。10次更新后单一速度通过和非均匀速度通过时采用优化钢轨型面的累计通过车辆数量分别增加了61%和49%。同时优化钢轨型面在10次更新后能够保证轮轨匹配良好。
(3) 与单一速度通过相比,采用非均匀速度通过进一步减小了钢轨磨耗速率。与采用单一速度通过和磨耗钢轨型面相比,采用非均匀速度通过和优化钢轨型面10次更新后累计通过车辆数量增加了近一倍。同时采用非均匀速度通过显著提高了钢轨磨耗均匀性,减小了车辆通过曲线时轮轨间异常冲击,车辆运行稳定性好。
(4) 由于地铁车辆是通过ATO来控制运行的,通常情况下地铁车辆通过曲线区段时运行速度是不变的,而地铁车辆以单一速度通过曲线时会造成钢轨磨耗加快,因此在地铁实际运营中可通过在高峰和低峰时段采取非均匀速度控制模式,在一定程度上减缓钢轨磨耗速率。

