综合斜率和三次样条的EMD端点效应抑制方法

梁黎明， 王茂芝， 徐文皙， 谭梦婷， 张明月， 王尚坤

(1. 成都理工大学 数理学院，成都 610059; 2. 成都理工大学 数学地质四川省重点实验室，成都 610059)

自从Huang等[1-2]于1998年提出经验模态分解方法(empirical mode decomposition, EMD)以来，该方法被广泛应用于各学科领域非线性非平稳信号处理。EMD将信号分解为频率由高到低的本征模态函数(intrinsic mode function, IMF)，是一种完全自适应的信号分析方法。然而，EMD在提取IMF时，依据信号局部极值点构建其上、下包络线，而信号端点通常不是极值点，进而需要借助端点延拓才能使包络线覆盖信号并进行后续操作。不良的端点延拓会导致包络线两端的误差放大，进而在所提取的IMF分量中 (特别是在IMF的两端) 出现虚假成分，并且这些虚假成分逐渐向内“传播”，最终造成信号分解结果失真，产生所谓的端点效应。当输入信号较短、频率较小时，端点效应更为明显，进而导致所提取的IMF失去物理意义。因此，抑制和消除端点效应是EMD应用的重要前提，受到学者的广泛关注。

已有研究表明，抑制EMD端点效应的端点延拓算法设计主要从增加信号两端极值点来实现延拓包络线的目的。如：Rilling等[3]提出的镜像法以信号两端的第一个极值点为边界，把信号向外映射，通过获取原信号的镜像得到一个覆盖原信号的包络曲线；王红军等[4]提出改进的多项式拟合法，利用端点处的三个极值点进行多项式拟合，将计算值作为延拓点的近似取值；Huang等[5]提出极值法，以端点的一个特征波为依据，在两端各延拓两个极大值点和极小值点；Datig等[6]提出斜率法；Wu等[7]在Datig等的基础上提出改进的斜率方法(improved slope based method, ISBM)，根据信号端点相邻极值点求得斜率，利用端点的第一个极值点和斜率确定延拓点所在的线性方程，以此确定延拓点的位置；Xu等[8]提出基于三次样条的延拓算法(cubic spline based method, CSBM)，利用延拓后的包络线必须覆盖原包络线的限制，确定信号两端局部极值点与延拓点之间的关系，得到满足条件的延拓点。此外，还有利用Lyapunov指数预测模型[9]和波形特征[10]来预测延拓点，以及采用其他类型的样条函数[11-12]拟合包络线进行延拓。

CSBM由于较好地控制了延拓包络线和原始包络线在共同区域内保持一致的特性，具有良好性能。但同时，CSBM在确定延拓点坐标位置时依靠文中提出的两个准则及包络线来确定，缺乏对信号趋势的考量。另一方面，ISBM在延拓点位置的确定上，利用斜率来刻画信号局部趋势。本文提出一种基于斜率和三次样条相结合的端点延拓方法(slope and cubic spline based method, S-CBM)，该方法综合了ISBM和CSBM的优势，能有效抑制端点效应对EMD分解结果的影响。

1 EMD算法

与傅里叶变换和小波变换等传统方法相比，EMD是一种新型的时间序列分析方法。该方法依据数据自身时间尺度特征进行信号分解，无须预设基函数，克服了传统时频分析方法需要确定基函数的局限性。理论上，EMD可以应用于任何类型的信号处理，特别在处理非平稳非线性数据上具有明显优势。通过EMD筛选出来的IMF需满足两个准则：一是上包络线和下包络线均值为零；二是极值点个数与过零点个数最多相差一个。

任给一个测试信号x(t)，IMF的提取过程如表1所示。

表1 EMD算法Tab.1 EMD algorithm

若筛选过程在n次迭代后停止，测试信号x(t)可以被表示为

式中，r为剩余分量，代表信号的平均趋势。

由于EMD算法中筛选IMF的两个条件过于苛刻，因此常用另一个有效判断工具[13-14]标准偏差(standard deviation, SD)来替代。当SD小于某个指定阈值(本文SD=0.05)时，终止筛选。其定义为

2 基于斜率和三次样条的端点延拓算法

为描述方便，表2给出了有关符号定义和变量说明。

表2 符号定义和变量说明Tab.2 Symbol definition and variable description

由于延拓点的“好坏”将直接决定EMD分解的端点效应程度，如何最大程度利用已有的信息合理确定延拓点位置是解决端点效应的关键。本文的设计思路是：从信号及其包络变化趋势两个角度共同来控制延拓点位置。其中信号变化趋势度量是利用在信号两端相邻局部极值计算两个斜率值，并以斜率变化率作为延拓点所在直线的斜率，进而构造延拓点的直线方程。另一方面，采用CSBM方法确定延拓点需满足的另一个方程。最后通过联立求解两个方程来确定延拓点的坐标位置。这种设计思路同时充分考虑了信号及其包络的变化趋势，进而一定程度也克服了CSBM仅依靠包络线来确定延拓点位置的局限性。

该算法需在信号两端各延拓一个局部极大值点和一个局部极小值点。下面以信号左端延拓点为例，介绍并描述算法，算法示意图如图1所示。右侧延拓点可在此基础上推导得到。

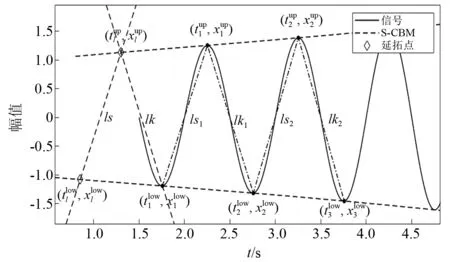
图1 基于S-CBM的信号左端延拓Fig.1 Extension of the signal’s left end of by S-CBM

表3 综合斜率和CSBM的端点延拓方法Tab.3 Algorithm description of end condition method combined slope and CSBM

表3(续)

图1示例了按照表3算法流程得到阻尼正弦信号x(t)=sin(2πt)·e0.1t左端延拓极值点的计算情况(此时第一个极值点是极小值点)。

3 试验结果与性能分析

本文设计了四个模拟信号和两个实际工程应用信号对算法性能进行测试。四个模拟信号简述如下：第一个测试信号采样频率为200 Hz；第二个是由两个调幅信号组成的采样频率为300 Hz的信号；第三个由高、中、低频信号构成，采样频率为400 Hz；第四个例子为一个非平稳信号，采样频率为200 Hz。四个信号的数学表达式定义如下，信号波形如图2所示。两个实际工程应用信号来自美国凯斯西储大学轴承数据中心的一段正常电机驱动端加速度以及风扇端加速度的数据[16]，分别记为x5(t)和x6(t)，如图3所示。

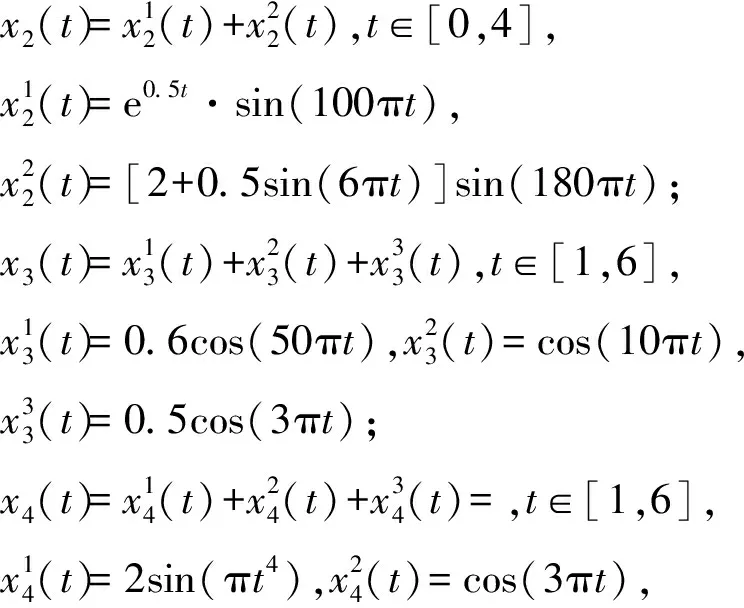
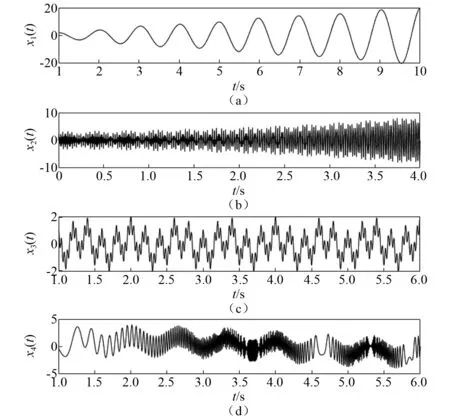
图2 模拟信号Fig.2 Analog signals

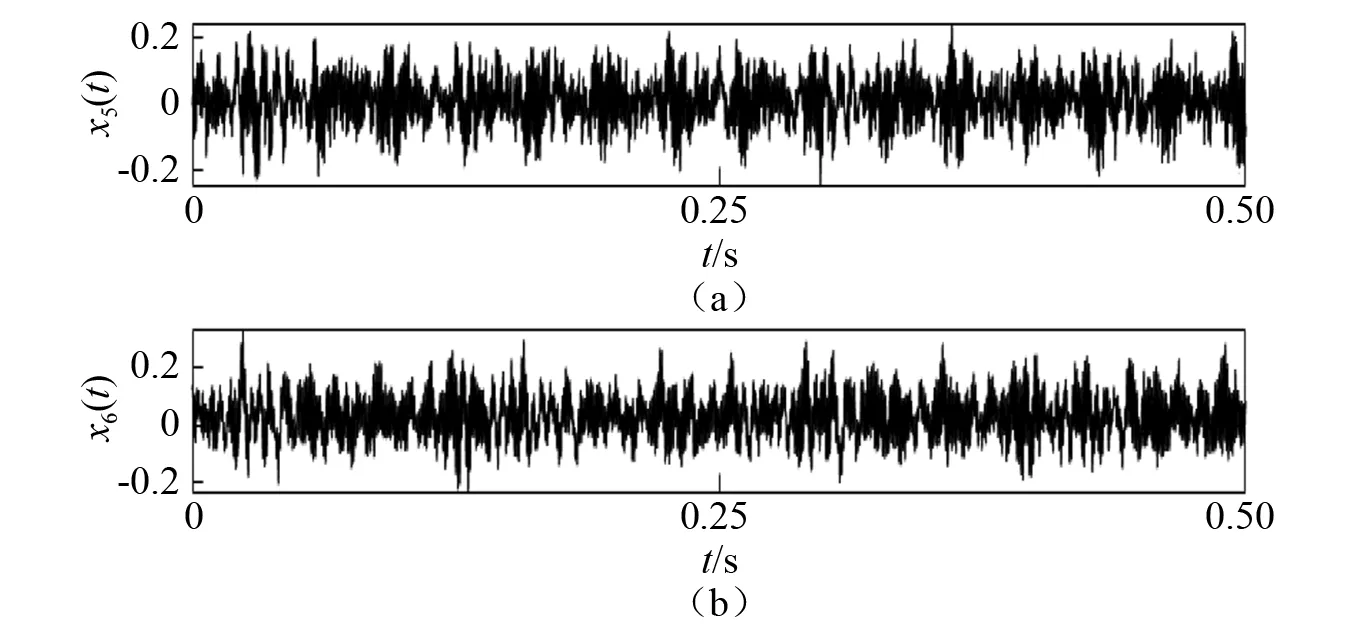
图3 实际工程信号Fig.3 Practical engineering signals

3.1 算法性能度量指标

本文考虑三个度量指标对延拓效果进行评估。

第一个度量指标是由Huang等提出的正交指数(index of orthogonality, IO)，其定义为

式中：x(t)为原始信号；IMFi(t),IMFj(t)分别为原始信号x(t)的第i、第j个IMF分量，IO评估IMFs的正交性。理论上，IO越小，信号分解的效果越好。

第二个度量指标是均方误差(mean squared error, MSE)，该指标对具有确定分量的输入信号进行评估，MSE定义为

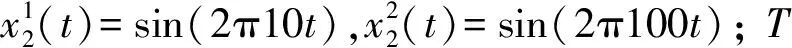
第三个指标定义为能量误差θ。在EMD分解过程中，所有IMF的能量总和应等于原信号的能量，但由于能量泄漏等原因，IMF的能量总和往往无法与原信号保持一致。因此可以通过比较EMD分解前后的能量，评估端点效应的影响程度。能量误差θ可描述为

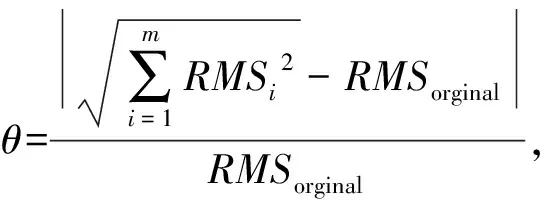
式中：si(t)为原始信号或IMF分量；RMS为信号的有效值；m,n分别为IMF的总个数和样本数；θ值越小，信号分解效果越好。

3.2 试验结果对比

本节仅以信号x1(t)为例，对比ISBM，CSBM和S-CBM三种不同延拓方法得到的极值点和包络线，如图4所示。

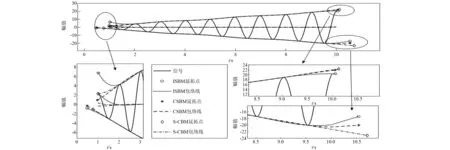
图4 基于三种不同方法的信号x1(t)的延拓点、上下包络线和平均包络线Fig.4 Extended points, upper envelops, lower envelopes and mean envelopes of signal x1(t) based on three different methods

从图4中可以看出，在该时间序列中，基于ISBM延拓的左端极大值点和右端极小值点没有很好地反映信号变化趋势。这是因为在求解延拓点所在直线的斜率时，ISBM没有考虑斜率变化过大带来的影响，导致延拓点出现较大误差。CSBM在该信号中延拓效果较好，但从信号左端放大的图像可以发现，CSBM延拓的局部极大值点位于信号第一个点(t1,x1)的下方，这虽然较好地反映了信号左端变化趋势，但却导致拓展的上包络线在局部区域位于信号下方，也就是不能很好地规避包络线过冲和欠冲[17]。而S-CBM由于综合了ISBM和CSBM两种方法的优势，延拓点则更好地反映了信号的变化趋势。

3.3 性能对比及分析

本节展示了六组测试信号在三种端点延拓方法下的EMD分解效果以及评价指标结果。为了更好地分析三种方法的性能，将三种端点延拓方法提取的IMF展现在同一张图中，其中最后一个IMF分量为剩余分量，代表信号的平均趋势。需要注意的是，由于EMD延拓算法的不同，其筛选得到的IMF数量可能不一样。表4、表5和表6分别示例了三种方法的正交指数、均方误差和能量误差对比情况。

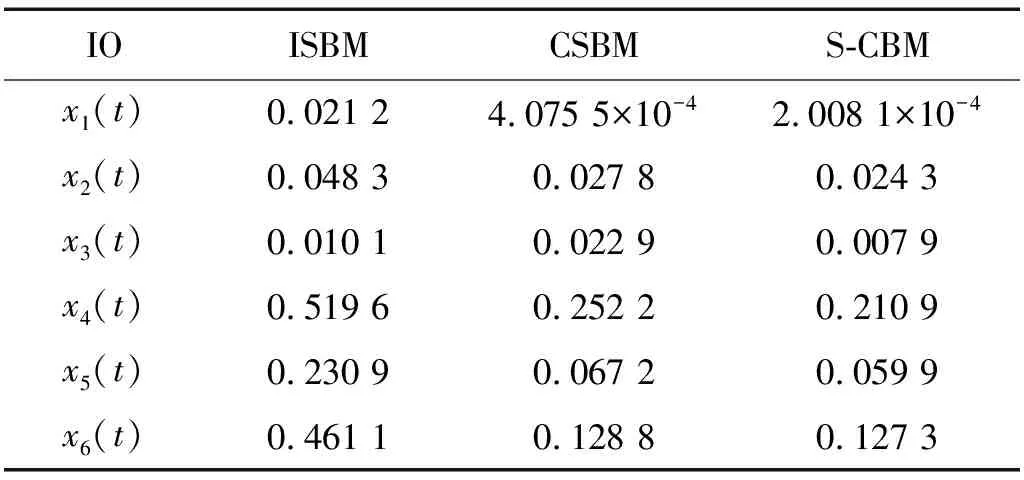
表4 三种不同延拓方法的IO结果对比Tab.4 IO results of the four signals by using EMD for three methods

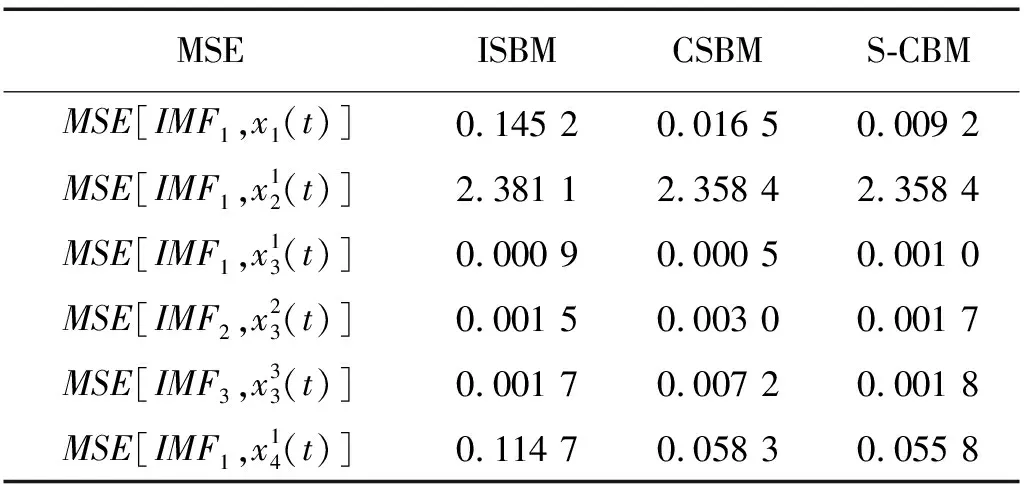
表5 三种不同延拓方法下的MSE结果对比Tab.5 MSE results of the four signals by using EMD for three methods

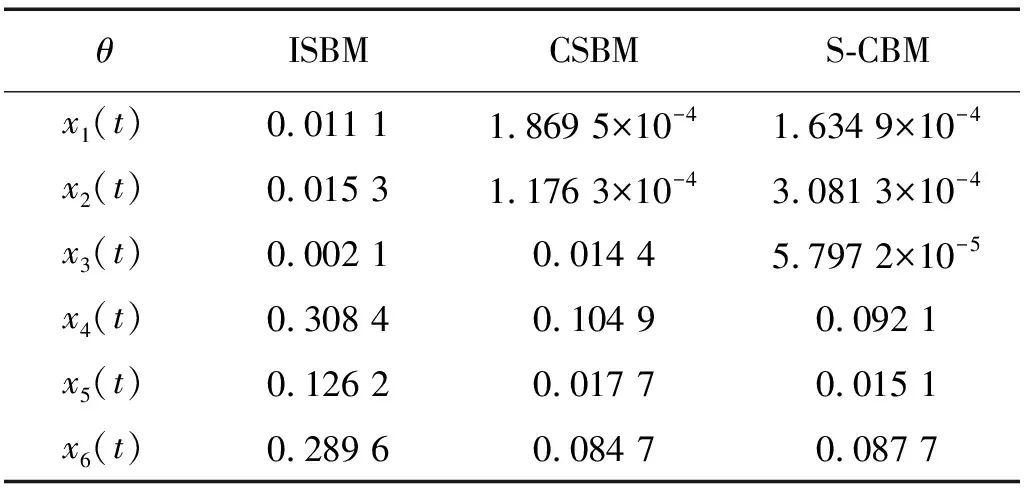
表6 三种不同延拓方法下的θ结果对比Tab.6 θ results of the four signals by using EMD for three methods

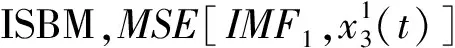
从定性的角度，对比图5～图10中三种延拓算法的EMD分解结果，发现：各信号所提取的IMF分量在两端端点处的波动幅度越大，则端点效应越明显，对应的端点延拓算法性能就越不足。下面以信号x1(t)为例，结合该信号的分解结果(见图5)来展开说明。对比图5中的IMF1，发现ISBM提取的IMF1在左侧端点处波动幅度明显大于CSBM和S-CBM所提取的结果，这一现象在后续的IMF2，IMF3及IMF4中表现更为突出。也就是说，对于x1(t)，ISBM所提取的各IMF分量在两端的波动幅度明显大于CSBM和S-CBM所提取结果的波动幅度。相对而言，CSBM和S-CBM两种方法提取的IMF波动幅度较小。但由于S-CBM集成了ISBM和CSBM的优点，相比较而言，S-CBM的波动幅度要小于CSBM。其他信号提取结果可以类似分析。显然，所提取的IMF波动幅度越大，则端点效应越明显，所以，定性分析的结果与前面定量分析的结果是一致和吻合的。

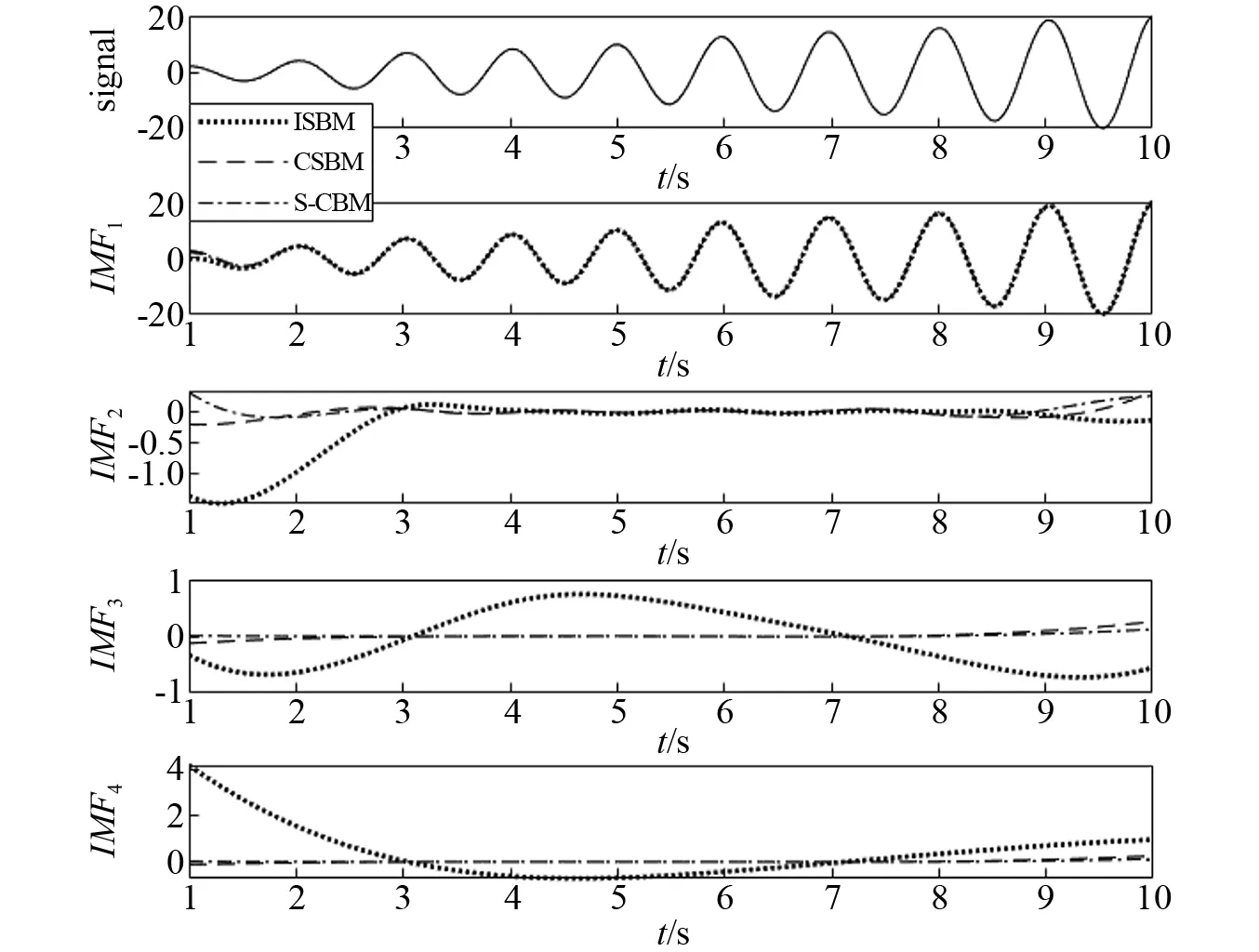
图5 基于三种方法的x1(t) EMD分解结果Fig.5 EMD results of x1(t) based on the three methods

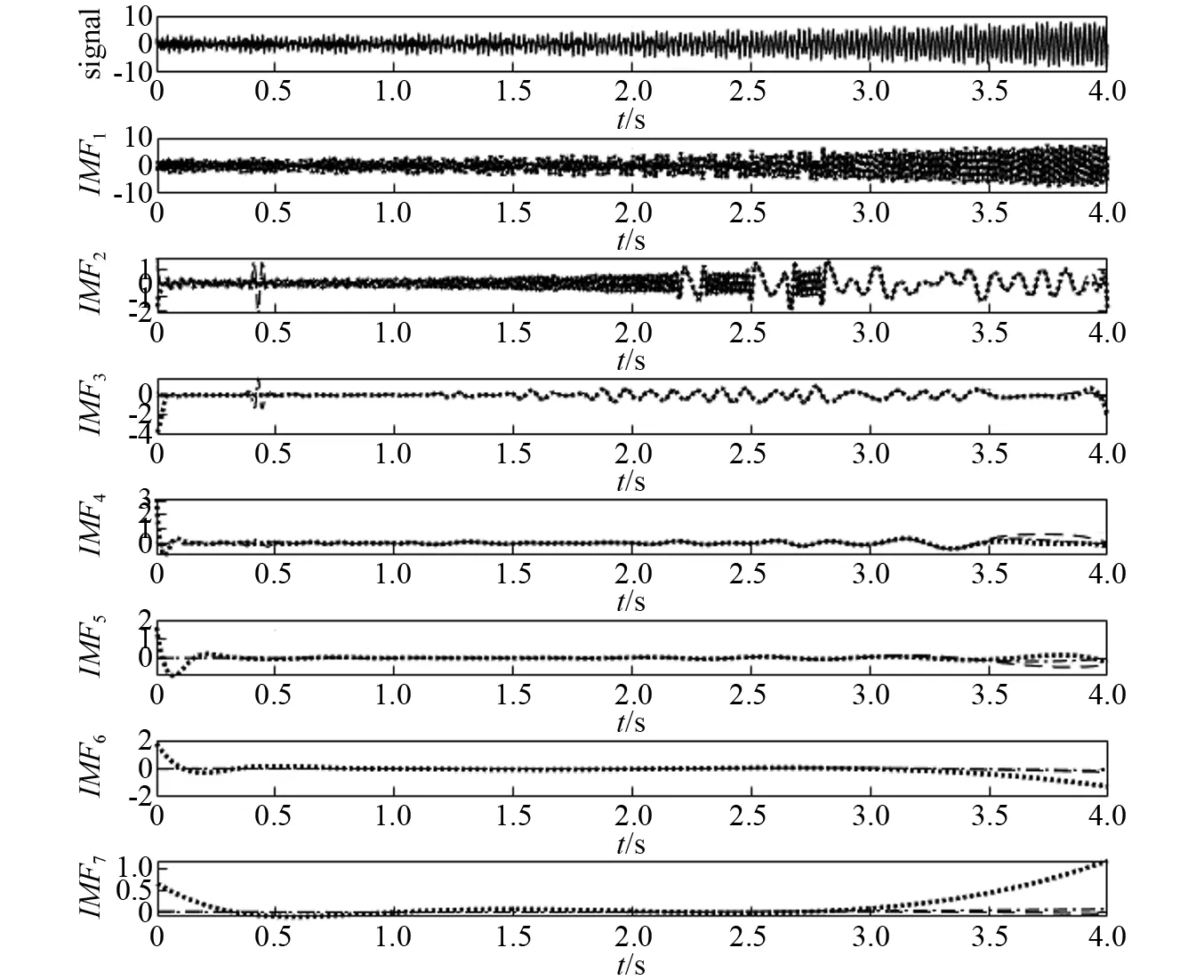
图6 基于三种方法的x2(t) EMD分解结果Fig.6 EMD results of x2(t) based on the three methods

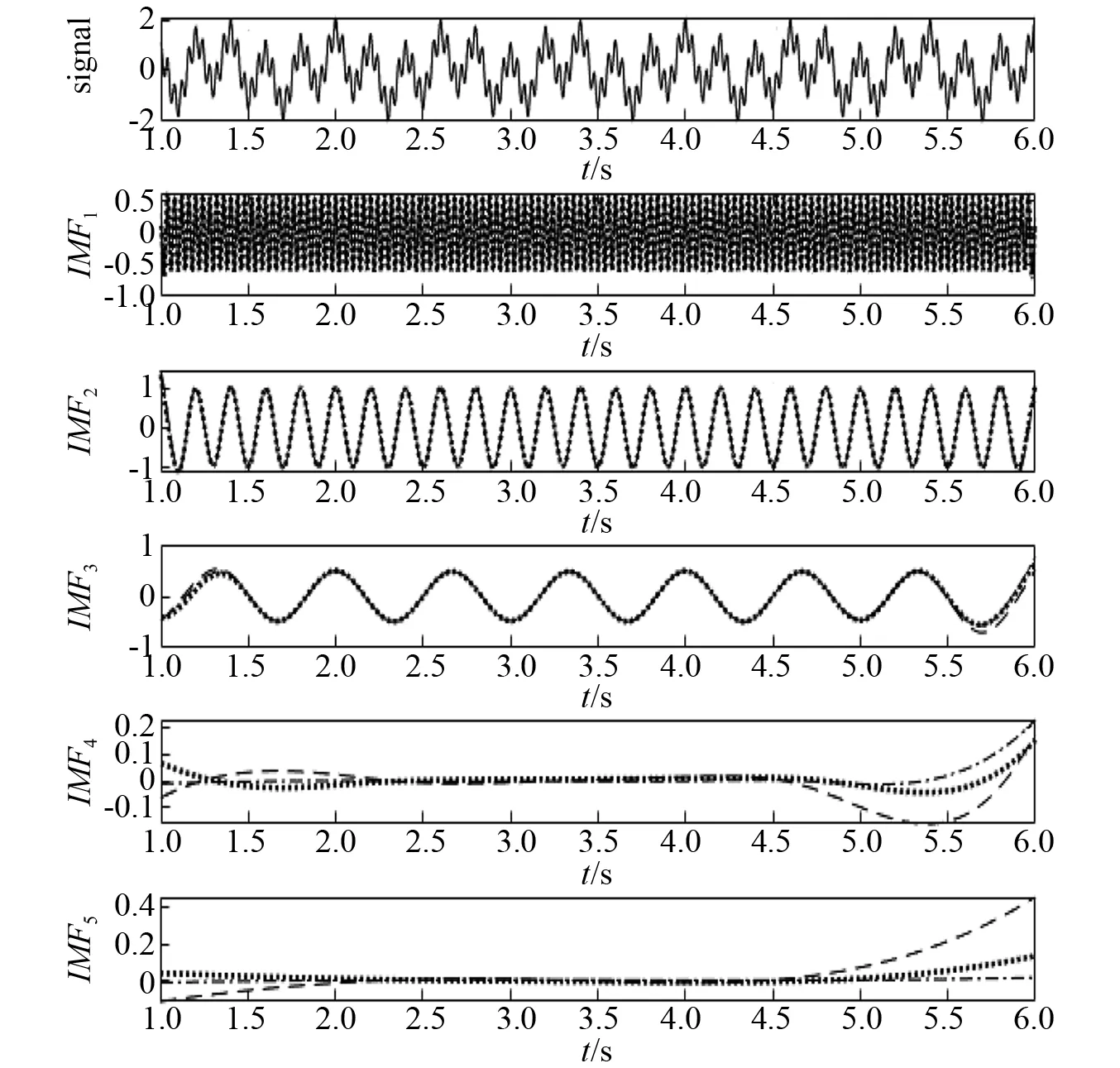
图7 基于三种方法的x3(t) EMD分解结果Fig.7 EMD results of x3(t) based on the three methods

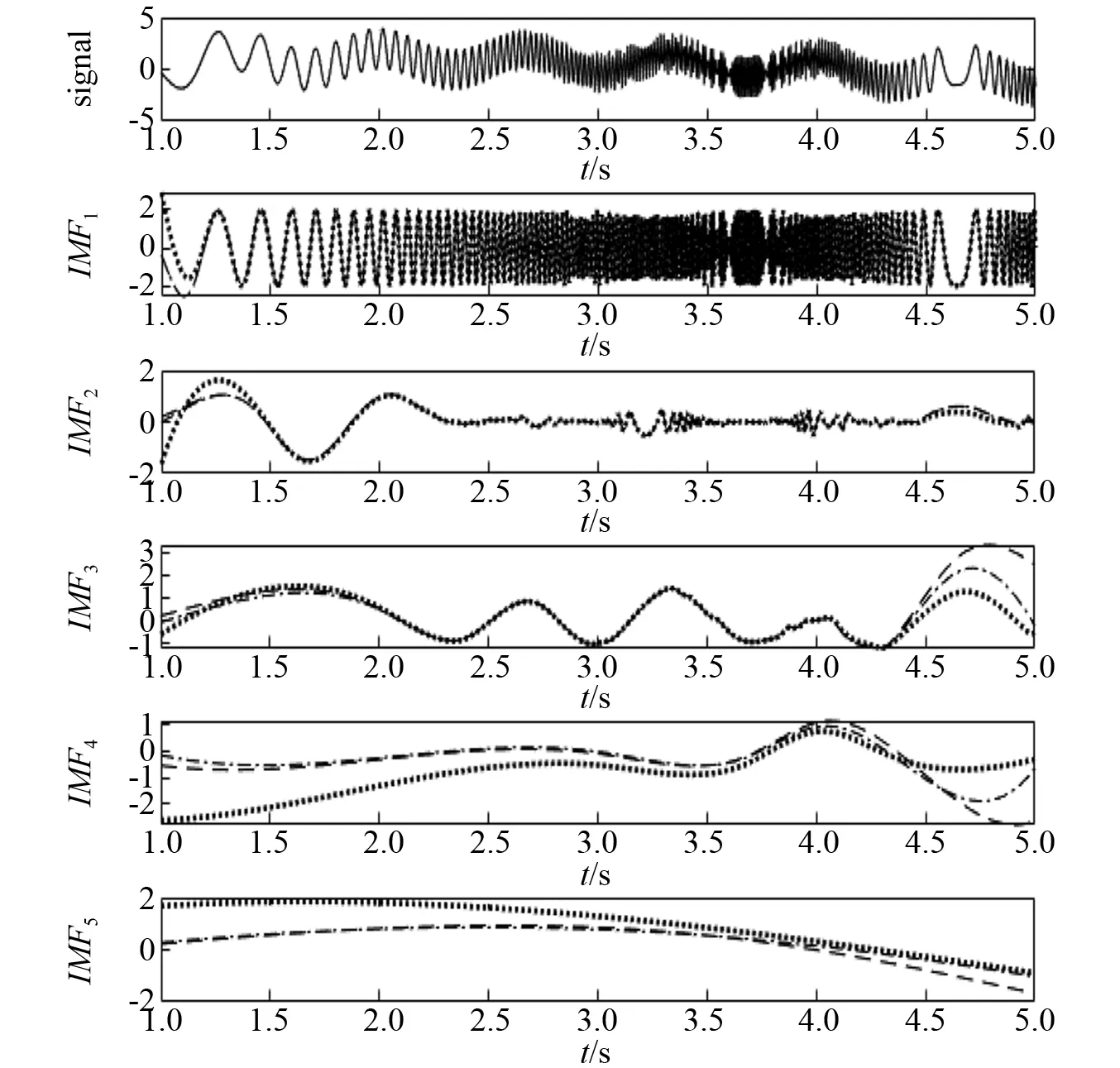
图8 基于三种方法的x4(t) EMD分解结果Fig.8 EMD results of x4(t) based on the three methods

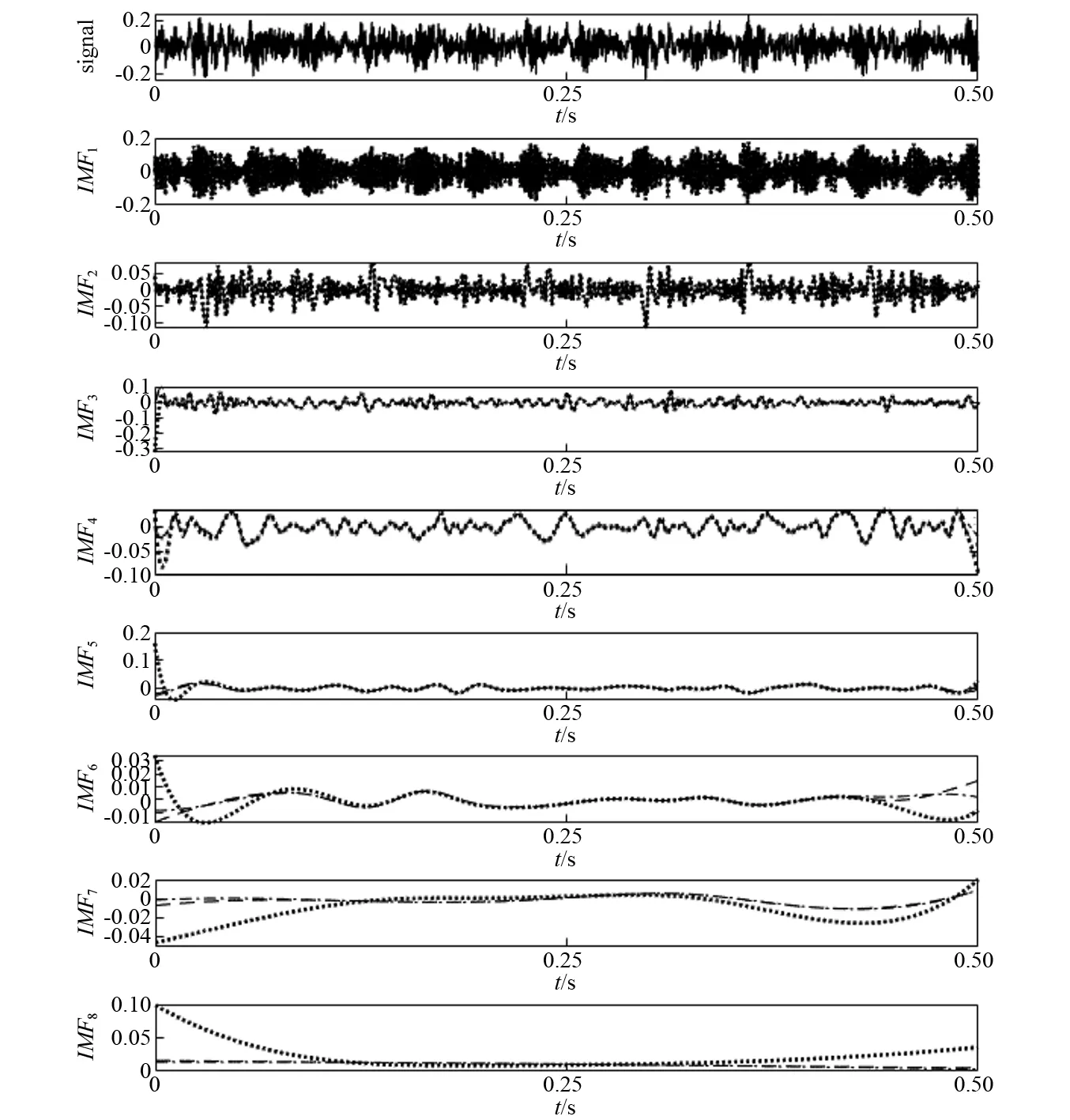
图9 基于三种方法的x5(t) EMD分解结果Fig.9 EMD results of x5(t) based on the three methods

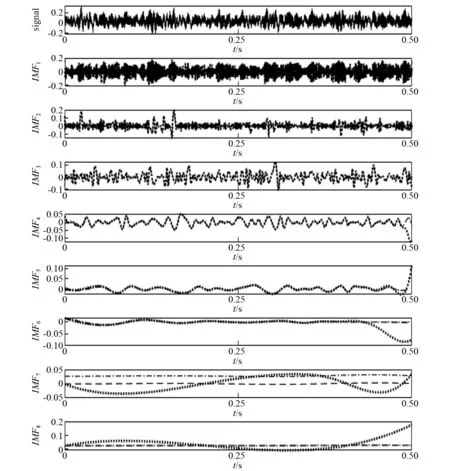
图10 基于三种方法的x6(t) EMD分解结果Fig.10 EMD results of x6(t) based on the three methods

总体而言，试验对比结果表明：本文所提出的方法在性能上整体优于CSBM和ISBM。

4 结 论

本文针对CSBM延拓算法存在的缺陷，提出了基于斜率和三次样条相结合的端点延拓方法。该方法根据信号端点的变化趋势，并利用延拓前后包络线在公共区域完全重合的特性唯一确定延拓点位置，克服了CSBM在设置延拓点坐标时没有充分考虑信号趋势的不足，进而使延拓点坐标确定更合理。模拟和实际工程应用测试信号以及IO，MSE和θ三个度量指标的试验对比结果表明：本文提出的方法在抑制端点效应上总体性能更好。这也是我们在前期工作基础上，对CSBM中延拓点坐标选取的一种完善和改进。需要说明的是，本文所提方法涉及的有关理论我们在Xu等的研究中已展开了详细论述。

针对本文工作，下一步的研究主题主要包括如下两个方面：一是EMD提取IMF的迭代收敛理论证明，进而为端点延拓算法设计提供理论指导；二是端点延拓算法设计的数学实质揭示。