基于概率幅值解调的机械故障诊断方法研究
李志农, 刘晓雨, 许巧巧, 谷士鹏, 马亚平
(1.南昌航空大学 无损检测技术教育部重点实验室,南昌 330063; 2.中国飞行试验研究院,西安 710089)
解调是将一个信号进行分解的过程,而分解则是主要将其分解成是正的缓慢变化的包络线和正负皆可的快速变化的载波,两者之间时间尺度不一样,故而分解的一维信号需要用两个不同重量级的时间尺度表示。在机械故障诊断中,最传统的解调是Hilbert包络解调[1-3],其基本原理是由含有解调信号的原始信号和该原始信号的Hilbert变换构成一个解析信号,分别构成解析信号的实部和虚部,求该解析信号幅值得到该原始信号的包络信号,再对包络信号进行频谱分析得到其包络谱。然而,在传统的Hilbert包络解调中存在有三个缺点:一是包络线的时间尺度常常和期望的时间尺度不一样;二是没有参数可以确定时间,因此,它不能控制时间尺度;三是在通常情况下,对载波的估计特别差。另外,在理论上,由于缺乏足够的先验知识,从本质上来说,传统的解调方法没有包含对不确定性的估计,因为这些方法既不重视先验信息的重要性,也不重视对不确定性的估计。
针对传统的Hilbert包络解调在机械故障诊断中存在的不足,有必要探讨新的解调方法。Turner等[4-9]提出了一种新型的解调方法——概率幅值解调(probability amplitude demodulation,PAD),他把解调看成一个推理问题。这种新解调方法使用概率理论。相较于传统方法,PAD具有明显的优越性,该方法在解调过程中运用已有的经验和理论对不确定性的问题进行反论证。不确定性信息可能也是有用的,当机械设备出现故障,往往可以通过估计包络线和载波变量中的不确定性来识别出故障的部位[10-12]。在此,基于PAD的独特优势,本文将该方法引入到机械故障诊断中,提出了一种基于概率幅值解调的机械故障诊断方法,并进行仿真和试验验证,同时,与传统的Hilbert包络解调方法进行对比研究。本文的研究为机械设备发生故障时出现的大量调幅调频信号的处理提供了一种新的方法。
1 概率解调的理论和算法
解调过程中,最主要的是寻找有效载波。尤其是在缓慢包络过程中,则需要在无穷多中选择一个有效分解,直接用传统方法寻找,则无法运用先验信息,加大选择难度,而运用概率幅值解调方法则是充分运用先验信息,使选择分解得到简化。
为充分利用此方法,需要建立前置模型,建立该模型是为了充分的收集并利用先验信息,并由此完成推理,达到解调之目的。
1.1 前置模型
将概率幅值调制的前置模型设置为yt=atct。式中:at为缓慢变化的包络线;ct为快速变化的实值载波;yt为调制信号。
at有多种方法得到,为简便计算,我们先假定载波为一白噪声,将其进行缓慢变化的实值过程实现,这个包络处理的过程我们称之为转换原始包络xt,然后运用指数函数变换进行实现。即:at=expxt。
此包络线一般是根据逐渐变化的过程进行选取,但为了方便后续分析,在此所选取的模型是AR(1)模型,为了方便,需要将该模型进行归一化处理,其具体处理过程如下
(1)
(2)
(3)
yt=ctat=ctexpxt
(4)
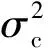
(5)
在式(1)~式(4)所描述的模型中,当调制信号与新包络线两者之间具有显著相关性时,信号yt相对at,ct的条件概率可表述为
p(yt|at,ct)=δ(yt-ctat)
(6)
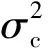

(7)
ct=yt/at
(8)
这种简单PAD(Simple-PAD,S-PAD)从根本上来说属于随机波动模型范畴,在GARCH模型中,不同步长上的幅值由前一步长数据及其幅值所决定,基于GARCH模型所得随机波动模型可表述为
(9)
对机械故障数据来说,由于在此处引入了随机幅值变量参数,因此模型的应用和相关变量的添加也更为灵活,有利于实现各种机械故障数据的处理,同时可将基本的随机波动模型推广到参数估计之中,可通过极大似然法等完成推广。
概率幅值解调与观测噪声的模型有关,可通过高斯过程模型来对特定情形下的时变方差进行估计。
1.2 推 理
S-PAD模型中,最为关键的是调制信号的概率分布计算,在计算时具体表达式为:
p(y1∶T,X0∶T|θ)=
(10)
式中:xt为包络线;ct为载波;at为新的包络线;xt为原始包络。
根据式(10)可知,该模型包含两个非线性变换,分别为:①xt和ct的积;②at和xt之间的指数变换,即at=expxt。
由式(10)可知,若要直接计算联合概率分布,则需要耗费大量时间计算,为避免出现求解过程过于冗杂,在实践中通常使用近似法予以求解。近似法求解的公式为
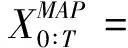
(11)
2 仿真研究
2.1 调幅调频信号仿真
设调幅调频信号模型为
x(t)=A[1+Bcos(2πfnt)]cos[2πfzt+βsin(2πfnt)](12)
式中:A为信号的幅值;fn为调制频率;fz为载波频率;B为调幅的调制指数;β为调频的调制系数。
除此之外,在上述调幅调频信号模型之中,调幅以及调频所采用的调制源相同。在此处设定采样频率为2 048 Hz,采样点数为10 240。完成上述参数的定义和取值:A=1,B=1,fn=25 Hz,fz=400 Hz,β=0.5, 解调的时间尺度l=5。
在开始进行求解分析之前,需完成数据的归一化和规范化处理。仿真信号的时域波形如图1所示,为了清晰,图2给出了仿真信号在0~0.5 s内的局部放大图。在基于上述模型进行概率幅值解调,完成了调幅信号载波和幅值的分解,这样就实现了单独成像。图3为包络线部分。其0~0.5 s内的局部放大图如图4所示。图5为载波部分。其0~0.5 s内的局部放大图如图6所示。图7、图8分别为仿真信号经过概率幅值解调后的载波部分和包络线部分。由图3和图7可知,解调后的包络线部分幅值信号会变小。由图5和图8可知,完成概率幅值解调后载波部分幅值会变大。进一步分析,从整体上来说,调幅信号的能量稳定性较好,且经过解调之后载波部分能量相较于调制之前更大,幅值部分相较于调制之前更小,由此可知,概率幅值解调可实现载波能量转移,实现载波和幅值的互相分离。
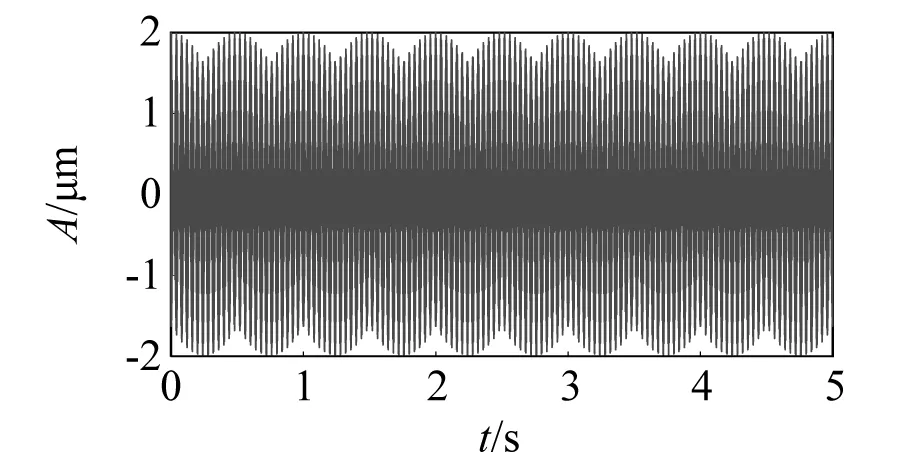
图1 调幅调频信号的时域波形图Fig.1 Time-domain waveform of AM and FM signals
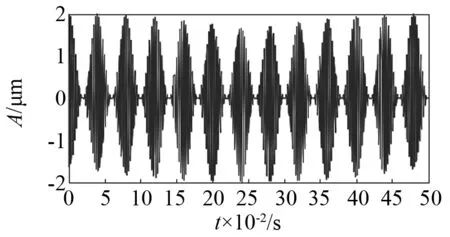
图2 时域波形图的局部放大图Fig.2 The partial enlargement of time-domain waveform

图3 调幅调频信号的包络线部分Fig.3 Envelope part of AM and FM signals
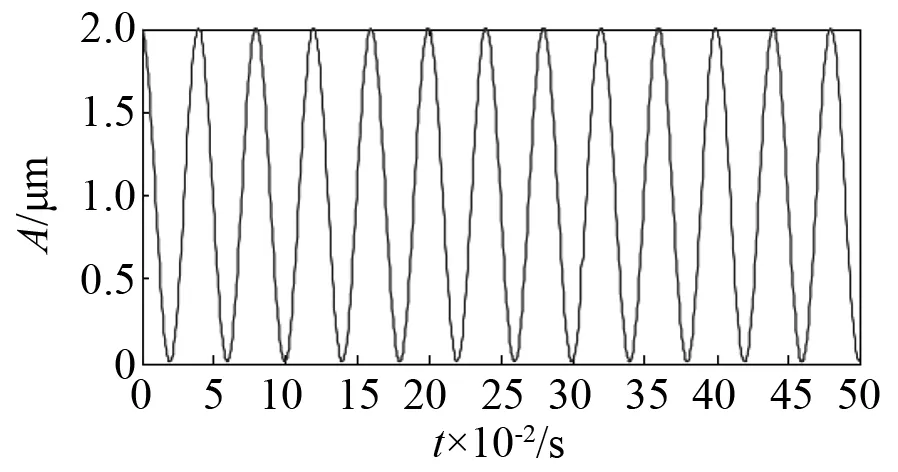
图4 包络线的局部放大图Fig.4 The partial enlargemen of envelope

图5 调幅调频信号的载波部分Fig.5 Carrier part of AM and FM signals
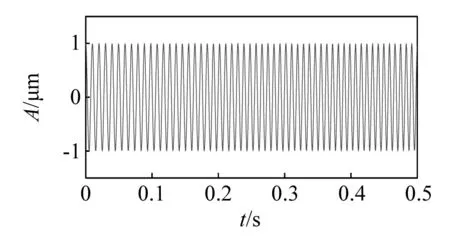
图6 载波的局部放大图Fig.6 The partial enlargement of carrier

图7 经过概率幅值解调后的包络线Fig.7 The envelope after demodulation with probability amplitude
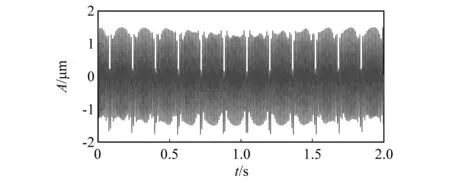
图8 经过概率幅值解调后的载波Fig.8 The envelope after demodulation with probability amplitude
图9、图10分别为原始数据和概率幅值经过解调后的包络线与载波。由图9可知,可以得到原始数据经过解调之后的包络线与原始数据之间具有良好的重合度和吻合性;由图10可知,解调后的载波信号可以承载原数据。图11为调幅调频信号的频谱图,分析可知调幅调频信号的调制频率fn=25 Hz。图12为解调后的频谱图,由图12可知,调幅调频信号的调制频率即fn=25 Hz以及调制频率的二倍频、三倍频、四倍频、五倍频、七倍频。
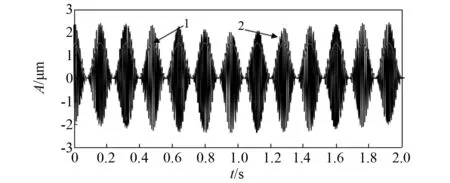
注:1为经过概率幅值解调后的包络线;2为原数据。图9 原数据和经过概率幅值解调后的包络线Fig.9 Original data and envelope after demodulation with probability amplitude
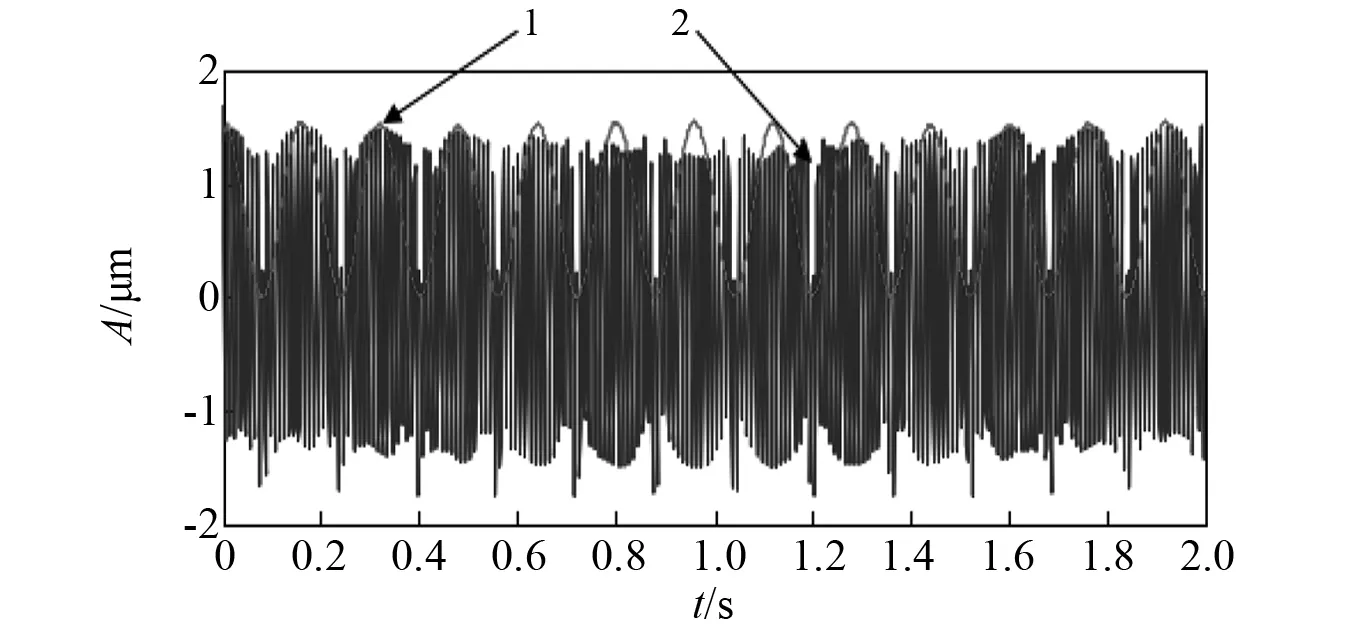
注:1为经过概率幅值解调后的包络线;2为原数据。图10 经过概率幅值解调后的包络线和载波Fig.10 Envelope and carrier after demodulation with probability amplitude

图11 调幅调频信号的频谱图Fig.11 Spectrum diagram of AM and FM signals
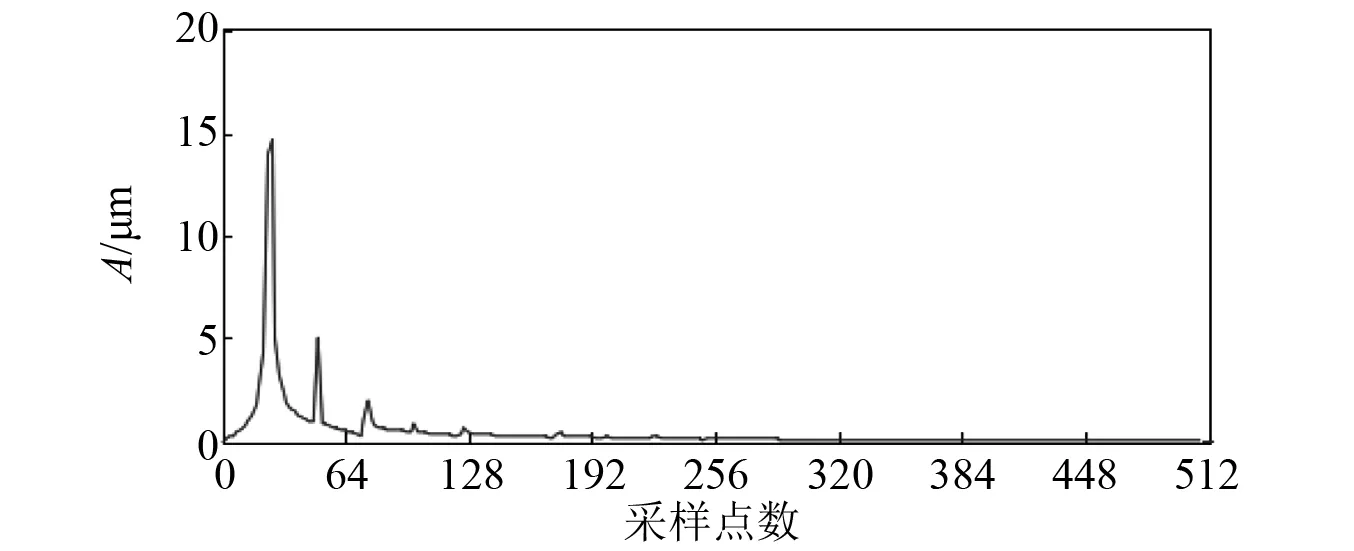
图12 调幅调频信号经过概率幅值解调后的频谱图Fig.12 Spectrum diagram of AM and FM signals after probability amplitude demodulation
2.2 概率幅值解调与希尔伯特包络对比分析
为了验证概率幅值解调的优越性,将其与希尔伯特包络法进行比较。为保证其准确性,运用对照试验法,声音信号保持不变,通过上述两种方法进行处理,对处理过程进行仿真分析[13],设定采样频率为16 000 Hz。
先使用希尔伯特包络法进行处理,将采样频率设为16 000 Hz,然后对其进行仿真。为方便后面进行分析出来,先绘制出时域原信号及其频谱,分别如图13和图14所示。
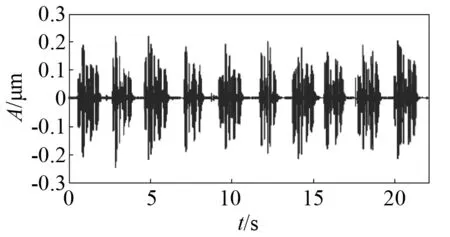
图13 原信号时域波形图Fig.13 Time domain waveform of original signal

图14 原信号频谱Fig.14 The original signal spectrum
在进行滤波器设计时,其过程如下:首先要对数据进行归一化处理,保证数据平稳化,必须设计上下截止频率,如此能绘制出如图15的带通滤波器频谱图,范围为:128/采样频率~4 096/采样频率。需注意选取上下截至频率,他是能影响滤波性能的决定性因素。其次需要完成滤波处理,由此可得到新的频域信号,由此可得到滤波后频谱,如图16所示。随后对得到的新频率信号进行反变换,即可得到时域信号x1,并通过变换求取时域信号的包络线,由此得到包络线及其频谱,如图17和图18所示。通过滤波之后绘制希尔伯特包络谱如图19所示。

图15 滤波器频谱Fig.15 Filter frequency spectrum

图16 原信号频域滤波之后的频谱Fig.16 After the original signal frequency domain filtering spectrum
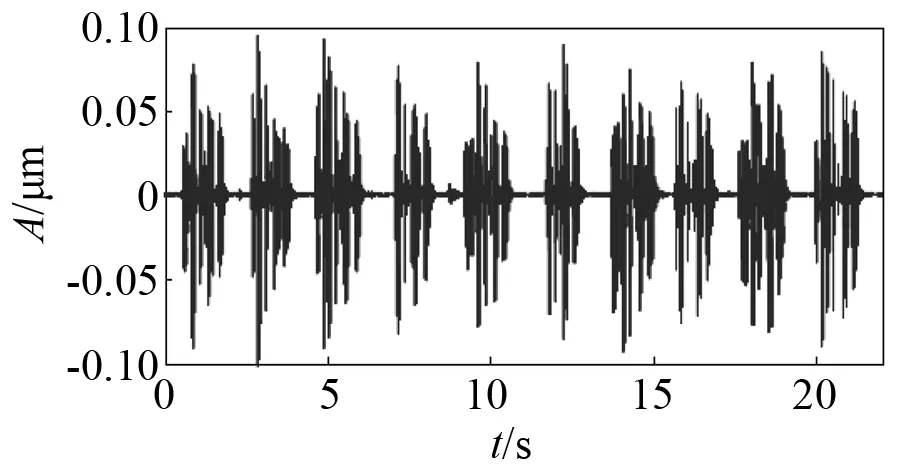
图17 滤波之后的时域信号Fig.17 Time domain signal after filtering
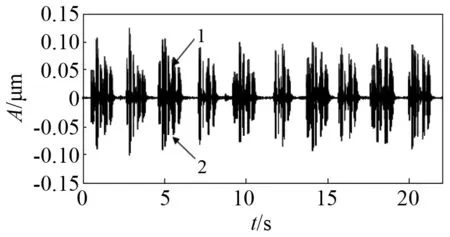
注:1为经过概率幅值解调后的包络线;2为原数据。图18 经过滤波之后的时域信号x1和包络线Fig.18 After filtering in the time domain signal and envelope x1
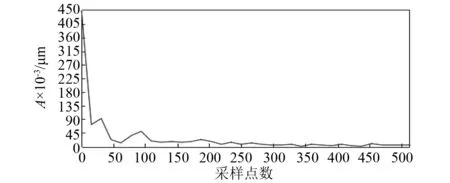
图19 包络谱Fig.19 The spectral envelope
对图13和图17进行分析可知,通过希尔伯特法处理得到的时域原信号和滤波之后的信号具有一定的相似性,由此可论证滤波信号的滤波性能受截止频率的影响明显。分析可知,当频率一定时原信号和滤波信号频谱有一定相似性,即在相应区间之内,两信号频谱之间能量分布具有相似性。如此,仅从频谱分析,滤波器设计符合要求,滤波效果也符合试验结果。对图18进行分析,得出包络线具有良好的拟合效果,符合本试验目的。分析图19可知,曲线平滑,由此可知能量在对应区间范围内的分布较为稳定均匀。
从仿真得到的一系列效果图,可以得到希尔伯特包络法的优势在于频域方向。接下来,将通过概率幅值解调法对上述仿真信号进行处理,经过概率幅值解调后的包络线如图20所示。由图20可知,经过概率幅值解调后包络线和原数据具有较好的拟合度,既没有过包络,也没有欠包络。由图21可知,包络线较为平滑稳定,没有尖刻。图22为经过概率幅值解调后得到的载波,由图22可知,时域上载波分布均匀。对比原信号的频谱(如图23所示)和经过概率幅值解调后的频谱(如图24所示)可知,此解调前后的频谱十分相似。
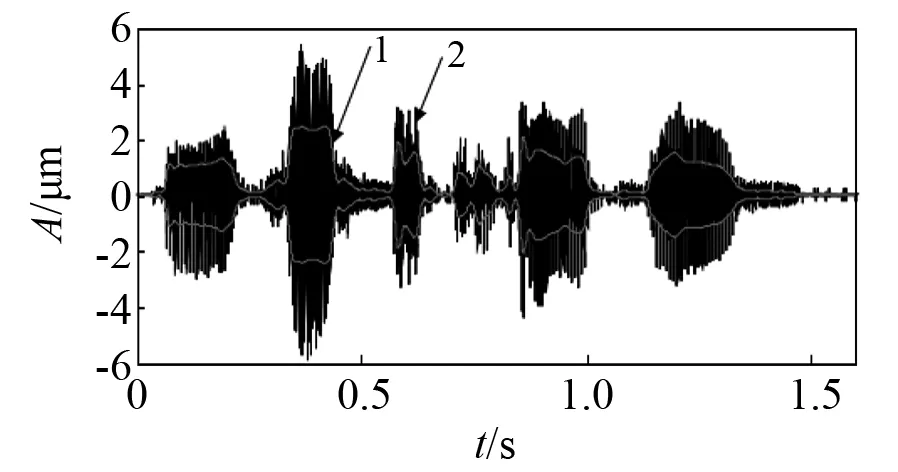
注:1为经过概率幅值解调后的包络线;2为原数据。图20 原信号和经过概率幅值解调后的包络线Fig.20 The original signal and after demodulation probability amplitude envelope
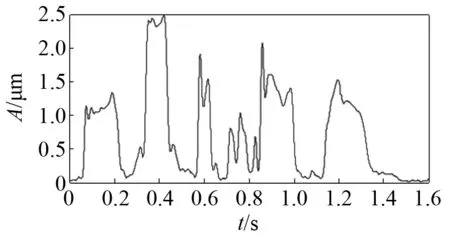
图21 经过概率幅值解调后的包络线Fig.21 After demodulation probability amplitude envelope
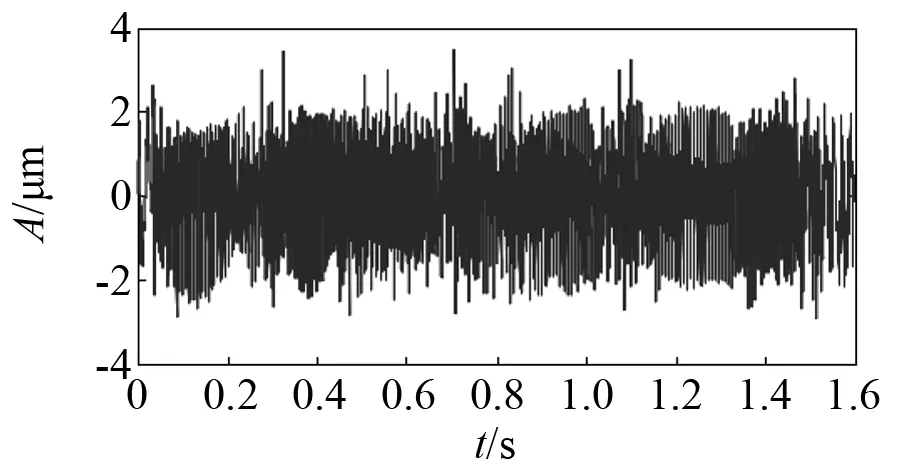
图22 经过概率幅值解调后的载波Fig.22 After demodulation probability amplitude of the carrier
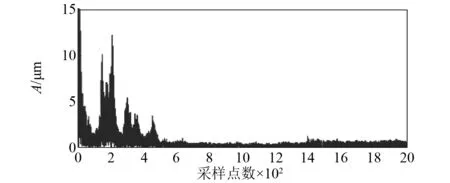
图23 原信号频谱Fig.23 Original signal spectrum

图24 概率幅值解调后的包络线频谱Fig.24 Nvelope spectrum after probability amplitude demodulation
3 试验研究
3.1 美国凯斯西储大学的轴承故障试验验证
为了验证提出的方法的有效性,这里,先利用美国凯斯西储大学电气工程与计算机科学系的轴承试验数据进行验证。其试验装置如图25所示。试验设备包含电机、扭矩传感器、功率计以及相关电控设备等。设置的滚动轴承具有单点故障,故障直径尺寸分别为0.017 78 cm、0.035 56 cm、0.053 34 cm、0.071 12 cm、0.101 6 cm[14]。其中前三种故障轴承对应为三个SKF轴承,后两种故障轴承对应为NTN轴承。

图25 试验与采集装置Fig.25 Experiment and collection device
试验中,采集振动信号是需要对加速度信号进行采集,选择的是加速度传感器,将其安装在试验装置的壳体上。根据已有的研究成果可知,有部分试验传感器安装位置为支承盘上。通过记录器采集振动信号,在本文中,选择内圈故障数据为样本进行分析,设定采样频率为12 000 Hz,发动机转速为1 730 r/min,转频为fr=28.83 Hz,内圈故障特征频率为fi=155.70 Hz。内圈故障的时域波形如图26所示。采用概率幅值调制算法对其解调,如图27所示。对比图26和图27可知,解调前和解调后的时域波形有较高相似性,据此可知,该方法不会改变数据时域波形。图28为解调后的包络线部分。将解调后包络线和原信号同时绘制在图29上,由图29可知,在完成解调之后,原始数据和包络线具有较高的拟合度。解调后的载波部分如图30所示,可看到载波在时域上分布是均匀的。原信号、经过概率幅值解调后的信号以及经过概率幅值解调后的包络线的频谱图分别如图31、图32和图33所示。由图31、图32和图33可知,在进行调幅前后,频谱都在fr,2fr,fi,2fi,fi-fr,fi+fr处出现了峰值,由经过概率幅值解调后的载波频谱(如图34所示)可知,进行解调后的载波频谱在fr,2fr,3fr,fi,2fifi-fr处出现了峰值,故而可以得到驱动端轴承在fi=155.70 Hz处出现了内圈故障。
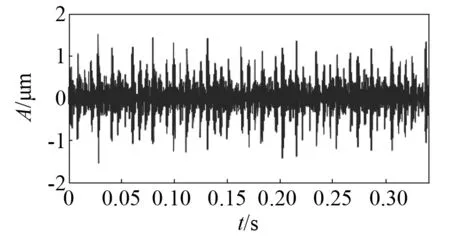
图26 原数据波形图Fig.26 Time domain waveform of original data

图27 经过简单的概率幅值解调后的原数据波形图Fig.27 Original data after simple demodulation of amplitude amplitude
图28 经过简单的概率幅值解调后的包络线部分Fig.28 The envelope section after simple probability amplitude demodulation

注:1为经过概率幅值解调后的包络线;2为原数据。图29 经过简单的概率幅值解调后的原数据和包络线部分Fig.29 The original data and envelope after a simple demodulation of amplitude amplitude

图30 经过概率幅值解调后的载波部分Fig.30 Carrier after demodulation with probability amplitude
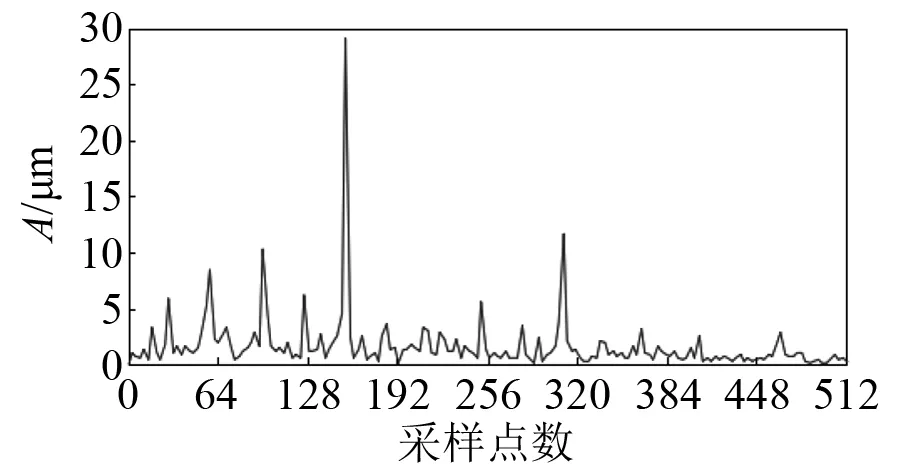
图31 原数据的频谱图Fig.31 Spectrogram of original data

图32 经过概率幅值解调后的原数据的频谱图Fig.32 Spectral diagram of the original data after probability amplitude demodulation
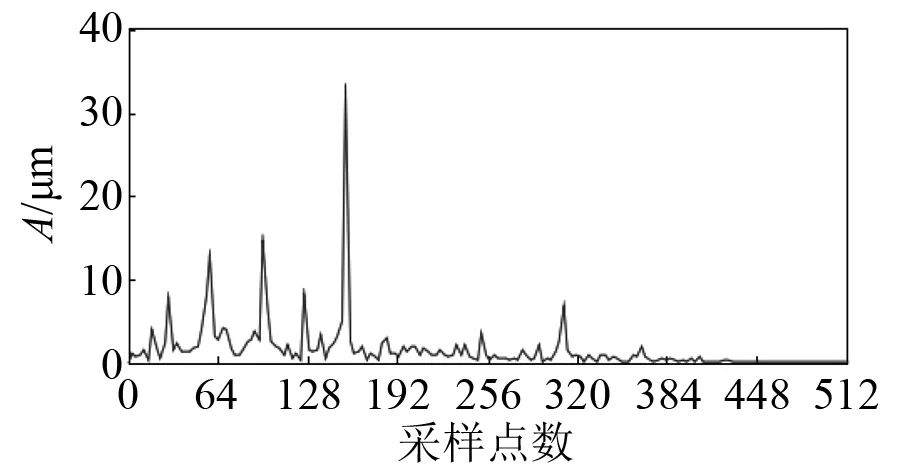
图33 经过概率幅值解调后的包络线频谱图Fig.33 The envelope spectrum after demodulation with probability amplitude
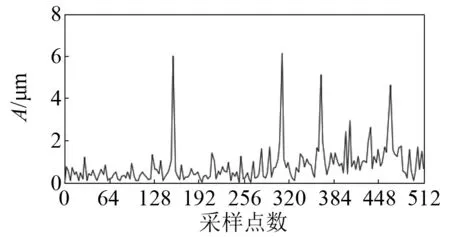
图34 经过概率幅值解调后的载波频谱图Fig.34 Carrier spectrum after demodulation with probability amplitude
3.2 机械故障仿真试验台的轴承故障试验验证
机械故障仿真试验台包含驱动电机、联轴器、轴系(含圆柱形转盘)、轴承、控制调速器。本试验仅涉及轴承故障模拟,所以将末端连接皮带拆除。试验中左侧电机通过联轴器与转轴连接并驱动转轴旋转,转速可以通过调速器调节,转轴两端各有轴承支撑,中间加装一个质量为1 kg的圆柱形转盘,将故障轴承设置在靠近电机的一端,另一端为健康轴承,如图35所示。

图35 试验与采集装置Fig.35 Experiment and collection device
本次试验总共采集三路信号:转速信号、竖直方向振动信号、水平方向振动信号。在电机输出轴上贴反光片,通过SM312LVMHS 传感器获取转速信号,另外选用两个IEPE型振动传感器,型号为PCB Model608A11,分别安装在轴承座的竖直和水平两个方向。在数据采集系统中选用的NI9234采集卡。
设定采样频率为25 600 Hz,发动机转速为1 800 r/min,其故障宽度为0.60 mm,基于此可计算转频为fr=30 Hz,内圈故障特征频率为fi=201.09 Hz。内圈故障的时域波形如图36所示。对内圈故障进行概率幅值解调,得到的解调信号如图37所示。将经过简单的概率幅值解调后的包络线和原数据绘制在图38上,由图39可知,解调前和解调后,原始数据和包络线具有较高的拟合度。图38为解调后的包络线部分,解调后的载波部分如图40所示,可看到载波在时域上分布是均匀的。图41、图42、图43给出了解调前后的频谱图。由图41、图42、图43可知,解调前后故障信号的频谱相似,解调后的包络线频谱和故障信号的频谱相似,其在fi,2fi出现了明显峰值,并且可发现在fi出现的峰值最大,可得到驱动端轴承在fi=201.09 Hz处出现了内圈故障。
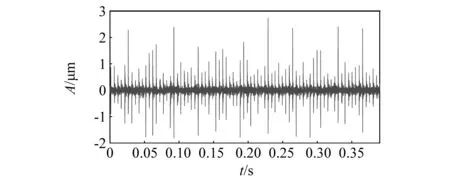
图36 原数据波形图Fig.36 Time domain waveform of original data

图37 经过简单的概率幅值解调后的原数据波形图Fig.37 Original data after simple demodulation of amplitude amplitude

图38 经过简单的概率幅值解调后的包络线部分Fig.38 The envelope section after simple probability amplitude demodulation
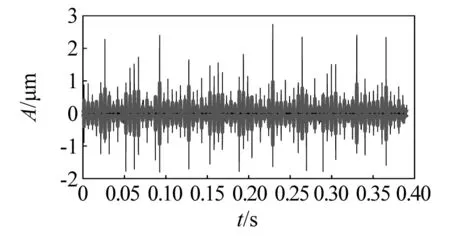
注:1为经过概率幅值解调后的包络线;2为原数据。图39 经过简单的概率幅值解调后的包络线和原数据Fig.39 The original data and envelope after a simple demodulation of amplitude amplitude
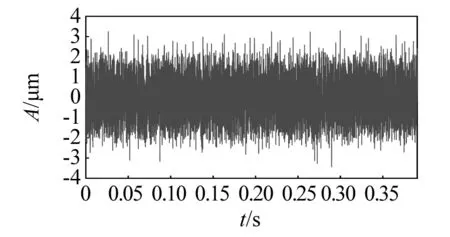
图40 经过概率幅值解调后的载波部分Fig.40 Carrier after demodulation with probabilityamplitude
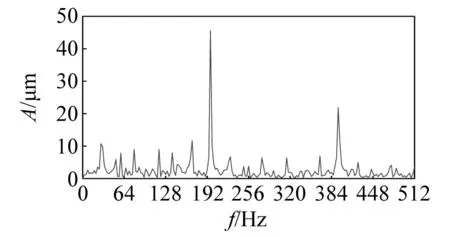
图41 原数据的频谱图Fig.41 Spectrogram of original data

图42 经过概率幅值解调后的原数据的频谱图Fig.42 Spectral diagram of the original data after probability amplitude demodulation

图43 经过概率幅值解调后的包络线频谱图Fig.43 The envelope spectrum after demodulation with probability amplitude
4 结 论
当机械设备出现故障时,往往存在大量的调幅调频信号,为了有效处理这些调幅调频信号,本项目将概率幅值解调引入到机械故障诊断中,提出了一种基于概率幅值解调的机械故障诊断方法,相较于传统方法而言,基于概率幅值解调的故障研究方法强调数学推理的应用,基于已有的经验和理论对可能的问题进行反论证,由此完成解调。同时,将提出的方法并与传统的希尔伯特包络解调进行对比研究。仿真结果表明,相较于传统Hilbert包络解调方法,概率幅值解调方法在解调准确性方面具有明显优势,能够弥补Hilber的缺点。通过概率幅值解调分解出来的包络线与原信号拟合地更加好,而通过希尔伯特包络解调出来的包络线与原信号的拟合程度没有前者好。最后,将提出的方法应用于滚动轴承故障诊断中。结果表明,概率幅值解调方法是非常有效性的,能够提取出滚动轴承故障特征频率。

