水轮发电机组横/轴有限元振动分析

张雷克， 范宇宏， 张金剑， 马震岳， 王雪妮

(1. 太原理工大学 水利科学与工程学院，太原 030024；2. 大连理工大学 建设工程学部 水利工程学院，辽宁 大连 116023)

水轮发电机组的安全稳定运行与水电站经济效益以及所在电力系统稳定性密切相关。受水力、机械、电气等荷载影响，机组在运行过程中不可避免会产生振动，由多振源引发的水轮发电机组轴系非线性振动问题一直是本领域的研究热点与难点，在过去数十年间吸引国内外诸多学者开展了持续且深入的研究，并取得了丰硕的成果[1-12]。

利用集总参数法对包括转子、转轮、转轴及轴承在内的旋转部件予以简化从而推导系统运动微分方程是创建水轮发电机组轴系振动模型一种常见的手段。集总参数法原理简单，但公式冗长且建模中存在较多简化，不能完全反映轴系特征。相比之下，有限元法具有更高的计算精度和更广的适用范围。随着计算机技术的飞速发展，有限元法在机组建模与分析方面的优势逐步凸显。荣吉利等[13-14]采用有限元法研究了水轮发电机组轴系非线性振动特性，并着重讨论了附加质量效应的影响。文献[15-16]通过有限元方法，对机组进行了数值模拟分析，得到了临界频率及振型的模态分析结果。Betting等[17]提出了考虑发电机电磁力和水轮机不平衡水力的广义机组有限元模型，据此研究了系统固有频率及稳定性。肖黎等[18-21]所创建模型考虑因素更为全面，同时对细节的把控更为精细，故据此开展的机组轴系在多振源激励下动力学特性讨论能够较为全面地体现机组的运转特性，为大型水轮发电机组的振动设计和减振研究提供了重要理论支持。

借助有限元法，国内外学者在水轮发电机组轴系动态特性分析领域取得了令人瞩目的成就，不过需要指出的是，由于轴系横向振动问题突出，一直以来水电机组建模及相关动态特性讨论多围绕平面运动开展。在建模时主要集中于平面单节点4自由度(2个横向与2个扭转)，鲜有将轴向自由度纳入整体研究范畴。相关研究表明[22]，由于机组在轴向受约束相对有限，故其在该方向即便因较小激振力影响，亦有可能产生较大振动，进而给机组带来危害。文献[23]研究结果表明，机组因轴向水推力和轴向电磁力等轴向激励作用导致其轴向振动十分明显，应与横向和扭转等方向振动一样得到足够重视。此外，若将轴向与横向及扭转叠加在一起形成耦合效应，势必引起机组轴系产生不同的动态特性，因此十分有必要开展相关研究。

鉴于此，本文以单节点4自由度Euler梁为基础，通过引入轴向位移构建了单节点5自由度水电机组轴系有限元模型。在此基础上，利用Newmark-β和Newton-Raphson相结合方法分别讨论了考虑轴向自由度与否，以及考虑轴向电磁力与否等不同情况系统横向振动特性的差异。本文研究内容可为优化水电机组轴系模型并为机组早期振动控制提供参考。

1 水轮发电机组转子-轴承系统有限元模型

1.1 转子-轴承结构

水轮发电机组转子-轴承系统主要包括发电机转子、主轴和上、下导轴承等，其三维立体图如图1(a)所示。

图1(b)为转子-轴承系统有限元模型示意图，轴系共包含12个节点，分为11个轴段。其中，转子半径为0.6 m，位于轴段6上，上、下导轴承分别位于轴段4和轴段8位置。

为便于分析系统，对模型假设为：

(1) 定子假设为刚体，仅考虑转子振动；

(2) 在应变能计算中忽略剪切变形、横向位移对拉压变形能的影响。

此外，本文在模型构建时不考虑推力轴承影响。其原因在于：如考虑推力轴承作用，一方面，须将推力轴承本体及轴向水推力荷载纳入整体模型，从而增加建模的复杂性；另一方面，则不便于对考虑轴向自由度和轴向电磁力与否两种情况下系统横向振动特性差异进行辨识与分析。故本文在建模过程中忽略推力轴承作用。

对于机组各轴段，其两端节点自由度包括

(1)

式中：xA，yA，xB，yB，θxA，θyA，θxB，θyB为梁单元各节点在x，y方向上的位移和转角；zA，zB为梁单元各节点在z方向上的位移。

图1 转子-轴承系统示意图Fig.1 Diagram of rotor-bearing system

1.2 轴向电磁力

轴向电磁力作为引起系统轴向振动的关键外激励之一，其选取适当与否对于系统整体计算的准确性与稳定性具有十分重要的作用。目前，获取轴向电磁力的数学表述大致包括三种方式：基于传导纸模型、通过保角变换方法以及新的均方根方法。本文在此选用基于传导纸模型获得式(2)形式轴向电磁力[24]

(2)

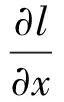
(3)

式中： Δz为轴向气隙偏心；δ为径向气隙长度。

1.3 水轮发电机组转子-轴承系统有限元模型

水轮发电机组转子-轴承系统运动微分方程为

(4)

式中：M，D，K分别为系统质量、阻尼和刚度矩阵；F_rub为发电机转子处碰摩力，其表达式详见张雷克等的研究；F_ump为发电机转子处考虑动、静偏心下UMP，其表达式详见Zhang等的研究；M_ump为发电机转子处电磁转矩，其表达式详见文献[26]；Fz为发电机转子处轴向电磁力。考虑轴向位移的单节点5自由度单元平移质量矩阵、转动质量矩阵、陀螺力矩矩阵和刚度矩阵具体形式分别为

(5)

(6)

(7)

(8)

式中：l为单元长度；EI为抗弯刚度；μ为单位长度质量；r为单元半径。

本文采用瑞利阻尼建立系统阻尼矩阵，其形式为

C=αM+βK

(9)

其中，

式中：ξ1，ξ2为阻尼系数；ω1，ω2为转子的一、二阶临界转速。

2 数值计算分析

由于式(4)具有较强的非线性及非连续特性，故本文采用Newmark-β和Newton-Raphson相结合方法对系统运动微分方程进行求解。

计算所选用的主要参数如下：转子质量m1=1.44×105kg，转子转速ω=4 Hz，不平衡量的初始相位φ=0，转子半径R=0.6 m，转子长度L=0.3 m，定转子均匀气隙δ0=2×10-3m，空气磁导系数μ0=4×π×10-7H/m，发电机转子磁极对数p=12，内功率角ψ=30.64 rad，气隙基波磁动势系数kj=0.8，定子气隙基波磁动势Fsm=19 210 A。

2.1 轴向自由度对系统横向振动的影响

图2为Ij=345 A、静偏心δs=0.6×10-3m、动偏心δd=0.7×10-3m，krub=4.74×109N/m时，是否考虑轴向自由度转子系统随质量偏心变化的横向运动轨迹图。

从图中可以看出，随着e0的增加，转子横向位移呈递增趋势。不过，轴向自由度的加入对其运动轨迹形态及大小起到了明显改变作用。当e0=0.5×10-3m时，由于忽略轴向自由度的影响，如图2(a)所示，其运动轨迹表现为封闭不规则形状，最大振幅为0.76；当考虑轴向自由度后，转子运动形态为一规则封闭圆环，最大振幅为0.65。而在e0增至1.4×10-3m后，虽然在轴心轨迹形态方面几乎相同，但考虑轴向自由度与不考虑轴向自由度其振幅存在明显差异，相比于前者，因计及轴向自由度，转子横向振幅下降约15%。由此可见，轴向自由度的存在对抑制系统横向振动响应具有一定作用，特别是在振幅较大时较为明显。

注：ⅰ为不考虑轴向自由度；ⅱ为考虑轴向自由度。图2 不同质量偏心下系统响应的轨迹图Fig.2 Trajectory diagram of system response under different mass eccentricity

2.2 轴向电磁力对系统横向振动的影响

由2.1节分析可知，轴向自由度的加入对水电机组转子-轴承系统运动特性影响显著。本节在2.1节分析基础上，引入轴向电磁力激励，进一步讨论其存在与否对系统横振的影响。

图3为当Ij=345 A，Δz=2.0×10-3m，δd=0.7×10-3m，e0=0.30×10-3m，krub=4.79×109N/m时，是否考虑轴向电磁力转子系统随静偏心变化的横向运动轨迹图。从图3中可知，轴向电磁力的加入对转子横向运动轨迹起到了明显改变作用。当δs=0.56×10-3m时，由于忽略轴向电磁力的影响，如图3(a)所示，其运动轨迹表现为一规则封闭圆环，最大振幅为0.42；当考虑轴向电磁力后，转子运动形态为封闭不规则形状，最大振幅为0.52。而在δs增至2.0×10-3m后，虽然在轴心轨迹形态方面二者几乎相同，但考虑轴向电磁力与不考虑轴向电磁力其振幅存在明显差异，相比于前者，考虑轴向电磁力，转子横向振幅上升约29%。造成该现象的原因在于机组轴向受约束相对较弱，轴向不平衡电磁力引起系统出现轴向振动，并将其传递给发电机转子形成横/轴耦合振动效应，从而使机组转子部位横向振动加大。

注：ⅰ为不考虑轴向电磁力；ⅱ为考虑轴向电磁力。图3 不同静偏心下系统响应的轨迹图Fig.3 Trajectory diagram of system response under different static eccentricity

由Zhang等的研究可知，动偏心δd和静偏心δs与径向气隙长度δ密切相关。从式(2)和式(3)可以看出δ是影响轴向电磁力大小的关键参数之一，换言之，动、静偏心的改变不仅会造成系统横向UMP的变化，同时也会间接对轴向电磁力产生影响。因此，轴向电磁力和动、静偏心下的UMP存在复杂耦联关系。当δs增至某一程度后，由于动、静偏心下UMP和轴向电磁力的共同作用，造成转子横向振动加大，所以考虑轴向电磁力后转子横向位移出现明显增加。

3 结 论

针对机械和电磁故障引起的水轮发电机组轴系横、轴向耦合振动问题，本文以单节点4自由度Euler梁为基础，将轴向位移纳入轴系整体，推导并建立了单节点5自由度水电机组转子-轴承有限元模型，利用Newmark-β和Newton-Raphson相结合方法分别研究了是否考虑轴向自由度和轴向电磁力下质量偏心、静偏心对系统横向振动特性的影响，主要结论如下：

(1) 轴向自由度的加入对系统运动轨迹形态及大小起到了明显改变作用。同未考虑轴向自由度相比，转子运动轨迹相对减小。轴向自由度对抑制系统振动响应具有一定作用，特别是在振幅较大时较为明显。因此，从实际建模和改善系统运动特性角度出发，应充分考虑轴向自由度的影响。

(2) 轴向电磁力与动、静偏心下不平衡磁拉力形成电磁激励耦联效应，二者共同作用明显加大系统横向运动振幅。因此，出于对故障诊断识别及更为全面洞悉系统振动特性的需要，将轴向电磁激励纳入水电机组轴系整体建模范畴较为合理。