空气阻尼对网孔式弹性垫板动力学特性的影响研究

白彦博， 和振兴， 贠剑峰， 张 鹏， 王志璇

(兰州交通大学 机电工程学院，兰州 730070)

为了降低列车通过时振动产生的不利影响，轨道交通列车走行基础采用了大量的弹性垫板。文献[1-2]研究了扣件系统TPEE材质弹性垫板频变、幅变刚度对轮轨耦合系统随机振动的影响；文献[3]研究发现弹性垫板的刚度和阻尼是影响其动力学性能的关键参数，提高垫板阻尼对改善其减振能力是有利的；文献[4]研究表明减小道床刚度，会引起轨道系统振动的增大，隔振设计中应尽量避免轨道系统刚度取值过低。文献[5]通过锤击试验得出，在道床垫减振轨道的轨道板上添加配重，可以改善系统的振动特性；文献[6]提出了一种新型声子晶体隔震垫，并基于车辆-轨道耦合动力学模型将其与普通隔振垫的减振效果进行对比，得出新型声子减振垫具有更好的减振效果。文献[7]研究了CRTSⅢ型板式无砟轨道减振垫层铺设位置对减振效果的影响，得出减振垫层设置在底座板下时减振效果更优；文献[8-9]建立了车辆-有砟轨道-桥梁空间耦合动力学模型，研究发现采用减振垫可以降低有砟轨道的振动水平；文献[10]通过试验研究发现，采用弹性道床垫对抑制轨道下沉效果明显。

上述弹性垫一般由橡胶、聚氨酯等弹性材料制成。弹性垫板的刚度和阻尼是影响列车走行基础动力学性能的关键参数。提高阻尼对弹性垫板减振性能是有利的[11]，但目前弹性垫板的阻尼主要由材料性质决定，制约了普通弹性垫板阻尼的提高。研究团队提出了一种带高阻尼填充物的正六边形网孔式弹性垫板[12-13]，阻尼较普通弹性垫板可以提高60%左右，但对高阻尼填充物的材料要求较高，弹性垫板的加工成本较高。为了探索提高弹性垫板阻尼的新途径，研究团队在既有研究的基础上进一步提出了一种具有空气阻尼的网孔式减振垫板结构[14]。本文以道床用弹性垫板为例，研究了节流孔孔径、气室体积比对空气阻尼网孔式弹性垫板刚度和阻尼特性的影响规律。同时，将空气阻尼网孔式弹性垫板与普通网孔式弹性垫板和填充高阻尼材料网孔式弹性垫板进行对比。

1 流固耦合模型

1.1 空气阻尼网孔式弹性垫板单元模型

空气阻尼网孔式弹性垫板上部为强变形层，由弹性较大的材料制成；下部为弱变形层，由弹性很小的材料制成。正六边形网孔式结构的空腔分别在强变形层形成主气室，在弱变形层形成附气室，两气室间通过节流孔联通[15]。其结构如图1所示。该弹性垫板主要起承受垂向载荷的作用，假设对弹性垫层施加固定频率的循环垂向动载荷，强变形层将会产生较为明显的形变，弱变形层形变微弱。主气室内空气由于压缩的作用经节流孔流入附气室中，当气体流经节流孔时会产生阻尼从而起到缓冲振动的效果。

图1 空气阻尼网孔式弹性垫板整板结构示意图Fig.1 Schematic diagram of the entire plate structure of the air damping mesh elastic backing plate

空气阻尼网孔式弹性垫板可以看成是由如图2所示的单个网孔式弹性垫板单元阵列而来，在弹性垫板整板上表面两网孔间的中线处截取一网孔单元，并划分六面体有限元网格，如图3所示。强变形层的杨氏模量和泊松比分别取0.15 MPa和0.050，弱变形层的杨氏模量和泊松比分别取0.21 MPa和0.499。

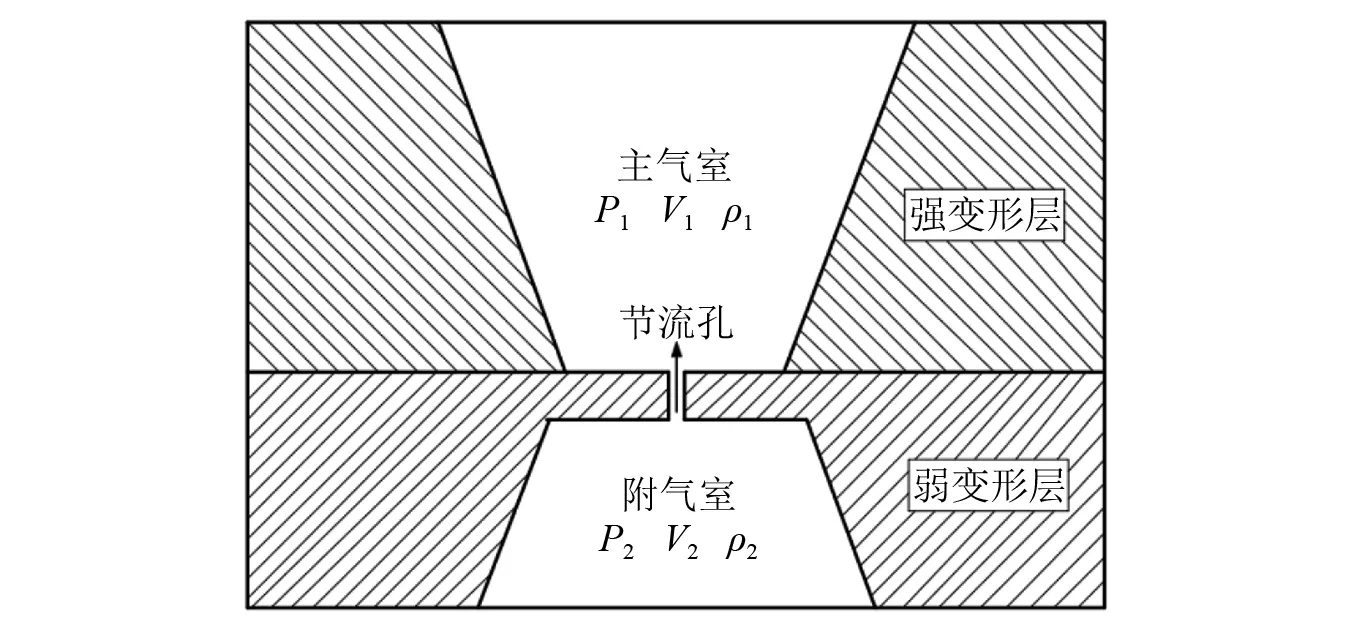
图2 空气阻尼网孔式弹性垫板单元结构示意图Fig.2 Schematic diagram of air damping mesh elastic backing plate unit structure

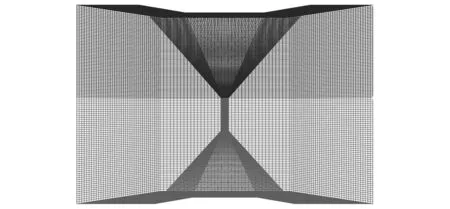
图3 空气阻尼网孔式弹性垫板单元有限元网格模型Fig.3 Finite element mesh model of air damping mesh elastic pad element

1.2 空气单元模型

建立与空气阻尼网孔式弹性垫板单元内部结构尺寸完全匹配的空气有限元模型，空气密度为1.29 kg/m3，黏度为1.82×10-5Pa·s，为了准确模拟空气阻尼的作用，空气单元的网格划分细密，一个空气单元的网格数为42 600，最小尺寸为0.5 μm，主要集中在节流孔位置。网格类型为六面实体，其有限元网格如图4所示。

图4 空气单元有限元网格模型Fig.4 Air element finite element mesh model

1.3 流固耦合边界

由于空气阻尼网孔式弹性垫板单元和空气单元的耦合作用仅发生在两者的相交界面上，故在弹性垫板单元网孔内接面和空气单元外接面分别定义两者的流固耦合界面，如图5所示。通过联合仿真可以实现两者的协同响应，该耦合界面可以模拟弹性垫板单元在考虑内部空气作用下产生变形。

图5 有限元模型耦合界面的定义Fig.5 Definition of finite element model coupling interface

1.4 动刚度和阻尼比

动刚度和阻尼比是弹性垫板的关键动力学参数，由于空气阻尼网孔式弹性垫板可以看成是由若干个结构相同的子单元阵列而成的，整板的动刚度和阻尼比由垫板单元决定。弹性垫板单元的动刚度Kd为[16]

(1)

式中：xm为最大荷载对应垂向位移与最小荷载对应垂向位移之间的差值；Fm为最大荷载与最小荷载之间的差值。

根据网孔式弹性垫板的结构特点可知，垫板上网孔间中线处的垂向面为受力对称面。受力对称面在加载垂向荷载后只有垂向形变，故沿着受力对称面切割的弹性垫板单元的垂向位移与弹性垫板整板的一致。由于弹性垫板单元的上表面面积是弹性垫板整板面积的1.32%，在弹性垫板上表面施加的是均布载荷，所以弹性垫板单元承受的载荷也为总载荷的1.32%，由式(1)可得弹性垫板整板与弹性垫板单元动刚度转换系数为1/1.32%=75.76，故弹性垫板整板的动刚度[17]Kz可表示为

Kz=75.76×Kd

(2)

弹性垫板单元结构的阻尼比与弹性垫板整板的阻尼比基本相近。弹性垫板整板阻尼比ζz为[18]

ζz≈ζd

(3)

(4)

(5)

式中：ζd为网孔式弹性垫板单元的阻尼比；δ为对数衰减率；An和An+k分别为网孔式弹性垫板单元自由振动衰减波形图中第n个和第n+k个波峰值；k为波峰间隔周期数 。

2 空气阻尼网孔式弹性垫板关键参数研究

2.1 垫板性能关键影响参数

为了明确影响空气阻尼网孔式弹性垫板单元刚度和阻尼的关键参数，将空气阻尼网孔式弹性垫板单元等效为一个质量-弹簧-阻尼系统，基于复刚度理论[19-20]得到系统的等效复刚度为

KX=k+jωc

(6)

式中：KX为系统的等效复刚度；k和c分别为系统的线刚度和阻尼系数；ω为系统的固有频率； j为虚数单位。

主气室内气体压强变化率为

(7)

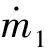
附气室内气体压强变化率为

(8)

节流孔处气体质量流量为

(9)

式中：S1，S2，S3分为弹性垫板单元工作在某一时刻时主气室、附气室、节流孔处截面积大小；g为重力加速度；H1和H2分别为主气室和附气室截面处的水平高度；ρ1为主气室内气体密度。

由式(6)～式(9)可得弹性垫板单元的等效刚度和等效阻尼系数分别为

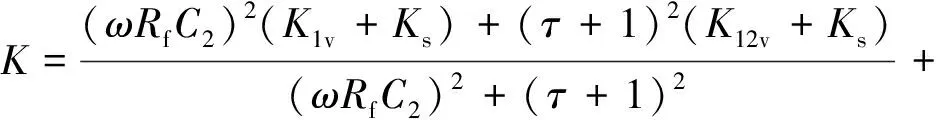
(10)

(11)

其中，

(12)

(13)

式中：Rf为节流孔阻力系数；τ为附气室与主气室体积之比，本文简称为气室体积比；P1和P2分别为弹性垫板单元工作在某一时刻时主气室和附气室的压强；K1v为弹性垫板单元主气室内气体的体积刚度；K12v为弹性垫板单元主气室和附气室体积之和的体积刚度；Ks为表面积刚度；C2为弹性垫板单元附气室气容大小；Kf和Kv分别为弹性垫板单元的库仑摩擦模型和分数K-V模型的动刚度；φf为摩擦模型的滞后角。

由于阻尼比与阻尼系数的关系呈正比， 因此空气阻尼网孔式弹性垫板单元的阻尼比可表示为

(14)

由式(10)～式(12)可见，空气阻尼网孔式弹性垫板单元的等效刚度和等效阻尼比主要与Rf和τ有关，故空气阻尼网孔式弹性垫板单元的节流孔孔径、气室体积比是影响其刚度和阻尼的主要几何参数。

2.2 节流孔孔径的影响

采用1.1节～1.3节所述的空气阻尼网孔式弹性垫板单元流固耦合有限元模型，在材料和其他结构参数不变的情况下，对于30 mm的道床用网孔式弹性垫板，要将其垂向位移控制在3 mm左右，故对弹性垫板单元上表面施加3～4 kN的均布循环正弦荷载，即Fm=1 kN，荷载频率为5 Hz，加载时间为20 s，下表面采用固定约束。图6是节流孔孔径分别为D=0.1 mm，D=0.5 mm，D=5.0 mm时空气阻尼网孔式弹性垫板单元的动刚度对比图。

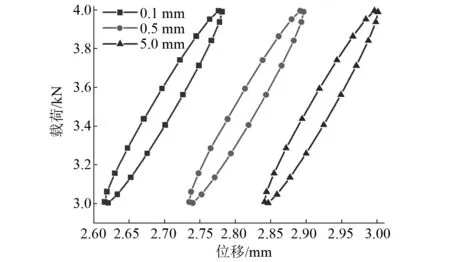
图6 不同孔径条件下动刚度对比曲线Fig.6 Dynamic stiffness comparison curve under different aperture conditions

由图6可见，在三种不同节流孔孔径对应的荷载-位移曲线在沿横轴方向出现偏移，但其形状无明显变化。三种不同节流孔孔径条件下对应的弹性垫板单元的xm依次为0.165 mm，0.162 mm，0.160 mm。故由式(1)可知，三种不同节流孔孔径条件下对应的动刚度值依次为6.034 kN/mm，6.192 kN/mm，6.250 kN/mm，所以，空气阻尼网孔式弹性垫板单元的动刚度随着节流孔孔径的减小而减小。对于一个300 mm×300 mm的道床垫，由式(2)可知其刚度依次为457.14 kN/mm，469.11 kN/mm，473.50 kN/mm。

在对空气阻尼网孔式弹性垫板进行阻尼比特性研究时，暂无特定的规定要求道床用网孔式弹性垫板的冲击载荷为多大，根据扣件用弹性垫板的疲劳试验载荷为5～35 kN，而道床用弹性垫板的有效面积比扣件用弹性垫板的大，为了更加明显的显现出道床用弹性垫板的吸能特性，故将道床用弹性垫板落锤冲击试验的冲击载荷定为75 kN，根据面积等效原则可以得到，空气阻尼网孔式弹性垫板单元上施加的冲击载荷为75/75.76≈1 kN。采用有限元软件模拟冲击载荷为1 kN的落锤试验，得到节流孔孔径分别为0.1 mm，0.5 mm， 5.0 mm条件下空气阻尼网孔式弹性垫板单元的振动衰减规律，如图7所示。图7表明，D=0.1 mm对应的初始振动幅值较大，经过若干衰减周期后，D=0.1 mm比D=5.0 mm的峰值明显减小。说明其减振效果更好。

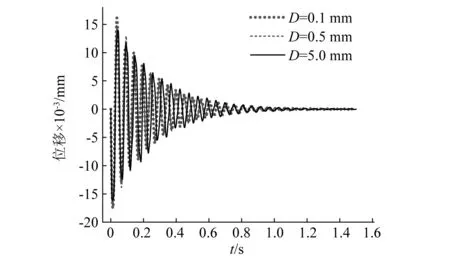
图7 不同孔径条件下自由振动衰减曲线Fig.7 Free vibration attenuation curve under different aperture conditions

选择图7中波峰趋于稳定的第2个和第8个波峰值进行阻尼比的计算。根据式(4)、式(5)可得不同节流孔孔径条件下的阻尼比大小，结果如表1所示。

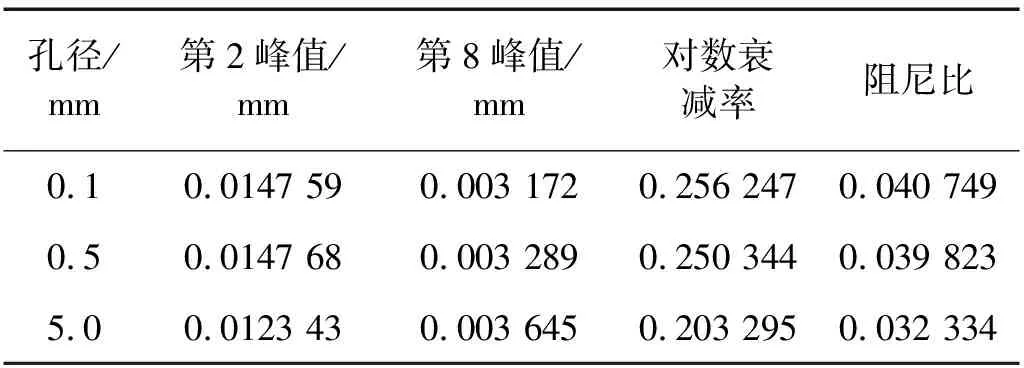
表1 不同孔径条件下空气阻尼网孔弹性垫板单元阻尼参数对比Tab.1 Comparison of damping parameters of air damping mesh elastic backing plate element under different aperture conditions

由表1可知，随着节流孔孔径的减小，空气阻尼网孔式弹性垫板单元的阻尼比随之增大，通过对比计算可知，D=0.1 mm时的阻尼比相对于D=5.0 mm时提高了26.03%。由式(3)可知，节流孔孔径对弹性垫整板的阻尼比也具有相同的影响。

2.3 气室体积比的影响

在材料和其他结构参数不变的情况下，加载和设置方式与2.2节相同。图8是气室体积比分别为0.29，0.41，0.53时空气阻尼网孔式弹性垫板单元的动刚度对比图。

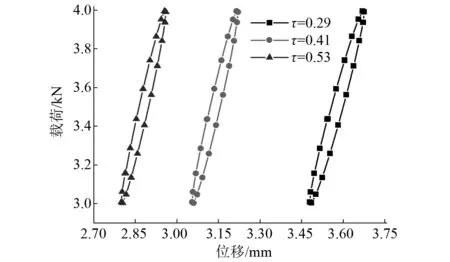
图8 不同气室体积比条件下动刚度对比曲线 Fig.8 Dynamic stiffness comparison curve under different air chamber volume ratio conditions

由图8可知，三种不同气室体积比对应的荷载-位移曲线在沿横轴方向出现较为明显的偏移，但其形状未发生变化。三种不同气室体积比条件下对应的弹性垫板单元的xm依次为0.197 mm，0.165 mm，0.161 mm。由式(1)可知，随着气室体积比的不断增大，所对应的动刚度值依次为5.086 kN/mm，6.058 kN/mm，6.228 kN/mm，所以，空气阻尼网孔式弹性垫板的动刚度随着气室体积比的增大而增大。对于一个300 mm×300 mm的道床垫，由式(2)可知其刚度依次为385.31 kN/mm，458.95 kN/mm，471.83 kN/mm。

采用2.3节相同的有限元模型模拟落锤试验，得到不同气室体积比条件下空气阻尼网孔式弹性垫板单元的自由振动衰减规律，如图9所示。图9表明，气室体积比对弹性垫板单元的振动衰减影响较为明显，气室体积比越小，所对应的自由振动衰减速度越快。

图9 不同气室体积比条件下自由振动衰减曲线Fig.9 Free vibration attenuation curve under different air chamber volume ratio conditions

选择图9中波峰趋于稳定的第2个和第8个波峰值进行阻尼比的计算。根据式(4)、式(5)可得不同节流孔孔径条件下的阻尼比大小，结果如表2所示。

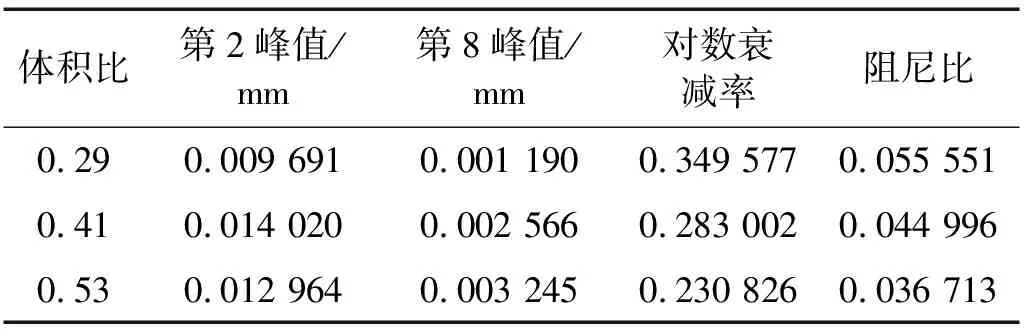
表2 不同体积比条件下空气阻尼网孔式弹性垫板单元阻尼参数对比Tab.2 Comparison of damping parameters of air damping mesh elastic backing plate element under different volume ratio conditions

由表2可知，随着气室体积比的增大，空气阻尼网孔式弹性垫板单元的阻尼比随之减小，通过对比计算可知，τ=0.53时的阻尼比相对于τ=0.29时减小了51.32%。根据式(2)可知，气室体积比对弹性垫整板的阻尼比也具有相同的影响。

3 与普通网孔式弹性垫板的对比

在以往弹性垫板的仿真计算中，并未考虑弹性垫板网孔空腔内空气对其动力学特性的影响，由2.2节和2.3节的研究可知，空气对弹性垫板动力学特性的影响是不可忽视的。因此采用与2.2节和2.3节相同的有限元计算方法研究空气对普通网孔式弹性垫板的影响，并与空气阻尼网孔式弹性垫板进行对比。

3.1 普通网孔式弹性垫板中空气的影响

以普通网孔式弹性垫板的一个网孔单元为研究对象。为了保证计算的准确性，选择同一个普通网孔式弹性垫板单元的有限元模型在有、无空气条件下进行仿真计算，两种情况下弹性垫板的应力分布云图，如图10所示。在不考虑空气作用的条件下，网孔内部最大应力值为5.153 MPa；在考虑空气作用的条件下，网孔内部最大应力值为4.912 MPa。对于普通网孔式弹性垫板单元，其内部应力分布均匀，无明显应力集中现象。

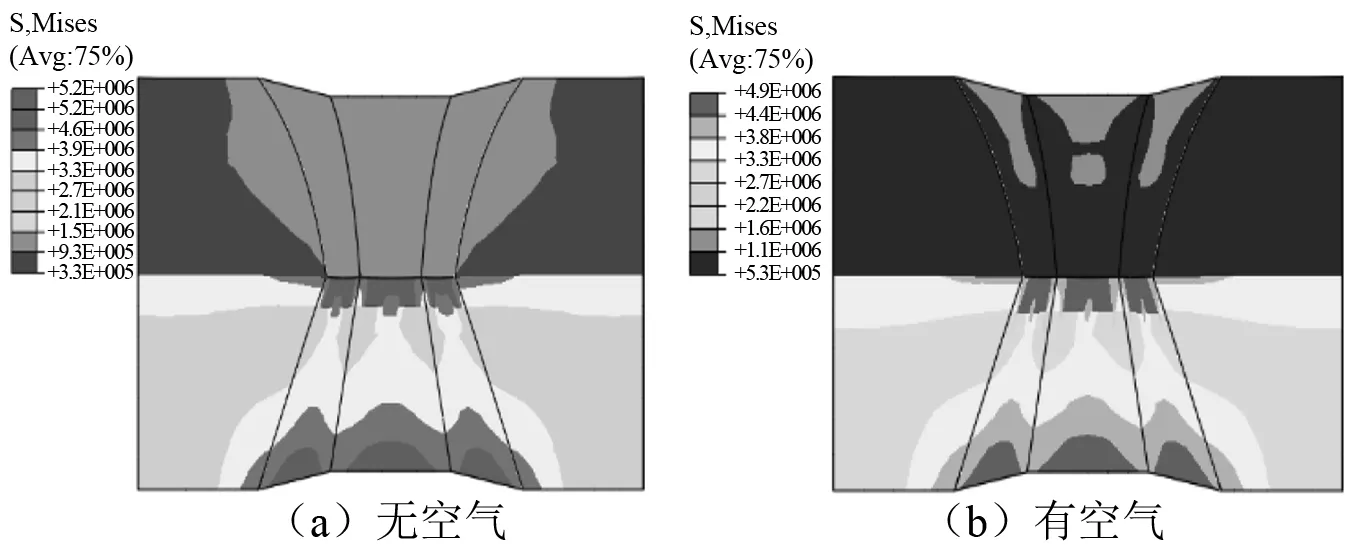
图10 两种工况下普通网孔式弹性垫板应力分布云图Fig.10 Stress distribution cloud diagram of ordinary mesh elastic backing plate under two working conditions

对普通网孔式弹性垫板单元进行有、无空气条件下的刚度特性研究时，加载和设置方式与2.2节相同。普通网孔式弹性垫板单元在考虑有、无空气条件下的动刚度对比曲线，如图11所示。由图11可见，由于弹性垫板空腔内部空气的作用，会使弹性垫板单元垂向位移压缩量减小，从而导致动刚度的曲线相比于无空气条件下整体向左略微偏移，但普通网孔式弹性垫板单元的动刚度趋势基本一致。

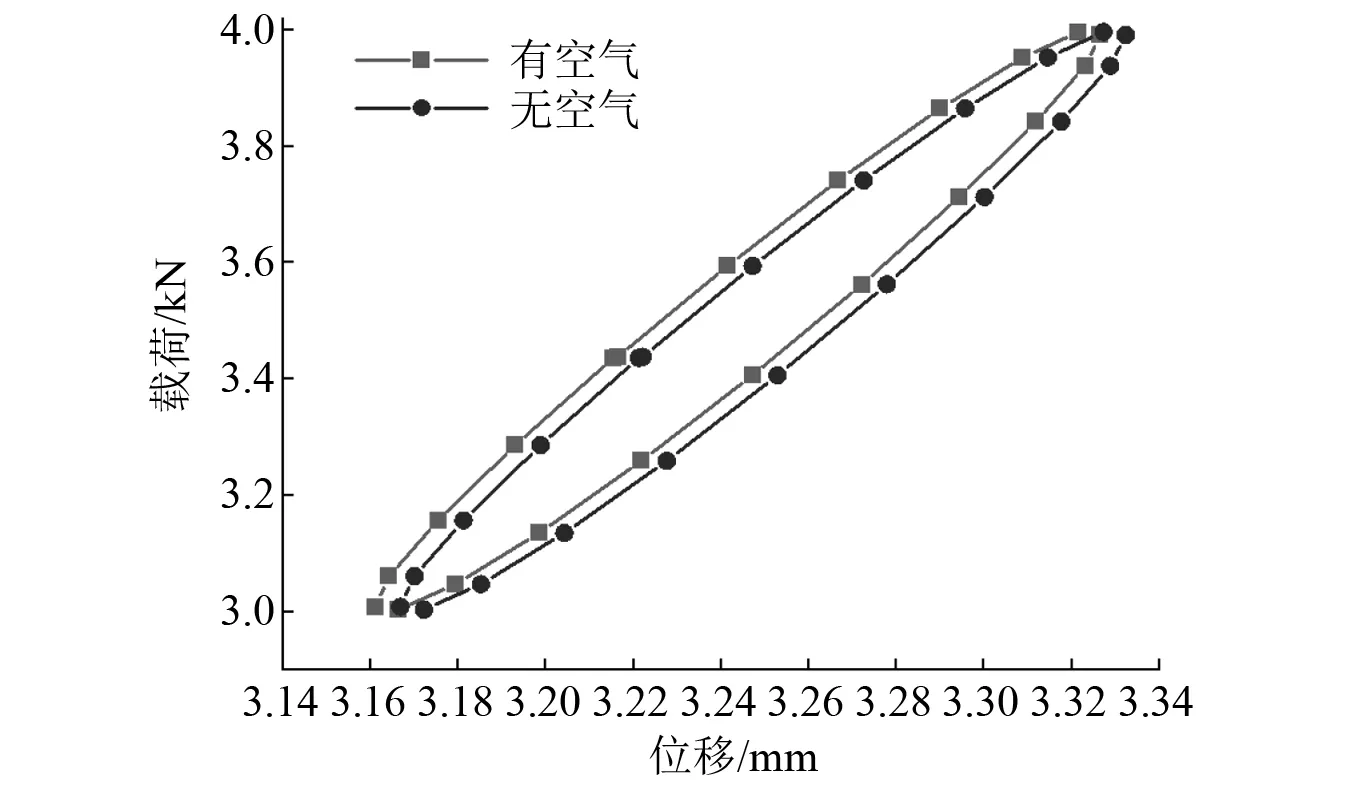
图11 普通网孔式弹性垫板有无空气条件下动刚度曲线对比Fig.11 Comparison of dynamic stiffness curves of ordinary mesh elastic pads with and without air

由图11可知，有、无空气的条件下对应的弹性垫板单元的xm依次为0.165 mm，0.168 mm，由式(1)可得有、无空气的条件对应弹性垫板单元的动刚度值依次为6.041 kN/mm，5.970 kN/mm，考虑空气后增大了1.19%。所以，空气对普通网孔式弹性垫板整板动刚度值影响较小。

模拟冲击载荷为1 kN的落锤试验，得到有、无空气条件下普通网孔式弹性垫板单元的自由振动衰减规律，如图12所示。图12表明，在考虑空气作用的条件下，弹性垫板单元对应响应的幅值略小，故空气对弹性垫板单元的自由振动衰减是有一定影响的。

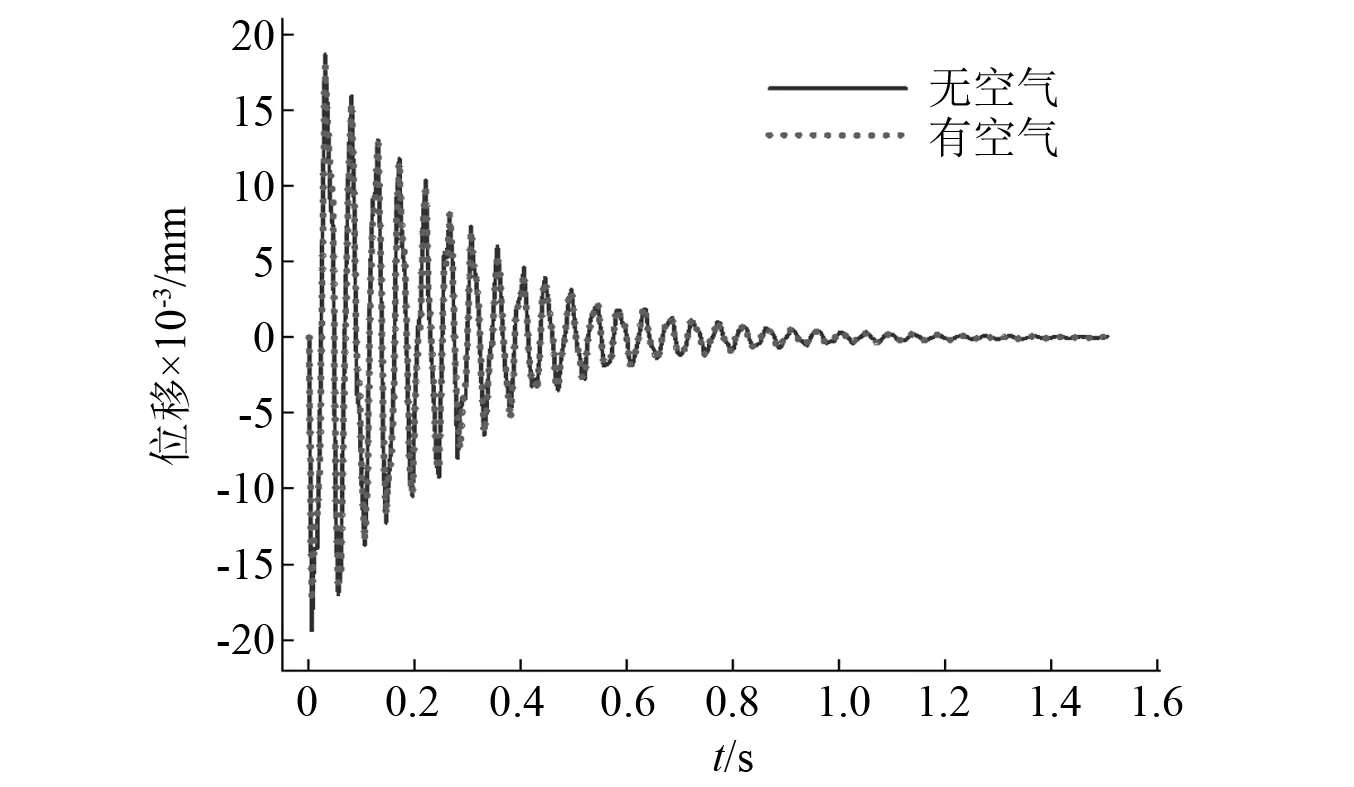
图12 普通网孔弹性垫板有无空气条件下自由振动衰减曲线对比Fig.12 Comparison of free vibration attenuation curves of ordinary mesh elastic backing plate with and without air

选择图12中波峰趋于稳定的第2个和第8个波峰值进行阻尼比的计算，波峰间隔周期数k=6。根据式(4)可得有、无空气条件下的阻尼比大小，结果如表3所示。

表3 普通网孔式弹性垫板有无空气条件下阻尼参数对比Tab.3 Comparison of damping parameters of ordinary mesh elastic pads with or without air

由表3可知，在考虑空气作用的条件下，普通网孔式弹性垫板单元的阻尼比略大，根据式(2)可知，弹性垫板整板的阻尼比相对于不考虑空气的条件下增大了6.61%。所以，在弹性垫板的动力学特性仿真计算时考虑空气是必要的。

3.2 刚度对比

在两种弹性垫板单元的材料和整体尺寸参数相同的情况下，选择D=0.5 mm，τ=0.53和D=0.1 mm，τ=0.29两种工况的空气阻尼网孔式弹性垫板与普通网孔式弹性垫板进行对比，加载和设置方式与2.2节相同。图13为三种弹性垫板单元的动刚度对比曲线。

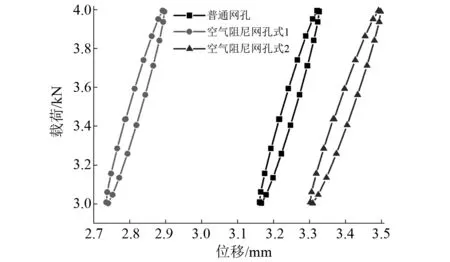
图13 三种弹性垫板单元动刚度对比曲线Fig.13 Comparison curve of dynamic stiffness of three kinds of elastic pad units

由图13可知，三种弹性垫板单元对应的荷载-位移曲线在沿横轴方向出现明显偏移。由3.1节可知，普通网孔式弹性垫板单元动刚度值为6.041 kN/mm。而两种空气阻尼网孔式弹性垫板单元对应的xm依次为0.162 mm，0.196 mm，根据式(1)可知，两种空气阻尼网孔式弹性垫板单元的动刚度值分别为6.192 kN/mm，5.106 kN/mm，D=0.5 mm，τ=0.53对应的空气阻尼网孔式弹性垫板相比普通网孔式弹性垫板动刚度值增大了2.50%；D=0.1 mm，τ=0.29工况下的则减小了15.48%。可见，空气阻尼网孔式弹性垫板的D，τ对垫板的刚度影响显著，可通过改变其取值对垫板的刚度进行调节。

3.3 阻尼对比

采用与2.2节相同的落锤试验模拟方法，得到三种弹性垫板单元在考虑空气条件下的振动衰减响应，如图14所示。图14表明，D=0.1 mm，τ=0.29工况的空气阻尼网孔式弹性垫板单元衰减速度最快，普通网孔式弹性垫板单元的衰减速度最慢。说明节流孔孔径和气室体积比越小，空气阻尼网孔式弹性垫板单元的振动衰减速度越快，减振效果更好。

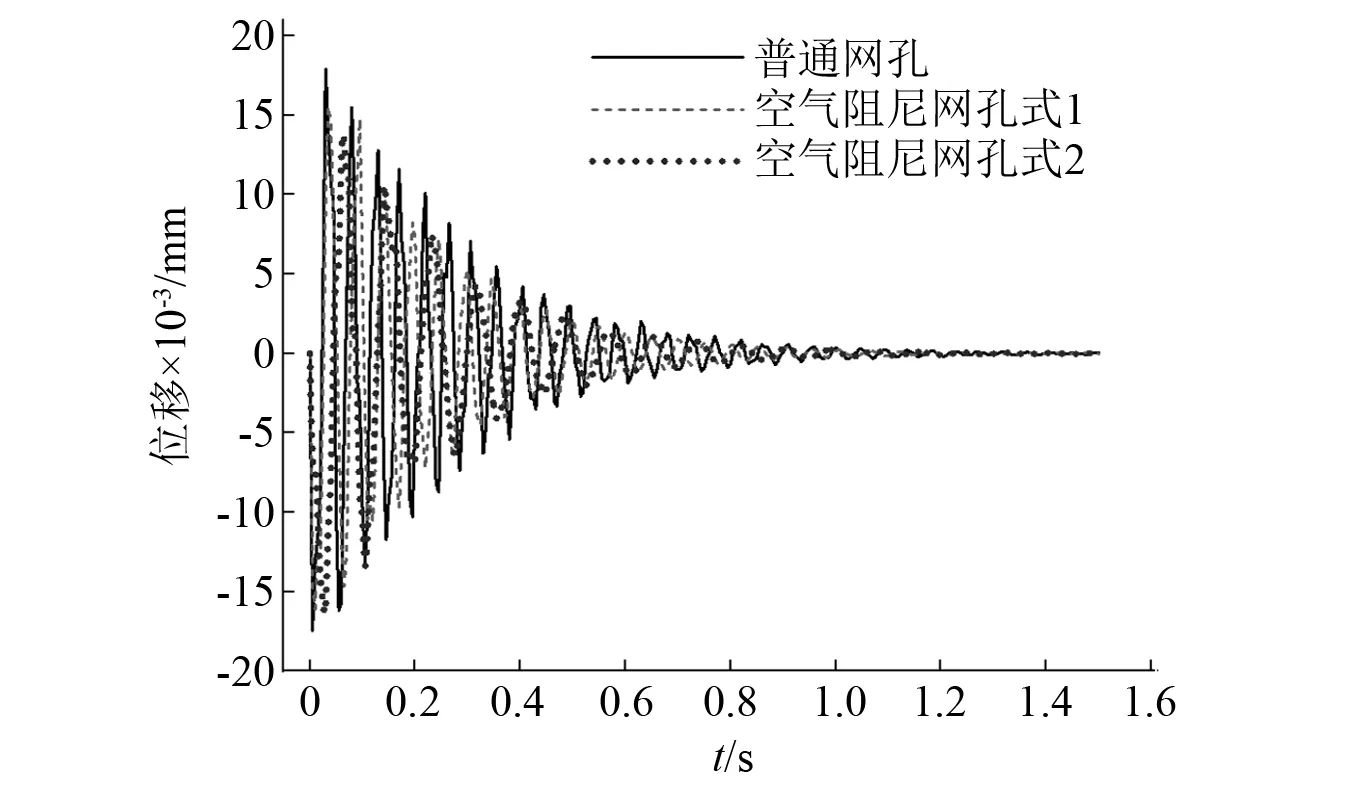
图14 三种弹性垫板单元自由振动衰减曲线对比Fig.14 Comparison of the free vibration attenuation curves of three kinds of elastic pad units

选择图14中波峰趋于稳定的第2个和第8个波峰值进行阻尼比的计算，波峰间隔周期数k=6。根据式(4)可得三种弹性垫板单元在考虑空气条件下的阻尼比大小，结果如表4所示。

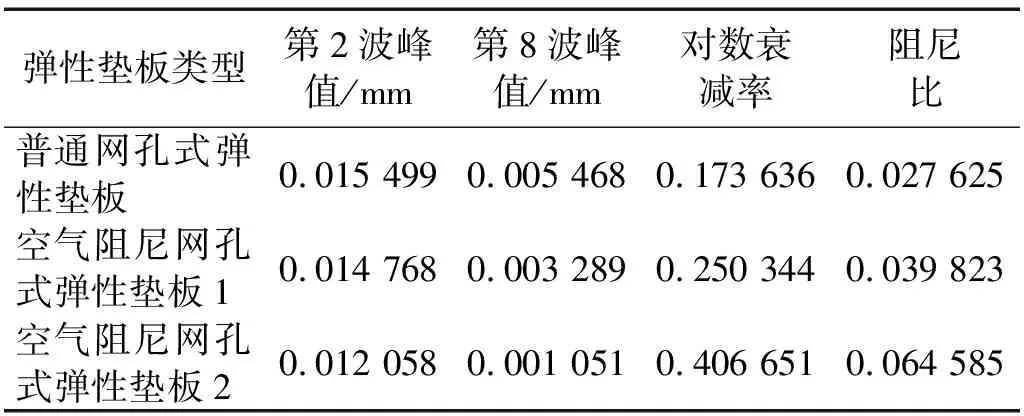
表4 三种弹性垫板单元阻尼参数对比Tab.4 Comparison of damping parameters of three elastic pad units

由表4可知，在考虑弹性垫板空腔内部空气作用的条件下，三种弹性垫板的阻尼比存在较为明显的差异，根据式(2)可知，D=0.5 mm，τ=0.53和D=0.1 mm，τ=0.29两种工况对应空气阻尼网孔式弹性垫板的阻尼比相对与普通网孔式弹性垫板整板分别提高了44.16%和133.7%。可见，空气阻尼网孔式弹性垫板D，τ对垫板阻尼的影响还要大于对刚度的影响。

4 与填充高阻尼材料的网孔式弹性垫板的对比

以普通网孔式弹性垫板单元为本体，将与其网孔内部尺寸相匹配的高阻尼填充物填充于网孔空腔内，可以进一步提高弹性垫板的阻尼。本节对比分析填充材料和利用空气两种提高阻尼的措施对垫板特性的影响规律。

4.1 应力对比

保证填充高阻尼材料网孔式弹性垫板单元的材料和整体尺寸参数与3.2节空气阻尼网孔式弹性垫板单元一致，采用Mooney-Rivlin超弹性本构模型模拟阻尼块的材料特性，本文选择单轴拉伸和双轴拉伸试验数据[21]，如表5所示。加载和设置方式与2.1节相同。考虑空气作用的条件下，空气阻尼网孔式弹性垫板的应力分布云图和空气块的速度云图，如图15所示。对于空气阻尼网孔式弹性垫板单元，根据其结构特点可知该垫板在工作状态时的形变主要在强变形层产生，所以在两者的接合面处存在应力集中的现象，但在其网孔内部应力分布均匀，其对应的最大应力值为5.894 MPa。

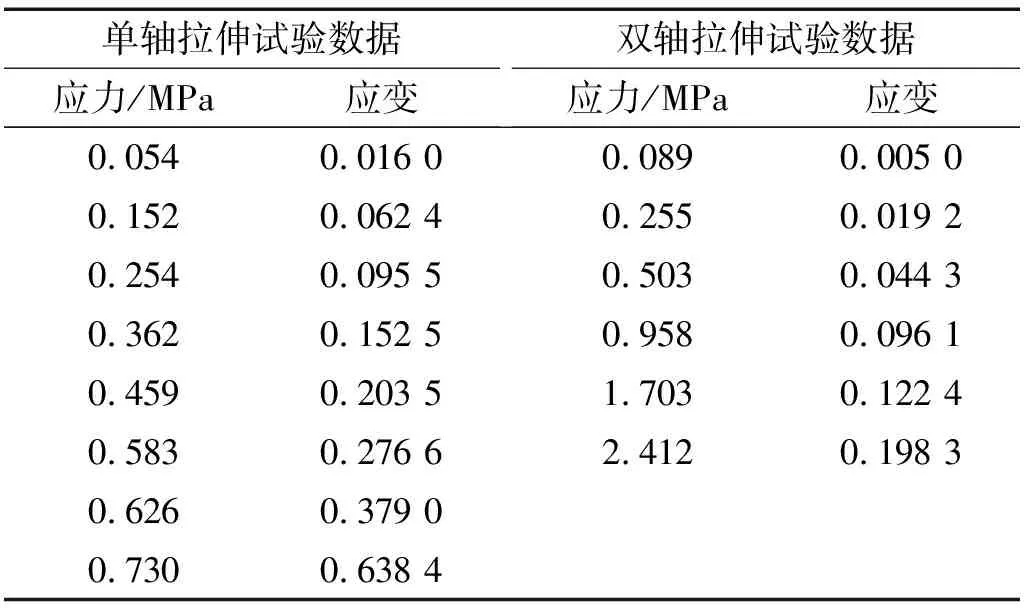
表5 单轴拉伸和双轴拉伸试验数据Tab.5 Uniaxial tensile and biaxial tensile test data

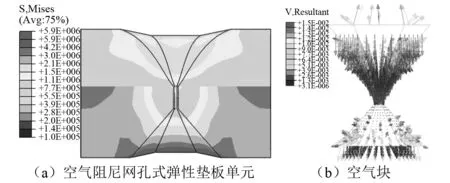
图15 弹性垫板单元应力分布云图和空气块速度云图Fig.15 Stress distribution cloud diagram and air block velocity cloud diagram of elastic pad unit

填充高阻尼材料网孔式弹性垫板单元结构和阻尼块应力云图，如图16所示。对于填充高阻尼材料的网孔式弹性垫板单元，其网孔内部应力分布均匀，无明显应力集中现象，最大应力值为0.433 MPa，阻尼块最大应力值为0.274 MPa。由于阻尼块的作用，该弹性垫板单元的最大应力值均小于前两种弹性垫板单元。可见，填充高阻尼材料对降低网孔式弹性垫板的应力具有明显的作用。

图16 弹性垫板单元和阻尼块应力分布云图Fig.16 Stress distribution cloud diagram of elastic pad element and damping block

4.2 刚度对比

对填充高阻尼材料网孔式弹性垫板单元进行动刚度特性研究时，加载和设置方式与2.2节相同。三种弹性垫板单元的动刚度对比曲线，如图17所示。

图17 三种弹性垫板单元动刚度对比曲线Fig.17 Comparison curve of dynamic stiffness of three kinds of elastic pad units

由图17可知，三种弹性垫板单元的动刚度曲线存在明显的差异，填充高阻尼材料网孔式弹性垫板单元对应的xm为0.103 mm，由式(1)可知填充高阻尼材料网孔式弹性垫板单元对应的动刚度值为9.680 kN/mm，由3.2节可知，两种空气阻尼网孔式弹性垫板单元的动刚度值分别为6.192 kN/mm，5.106 kN/mm。填充高阻尼材料网孔式弹性垫板相比两种空气阻尼网孔式弹性垫板动刚度值分别增大了56.33%和89.58%。与3.2节的结论对比可以看出，填充高阻尼材料对网孔式弹性垫板的刚度影响远大于空气阻尼的影响。

4.3 阻尼对比

采用4.2节相同的有限元模型模拟落锤试验，得到三种弹性垫板单元在考虑空气条件下的振动衰减规律，如图18所示。图18表明，填充高阻尼材料网孔式弹性垫板单元振动响应初始幅值较大，但其振动衰减速度很快，说明其具有较好的振动衰减能力；而空气阻尼网孔式弹性垫板单元的振动响应初始幅值较小，在其振动衰减到第8个波峰以后，其波峰值比填充高阻尼材料网孔式弹性垫板单元的更小，说明其振动衰减速度也很快。

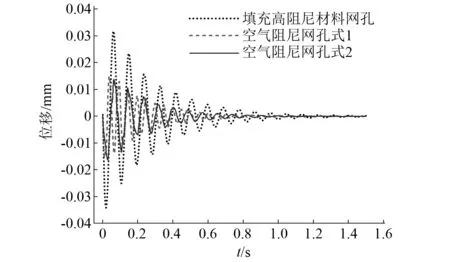
图18 三种弹性垫板单元自由振动衰减曲线对比Fig.18 Comparison of free vibration attenuation curves of three types of elastic pad units

选择图18中波峰趋于稳定的第2个和第8个波峰值进行阻尼比的计算，波峰间隔周期数k=6。根据式(4)可得三种弹性垫板单元在考虑空气条件下的阻尼比大小，结果如表6所示。

表6 三种弹性垫板单元阻尼参数对比Tab.6 Comparison of damping parameters of three elastic pad units

由表4、表6可知，三种弹性垫板的阻尼比存在明显的差异，根据式(3)可知，填充高阻尼材料网孔式弹性垫板的阻尼比明显优于普通网孔式弹性垫板；填充高阻尼材料网孔式弹性垫板整板要比空气阻尼网孔式弹性垫板整板(D=0.5 mm，τ=0.53)的阻尼比高13.17%；空气阻尼网孔式弹性垫板整板(D=0.1 mm，τ=0.29)要比填充高阻尼材料的网孔式弹性垫板整板的阻尼比高23.14%，即相对于空气阻尼网孔式弹性垫板，可通过改变其节流孔孔径和气室体积比提高其阻尼性能，得到阻尼特性更优于填充高阻尼材料的网孔式弹性垫板。

5 结 论

(1) 节流孔孔径和气室体积比对空气阻尼网孔式弹性垫板的动刚度和阻尼比都有一定的影响。随着节流孔孔径的减小，弹性垫板的动刚度随之减小，而阻尼的变化趋势与刚度相反；随着气室体积比的增大，弹性垫板的动刚度的随之增大；而阻尼比随之减小。

(2) 对于普通网孔式弹性垫板，在考虑弹性垫板空腔内部空气作用的情况下，其动刚度和阻尼相对于不考虑空气条件下的分别增大了1.19%和6.61%。由于对阻尼的影响较大，所以在弹性垫板的动力学特性仿真计算时考虑空气是必要的。

(3) 与普通网孔式弹性垫板对比，空气阻尼网孔式弹性垫板可通过改变节流孔孔径和气室体积比，得到刚度和阻尼特性均优于普通网孔式弹性垫板的工况。空气阻尼网孔式弹性垫板节流孔孔径、气室体积比对垫板阻尼的影响比刚度更明显。

(4) 填充高阻尼材料虽然可以进一步提高网孔式弹性垫板的阻尼比，但其阻尼比调高能力不及空气阻尼网孔式弹性垫板，且阻尼块造价成本高也不易填充于网孔空腔内；空气阻尼网孔式弹性垫板具有较小的刚度和较大的阻尼，且可通过改变节流孔孔径和气室体积比灵活调整阻尼，故空气阻尼网孔式弹性垫板具有更好的减振性能。