一类组合群论问题
田开宇, 王慧群, 夏利猛
(1. 江苏大学 数学科学学院, 江苏 镇江 212013; 2. 长治学院 数学系, 山西 长治 046011)
0 引 言
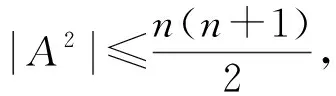

基于上述研究, 本文主要给出B(6,22),B(6,23),B(6,24),B(7,29),B(7,30),B(8,37)群的刻画.除使用GAP(groups, algorithms, programming)[17]软件计算外, 本文还刻画了上述B(n,k)群, 并部分指出了B(n+1,n+k)群与B(n,k)群之间的一般联系, 从而推广了文献[16]的结果.若无特别说明, 本文所有的群G均为非平凡B(n,k)群.
1 预备知识
引理1设G是有限群, 且|G|>n(n+k).如果G是B(n+1,n+k)群, 则G是B(n,k)群.
证明: 反证法.假设G不是B(n,k)群, 即存在G的一个n元子集B={b1,b2,…,bn}, 使得|B2|>k.由于G是B(n+1,n+k)群, 故|B2|≤n+k.令
Bl={x∈G|xB∩B2≠Ø}.

由于|G|>n(n+k)≥|Bl|, 故有G-Bl≠Ø, 即存在u∈G,u∉Bl, 使得uB∩B2=Ø.
令A=B∪{u}, 则A2=B2∪uB∪Bu∪{u2}.所以
|A2|=|B2∪uB∪Bu∪{u2}|≥|B2∪uB|=|B2|+|uB|>n+k,
与|A2|≤n+k矛盾.故结论成立.证毕.
因此, 当|G|>120时,B(6,24)群是B(5,19)群; 当|G|>180时,B(7,30)群是B(6,24)群; 当|G|>259时,B(8,37)群是B(7,30)群.
引理2[12-13]设G为非平凡B(5,19)群, 则其必满足下列条件之一:
1)G为Abel群.
2) 若G为2群, 则G≅Q8×E2, 其中E2是初等交换2群, 且|E2|≥4.
3) 若G为非2群, 则G为下列群之一:



④C3×Q8.
2 主要结果
定理1设G为非平凡的B(6,24)群, 则G为Abel群.
证明: 当|G|>120时, 由引理1, 可以考虑B(5,19)群.由引理2, 需说明Q8与初等交换2群的直积不是B(6,24)群.
先证明G=Q8×C2×C2不是B(6,24)群.记
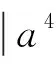
则G=Q8×〈z1〉 ×〈z2〉.再取
A={a,b,ab,az1,bz2,abz1z2},
通过直接计算可得|A2|=28>24, 故Q8×C2×C2不是B(6,24)群.
对于初等交换2群E2, 当|E2|≥4时,Q8×C2×C2是Q8×E2的一个子群, 所以Q8×E2(其中|E2|≥4)不是B(6,24)群.因此当|G|>120时,G为Abel群.
对于阶数不超过120的非平凡B(6,24)群, 用GAP验证都是Abel群.证毕.
由定理1, 可进一步得到B(6,23)群和B(6,22)群的结构.
推论1设G为非平凡的B(6,23)群, 则其必满足下列条件之一:
1)G为Abel群;




推论2设G为非平凡B(6,22)群, 则G为Abel群.
定理2设G为非平凡B(7,30)群, 则G或者是Abel群, 或者同构于Q8×C2×C2.
证明: 由定理1和引理1可知, 当|G|>180时,G为Abel群. 再使用GAP验证31~180阶群, 可得结论.证毕.
推论3设G为非平凡B(7,29)群, 则G为Abel群.
证明: 由于B(7,29)群总是B(7,30)群, 由定理2只需验证30阶非交换群和Q8×C2×C2.通过GAP计算可知, 30阶的非交换群共有3个:
1)C5×S3=〈a,b,c|a5=b3=c2=1,cb=b2c, [a,b]=[a,c]=1〉;
2)C3×D10=〈a,b,c|a5=b3=c2=1,ca=a4c, [a,b]=[b,c]=1〉;
3)D30=〈a,b|a15=b2=1,ba=a14b〉.
对上述3个群分别取7元子集:
A={b,c,ab,ac,a2b,a2bc,a4b2c},A={a,c,ab,ac,bc,a2,a4b2c},A={a,b,ab,a2,a2b,a6,a6b},
均有|A2|=30; 对Q8×C2×C2, 取7元子集A={a,b,ab,ac,bd,abcd,a3}, 则有|A2|=30.因此它们都不是B(7,29)群.故非平凡B(7,29)群只能是Abel群.证毕.
进一步可得B(8,37)群的刻画.
定理3设群G为非平凡B(8,37)群, 则G为Abel群.
证明: 当|G|> 259时, 由定理2和引理1可知,G为B(7,30)群; 更进一步,G为Abel群.为此只需检验38~259阶的非Abel群.记|G|=m, 使用GAP软件计算可知, 当38≤m≤259且m≠256时, 所有的非Abel群都不是B(8,37)群.为完成证明, 只需证明256阶B(8,37)群是Abel群.
下面使用反证法证明256阶B(8,37)群, 只能是Abel群.
假设G为非Abel群.先证明G的每个真子群都是Abel群.若不然, 必存在一个非Abel的真子群H 其中α≥2, |G|=2α+β; 或者 其中α≥2,α≥β, |G|=2α+β+1. 若G=G1, 则当α=2,3或4时, 令 A={a,b,ab,a3b,ab3,ab5,b2,b11}; 当α=5,6或7时, 令 A={a,b,ab,a3b,a5b,a7b,a2,a5}. 由计算可得|A2|>37.在所有情形中, 都可以找到一个8元子集A, 使得|A2|>37, 所以G1不是B(8,37)群. 若G=G2, 令c=[a,b], 则G2可表示为 G2=〈a,b,c|a2α=b2β=c2=1, [a,b]=c, [a,c]=1, [b,c]=1〉,α≥β. 当α=4,5或6时, 令A={a,b,ab,abc,a3b,a5b,a2,a9}.易算出|A2|>37, 所以G2不是B(8,37)群. 综合上述讨论可知,G1和G2都不是B(8,37)群, 与题设矛盾.因此G为Abel群.证毕.


