HPM视角下“三角形内角和定理”的教学设计

200336 上海市仙霞高级中学 许 意

HPM是指数学史在数学教学中的渗透

.

笔者通过查阅三角形内角和定理的相关资料，采用HPM视角开展教学，重组教学内容，重构教学过程，借助数学史重现数学问题发现和解决的过程，帮助学生领悟数学问题解决的一般规律

.

一、 历史材料及其运用

公元前6世纪，古希腊数学家泰勒斯通过拼图发现三角形内角和定理

.

古希腊数学家毕达哥拉斯、欧几里得采用过三角形一个顶点作对边的平行线的方法，将三个内角转化为一个平角

.

现行教材(如沪教版七下教材、苏科版七下教材、沪科版八上教材)也大多采用这样的方法

.

除添平行线法以外，法国数学家克莱罗在《几何基础》中给出了证明三角形内角和定理的另一种方法

.

德国数学家提波特首次利用旋转方法证明了三角形内角和定理

.

查阅资料后，笔者认为证明方法大致可以分为添平行线法与不添平行线法

.

平行线的添加原理大致相同，学生较易理解，可以作为学生论证的基本方法

.

不添平行线的方法较难讲解，可通过视频资源和几何画板等现代教育技术手段辅助讲解

.

本节课结合HPM的理论框架，运用附加式、顺应式这两种数学史教学方式，呈现知识形成的自然过程，帮助学生理解三角形内角和定理

.

二、 教学设计与实施

(一)三角形内角和定理的发现

问题1

三角形的三个内角有怎样的数量关系？如图1，教师边讲解边使用几何画板演示三角形内角和计算结果，使学生对三角形内角和等于180°有直观感受

.

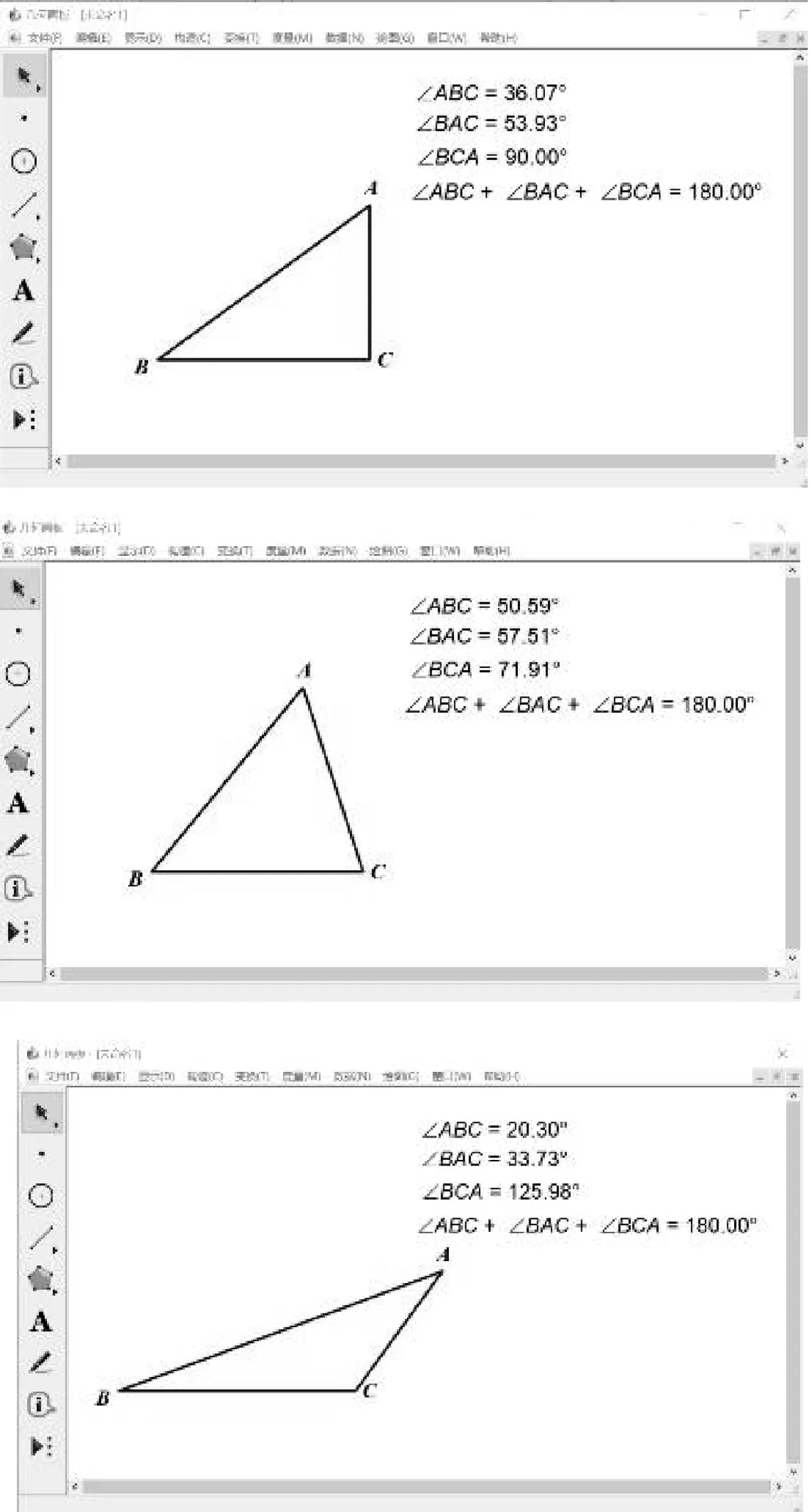
图1

设计意图：

在小学阶段，学生已认识三角形，并了解三角形内角和为180°

.

通过几何画板的操作演示，学生直观感受到随着三角形形状的改变，三角形三个内角的大小也会改变，不变的是三个内角和始终为180°

.

演示过程符合该阶段平面几何学习以实验几何为主的学习方式

.

相传，公元前6世纪，古希腊数学家泰勒斯在观察工人装修的过程中，通过观察瓷砖的铺设，发现了三角形内角和为180°

.

教师边讲述泰勒斯的故事，边播放小视频(视频来源网站：哔哩哔哩，网址：https://www.bilibili.com/video/BV1j64y1Z7xk，图2显示了视频的某一片刻)

.

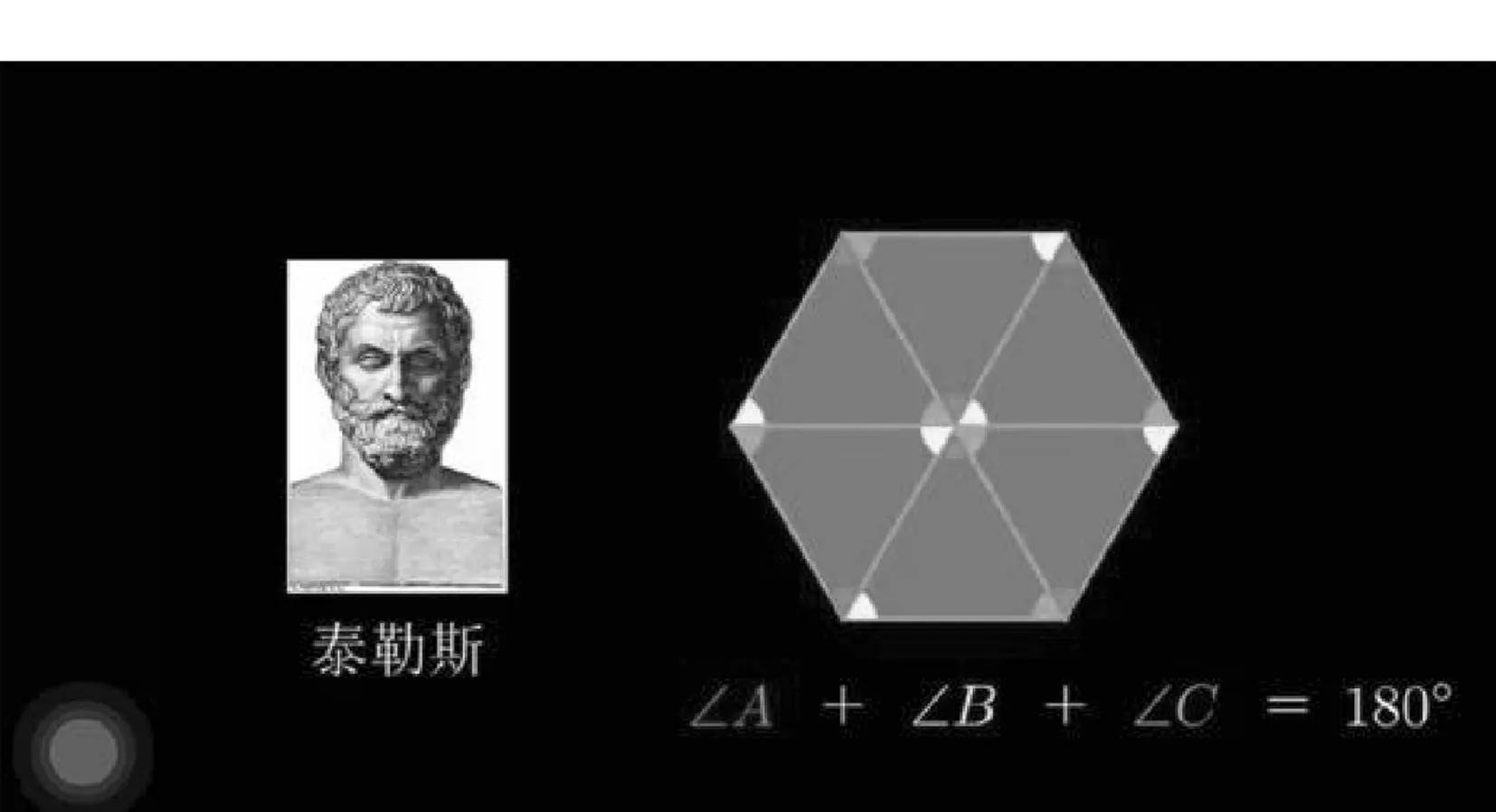
图2

设计意图：

有资料显示，泰勒斯通过拼图发现三角形内角和定理

.

为使学生直观感受泰勒斯的证明方法，笔者选用视频资料演示证明过程

.

问题2中的证明采用实验论证的方法

.

该种证明方式还可以讨论将六个同样大小的等边三角形转化为六个同样大小的等腰三角形，或者将其替换成不等边三角形来拼图的情况

.

泰勒斯的证明方法不作为重点，可以启发学生课后思考与研究

.

泰勒斯是西方思想史上第一位有记载有名字留下来的思想家，他曾利用日影测量金字塔的高度，泰勒斯定理以他命名……在视频网站中，可以找到泰勒斯在数学方面划时代贡献的相关介绍，且有些视频以动画形式呈现，在课堂上播放小视频使数学史不再只是书本上的文字，真正实现搭建数学与人文、数学教学与学生探究的桥梁

.

(二)三角形内角和定理的证明

活动1

历史上有多位数学家对三角形内角和为180°进行了研究

.

1809年，德国数学家提波特通过旋转法证明了三角形的内角和为180°

.

教师通过视频(图3显示了视频的某一片刻)，演示旋转法的证明过程：固定笔的中心，顺时针或逆时针依次转动图中∠1、∠2和∠3的相应度数

.

观察三次转动后笔尖的方向，即可发现三角形内角和为180°

.

图3

设计意图：

活动1基于提波特的证明法，该法符合学生实验几何的学习经历，即通过平移、旋转、翻折等运动方式，结合生活经验和几何图形经验，直观感受几何图形的某些特性，并总结相关规律，从而引导学生对结论进行演绎推理，激发学生探究的兴趣

.

多媒体教学在现在教学中扮演着越来越重要的角色。录播系统是多媒体教学的一种。录播系统通常由以下几部分组成：高清录播主机，音视频采集系统，自动跟踪系统，白板及可触控电视。

活动2

关于三角形内角和为180°的证明，不得不提起一个人，大家对他并不陌生，他就是毕达哥拉斯

.

我们今天就来研究一下他的证明方法

.

教师介绍，学生完成证明过程:

如图4，在△

ABC

的顶点

A

作直线

EF

∥

BC

，由平行线的性质“两直线平行，内错角相等”证得

.

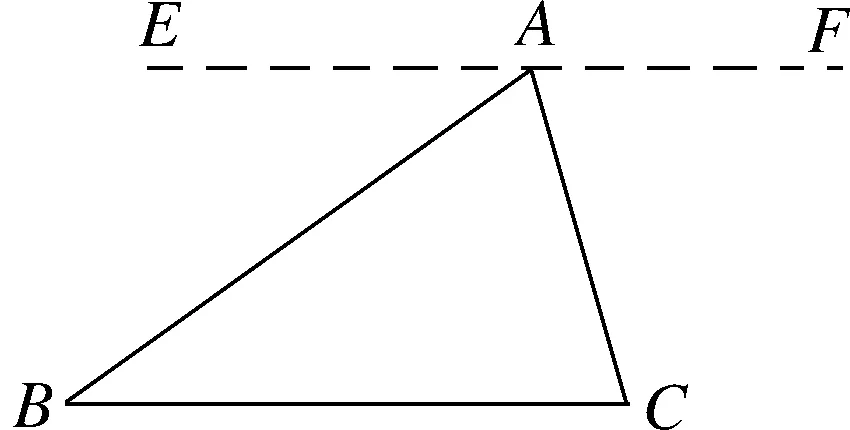
图4

∵

EF

∥

BC

(已知)，∴∠

EAB

=∠

B

,∠

FAC

=∠

C

(两直线平行，内错角相等)

.

∵∠

EAB

+∠

BAC

+∠

FAC

=180°(平角的意义),∴∠

B

+∠

BAC

+∠

C

=180°(等量代换)

.

设计意图：

泰勒斯从拼图的实践中发现了三角形内角和，这样的发现是实验性的，但他并未证明该定理

.

毕达哥拉斯学派在泰勒斯的基础上发现了更多的几何定理，如“两直线平行，内错角相等”及其逆定理

.

知道平行线的上述性质，再证明内角和定理就是水到渠成的事了

.

沪教版教材也采用了该方法进行证明

.

同时，详细讲解毕氏证明法可以帮助学生理解欧几里得、克莱罗的证明方式

.

毕达哥拉斯发现了奇数、偶数、素数、合数、完美数等，他证明了三角形内角和定理，他还发现了黄金分割

.

毕达哥拉斯在几何、代数领域的卓越成就值得学生了解和学习

.

在活动2中，学生自主完成证明过程，融入古人的发现旅程，提升对数学史研究的兴趣，感受与伟人同行的成就感

.

活动3

毕达哥拉斯证明法的再探究师：同学们，毕达哥拉斯的证明方法是过三角形的顶点作平行线，将三角形三个内角转化成平角，证得三角形内角和为180°

.

请思考，如果将过三角形一个顶点改为过三角形边上的任意一点添平行线，还能证明三角形内角和为180°吗？学生以小组为单位，讨论过三角形一边上的任意一点作平行线，口述证明过程

.

已知：如图5，点

M

为

AB

上的一点，请说明∠

A

+∠

B

+∠

C

=180°

.

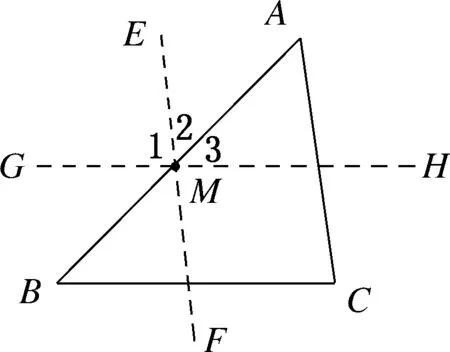
图5

过

AB

边上的一点

M

作

EF

∥

AC

,

GH

∥

BC.

∵

EF

∥

AC

，∴∠

A

=∠2，∵

GH

∥

BC

，∴∠

B

=∠

GMB.

又∵∠

GMB

=∠3，∴∠

B

=∠3

.

同理可得∠

C

=∠1

.

∵∠1+∠2+∠3=180°，∴∠

A

+∠

B

+∠

C

=180°

.

师：通过同学们的讨论，我们发现过三角形边上的任意一点作平行线，也能将三角形三个内角转化为平角，证得三角形内角和为180°

.

我们是否可以进一步将三角形三边上的任意一点改为平面内的任意一点进行证明呢？学生再次尝试，并证得结论

.

已知：如图6，点

M

为平面内的一点，请说明∠

A

+∠

B

+∠

C

=180°

.

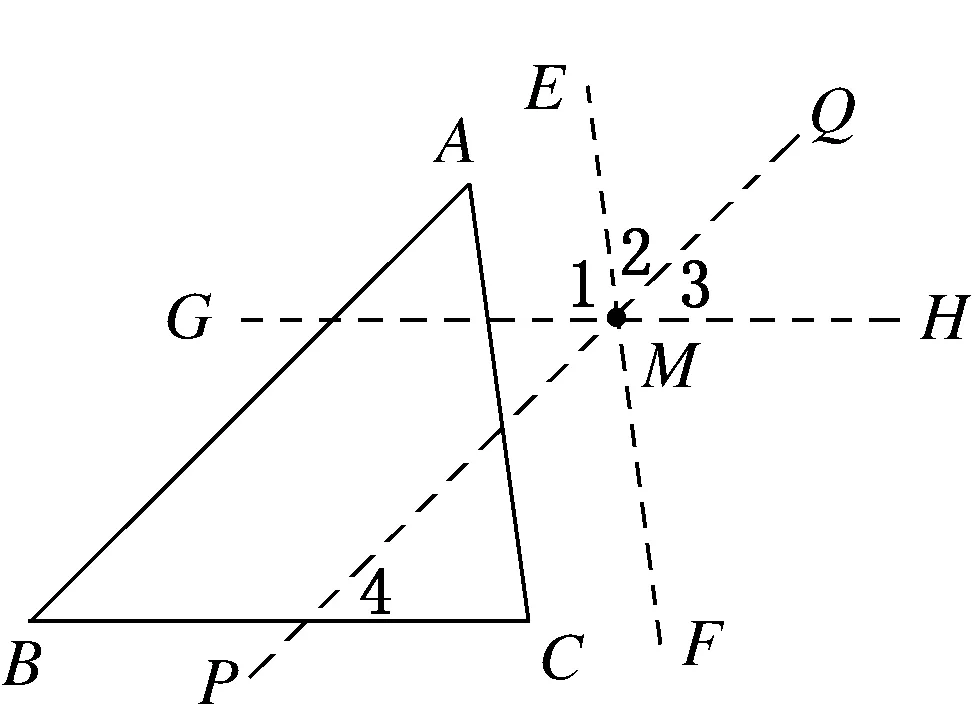
图6

过平面内任意一点

M

作

EF

∥

AC

,

GH

∥

BC

，

PQ

∥

AB.

∵

GH

∥

BC

，∴∠3=∠4，∵

PQ

∥

AB

，∴∠

B

=∠4，∴∠

B

=∠3

.

同理可得∠

C

=∠1,∠

A

=∠2

.

∵∠1+∠2+∠3=180°，∴∠

A

+∠

B

+∠

C

=180°

.

设计意图：

活动3是整节课探究的重点

.

通过对毕达哥拉斯证明方法的再探究，学生感受化归数学思想的魅力

.

毕达哥拉斯证明法的再探究使学生感受从特殊到一般的研究方法

.

从特殊到一般的研究过程符合人类认识事物的过程

.

数学学习的过程中，无论是公式还是定理，往往都是从特殊开始形成一般结论，解决其他相关问题

.

活动3中，从特殊点的添平行线法到平面内任意一点添平行线的研究，学生对三角形内角和定理产生更深层次的理解

.

活动3的设计使学生有更强的成就感

.

牛顿曾说：“我比别人看得远是因为我站在了巨人的肩膀上

.

”如果数学课堂仅停留在对历史证明方法的介绍上，这节课只能称为数学史拓展课

.

HPM视角下的数学教学强调知识产生的历史动机与学生学习的动机

.

融入数学史的数学教学意义在于教授学生如何学以及怎么学

.

通过这节课的学习，学生对古代数学问题产生浓厚的兴趣

.

从特殊到一般的证明过程也进一步激发了学生学习数学的积极性，所学即所用的方法使学生以数学独有的严谨态度研究数学问题

.

(三)三角形内角和定理的形成

教师板书三角形内角和定理，并将定理转化为数学语言

.

设计意图：

在学生认识到三角形内角和为180°后，教师自然地给出三角形内角和定理，至此学生完成了概念的建构和形成过程

.

(四)三角形内角和定理的巩固与内化

例题

在△

ABC

中，∠

B

=35°，∠

C

=55°，求∠

A

的度数，并判断△

ABC

的形状

.

练习

五边形

ABCDE

的内角和等于多少度？你能运用三角形内角和定理加以证明吗？

设计意图：

设置例题的目的是为学生进行示范，有利于学生的参与和探索，感受数学学习的完整性；有利于培养学生的语言表达能力，使学生体会数形结合的思想

.

练习题的设计建立在学生已有的认知水平及知识经验的基础上，具有一定的挑战性

.

引导学生通过联结对角线，将五边形的内角和转化为三角形内角和进行探究

.

将一个问题由难化易、由未知化已知的解题策略，旨在激发学生探究的欲望，让学生体会化归的数学思想

.

三、 教学设计立意解析

(一)HPM视角下教学内容的再整合

三角形内角和定理是平面几何中最重要的定理之一

.

教材强调实验几何中的操作部分，强调演绎推理，忽视结论发现的曲折过程，忽视数学知识产生的类比与归纳过程

.

数学本身在不断发展(不断发现问题并解决问题)的过程中得到完善

.

三角形内角和定理本身有着悠久的历史，有着众多精彩的证明方法

.

在这节课中，笔者改变思路，将数学史融入三角形内角和定理教学，与学生一同经历三角形内角和定理的发现，探究不同的论证方法以及该定理的应用，体验丰富的人文与历史底蕴

.

(二)HPM视角下教学手段的再整合

融入数学史的课堂需要学生知识体系的整合，还需要学生认知体系的整合

.

因此，现代教育技术的加入改变了传统授课模式，以动态的形式精准地表现数学知识的发生发展过程

.

例如，在对三角形三个内角的数量关系的探究中，选用几何画板度量三角形三个内角的大小，既能使学生有直观的感受，又能达到数形结合的目的

.

在介绍毕达哥拉斯生平故事时，笔者播放了网络上查找到的动画视频

.

视频的播放使学生视觉与听觉得以整合，增加书面材料的感染力，同时突破时间、空间上的局限，激发学生在课堂中的参与度与心理上的认同感

.

又如，介绍1809年德国数学家提波特提出的旋转法时，视频资源使原本晦涩难懂的证明原理变得清晰易懂，将抽象的过程以简单准确的方式呈现，帮助学生理解该种方法的简便性与可操作性

.

笔者通过对数学史资料的查阅、网络资源的查找，在三角形内角和定理教学中，借助多媒体技术将数学史与教学内容紧密结合，学生参与度高，学习的主体地位得到尊重

.

学生学习兴趣高涨、学习氛围浓厚，课堂教学效果显著

.

与数学史相结合的课堂教学对教师自身素养的要求较高，在今后的教学中，如何将隐形的历史融入显性的数学学习中，将是笔者继续努力的方向

.