研究高考真题 探究命制轨迹 提升备考效率——以一道解析几何高考真题为例

甘肃 张 科 广东 骆妃景

(作者单位：甘肃省兰州市榆中县恩玲中学 广东省东莞市麻涌中学)

往年的高考试题是精雕细磨的产物，它反映了对考试内容的深思熟虑、对设问和答案的准确拿捏、对学生水平的客观判断.研究这些试题，就如同和试题的命制者对话.解析几何真题往往具有很多优美的性质与结论，不少解析几何试题源于圆锥曲线的某几个性质，背景深远，内涵丰富，是研究的好素材，备受高中数学教师青睐.2021年高考数学全国乙卷理科第21题就是一道极具内涵的试题，从解法和背景来看，正是历经千年，无穷魅力的阿基米德三角形及其性质内蕴好题，试题如下：

【例】(2021·全国乙卷理·21)已知抛物线C：x2=2py(p>0)的焦点为F，且F与圆M：x2+(y+4)2=1上点的距离的最小值为4.

(1)求p；(2)若点P在M上，PA，PB是C的两条切线，A，B是切点，求△PAB面积的最大值.

本题以抛物线和圆这两种熟悉的几何图形为载体，考查抛物线的切线和最值问题，作为2021年高考数学全国乙卷理科压轴题，表面上看似熟题，但做起来容易产生思维“卡壳”，让学生无从下手.

第(1)问求p值，比较基础，只需对已知条件进行“翻译”，即用p表示出焦点坐标，再运用“圆外一点到圆上一点的距离”相关知识列出一元一次方程即可顺利求解.本小问虽然简单，但是求第(2)问的必经之路，若计算错误，则第(2)问必将一败涂地.

第(2)问求三角形面积的最大值，题干叙述简洁明了，但解题时不好入手.首先要选对方法，本题中几何法应当被排除，故考虑代数法，即用代数的方式表示出三角形的面积，再利用函数或不等式求出最值.该问侧重考查考生的数形结合思想、化归与转化思想以及运算求解能力，显然具有较好地选拔功能.

1.思路分析，解法探究

第(1)问解法分析

本小问主要考查“圆外一点到圆上一点的距离”问题.若设圆外一点到圆心的距离为d，圆的半径为r，则圆外一点到圆上一点的距离的最大值为d+r，最小值为d-r.灵活运用该结论，目标问题即可迎刃而解.

第(2)问解法分析

思路1：利用导数的几何意义，求出抛物线的两条切线方程，从而求出切点弦所在直线方程，然后联立方程组利用韦达定理，由弦长公式及点到直线的距离公式表示出三角形的面积，最后利用函数单调性求解.

设点A(x1，y1)，B(x2，y2)，P(x0，y0)，

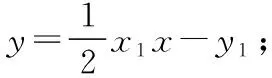
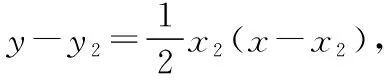
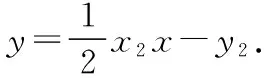
又因为点P(x0，y0)在切线PA，PB上，

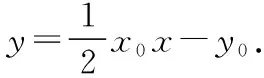
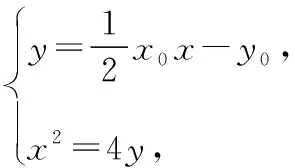
则x1+x2=2x0，x1x2=4y0.

评注：该解法是处理此类问题的常规解法，也是大部分学生求解过程中使用的最直接的方法，利用导数的几何意义求出切线方程，进而求出切点弦所在直线方程，然后联立方程组表示出三角形面积，最后转化为函数最值问题.

思路2：利用抛物线上任意一点切线方程的性质，先写出切线方程，进而求出两条切线的交点坐标，通过分析可知该交点与弦的中点横坐标相同，得到线线平行，进而表示出三角形面积，最后利用函数求解最值.

解法二：由(1)知抛物线C的方程为x2=4y.

设点A(x1，y1)，B(x2，y2)，P(x0，y0)，则由抛物线上一点的切线方程的性质可知，切线PA的方程为xx1=2(y+y1)，切线PB的方程为xx2=2(y+y2).

又由点P(x0，y0)在圆M上，

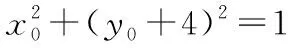
评注：该解法利用抛物线上一点的切线方程的性质，先求出两条切线方程，进而求出交点的坐标；然后结合中点坐标公式得出平行关系；最后利用“分割与组合思想”表示出三角形面积，将目标问题转化为相关函数的最值问题，进而利用函数性质求解最值.

思路3：根据直线与抛物线相切联立方程组，利用根与系数的关系、导数与斜率、方程根的思想表示出三角形面积的表达式，再运用二次函数法分析问题的最值，然后巧妙运用点在圆上，使问题转化为变量在一定范围内函数的最值问题.

解法三：由(1)知抛物线C的方程为x2=4y.

设圆上任意一点P(x0，y0)，过点P作抛物线的切线斜率为k，则切线方程为y=k(x-x0)+y0.

设两条切线PA，PB的斜率分别为k1，k2，

则有k1+k2=x0，k1k2=y0③.

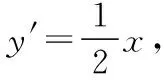
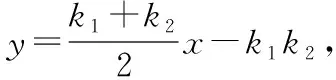
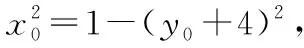
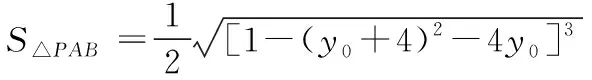
评注：采用熟知的通性通法，先将直线与抛物线相切转化为对应方程的判别式为零；然后运用根与系数的关系、化归与转化思想、方程思想分析问题；最后根据函数思想，顺利求解三角形面积的最大值.

思路4：利用导数及斜率公式切入，然后运用方程的思想转化出有关变量的表达式，进而求出三角形的面积，最后利用函数性质求出最值.

解法四：由(1)知抛物线C的方程为x2=4y.

设点A(x1，y1)，B(x2，y2)，P(x0，y0)，

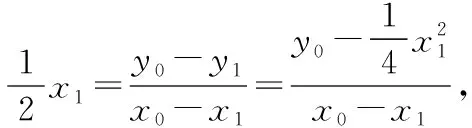
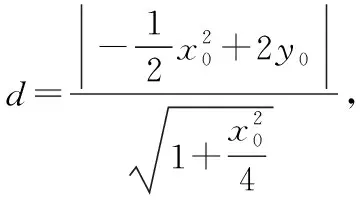
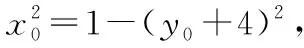
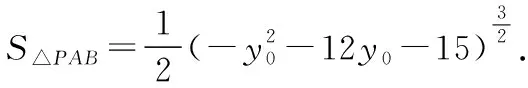
评注：该方法利用了导数和斜率公式，运用了方程思想，转化了各变量间的关系，应用弦长公式和点到直线的距离公式将三角形的面积进行了表示，最后利用函数的性质灵活求解最值问题.

思路5：借助圆的参数方程设点，利用点斜式得到抛物线的切线方程，与抛物线方程联立方程组，并令Δ=0得到动点坐标和切点坐标，从而得到直线AB的方程以及线段AB的长，再求出点P到直线AB的距离，即可获得三角形面积的表达式，最后利用函数性质求出三角形面积的最大值.

解法五：由(1)知抛物线C的方程为x2=4y.

因为点P在圆M：x2+(y+4)2=1上，所以可设点P(cosθ，sinθ-4)，从而可设切线方程为y=k(x-cosθ)+sinθ-4.

即16k2-4(4kcosθ-4sinθ+16)=0，

化简得k2-kcosθ+sinθ-4=0.

设两条切线PA，PB的斜率分别为k1，k2，则有k1+k2=cosθ，k1k2=sinθ-4，所以P(k1+k2，k1k2).

从而，点P到直线AB的距离

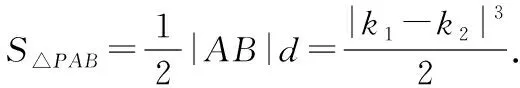
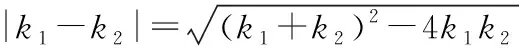
又因为-1≤sinθ≤1，所以当sinθ=-1时，

评注：该解法借助圆的参数方程设点，将问题进行适当转化，最终将三角形面积的最值问题转化为三角函数求最值，使得目标问题得以顺利求解.

思路6：此题还可以结合向量利用三角形面积的坐标公式进行计算.

引理证明如下：

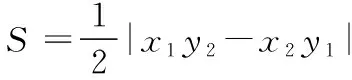
又P(m+n，mn)在圆M：x2+(y+4)2=1上，

由①②得(m-n)2=-sin2θ-4sinθ+17.

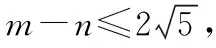
评注：利用三角形面积的坐标公式计算三角形面积运算量少，优化解法.在解题过程中运用二次函数最值思想和正弦函数的有界性.

2.性质探究

本题命题背景是抛物线的弦与过弦的端点的两条切线所组成的三角形，此三角形被称为阿基米德三角形.下面以抛物线y2=2px(p>0)为例，探究阿基米德三角形常考性质并加以证明.

命题：如图，过点P(x0，y0)引抛物线C：y2=2px(p>0)的两条切线PA，PB，切点分别为A，B，M为AB的中点.则有如下的性质：

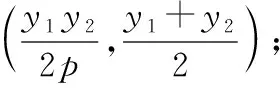
证明：设A(x1，y1)，B(x2，y2)，M为弦AB的中点，

则过A的切线为yy1=p(x+x1)，过B的切线为yy2=p(x+x2)，

性质2：PM∥x轴；

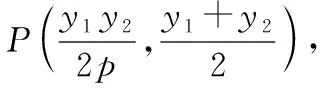
于是得到PM∥x轴.

性质3：切点弦AB的方程为yy0=p(x+x0)；

证明：因为过A的切线为yy1=p(x+x1)，过B的切线为yy2=p(x+x2)，

而点P(x0，y0)在切线PA，PB上，

所以y1y0=p(x1+x0)且y2y0=p(x2+x0)，

这表明点A，B均在直线yy0=p(x+x0)上，又经过两点的直线唯一存在，

所以直线AB的方程为yy0=p(x+x0).

性质4：若AB过定点(m，n)，则P的轨迹方程为ny=p(m+x)；

性质5：PM的中点Q在抛物线上，过点Q作抛物线的切线，该切线与AB平行；

设直线AB的方程为x=my+n，

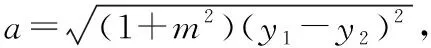
所以(y1-y2)2≤a2，

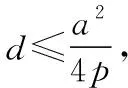
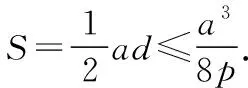
3.结语

在高考备考中，要深入研究研究经典命题，不仅包含理解试题考查的基本知识，求解的思想方法，更要探寻试题的命制轨迹，对一些经典的知识和方法进行拓展延伸，做到举一反三是很有必要的，它应该成为教师解题教学或习题课的一种常态.只有这样才能有助于我们正确把握高考的命题趋势，提升备考效率，于教学过程中落实学科核心素养.