重视“思维建模”能力培养 提升学生数学思维品质

甘肃 焦永垚

(作者单位:甘肃省兰州市第六中学)

新时代高中数学教学以发展学生的数学核心素养为目标，因此，高中数学教学对教师提出了新要求和新挑战，需要教师运用新的思维去面对，而“重视学生的思维建模能力培养”就是一条值得选择和探索的途径.在教学中重视数学思维建模能力培养有利于提升学生的数学思维品质，有利于发展学生的数学核心素养.

一、思维建模的自主构建与变式问题的教学功能相结合，培养学生思维的逻辑性与条理性

学生自主建构思维模型的过程就是在原有知识经验的基础上同化新知识的过程，在新课程理念下，高三数学复习课与“题海战术”渐行渐远，为了提高复习效率，教师往往要对千变万化的题目进行精挑细选，要讲究以少胜多，而变式教学就是解决这一问题的有效途径，我们只需将同一典型模式呈现在多种题目场景中设置变式问题，变式问题不仅要体现典型模式的共性，而且还要对比变式突出差异，这样才能在已有模式的基础上层层推进，思考差异，突破已有模式，克服思维定势.

【案例1】在“利用基本不等式求多元函数的最值”复习教学中，学生都熟悉如下基本模式：

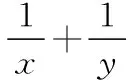
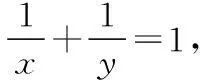
我们可以进行如下教学设计：

第一阶段：复习回顾，唤醒思维

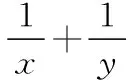
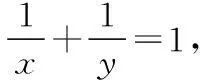
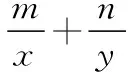
第二阶段：方法应用，构建思维

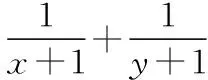
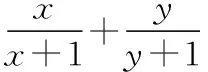
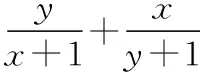
分析：(1)因为x+2y=1，所以

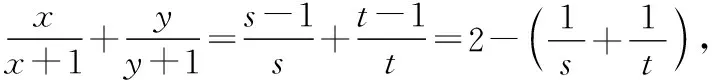
(3)因为x+2y=1，所以

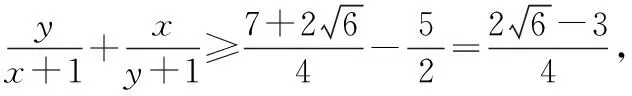
第二阶段的主要目的是在第一阶段熟悉模式和方法的基础上，继续鼓励学生一题多解，深刻体会解法之间的区别，以便合理选择最优解法.教师继续从学生的最近发展区入手点评，让学生体会“1的代换”的技巧，即利用“配凑”或“换元”的思想将目标函数化为“倒数结构”(思维模型如图所示)，从而为运用基本不等式创造条件.

第三阶段：归类巩固，发散思维

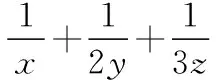
答案：9

答案：1

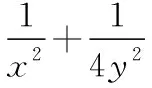
答案：6

经历了前两个阶段后，学生已经初步掌握了“1的代换”这一处理此类问题的基本方法和技巧，通过这一组反馈练习再进行综合训练，进一步发挥模型的作用，达到缩短解题路径的目的，从而提高了解题效率.

二、思维建模的路径优化与典型模式的解题功能相结合，培养学生思维的灵活性与敏捷性

对于学生而言，思维建模的方式因人而异，同一个问题可以从不同角度理解模式的特征，思维建模的方式会呈现出每个人各自的特色，因此教师要以培养学生思维的灵活性与敏捷性为目的，倡导多向思维，鼓励学生一题多解，引导学生“为问题建模”，然后根据问题的特点，并结合学生的思维水平和思维特征，引导学生合理选择最优解法，也就是找到一种让学生能够“以不变应万变”的方法，使解题步骤程序化.

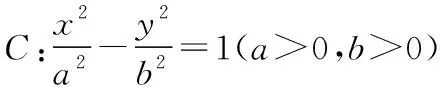
思路1：利用圆锥曲线的第一定义和解三角形的相关知识处理

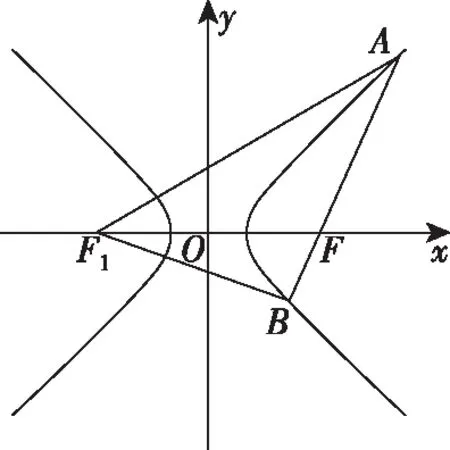
如图所示，设|FB|=m，则由题意可知|AF|=4m，|AB|=5m，设C的左焦点为F1，则由双曲线的第一定义可知|AF1|=2a+4m，|BF1|=2a+m.

在△AF1F和△BF1F中，

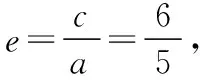
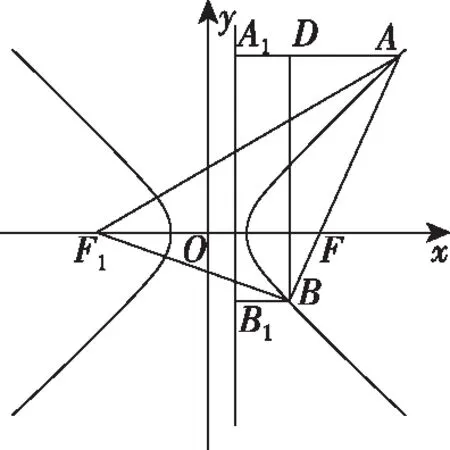
思路2：利用圆锥曲线和直线的位置关系处理

思路3：利用圆锥曲线的第二定义处理

思路4：利用直线的参数方程处理

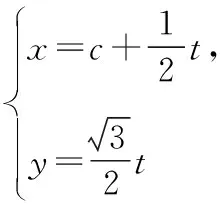
思路5：利用圆锥曲线的极坐标方程处理

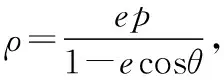
上述问题为圆锥曲线中与焦点三角形有关的离心率问题，此类问题在历年高考和竞赛中频繁出现，我们要引导学生对所积累的知识经验进行加工，形成对此类问题的认知模型，作为引领学生进行解题分析的典型模式.在教学中，教师要鼓励学生尝试多种解法，进而在各自的最近发展区内合理选择最优解法，只有如此，学生才能在遇到新问题时对原有的模型进行强化或修正，最终发展成更为完整的基本模型.为了进一步强化模型，我们还可以设计如下反馈练习进行训练，充分发挥模型的作用，让学生快速精准地选择自己脑海里的“最优解法”.

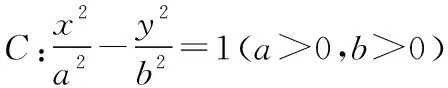
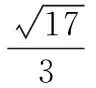
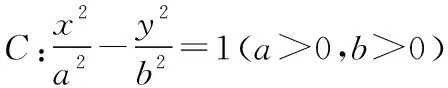
三、思维建模的方法选择与顺应解题自然的“特法”“巧法”相结合，培养学生思维的发散性与创新性

很多教师在解题教学中一味倡导“通性通法”，而刻意排斥“特法”“巧法”，殊不知“特法”“巧法”能在解题中起到化繁为简、事半功倍的作用.事实上，只要这些“特法”“巧法”顺应“解题自然”，符合学生的认知规律，那么我们不但不应该排斥，而且还要专门设计基于“解题自然”的“特法”“巧法”教学，促使学生将一些“特法”“巧法”主动纳入自己的认知模型中，使其变为属于自己的“通性通法”.

解法1(通法)：当直线EF的斜率为0时，E(-1,0)，F(3,0)，设P(x0,y0，则

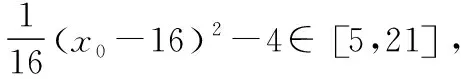
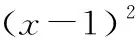
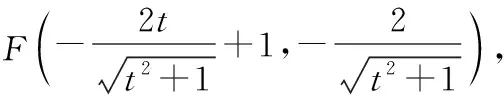
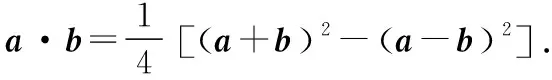
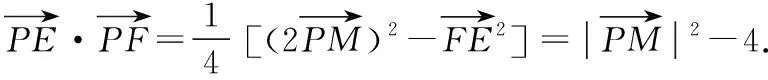
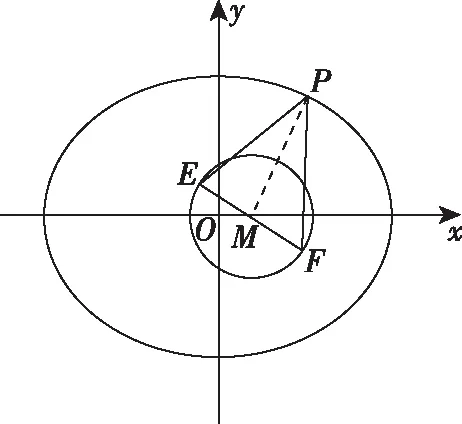
从解法2中可以看出，极化恒等式的优势在于将向量的数量积转化为线段长度的关系，大大地简化了运算，提升了解题效率.利用极化恒等式可以解决平面向量中的一些求数量积、求模、求最值等问题.为了让这些“巧法”适用于更多模型，我们需要在教学中揭示极化恒等式的来龙去脉和几何意义，引导学生总结归纳极化恒等式所适用的题型，激发学生对“巧法”的认同感，同时在应用中让学生感受极化恒等式的实用价值，进一步积累解题经验，从而最终将这些“巧法”内化为自己的“通性通法”.

四、思维建模的回顾反思与问题解决的数学思想相结合，培养学生思维的深刻性与批判性

【案例4】已知正数x,y,z满足x2+y2+xy=1，y2+z2+yz=2，z2+x2+zx=3，则x+y+z=________.

解析：如图所示，从O点出发，作长度分别为x,y,z的三条线段OA,OB,OC，且使∠AOB=∠AOC=∠BOC=120°.

一个复杂问题通常都是由一些小问题构成的，因此复杂问题的解题之道和思维建模的路径是一致的.对于一道复杂问题，我们不能仅仅满足于得到问题的结果，如果忽视了解题后的回顾反思，无异于“入宝山而空返”，就错过了再提升的机会.如案例4，在问题解决后，教师可以启发学生对思维模型的构建作如下回顾反思：

回顾反思1：对于这样一道解方程组的问题，我们通过挖掘方程的代数结构，将其与余弦定理联系，再构造几何图形解决.构造几何图形是解决数学问题的一种常用方法，此法能够把抽象的代数关系用图形直观地表示出来，从而快速抓住问题的本质，使复杂问题变得简单，充分体现了数形结合的优越性.构造几何图形解题不仅能够获得赏心悦目的解答过程，而且还可以提升直观想象核心素养.

回顾反思2：数形结合是一种非常重要的数学思想，“数形结合”具有双向性，我们既要进行代数抽象的探索，又要进行几何直观的分析，两者是密切联系、相辅相成的统一整体，而不是简单的“代数问题几何化”或“几何问题代数化”，在解题时要灵活应用.

回顾反思3：本题求解中，将已知方程与余弦定理联系是解题的关键，此类题目在各类考试中经常出现，通过巩固与练习更有利于提升学生的思维品质.

练习1:计算sin220°+cos250°+sin20°cos50°=_____.

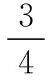
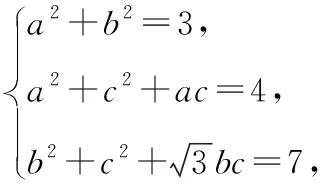
总之，将思维模型嵌入解题教学中，有利于学生更深刻地理解知识、更灵活地选择方法，从而更高效地解决问题，思维建模可以有效地提升学生思维的逻辑性、灵活性、批判性以及创新性，思维建模还可以有效地整合自身的知识经验，形成思维模型，并在不断地解题实践与反思中修正和完善，最终内化为属于自己的基本模式，在解题中可以“信手拈来”，达到得心应手的境界，从而发挥模型的最大价值.