新旧教材对比备考有的放矢
——以“立体几何”新旧教材内容变化的对比研究为例

2022-07-29 04:18山东尹承利

教学考试(高考数学) 2022年3期

山东尹承利

(作者单位：山东省泰安英雄山中学)

由人教社依据《普通高中数学课程标准(2017年版2020年修订)》编写的《普通高中教科书·数学》(以下简称新教材)，率先使用的省份(如山东省)已进入第3个年份，对于这些省份而言，2022年的全国数学新高考可谓是真正意义上新教材与新高考“同步”的首次高考.相比于《普通高中课程标准实验教科书·数学》(以下简称旧教材)，新教材在编写理念、顺序结构、内容编排等方面都有许多变化，有内容增加与删减、有顺序调整、有知识重构、有强调有淡化，对比研究、厘清新、旧教材的变化特点，对于使用新教材的新高考地区高三师生的临考复习备考有着十分重要的意义.本文以人教A版高中数学新旧教材为例，对“立体几何”教材内容的变化情况进行对比研究，并就临考复习备考中如何对待这些内容提出建议.

一、新旧教材对比

为了对“立体几何”新旧教材的变化情况有一个清晰的认识，首先对新旧教材“立体几何”在内容编排上做以下对比，内容变化由此便可窥见一斑.

内容编排对比

表1 新旧教材内容编排对比与新教材主要变化内容

续表

由表可以看出，新旧教材对于“立体几何”的整体框架和主干知识没有本质的变化，新教材相比于旧教材，在内容的编排上更趋于条理、更合乎规范.

二、新旧教材“立体几何”变化内容的分析研究

1.新教材没有出现“立体图形的三视图”的内容，但笔者理解这是一种“伪删除”.其一，立体图形的三视图是初中学过的，这次新教材中将其删除其实是和初中内容相衔接，避免重复，不算真正意义上的“删除”；其二，在课后练习题和习题中，仍有“三视图”的题目出现.因此，教学中要适度把握，既不能置之不理，也不能过于拔高，就像对待其他初中学习过的内容一样来对待“三视图”.

2.新旧教材“立体几何”的部分知识重构的内容受限于表格，在表中没有呈现，在这里列出，供教师在教学时予以关注.

(1)新教材必修第二册8.1中补充了直棱柱、正棱柱、正棱锥等概念，这样使得概念体系更完整了.

(2)新教材必修第二册8.5将基本事实4(平行公理)和(等角)定理纳入进来.

(3)新教材必修第二册8.5是先研究直线与平面平行的判定和性质，后研究平面与平面平行的判定和性质；旧教材是先研究直线与平面平行、平面与平面平行的判定，后研究直线与平面平行、平面与平面平行的性质.新教材的编排更为合理，这样可以避免学生在位置关系学习上的混淆.

(4)新教材必修第二册8.6也是先研究直线与平面垂直的判定和性质，后研究平面与平面垂直的判定和性质；旧教材是先研究直线与平面垂直、平面与平面垂直的判定，后研究直线与平面垂直、平面与平面垂直的性质.同样，新教材的编排更为合理，这样可以避免在位置关系学习上的混淆.

(5)新教材选择性必修第一册1.1-1.3将旧教材选修2-1的3.1分为三节内容编排，这样的编排使内容更清晰、条理，也更有梯度性.

3.新教材在一些概念的表述上更规范、清晰和明确.比如，必修第二册8.4-8.5将旧教材“公理”改为“基本事实”，并有顺序上的微调.选择性必修第一册1.4定义了“平面α与平面β的夹角”的概念，对于建立空间直角坐标系的表达，例题中有了清楚的“模板”；对于设平面法向量的表达形式比如：设平面α的法向量为n=(x，y，z)，而经过运算求出具体的法向量的表达形式，比如：(-2，0，1)为平面α的一个法向量，也有例题“范本”可以参照.

4.新教材选择性必修第一册1.3增加了“投影向量”的概念；1.4增加了直线与平面所成的角、平面与平面的夹角、点到平面的距离等向量公式，尤其对于增加的点到平面的距离的向量公式，复习备考中需引起特别重视，进行一些必要的训练是必要的.

三、需重点关注的几个内容

前面提到的新旧教材“立体几何”概念表述不同和新教材增加的内容中，有几个内容需要特别关注，在此对这些内容在新旧教材的说法进行对比分析，并探讨命题时说法上的不同.

1.投影向量

这一定义不仅告诉我们投影向量的概念，同时也告诉我们求投影向量的公式.

故|c|=3，即向量c的模为3.

2.二面角

无论是新教材还是旧教材，二面角是跨越必修模块到选择性必修(选修)模块的一个重要概念，而这一概念恰恰又是高考考查的重点，特别是新教材选择性必修第一册1.4对求二面角的说法上与旧教材相比有了很大的变化，这也是教师教学中一个需要特别关注的“点”.

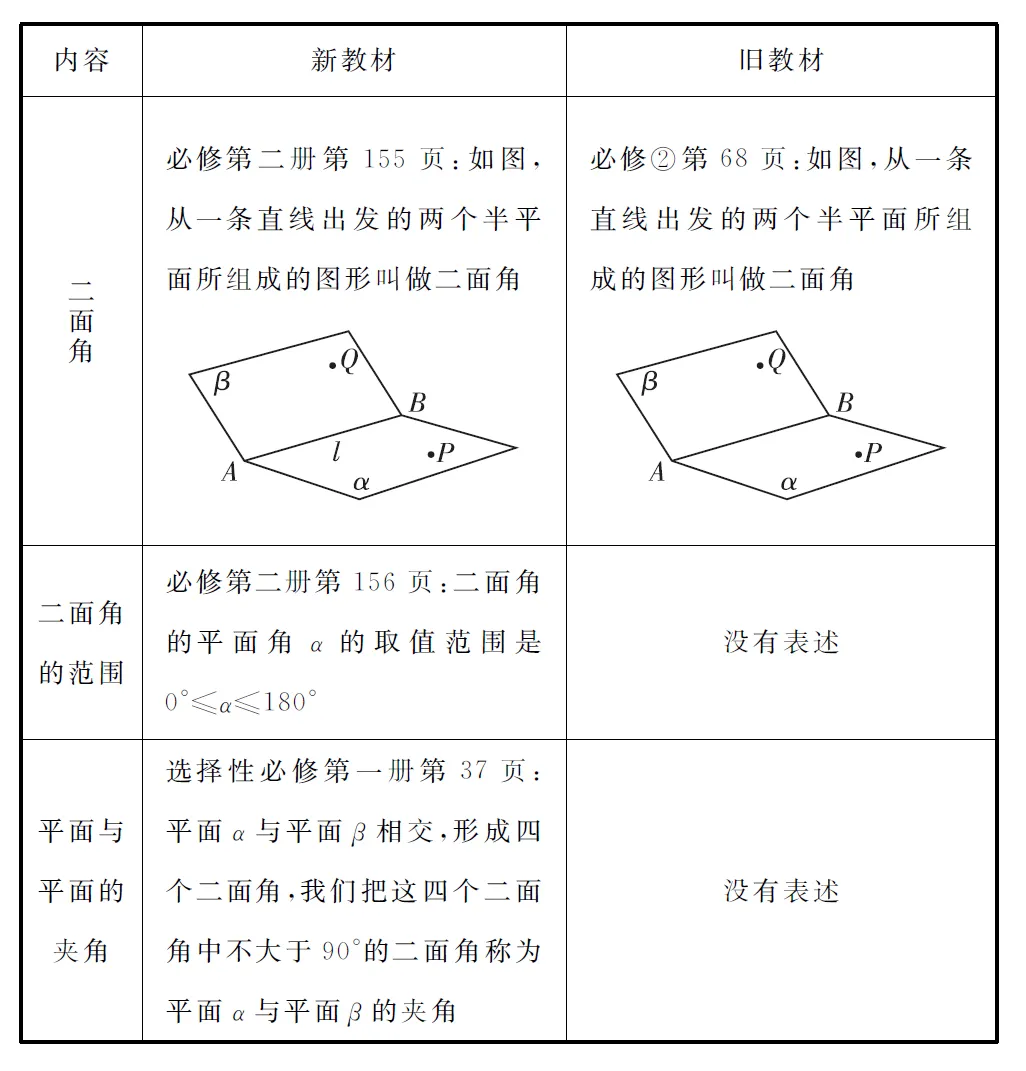
表2 新旧教材“二面角”内容变化对比

通过表2可以看出，关于“二面角”新旧教材最大的变化就是新教材选择性必修第一册1.4中给出了“平面与平面的夹角”的概念，这样应用向量法求“二面角”的有关命题时，只要将平面与平面的夹角转化为它们法向量的夹角，利用公式求解即可.而按旧教材求二面角，首先求出这两个面法向量的夹角，然后通过分析图形或推理确定是锐二面角还是钝二面角后得解.新教材这样的处理，不仅使得问题有明确的指向性，而且可以避免按旧教材求二面角时需要判断是锐二面角还是钝二面角的麻烦，避免歧义的出现.

我们先来看一道按旧教材命制的题目：

(1)求证:BE∥平面PDF；

(2)求二面角P-DF-C的余弦值.

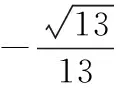
第(2)小题通过建立空间直角坐标系，并分别求出两个平面的一个法向量及这两个法向量所成的角后，需要判断二面角P-DF-C是锐二面角还是钝二面角，才能确定二面角的余弦值.

若按新教材命制题目：

(1)求证：BE∥平面PDF；

(2)求平面PDF与平面ABCD夹角的余弦值.

这样无需判断角的范围，直接按照平面与平面夹角的向量公式求得结论即可.

3.点到平面的距离

对于“点到平面的距离”问题，也是教学中需要特别关注的“点”.旧教材选修2-1只是在3.2的课后习题中出现了“求点到平面的距离”的问题，如第112页第5题(2)：求点O到平面ABC的距离.既没有前期的概念铺垫，也没有现成的公式应用，着实令人感到突兀.而新教材的处理就非常完备，新教材在必修第二册第150页给出了概念：“过一点作垂直于已知平面的直线，则该点与垂足间的线段，叫做这个点到该平面的垂线段，垂线段的长度叫做这个点到该平面的距离.”并在选择性必修第一册第33-34页给出了“点到平面的距离”的向量求法公式.可以说求“点到平面的距离”是新高考卷的又一新的命题点，教学中需加以重视.

四、复习备考建议

“新高考”伴随着新教材，对“立体几何”临考的复习备考何去何从？笔者认为，以往指导学生复习备考好的、有效的做法(这里不再赘述)在必须坚持的同时，也应改变教学观念，在着眼于提升学生的数学核心素养方面多做文章.

1.重视教材内容的变化

上面对新旧教材“立体几何”内容的变化进行了一些对比，临考复习中务必吃透这些变化，严格按新教材的新概念、新公式、新表达等进行复习备考，重视规范书写，防止“穿新鞋走老路”的情况发生.

2.关注“立体几何”新题型

新教材是数学核心素养导向下编排的，新高考定会重视“立体几何”命题的创新，尤其近期官方透露2022年高考命题指向，高考试题要优化情境设计，体现创新性.“立体几何”是创新命题的良好载体，临考复习备考要特别关注和研究“立体几何”新题型，在这里列举几例，以期抛砖引玉.

示例3：(2022·福州一中第一学期第一学段考·21)如图所示，在底半径为R，高为H(H，R为定值，且H≤R)的圆锥内部内接一个底半径为r、高为h的圆柱，甲、乙两位同学采用两种不同的方法来解决.甲采用圆柱底面与圆锥底面重合的“竖放”方式(图1)，乙采用圆柱母线与圆锥底面直径重合的“横放”方式(图2).

(1)设V1，V2分别“竖放”“横放”时内接圆柱的体积，用内接圆柱的底半径r为自变量分别表示V1，V2；

(2)试分别求V1，V2的最大值(V1)max，(V2)max，并比较(V1)max，(V2)max的大小.

简析：本题给出“竖放”和“横放”内接圆柱的两种不同的放置方法，利用轴截面图中的三角形相似，将内接圆柱的体积分别建立函数模型，求导，利用导数研究函数的单调性求得体积的最大值，最后作差比较两种方法的体积最大值的大小得到结论.本题从图形到设问方式都十分新颖.

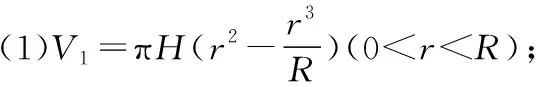
(V1)max>(V2)max

(1)求椭圆Γ的标准方程；

(2)如图，将平面xOy沿x轴折叠，使y轴正半轴和x轴所确定的半平面(平面AF1F2)与y轴负半轴和x轴所确定的半平面(平面BF1F2)互相垂直.

简析：本题以平面直角坐标系中椭圆的翻折为背景，通过分析翻折前后的关系，综合考查了椭圆的定义、直线与椭圆的位置关系等知识的应用及空间向量在求空间角中的应用，充分体现了解析几何和立体几何知识的创新交汇，是一道知识间创新融合的经典试题.

示例5：(2021·山东新高考质量测评联盟10月联考·17)如图，在四棱锥M-ABCD中，底面ABCD是平行四边形，且AB=BC=1，MD=1，MD⊥平面ABCD，H是MB中点，在下面两个条件中任选一个，并作答：

若________，求CH与平面MCD所成角的正弦值.

注：如果选择两个条件分别解答，按第一个解答计分.

简析：本题以三棱锥为载体，考查了空间线、面关系的推理判断和空间向量坐标法在空间线、面角度量中的应用.由于选择条件的不同，推理判断、建系和所得结论不尽相同.本题是结构不良试题从知识层面向立体几何知识模块进行扩展的一次实践，从知识层面上来说，给出了一种重要的命题导向.这就提醒新高考地区的广大师生，在复习备考中要有针对性训练的措施.

五、结束语