紧扣主线 高效复习——以数列前n项求和方法的复习为例

广西岑溪中学（543200） 钟 明

在新高考中，数列大题出现在第一道解答题的位置，更多的是关注基本方法、基本思想，其中裂项相消法和错位相减法是求数列前n项和的最基本的两类方法。数列前n项求和方法的复习至关重要。那么，如何有效开展数列前n项求和方法的复习呢？笔者认为，可紧扣知识、思想方法、核心素养三大主线进行复习。

一、紧扣知识主线进行复习

高中数学复习中，学生有两个基本任务，一是温故知新，二是查漏补缺。教师可指导学生从两个方面进行查漏补缺：一是数学概念、定理法则方面，梳理哪些还没有记住，哪些没有理解，哪些无法运用；二是数学思想方法和思维方法方面，厘清哪些还不会用或用得不够好。在复习数列前n项求和方法时，教师应紧扣知识主线引导学生梳理数列求和的常见方法。

（一）公式法

（二）分组求和法

当数列的通项是等差数列或等比数列的和（或差）的形式时，形如cn=an+b（n其中an和bn为等差数列或为等比数列），可以分解为基本数列（等差数列或等比数列）进行求和。

［例1］已知等比数列{an}中，若a1=3，公比q＞1，且3(an+2+an)-10an+1=0(n∈N+)。

（1）求数列{an}的通项公式；

评析：对于复合数列，若无法直接利用数列的通项公式求和，则可将其分解为几个容易求和的基本数列，对复合数列通项中的和（差）重新分组与拆分，再利用公式进行求和。

（三）裂项相消法

裂项相消法主要是把数列的通项拆分为两项之差后求和，正负相消剩下首尾若干项。应用此法时必须注意哪些项被消除，哪些项被保留，同时需要掌握一些常见的裂项，如（其中an为等差数列）。

［例2］Sn为数列{an}的前n项和，已知an＞0，an2+2an=4Sn+3。

（1）求{an}的通项公式；

解：（1）an=2n+1。

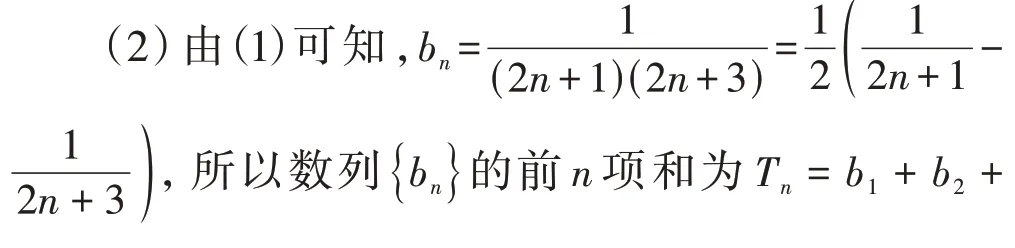
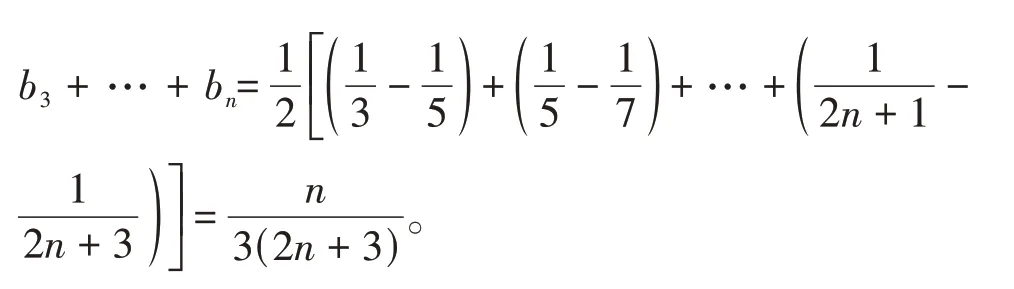
评析：根据an=2n+1 通项特点，得bn=，显然分母为等差数列相邻两项的乘积，符合裂项相消法的应用要求。

（四）错位相减法

对于由等差数列和等比数列对应项之积组成的数列，形如cn=an·b（n其中an为等差数列，bn为等比数列），常用错位相减法求和。可在等式两端同时乘以等比数列的公比（或公比的倒数后进行错位相减，再利用等比数列的求和公式化简求值。

［例3］设{an}是公比不为1 的等比数列，a1为a2，a3的等差中项。

（1）求{an}的公比；

（2）若a1=1，求数列{nan}的前n项和。

解：（1）{an}的公比为-2。（解题过程略）

评析：错位相减法适用于由一个等差数列{an}及一个等比数列{bn}对应项之积组成的复合数列。用错位相减法求解，常会因为步骤烦琐、计算量大，而导致漏项或添项以及符号出错等。因此在等式两边乘公比后，对应项的幂指数会发生变化，应将相同幂指数的项对齐，这样有一个式子前面空出一项，另外一个式子后面就会多出一项，两式相减除第一项和最后一项外，剩下的n-1 项是一个等比数列。

以知识为主线引导学生温故知新，可让学生更清楚各类数列前n项求和方法的基本特点和应用要求，同时强化学生对基础知识和基本技能的掌握。

二、紧扣思想方法主线进行复习

如果说新课的学习重在“把书读厚”，那么复习课则要“把书读薄”。把握知识和方法的本质是“把书读薄”的重要手段。要让学生搞清楚知识背后所蕴含的思想方法与思维方法，教师应指导、帮助、督促学生加强对思想方法与思维方法的梳理与比较。教师应紧扣思想方法主线引导学生复习数列前n项和的求法。

［例4］已知数列{an}满足a1=1，an+1=3an+1。

评析：本题考查了数列的概念、递推公式，等比数列的定义、通项公式，等比数列的前n项和公式和放缩法证明不等式，体现了化归与转化思想的应用。

［例5］已知数列an=n2·2n，求数列前n项和Sn。

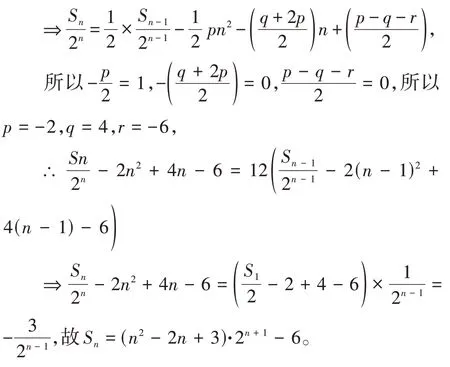
评析：让学生在原来的认知和知识框架下深化学习，把握数学知识中所蕴含的通性通法和数学思想。教师应通过审题示范、解题分析示范、解题反思示范，促进学生数学思维的发展，提升数学复习效果。

三、紧扣核心素养主线进行复习

在复习一些重要的知识与方法时，教师要尽量让学生多参与、多体会、多感悟，不断培养学生思维的深刻性，发展学生直观想象、逻辑推理、数学运算等学科核心素养。教师应紧扣核心素养这一主线引导学生复习数列前n项和的求法。

［例6］设等差数列{an}的公差为d，点(an,bn)在函数f(x)=2x的图像上(n∈N*)。

（1）若a1=-2，点(a8,4b7)在函数f(x)的图像上，求数列{an}的前n项和Sn；

评析：本题的第（1）问以函数为载体，以“点在函数图像上”为切入点得到数列的递推关系式，考查等差数列前n项和的知识。第（2）问以导数为工具，以曲线的切线方程为切入点，以“直线在x轴上的截距为为线索，利用方程思想求公差的通项公式识别“数学模型”，最终用错位相减法（或构造法）解决问题。本题有效考查了学生的直观想象、逻辑推理和数学建模等数学学科核心素养。

综上可知，在高中数学复习教学中，教师应紧扣知识、思想方法和核心素养三大主线引导学生进行复习，使学生把握数学本质和掌握数学知识、方法，进而发展学生的高阶思维，培养学生的数学学科核心素养。