一道试题的命制思路与解法赏析

福建莆田第一中学（351100） 蔡晶晶

在2021 年4 月初莆田市高三毕业班第二次市质检中，笔者有幸参与了第22 题导数压轴题的命制，收获颇丰，感触颇深，谨以此文与同行交流探讨。

一、原题呈现

设函数f(x)=2ex+acosx，a∈R。

（1）若f(x)在上存在零点，求实数a的取值范围。

（2）证明：当a∈[1,2]时，f(x) ≥2x+3。

二、命制手法

本题的第（2）小题是运用几何画板探究函数f(x)=2ex+acosx的图像与一次函数图像的关系时产生的命制思路。在通过对参数a不断调整取值时发现，当a∈[1,2]时，f(x)=2ex+acosx的轨迹恒在一条直线上方，通过拟合取整，可取该直线方程为y=2x+3，再进行严格论证可得出本小题结论正确。

三、解法赏析

第（1）小题的解法如下：

解法1（分类讨论法1）：

因此实数a的取值范围为(-∞,-2)。

第（2）小题的证法如下：

证法1（分类讨论法）：

当a∈[1,2]时，要证f(x) ≥2x+3，即证2ex+acosx-2x-3 ≥0。

令G(x)=2ex+acosx-2x-3，则G′(x)=2ex-asinx-2，G″(x)=2ex-acosx。

①当x≥0 时，G″(x) ≥2-a≥0，G′(x) 在[0,+∞)上单调递增，G′(x)≥G′(0)=0，所以G(x)在[0,+∞)上单调递增，G(x) ≥G(0)=a-1 ≥0。

综上所述，G(x) ≥0。

故当a∈[1,2]时，f(x) ≥2x+3。

证法2（变换主元法）：

当a∈[1,2]时，要证f(x) ≥2x+3，即证2ex+acosx-2x-3 ≥0。

设g(a)=(cosx)a+(2ex-2x-3)，故只需证对任意a∈[1,2]，有g(a) ≥0。

当x＜0 时，t(x) ＜0，即h′(x) ＜0；当x＞0 时，t(x) ＞0，即h′(x) ＞0，所以h(x)在(-∞,0)上单调递减，在(0,+∞)上单调递增。

因此h(x)≥h(0)=0，即2ex+cosx-2x-3 ≥0。

（ⅱ）再证2ex+2 cosx-2x-3 ≥0。

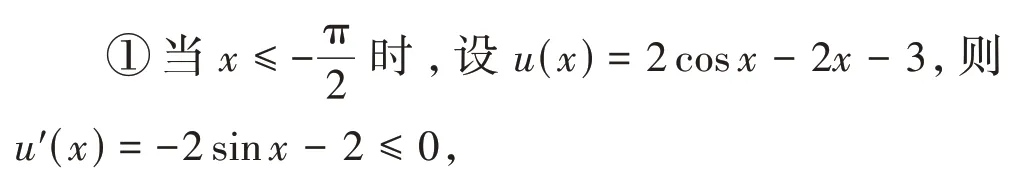
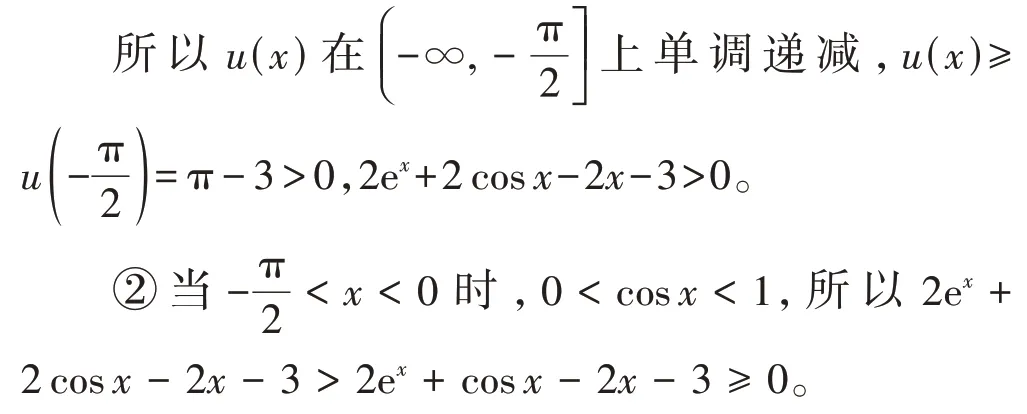
③当x≥0 时，设v(x)=2ex+2 cosx-2x-3，则v′(x)=2ex-2 sinx-2。

因为v″(x)=2ex-2 cosx＞0，所以v′(x)在[0,+∞)上单调递增，v′(x) ≥v′(0)=0。

因此v(x)在[0,+∞)上单调递增，v(x) ≥v(0)=1 ＞0，2ex+2 cosx-2x-3 ＞0。

综合①②③可知，2ex+2 cosx-2x-3 ＞0。

故当a∈[1,2]时，f(x) ≥2x+3。

证法3（分离参数法）：

笔者从直观想象的角度出发，改编了一道高三模拟题作为期末考试题。

改编前原题：已知函数f(x)=xex-a(lnx+x)。

（1）略；

（2）若a＞0，求f(x)的最小值。

解法1（隐零点法）：

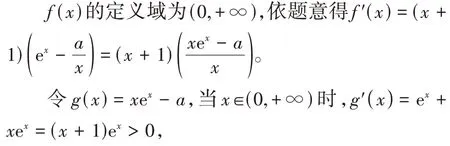
所以g(x)在(0,+∞)上为增函数。

由a＞0得g(0)=-a＜0，g(a)=a(ea-1) ＞0，所以g(0)g(a) ＜0，

故存在x0∈(0,a)，使g(x0)=0，即x0ex0=a，即lnx0+x0=lna。

因为g(x)在(0,+∞)上为增函数，

所以当x∈(0,x0) 时，g′(x) ＜g′(x0)=0，即f′(x) ＜0；

当x∈(x0,+∞)时，g′(x)＞g′(x0)=0，即f′(x)＞0，

所以f(x)在(0,x0)上为减函数，在(x0,+∞)上为增函数，f(x)min=f(x0)=x0ex0-a(lnx0+x0)=aalna=a(1-lna)。

解法2（同构函数法）：

由题意得f(x)=xex-a(lnx+x)=elnx+x-a(lnx+x)。

设t=lnx+x，则t∈R。

记φ(t)=et-at(t∈R)，故f(x)的最小值即为φ(t)最小值。

又φ′(t)=et-a(a＞0)，

当t=(-∞,lna)时，φ′(t) ＜0，φ(t)单调递减；

当t∈(lna,+∞)时，φ′(t) ＞0，φ(t)单调递增，

所以f(x)min=φ(lna)=elna-alna=a-alna。

改编后试题：已知函数f(x)=xex-a(lnx+x)（a＞0）。已知f(x)有两个零点，求a的取值范围。

解：同上可知f(x)min=f(x0)=x0ex0-a(lnx0+x0)=a-alna=a(1-lna)。

①当0 ＜a≤e 时，有f(x)min=f(x0)≥0，所以f(x) ≥0，此时f(x)在(0,+∞)上至多只有一个零点，不合题意，舍去。

②当a ＞e 时，有f(x)min=f(x0)＜0，由x0ex0=a，得1 ＜x0＜a。

又因为f(x)在(x0,+∞)上为增函数，所以f(x)在(x0,+∞)上存在唯一零点x2，f(x)在(x0,+∞)上有两个零点。

综上所述，a的取值范围为(e,+∞)。

以下同解法一。

四、命题感悟

正所谓“数缺形时少直观，形缺数时难入微”。以上试题遵循“低起点、多层次、高要求”的命题原则。从直观想象入手研制试题，发现不论是分类讨论法还是分离参数法，或是变换主元法，或是隐零点法，抑或是同构函数法，都是常用方法。多角度、分层次地探索解题思路，引导学生学会有逻辑地、创造性地思考，善于把握本质、以简驭繁，能发展学生的理性思维，培养学生的科学精神，提升学生分析和解决问题的能力。