处理圆锥曲线问题的几个关键点

安徽合肥市第九中学（230001） 殷春生

圆锥曲线问题是考查学生思维能力和计算能力的重要载体，在高考中常以压轴题的形式出现。学生在解决此类问题时，常常因为方向不明确或思路不正确，致使解题有始无终。基于此，笔者提出处理此类问题需要把握的几个关键点，并引例说明。

［例1］已知椭圆的离心率为，左、右顶点分别为A,B，点M是椭圆C上异于A,B的一点，直线AM与y轴交于点P。

（1）若点P在椭圆C的内部，求直线AM的斜率的取值范围；

（2）设椭圆C的右焦点为F，点Q在y轴上，且AQ ∥BM，求证：∠PFQ为定值。

一、解题方向要准确无误

定点、定值和最值问题是历年高考重点考查的题型。本题第（2）问要求证明∠PFQ为定值，有些学生认为这个角可能为特殊角，如等，想到利用正弦定理、余弦定理等解三角形的有关知识求解，进而要求△PFQ的其他边或角。因M是动点，所以点P、Q的位置不确定，要表示P、Q的坐标需要引入变量，再利用两点间距离公式求边长，即使可以表示出来，但不容易消元，计算烦琐。

类似地，判断一个角是锐角、钝角、直角时，均可采用此种方法。

二、方法选择要心中有数

圆锥曲线问题的求解思路，总的来说有两种：一是引入直线方程，设出交点坐标，将其与曲线方程联立，代入消元，结合判别式得出根与系数的关系，结合题目条件列出关系式，再代入根与系数的关系进行求解；二是采用设点法求解，即设出动点坐标(x0,y0)，将其他相关点的坐标用x0,y0表示，再结合题目条件列出关于x0,y0的关系，最后将x0,y0代入曲线方程，据此进行消元处理。

本题中的动点是M，因M的变动，使得P、Q随之变动，因此可采用设点法求解。具体解题过程如下：

本题在求解点Q的坐标时，也可利用直线BM与BQ的对称性，即先求出直线BM与y轴的交点的坐标，再利用点Q与该点的对称关系得出点Q的坐标。

三、隐含信息要挖掘清楚

本题能不能采用设直线的斜率k的方法来求解？答案是肯定的。这需要对题目中隐含的信息进行挖掘。本题中所隐含的信息在教材习题中有所体现。

［例2］（人教版高中数学教材A 版选择性必修1 练习）已知点B(6,0)，C(-6,0)，过点B的直线l和过点C的直线m相交于点A，设直线l的斜率为k1，直线m的斜率为k2，如果求点A的轨迹方程，并说明此轨迹是何种曲线。

此习题可推广到一般的情况。

［例3］已知点B(-a,0)，C(a,0)(a＞0)，过点B的直线l和过点C的直线m相交于点A，设直线l的斜率为k1，直线m的斜率为k2，如果求点A的轨迹方程，并说明此轨迹是何种曲线。

利用上述求解方法可得点A的轨迹方程为

对此结论进行逆向探究，可得出如下结论：

结论1已知椭圆的左、右顶点分别为A、B，M为椭圆上不同于A、B的一点，则直线AM、BM的斜率之积为定值

而例1 所给的条件，恰好符合这一结论，故可采用设直线斜率的方法求解。

例1 的另外解法：设直线MA的斜率为k，则直线MA的方程为y=k(x+2)，令x=0，则y=2k，即点P(0,2k)。

教材中的例题、习题都具有典型性，其中隐含着重要的知识、结论，包括解题的方法。因此，广大教师在教学中要尊重教材，充分利用教材，并引导学生主动探究教材，充分发挥教材的最大作用。

四、结论探究要进行彻底

上述结论也可以推广到更为一般的形式，即只要A、B两点关于坐标原点对称，此结论仍然成立。

结论2已知椭圆A、B是椭圆C上关于原点对称的两点，M为椭圆上与点A、B不重合的一点，若直线AM、BM的斜率存在且不为0，则直线AM、BM的斜率之积为定值

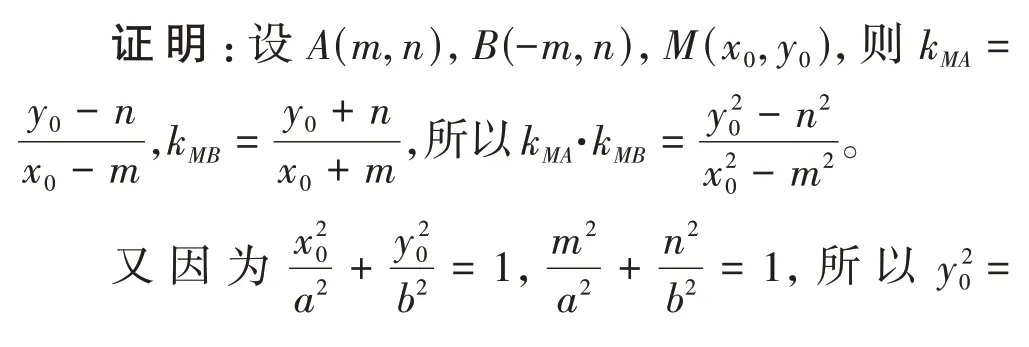
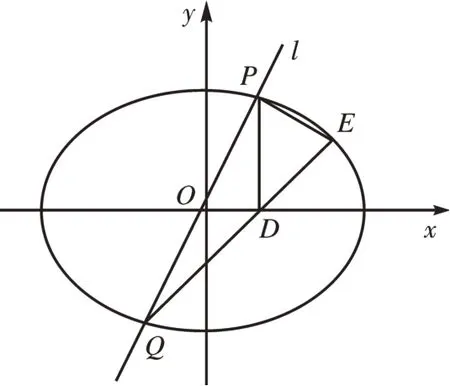
图1

（1）求椭圆C的方程；

（2）直线l过坐标原点O，且不与x，y轴重合，交椭圆C于点P,Q，过点P作x轴的垂线，垂足为点D，连接QD并延长交椭圆C于点E，试判断直线PE和l的斜率乘积是否为定值。若为定值，请求出该定值，否则请说明理由。

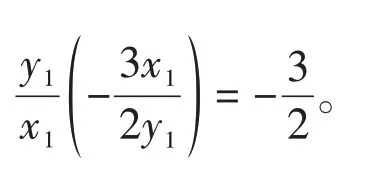
即PE和直线l的斜率之积为定值

本题中椭圆上的点P与点Q关于坐标原点对称，所以直线PE与QE的斜率之积为定值。只要我们心中有这个结论，解题的方向也自然就明确了。

类似地，在双曲线中也存在这一结论。

计算量大是圆锥曲线问题的重要特征，因此在解决圆锥曲线问题时除了要注意上述几个关键点，还要做到准确计算。

总之，圆锥曲线问题虽然形式多变，方法灵活，但是只要我们能够准确把握好关键点，就能以不变应万变，顺利、准确地解决问题。