圆锥曲线压轴题的处理策略
安徽阜阳市阜南一中(236300) 应 莉
本文以2020 年新课标Ⅰ卷(山东)第22 题为例,从解题方向的确定、解题方法的寻找和问题的拓展三个视角谈谈圆锥曲线压轴题的处理策略。
[例1][2020 年新课标Ⅰ卷(山东)第22 题]已知椭圆的离心率为,且过点A(2,1)。
(1)求C的方程;
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足。证明:存在定点Q,使得|DQ|为定值。
一、解题方向的确定
确定正确的解题方向是成功解题的关键。解题是从审题开始的,那么审题要审什么呢?总的来说,要审条件、审结论、找关联。本题的主要条件是M,N是椭圆C上两点,A为已知点,可将问题转化为一条直线与椭圆C交于M、N两点,且AM⊥AN。由AM⊥AN,可得直线AM和AN的斜率之积为-1。
椭圆有下面的性质:
M,N是椭圆上关于原点对称的两个点,P为椭圆C上不与M、N重合的点,若MP,NP的斜率存在且不为零,则kMP·kNP=
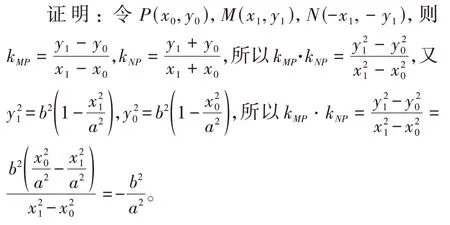
由该性质不难得出如下推论:
直线l与椭圆N两点,P为椭圆C上不与M、N重合的点,若kMP·则直线l过坐标原点。
证明方法同上,省略。
如图1 所示,若直线MN过定点,设该点为E,因为A为已知点,所以|AE|为定值,而AD⊥MN,所以△ADE为直角三角形,或所求的点Q为AE的中点,则,为定值,进而问题得解。

图1
从上述分析来看,解题方向并不是盲目确定的,而是与我们熟悉的内容建立关联。通过研究不难发现,很多高考题都是以我们熟悉的知识为背景,只要我们明确这些背景,解题方向的确定也就水到渠成了。
二、解题方法的寻找
以直线与圆锥曲线相交为背景的考题,常规解法是先引入直线方程,将其与椭圆方程联立,再利用坐标法、消元法、判别式及根与系数的关系等,结合所给的条件建立关联进行求解。
解法1:
(1)求得C的方程为
(2)当直线MN的斜率存在时,设其方程为y=kx+m,联立


本题是由斜率之积为定值(该定值为-1)引发的定点问题,事实上斜率之积为定值(不一定为-1)也能引发定点问题。解法2 采用了“齐次化”的方式,大大地简化了运算。
三、问题的拓展
类似的问题还有很多,我们可将斜率之积为定值变换为斜率之和为定值。另外,也可以将曲线类型变换为双曲线或抛物线进行探究,从而拓展视角。
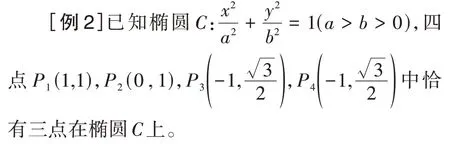
(1)求椭圆C的方程;
(2)设直线l不经过点P2且与椭圆C相交于A、B两点,若直线P2A与直线P2B的斜率和为-1,证明:直线l恒过定点。
解析:
(1)因为P3,P4两点关于y轴对称,所以由题设知椭圆C经过P3,P4两点。

(2)方法1:设直线P2A与直线P2B的斜率分别为k1,k2,如果直线l与x轴垂直,设直线l:x=t,由题设知t≠0,且 |t|<2,可得A,B的坐标分别为

[例3]已知抛物线C:y2=2x和点P(2,2),A、B是C上异于点P的两点,直线PA、PB的斜率分别为kPA,kPB,且满足kPA·kPB=2,则直线AB过定点( )。

[例4]已知抛物线C:y2=2x和点P(2,2),A、B是C上异于点P的两点,直线PA、PB的斜率kPA,kPB满足kPA+kPB=0,则直线AB的斜率为( )。

圆锥曲线问题虽然常考常新,但万变不离其宗,只要把握题目条件特征,化陌生为熟悉,即可明确解题的方向,确定解题的方法。将问题的曲线类型进行拓展,构建知识网络,可有效拓展学生的解题思路,提升学生分析问题和解决问题的能力。

