基于Arnold变换的数字影像隐私信息置乱方法研究

姜希尧

（上海工艺美术职业学院，上海 201808）

1 引言

信息置乱变换既能够作为信息加密手段，还能作为隐藏信息的预处理过程。因此，其越来越受到学术界探究的广泛关注[1]。

数字影像是利用有限数字数值像素来表达二维图像，运用数组或矩阵进行描述，光照位置与强度均呈现离散性[2]。数字影像通过模拟图像数字化获得，将像素当作基础元素，用数字计算机或数字电路保存及处理的图像。从数学角度来看，二维矩阵就是一幅数字图像，图像置乱就是把固定的数字图像转变为一幅杂乱无章的图像，令其表示的信息无法被直观获取。

关于图像置乱问题，郭海儒[3]等人基于像素颜色置乱，提出一种全新加密方法。采用新型增强量子模型表示彩色量子图像，再通过改进后的量子旋转门来阐明颜色的量子比特随机旋转，让初始图像不涵盖自身信息，达到加密效果。但该方法抗干扰性较差，算法性能稳定性不高。屈凌峰[4]等人利用加密前后明文图像0、1分布比例不变的特性，估计位平面置乱次序，再按照块置乱和块内像素置乱维持像素值恒定不变的特征，定义图像块均方根特征以查找和估计块置乱矩阵。但方法置乱过程计算量过大。

针对上述方法的不足，本文提出一种基于Arnold 变换的数字影像隐私信息置乱方法，在了解Arnold 变换计算过程前提下，使用离散化对其安全性与灵活性进行优化，然后对图像隐私信息的位置与色彩进行置乱处理，获得高质量置乱加密图像。

2 置乱方法研究

2.1 Arnold变换计算

Arnold变换又被叫作猫映射，将该变换过程记作：

式中，mod1代表仅择取小数部分，所以(xn，yn)的相空间被收敛于单位正方形[0，1]×[0，1]中，将其定义为矩阵模式：

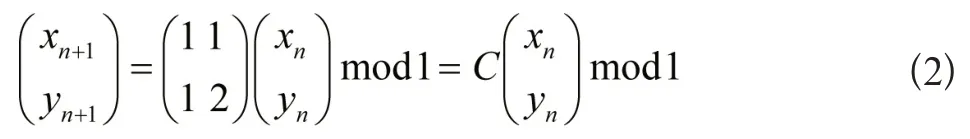
式中，C代表变换矩阵，行列式的值是1。此映射为无吸引子的单一映射，单位正方形中随机一点仅能变换至单位正方形中的另一点[5]。实际上，猫映射就是混沌映射，其指数经过推算矩阵C的两个特征值获得。

因为离散化下的Arnold 变换状态空间较为有限，难以拥有优秀的混沌特征。但从几何角度来看，依旧具备Arnold 变换的拉伸与折叠性质，致使邻近的两点(i，j)、(i，j+1)通过多次离散变换迭代后无法相邻，证明Arnold 变换拥有相对的初始值敏感性[6]。使用该性质，能打乱数字图像的相邻像素方位，从图像内不能得到原始图像的有关信息，实现隐私信息安全保护。

为增强Arnold变换作用于数字影像置乱的灵活性与安全性，对变换矩阵C内每个元素进行参数化，并符合相关收敛条件，得到广义Arnold变换：

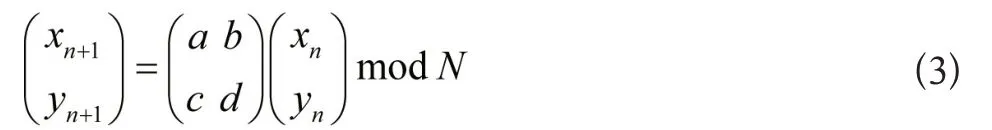
式中，参变量a，b，c，dC，且gcd(ad-bc，N)=1。然后将其变化成等价模式：

式中，l1、l2为整数。使用求解线性方程组的消元法求解上式，得到广义Arnold变换的逆向变换解析式：

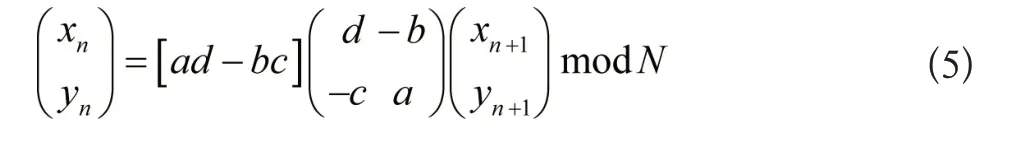
此外，关于整数型方程组式(4)，能够获得接近传统克莱姆法则的求解过程为：

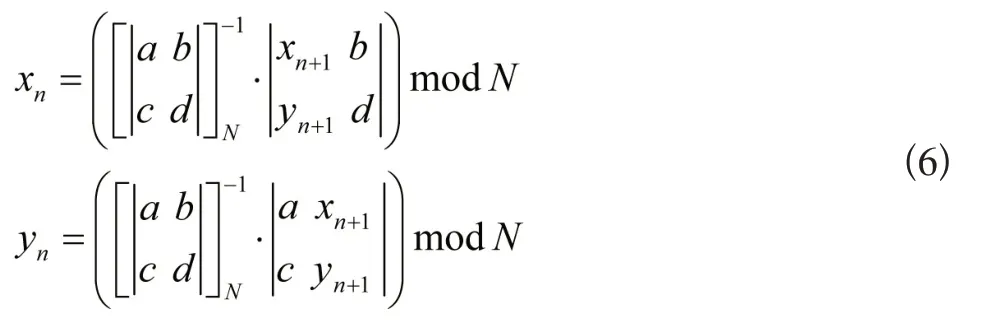
利用矩阵计算法，可判断出逆向变换下的式(5)与式(6)为等价关系，把逆向变化式(5)用在置乱后图像的迅速修复，比使用周期性修复具有更高的效率。关于二维广义Arnold变换只适用于两个变量的平面图像像素位置置乱的缺陷[7]，使用广义三维Arnold 变换来填补其不足，将广义三维Arnold变换过程记作：

式中，矩阵C表示变换矩阵，同时符合如下收敛条件：参变量均为整数值，且变换矩阵C的行列式满足式(8)条件。

在符合式(8)的前提下，让广义三维Arnold 变换拥有周期性、保面积性与可逆性。对于广义三维Arnold 变换的一般情况，相关学者设计了比较繁杂的消元法获得对应的逆向变换结果，但不利于理论研究与真实运用。依旧采用传统克莱姆法则进行求解[8]，满足高质量数字图像隐私信息保护，计算过程为：

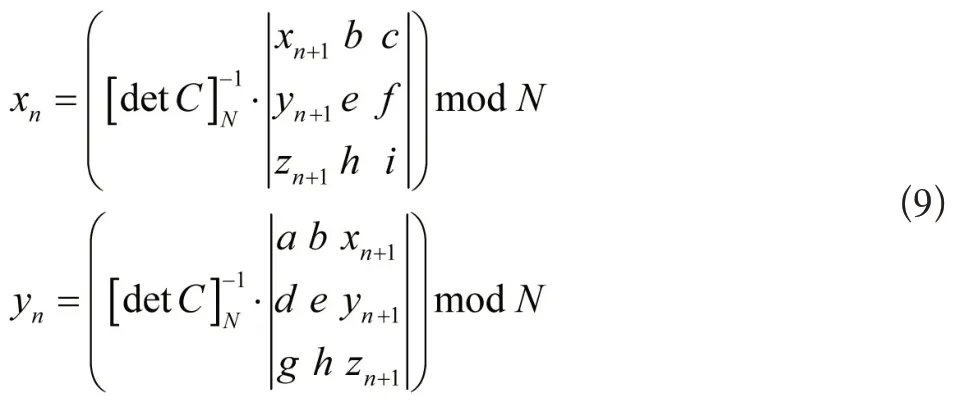
不管是二维广义Arnold 变换还是高维广义Arnold 变换，其数学性质均接近仿射变换，拥有线性密码学特质，安全性与置乱加密成效还有很大的提升空间，为优化Arnold 变换整体效果，对广义Arnold变换实施优化。混沌动力学中，有一类映射被叫作标准映射，将其描述成下式：

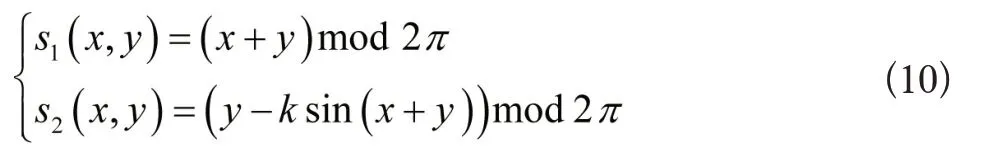
式中，k表示正常数，将式(10)变换成普通形式：

为实现数字影像像素值大小加密，将式(11)进行离散化，得到：

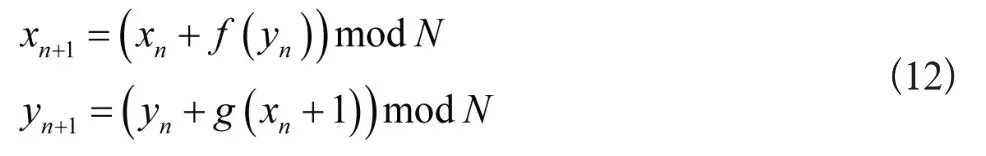
上述流程和传统密码学内的分组密码Feistel 结构十分相近。为使用离散标准映射来改进广义Arnold 变换提供了优化思路，具体优化过程为：将式(3)的广义Arnold变换转变为：

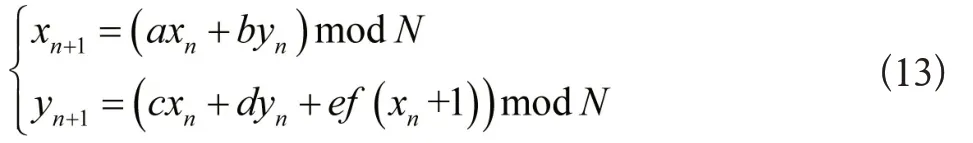
式中，f(xn+1)为非线性函数。此外，为提升Arnold 变换安全性能，对式(13)进行变换，剔除模计算过程，记作：

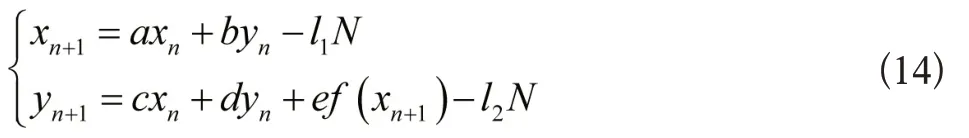
在上式成立的情况下，对其实施逆向变换：

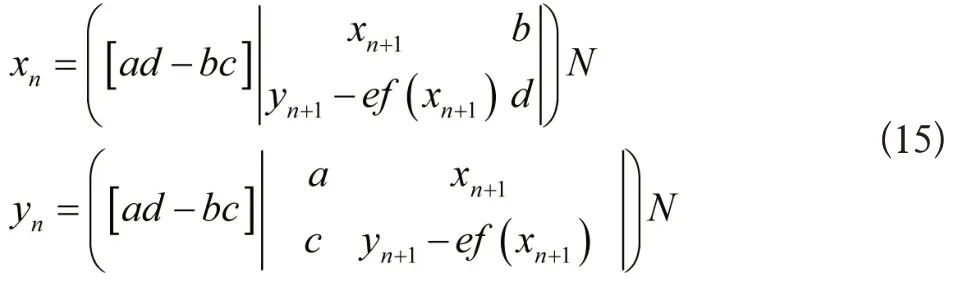
同理关于式(7)，能够得到提升其安全性的改进后变换解析式：

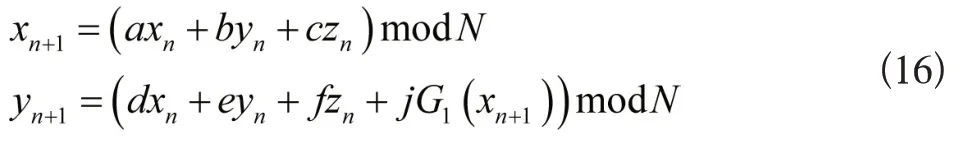
2.2 基于Arnold变换的数字影像隐私信息位置置乱

在了解Arnold变换相关计算过程后，下面对Arnold变换下数字影像隐私信息位置置乱进行着重研究。对于数字影像而言，可以把它当作某函数处于离散网格点的采样值，这样就能获得一个代表图像的矩阵。将正方形数字影像位置的离散化Arnold变换描述为：

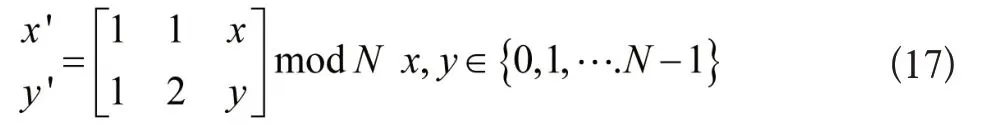
式中，N表示数字影像的宽度与高度。

数字影像内的位移本质上为互相对应点的灰度值或颜色值的位置移动，也就是把原始点(x，y)位置像素对应的灰度值转移到变换之后的点(x'，y')。倘若对某数字影像迭代采用离散化Arnold 变换，把左端输出的(x'，y')T当作下次变换输入，反复执行该操作，迭代若干次后，假如呈现的图像满足对其杂乱无章的需求，即完成数字影像隐私信息位置置乱目标。

值得注意的是，Arnold变换具备周期性，也就是迭代某个步骤之后，会重新获得初始图像，为解决这一难题，设定随机N＞2 情况下，Arnold 变换周期为TN≤N2/2。针对二维平面内的位置变换，可以通过Arnold 变换扩展出一类变换，符合此类位置移动需求。关于式(18)的矩阵，其元素符合ad-bc=1条件的情况下，对平面坐标实施转换就是一种置乱处理。

2.3 基于Arnold变换的数字影像隐私信息色彩置乱

把Arnold变换拓展至高维空间，与其对应的变换矩阵是：

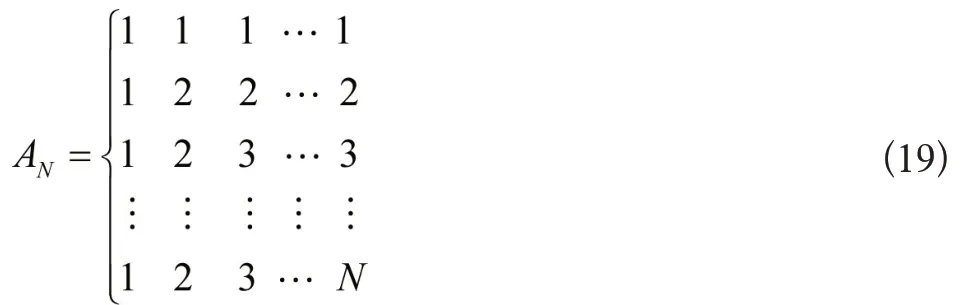
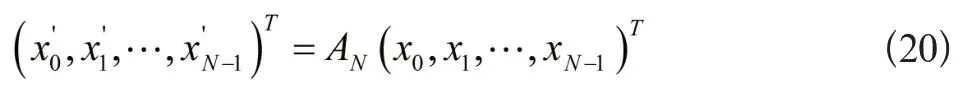
式(20)即为一种在N维空间内离散网格点的运动形式。在数字影像色彩空间中，设计两类高维Arnold 变换的置乱方法。首先是RGB色彩空间下的置乱方法。将三维空间内的正方体拟定为RGB 色彩空间，且顶点坐落于坐标原点，一般情况下，色彩空间中的颜色分量均为整数，因此置乱对象为正方体内的离散网格点，将其记作：

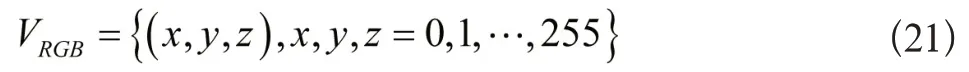
针对上面的RGB颜色，采用三维Arnold变换在该网格上实施置乱，实现对数字影像的颜色置乱效果：

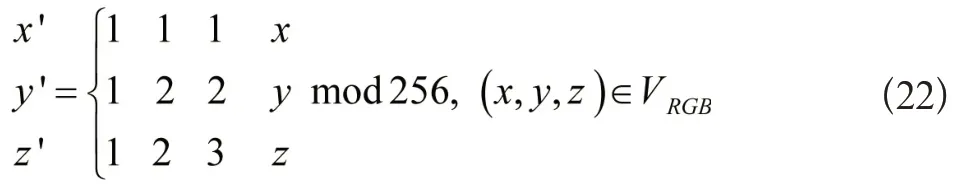
在RGB色彩空间内，假如使用上式进行变换，可以明确其周期为450。但对于数字影像来说，由于不同影像的色彩搭配各不相等，只能认定该周期为变换的一个临界值。色彩置乱的另一个难题为：不同位置的相同颜色不能实施置乱，这是由于R、G、B分量值为固定的，通过此种置乱变换后，不同位置点的色彩依旧相同，这样就恢复了初始图像的轮廓，对该问题使用下面的置乱方法进行修正。

设定某数字影像为F，把该影像描述成一个函数在矩形网格点处的函数值，即：

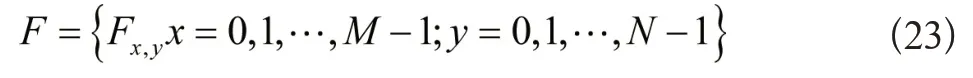
将该数字影像表示成以下矩阵：

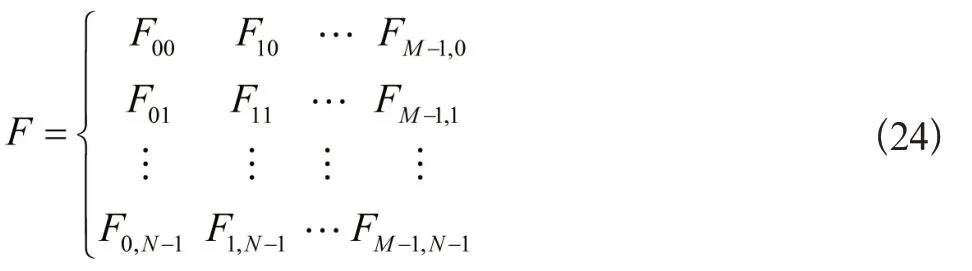
以列举例，随机挑选数字影像的某一列Z=(Fi0，Fi1，…，Fi，N-1)T，使用式(19)的N阶拓展Arnold变换矩阵AN采取以下变换过程：

利用式(25)就能获得一幅色彩置乱图像，把左端的输入列放置到初始图像的对应方位，并迭代重复该过程。

N维空间的拓展Arnold 变换周期计算过程比较繁杂，且因为影像不同的行与列，会出现多种色彩值组合排序，让初始图像恢复变得极其困难，恶意攻击者很难破译图像信息。由此看出，使用Arnold 变换时，即便是相同颜色，只要出现于图像内的不同方位，就能产生全新的色彩，让图像变得更为混乱，实现预期需求，填补了传统RGB色彩空间三维颜色置乱的缺陷。

3 实验与分析

为验证基于Arnold变换的数字影像隐私信息置乱方法的有效性，设计如下实验。

使用本文方法对512×512 的人像进行仿真实验，实验结果如图1 所示。图1(a)为初始图像，图1(b)是初始图像通过15 次Arnold 变换后，对其各个2×2 字块依次采取一次Fermat数变换后的结果，图1(c)为还原后的图像。分析图1可知，使用本文进行数字影像置乱后，该图像杂乱无章，拥有优秀的隐私信息安全性，且还原后的图像清晰度更高。

图1 本文方法的信息置乱效果图

表1为在图像大小不定的情况下，加解密所消耗的时间对比。分析表1 可知，本文方法的时间复杂度很低，证明所提图像置乱方法的运算速度较快，这是因为本文方法采用了Arnold 变换对所需加密图像进行置乱处理，并运用矩阵计算法改善图像修复速率，获得令人满意的图像加密结果。

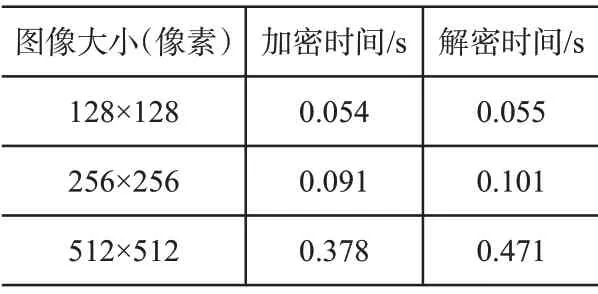
表1 本文方法加解密速率仿真结果

倘若初始图像像素点通过置乱变换后，像素点地址无任何改变，将该像素点当作置乱变换的不移动点。不移动点数量越少，置乱成效越好，保密性越强。表2 为对512×512 的lena 图像任意挑选的9000 个初值，经过Arnold 变换后不移动点的统计结果。分析表2可知，基于Arnold变换的数字影像隐私信息置乱方法的不移动点数量仅占据整幅图像全部像素点的0．37%～0．46%，证明本文方法拥有优秀的置乱效果，实用性强。

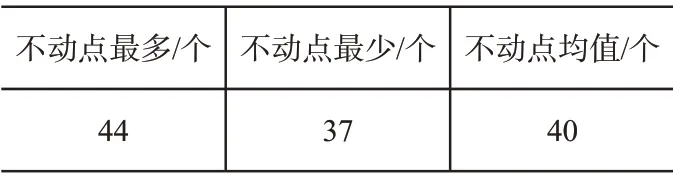
表2 图像置乱不移动点统计结果

4 结束语

针对数字影像隐私信息安全问题，本研究设计了基于Arnold变换的数字影像隐私信息置乱方法。该方法拥有计算量少、运行速率快、置乱效果良好等诸多优势。由于在还原图像块聚合特征时存在噪声，因此，在提升置乱效率的同时增强该方法在多样化应用背景下的适用性是接下来研究的主要内容。