带输入约束的一阶采样多智能体系统包含控制＊

张 旺,侯海良

（湖南人文科技学院信息学院，湖南 娄底 417000）

1 引言

近几年来，随着通信技术的快速发展，多智能体系统分布式控制已经成为控制中的一个研究热点问题，并取得了一些有价值的成果[1-4]，文献[1]研究了固定拓扑下的有限时间一致性问题。文献[2]研究了无向切换拓扑的有限时间一致性问题，证明了通信拓扑并集为联合联通图时能实现一致。前面的研究都是针对无领导者一致性问题，但在实际应用中单领导者系统会在减少系统开销的同时缩短收敛时间。在跟随者不能直接获得领导者状态情况下，文献[3]设计了一种基于邻居状态估计的一致性算法。文献[4]将文献[3]中结果扩展到二阶系统中，设计二阶观测器实现了噪声环境下对跟踪误差的估计。

近年来，随着实际应用要求的提高，有些工作任务需要多个领导者共同协调引导完成，包含控制等分布式协调控制问题逐渐引起人们的关注。包含控制指多个领导者形成一个凸包，通过设计分布式协调控制算法使所有跟随者进入凸包并最终保持在该凸包中。由于包含控制的潜在应用价值，如无人机护航编队、武装机器人执行护卫任务等，一些研究成果相继报道[5-10]。在连续系统包含控制问题上，文献[5]中研究了二阶系统在时变时滞影响下的包含控制问题，针对动态领导者和静态领导者分别提出了实现包含的时滞上界。文献[6]研究了在时变延迟情况下的包含控制问题，给出了通信拓扑图联合连通情况下实现包含控制的充分条件。文献[7]中解决了噪声影响下的包含控制问题。文献[8]研究了固定和切换有向网络拓扑两种情况下的包含控制问题，给出了实现包含控制的充分条件和必要条件。文献[9]分析了带有延迟的一阶离散时间系统的包含控制问题，提出了一种含单积分器的控制算法。文献[10]研究了一阶和二阶离散系统有界时滞包含控制问题。

以上文献研究均是针对连续多智能体系统[5-8]和离散多智能体系统[9-10]。但在实际控制时，连续多智能体系统数据传输和控制对信道的带宽和可靠性要求高，离散系统能有效的减少通信开销。考虑到实际系统通常是连续时间系统，而当今数字化时代控制器通常为采用计算机或者微处理器实现的离散数字控制器，其控制合成只需要使用离散的采样数据。因此，多智能体控制系统实际上是一种采样系统。与连续控制系统相比，采样系统只需要传输有限的采样数据，能明显降低通信代价。目前很少有针对采样多智能体包含控制问题的研究。文献[11]研究了仅利用位置信息的二阶采样系统的包含控制问题。文献[12]在文献[11]的基础上研究了采样延迟的包含控制问题。文献[13]针对通信延迟和切换拓扑的问题提出了一种基于投影的非线性算法。这些研究结果都认为智能体的输入和状态是不受约束的。实际上，由于物理条件的限制，智能体不可避免的要受到一些约束，比如无人机的速度只能在一定范围内变化，由于物理条件的限制控制输入也不可能无限大。因此，研究多智能体的约束问题具有重要的现实意义。文献[14]研究了带控制输入约束的二阶连续时间系统的包含控制问题。具有输入约束的一致性问题在文献[15-16]中也有研究。文献[17]分析了带有速度约束的二阶离散系统包含控制问题。文献[18]研究了带时滞和速度约束的离散时间多智能体系统的一致性问题。在此基础上，文献[19]解决了受速度和输入双重约束的二阶离散系统一致性问题。目前尚未见有关于带约束的采样系统包含控制研究结果。

本文研究了带有输入约束和有向切换拓扑的一阶采样多智能体系统的包含控制问题，提出了一种基于投影的分布式协调控制算法。首先为跟随者智能体设计了只需要利用自身和能直接通信的邻居智能体状态信息的分布式包含控制算法，接着将跟随者到领导者所形成的凸包的最大距离选择为Lyapunov函数，根据Lyapunov定理证明：在通信拓扑的并集中，只要每个跟随者智能体至少有一条从领导者到它的通信路径，Lyapunov函数最终能够收敛到0，也就是包含控制能够实现。

2 图论与预备知识

本部分列出必要的图论基础知识。通信拓扑图由G(V，E，A)表示，其中V=(1，2，3…n)表示顶点的集合。EV×V表示边的集合，加权邻接矩阵表示为A=[aij]n×n，aij代表边的权值，(j，i)E代表智能体i能收到智能体j的信息[20]。对于邻接矩阵A，如果(j，i)E，有aij＞0(i≠j)，否则aij=0。在有向图中，有序边序列(i1，i2)，(i2，i3)，…构成了图的有向路径，其中(ij，ij+1)V。令多个有向图G1，G2，G3，…，Gs的并集为Gz，Gz仍是一个有向图，且Gz的边集等于全部有向图Gz，j=1，2，3，…，s边集的并集。

定义1[19]：当x≠0时(0)=0，Uir是一个有界的非空封闭集合，且0Ui。此时(x)定义为。且，其中、均是正常数。即约束算符(x)的物理意义是找到一个方向相同的矢量x使得满足，并且对于任意μ[0，1]，都满足μ(x)Ui。需要特别指出的是，约束算符不要求Ui是凸性的(如图1约束算符举例所示)。

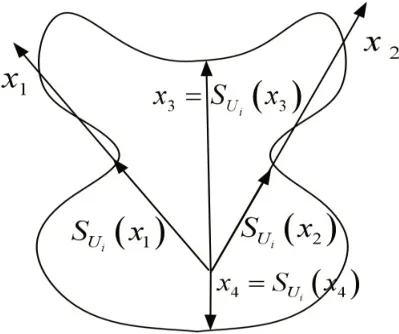
图1 约束算符举例

3 问题提出及系统设计

设多智能体系统由m+n个智能体组成，其中包括m个领导者和n个跟随者，跟随者由集合N={1，2，3，…，n}，领导者由M={n+1，n+2，n+3，…，n+m}表示，ri(k)h表示智能体的在kT时刻的位置，ui(k)h表示智能体在kT时刻的控制输入。在本文中我们只讨论h=1的情况。T＞0表示采样周期，后面我们用k表示kT。通信拓扑图G(kT)=G(V，E(kT)，A(kT))中每个智能体均为一个节点。

对于连续时间系统，则每个智能体的动力学模型可描述为：

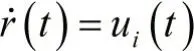
其中控制输入ui(t)依据采样数据变化，在一个采样周期[kT，(k+1)T]中，ui(t)为一个恒定的值。由此可得出一个周期内智能体的位置变换为：△r=ui(t)T。

考虑到每个智能体的输入受到非凸约束，其动力学方程可写为：

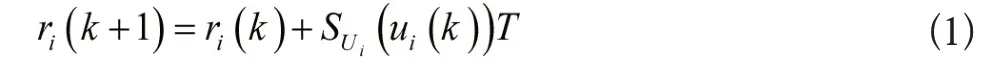
其中，rih是智能体的位置，uih是在时间段[kT，(k+1)T]智能体的控制输入。假设当k＜0时，有ri(k)=ri(0)。包含控制的目的是设计一种控制器，使得所有的智能体的控制输入约束在集合Ui中，且所有智能体都能进入到由领导者所构成的凸包Hi中。即，为了达到包含控制的效果将控制器定义为：

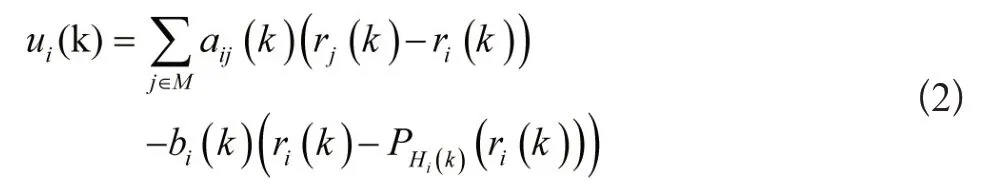
式中，aij(k)A(k)，A(k)是在kT时刻的加权邻接矩阵，如果跟随者能与任意领导者通信，则bi(k)＞σ，否则bi(k)=0，这里σ是一个正的常数。假设在满足aij＞0 的情况下，同样满足aij＞σ。Hi(k)Hi为智能体i能直接获取信息的区域。

定义如下变量：

当ui(k)=0 时，设ei(k)=1。显然0＜ei(k)≤1，由欧几里得范数定义可得：

将公式(4)与(1)结合得：

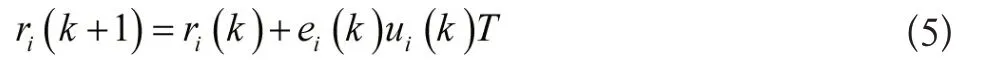
假设1：在kT时刻，通信拓扑图的并集中跟随者智能体与领导者之间至少存在一条有向的路径。

假设2：假设QmaxT＜1，Qmax为aij(k)+bi(k)的最大值，即

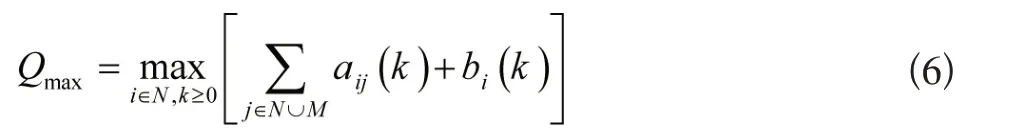
引理1[22]：设Yh，Y是一个非空闭合凸集。yi是h上的任意一个向量，且ai＞0，如果满足ai=1，i{1，2，3，…，n}，则有：。

将李雅普诺夫函数建立为：

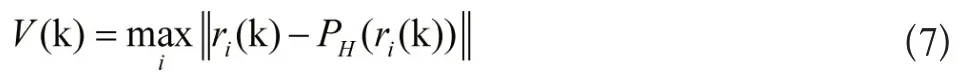
根据假设1、2，系统(1)的包含控制可由算法(2)实现，具体的的推理过程如下，由公式(1)与公式(2)可得：

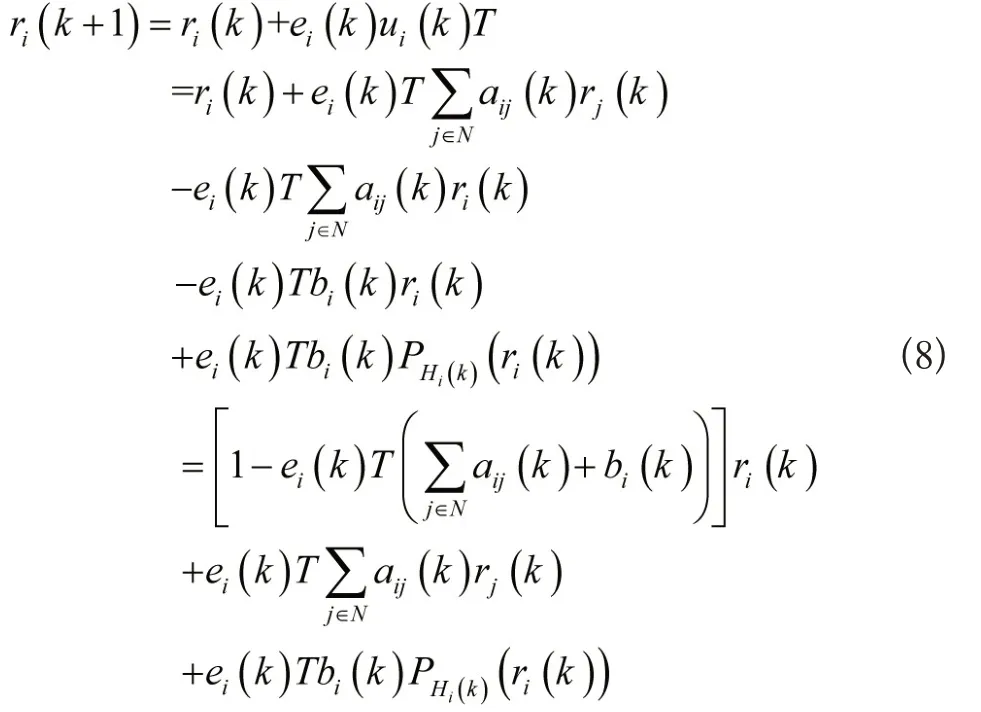
根据引理1可得：

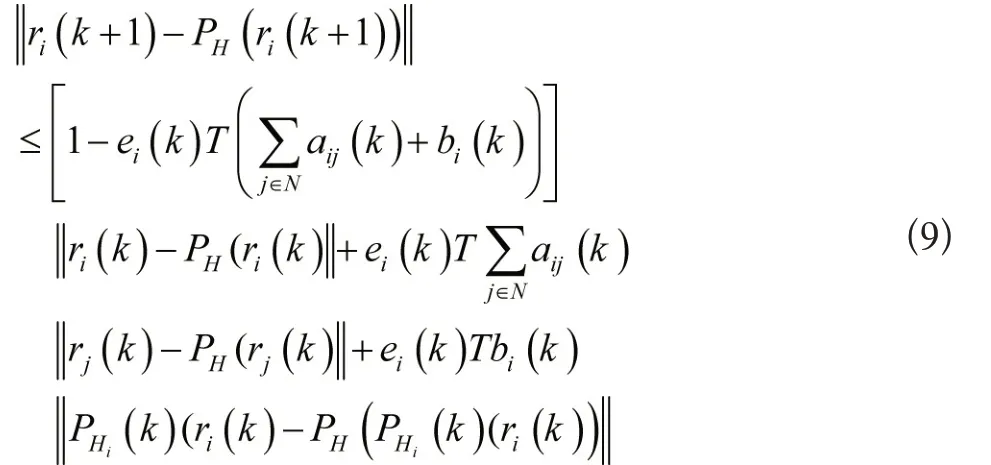
又Hi(k)H，可以得到，因此

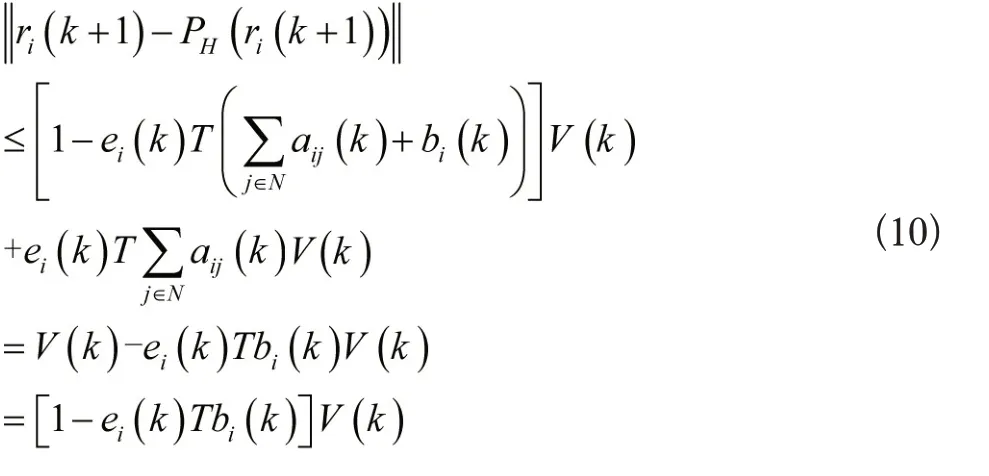
根据公式(6)和假设2可以得出0≤ei(k)Tbi(k)≤1，[1-ei(k)Tbi(k)]V(k)≤V(k)。由公式(9)(10)显然可以得出||ri(k+1)-PH(ri(k+1))||≤V(k)，因此V(k+1)≤V(k)，可得出V(k)为单调非增函数，这就表明智能体的位置与投影之间的最大距离随着时间的推移不会变大。为了实现最终的包含控制，需要证明limk→∞V(k)=0。分为两步来实现。

第一步：对于任意跟随者iN，当≥k，且0≤ψ1＜1，如果有，那么对于0＜ψ2＜1则有，根据公式(9)有：

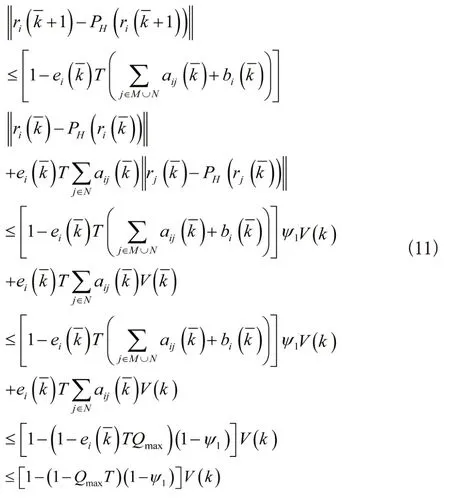
因此对于ψ2=1-(1-QmaxT)(1-ψ1)仍成立。

第二步：对于任意跟随者i2N，当＞0且对于k≥k和0≤ψi＜1时，有同时i2能接收到i1M N的信号，那么对于0＜ψ2＜1有。

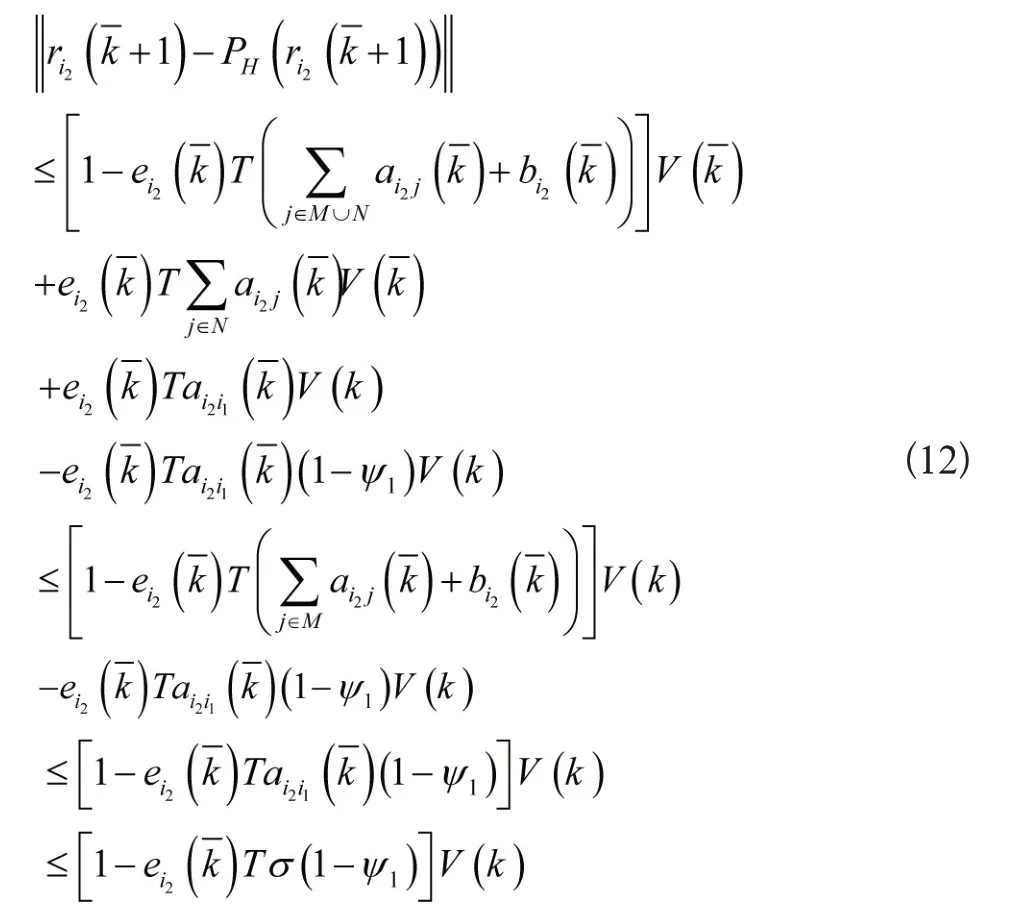
由公式(10)可得V(k+1)≤V(k)。根据假设1可得，在kT时刻必然存在至少一个智能体iqN能与领导者进行通信，同样也满足bi(k)＞σ。由上式可得，通过递归可得，此时C≥1且0＜＜1。同理，在kT时刻存在至少一个智能体ip≠iq能与领导者或者智能体iq进行通信，由第二步可得，对于任意0＜＜1均可得出，因此通过递归可得，此时C≥1 且0＜＜1。根据假设1，对于任意iN，存在一个有界整数＞0 使得，即，可得出limk→∞V(k)=0，即limk→∞=0。

4 数值仿真

在仿真中考虑由6 个智能体n1，n2，n3，n4，n5，n6 和4个领导者m1，m2，m3，m4构成的多智能体系统，包含控制的最终目标是所有智能体均能运到到由领导者构成的凸包中。多智能体系统的通信拓扑如图2所示，由三个拓扑结构G1，G2，G3组成，在系统运行过程中每隔1秒切换一次拓扑，显然G1∪G2∪G3满足假设1的条件。数值仿真中为了满足假设2，当aij(k)≠0且bi(k)≠0时，令，aij(k)=1．5，bi(k)=0．23采样时间T=0．2s。如图3所示，所有智能体的控制输入均约束在由半圆x2+(y-0．75)2=0．75(y≥0．75)和x2+(y+0．75)2=0．75(y≤0．75)与四条线段y=-x+1．5(0．75＜x≤1．5)、y=x-1．5(0．75＜x＜1．5)、y=-x-1．5(-0．75＞x≥-1．5)、y=x+1．5(-0．75＞x＞-1．5)围成的非凸区域中。智能体运动轨迹如图4所示，6个智能体初始位置不同，最后均能运动到由4 个领导者构成的凸包中。仿真结果表明全部智能体在控制器(2)的作用下能解决带输入约束的一阶采样多智能体系统包含控制题。

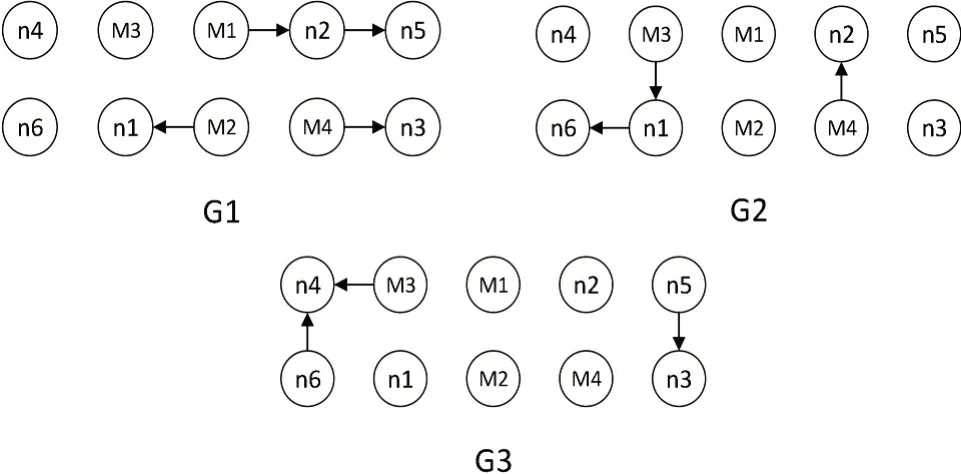
图2 多智能体系统通信拓扑

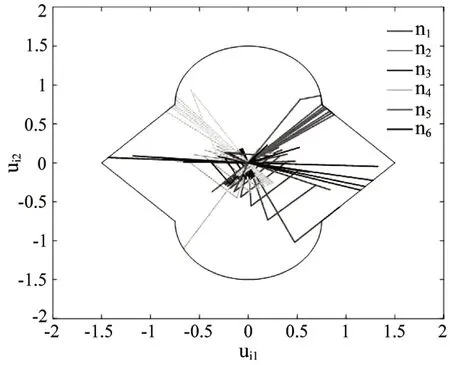
图3 智能体输入约束

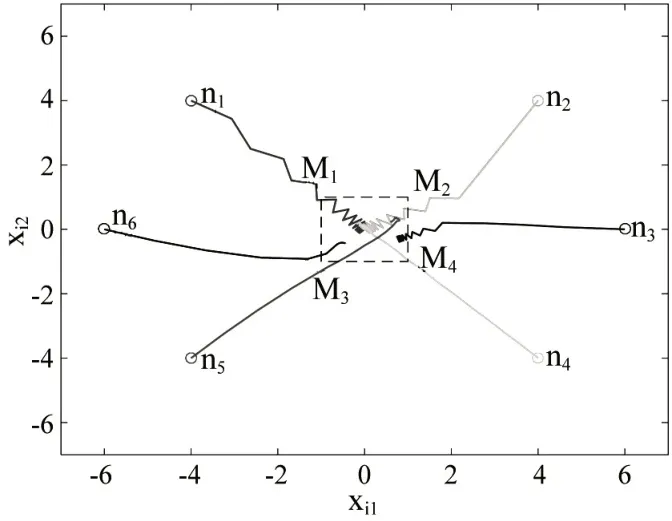
图4 智能体运动轨迹

5 结束语

本文研究了切换通信拓扑下带输入约束的一阶采样多智能体系统包含控制问题。首先针对跟随者智能体提出了基于投影算子的分布式包含控制算法，该算法只需要利用自身信息和能直接通信的邻居智能体或领导者信息。然后利用李亚普诺夫稳定性定理证明了在提出的控制算法的作用下跟随者智能体最终能保持在凸包以内。最后利用数据仿真证明了在拓扑图的并集中只要跟随者与领导者至少有一条通信路径的前提下提出的控制算法能解决具有输入约束的包含控制问题。下一步工作将探讨二阶采样多智能体受输入约束的问题。