自适应抗差CKF在舰载导弹武器初始对准中的应用

牟宏伟,韩 磊,李昂阳

（1．中国运载火箭技术研究院，北京 100076；2．首都航天机械有限公司，北京 100076）

1 引言

舰载导弹武器系统军事上得到了广泛应用。初始对准技术是导弹武器系统的关键技术之一，初始对准时间会影响发射控制流程时间，制约武器系统的快速反应能力，初始对准精度会影响导航初值误差，制约武器系统的精确打击能力。由于舰载发射平台面对的使用环境复杂且多变，常规的初始对准技术具有很大的局限性，导弹武器系统很难完成快速、高精度的初始对准。

捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)对导航结果的影响巨大[1-2]。初始对准则为在导航开始前确定载体初始姿态的过程，在很大程度上影响着惯性导航精度。SINS静基座初始对准通常采用标准卡尔曼滤波器(Kalman Filter，KF)，滤波模型采用小失准角假设下的线性误差模型。但是，在某些特殊场合，短时粗对准后，姿态误差可能并不满足小角度假设，此时基于线性模型假设的精对准很难收敛到对准极限精度或理想的对准精度。

因此，大方位失准角初始对准是SINS 的关键技术[3-4]。针对非线性误差模型的特点，目前基于Spherical-Radial Cubature 准则的容积卡尔曼滤波(CKF)应用较为广泛。该算法避免了非线性模型的线性化处理，弥补了EKF、UKF等传统非线性滤波算法的不足[4]。

但是，如果观测量存在粗差，且无法得到准确的噪声特性，会使得滤波估计性能受到了很大限制。针对上述问题，本文提出了自适应抗差CKF算法，能够有效提高滤波的稳定性和自适应能力，提高了舰载导弹武器系统的初始对准精度。

2 SINS大方位失准角误差模型

其中，sφi和cφi分别表示sin(φi)和cos(φi)(i=x，y，z)。

假设n'系相对于n系的角速度为，则欧拉平台误差角微分方程为：

2.1 误差方程

根据文献[1]，可得SINS姿态误差方程为：

速度误差方程为：

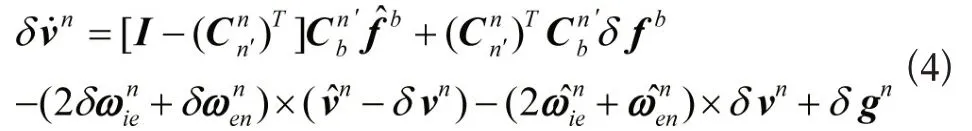
2.2 滤波模型

系统状态量为：

陀螺及加速度计的白噪声为：

其中，Gw为过程噪声输入阵，f(x(t)，t)和GW的描述见式(5)；h(t)为量测阵，且有h(t)=[02×3I2×202×5]；w(t)为过程噪声，v(t)为量测噪声，均服从高斯分布v(t)～N(0，R)。

3 抗差Kalman滤波算法

在初始对准中，粗差将对估计结果产生影响[4-5]。传统Kalman 滤波不能对粗差进行有效处理[4-6]，针对上述问题，本文利用抗差Kalman 滤波算法，并结合抗差估计理论，其中，稳健估计的研究更为成熟，较为实用的是稳健M 估计。本文在稳健M估计基础上，通过等价权原理，转化为最小二乘形式。如何选择权因子是抗差Kalman滤波的关键，本文采用权函数代替观测噪声协方差阵来减小或消除粗差的影响。

根据上述方式，参考文献[6]，假设原观测值权为Pi，则其等价权，权因子如下：

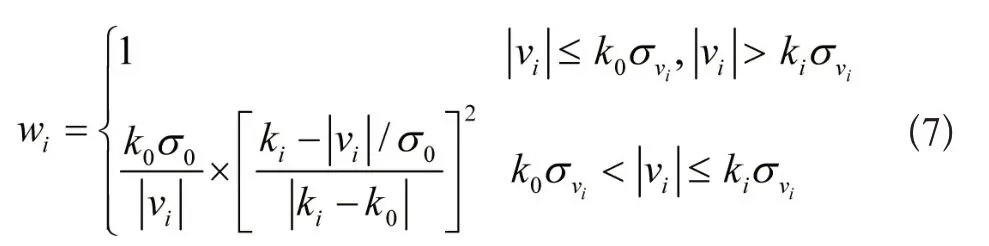
其中，vi为观测量Z的残差为vi的均方差，，为vi的权倒数；方差因子σ0可据得到；根据文献，一般选择k0与k1可分别取1．5～2．5，3．0～5．0。

4 自适应Kalman滤波算法

不准确的噪声特性通常会使滤波不稳定，甚至发散，因此，自适应滤波技术被广泛研究[6-9]。其中，Sage-Husa次优无偏极大后验(MAP)噪声估值器因计算简单、原理清晰等优点被广泛应用[10-11]。但是Sage-Husa 噪声估值器不能同时估计系统噪声和量测噪声，否则会导致滤波发散[11-13]。在实际环境中，量测噪声可由传感器的物理特性得到，但由于测量仪器精度、外界干扰等因素影响，系统噪声很难准确得到[14-16]。针对上述问题，结合协方差匹配判据，并引入自适应衰减因子，抑制消除自适应滤波的发散现象，提高了稳定性和自适应能力。

4.1 系统噪声估计方法

本文利用Sage-Husa对不准确的系统噪声qk和Qk进行估计，参考文献[9]，qk和Qk的公式如下：

其中，dk-1=(1-b)(1-bk)，一般选取0．95＜b＜0．99 为遗忘因子，为经验值，且b的取值越大，噪声统计变化较快。

4.2 滤波发散的抑制

Sage-Husa 估值器通常会出现发散现象，因此，参考文献[9]，本文同样利用协方差匹配判据，由式判断是否发散，如果发散则按照下式修正Pk/k-1，以抑制发散。其中，S≥1为可调系数为残差序列，即。

其中，0＜ρ≤1 为衰减系数，通常取0．95 左右，ρ的取值越大，越突出当前残差向量的影响。

5 自适应抗差CKF滤波算法研究

自适应抗差CKF可以同时兼顾观测粗差和系统噪声引起的误差，不仅能够克服观测粗差的影响，而且可以抑制系统噪声未知或时变引起滤波发散的问题。

假设非线性系统的状态方程和量测方程为：

其中，wk-1和vk为互不相关均值为零的高斯白噪声，且方差阵分别为Q和R。

在CKF滤波的基础上，结合上述自适应Kalman滤波和抗差Kalman滤波，可推导自适应抗差CKF算法如下：

(1) 计算容积点和权值

(2) 时间更新

(3) 量测更新

假设原观测值权为，则等价权。且有权因子：

发散判断：

根据式(28)判断发散，如果发散则按式(29)～式(32)修正Pk/k-1，不发散则进入下一步。

对于系统噪声不准确和观测粗差，自适应抗差CKF算法均有针对性的解决方法：由Sage-Husa自适应滤波在线估计系统噪声Qk，并抑制滤波发散现象；利用等价权系数调节观测噪声误差的影响程度，最终得到所需的最优和。

6 仿真研究

结合本文提出的自适应抗差CKF和SINS误差模型，滤波数值仿真条件如下。

系统状态初始估计值X(0)=0；初始失准角φx=φy=1°，φz=10°；初始速度误差为0．1m/s；陀螺仪常值漂移为0．02°/h，随机噪声为0．01°/h；加速度计零偏为1×10-4g，随机噪声为5×10-5g；GPS速度测量误差为0．1m/s；则初始方差阵P(0)、系统噪声阵Q和量测噪声阵R分别为：

P(0)=diag{(1°)2，(1°)2，(10°)2，(0．1m/s)2，(0．1m/s)2，

(0．02°/h)2，(0．02°/h)2，(0．02°/h)2，(100μg)2，(100μg)2}

Q=diag(0．01°/h)2，(0．01°/h)2，(0．01°/h)2，

(50μg)2，(50μg)2，0，0，0，0，0}

R=diag{(10m)2，(10m)2，(0．1m/s)2，(0．1m/s)2}

(1) 在某段时间内，速度观测量增加3m/s粗差，且增大滤波采样频率，分别比较CKF和抗差CKF两种非线性滤波方法，仿真时间300s。仿真结果见图1～图3。

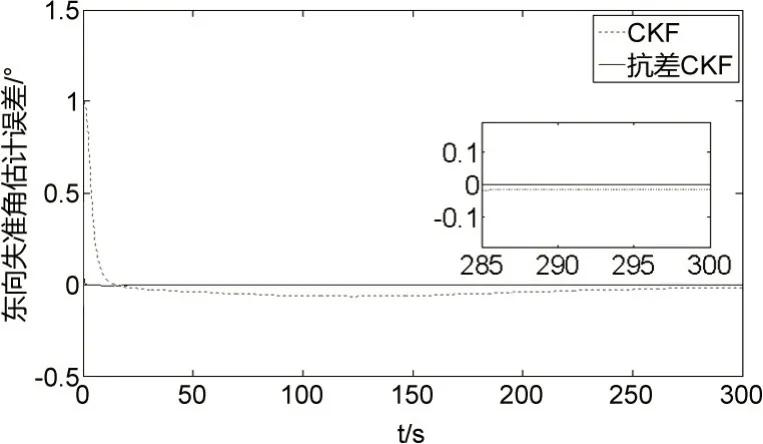
图1 东向失准角估计误差曲线

图3 方位失准角估计误差曲线

从图1、图2 和表1 可以看出，对水平失准角，抗差CKF估计精度更高，而且误差曲线相对平缓，收敛速度也较快；从图3 和表1 可以看出，对方位失准角，抗差CKF 估计精度和收敛速度优于CKF，而且没有较多的毛刺，滤波更稳定。

图2 北向失准角估计误差曲线

表1 基于CKF和抗差CKF的仿真结果

(2) 在仿真条件(1)的基础上，假设实际系统噪声为Q'=10Q，分别比较抗差CKF和自适应抗差CKF两种滤波方法，仿真时间300s。仿真结果见图4～图6。

图4 东向失准角估计误差曲线

图5 北向失准角估计误差曲线

图6 方位失准角估计误差曲线

从图4～图6和表2可以看出，两种滤波算法对东向失准角的估计精度差不多，对北向失准角和方位失准角的估计，自适应抗差CKF能够保持较高的估计性能。

表2 抗差CKF和自适应抗差CKF的仿真结果

7 试验验证

为了验证自适应抗差CKF滤波算法实际初始对准中的可行性，以某次SINS 实测数据为基础，进行离线分析，试验设备的安装见图7，基于自适应抗差CKF 滤波算法和CKF滤波算法的方位角对准结果见表3。

图7 试验设备安装图

表3 基于CKF和自适应抗差CKF的对准结果

从表3中的试验结果可知，自适应抗差CKF滤波算法的对准精度更高，很好地解决了量测信息异常或系统噪声特性不准确带来的误差，提高了初始对准精度。

表3 基于CKF和自适应抗差CKF的对准结果

8 结束语

本文研究了自适应抗差CKF 滤波算法，该算法可以同时兼顾观测粗差和系统噪声不准确引起的误差。通过数值仿真和实验验证，在观测信息异常或系统噪声特性未知的情况下，自适应抗差CKF 能够有效实现大方位失准角初始对准，提高了失准角的估计精度和收敛速度，增强了滤波算法的稳定性和自适应能力。