晃动基座下正向-正向回溯初始对准方法

徐 祥，徐大诚

(1. 苏州大学电子信息学院,苏州 215100；2. 苏州大学微纳传感技术研究中心,苏州 215100)

0 引 言

捷联惯性导航系统具有自主性高、隐蔽性好、数据更新率高等优点，成为舰船、车用、消费类电子等产品定姿、定速、定位的首选系统[1-4]。捷联惯性导航系统在进入导航定位之前，通常需要进行初始对准过程，以实现初始姿态角的获取。当前常用的初始对准过程可以分为“粗对准+精对准”模式以及非线性滤波的大方位失准角初始对准模型[5-8]。文献[9]提出了一种七阶正交容积卡尔曼滤波(Cubature quadrature kalman filter,CQKF)算法，实现了SINS大失准角初始对准。然而，采用非线性滤波方法进行大失准角条件下的初始对准时，会导致计算量大、滤波不稳定、收敛速度慢等问题，使得其在工程应用中受到限制[10]。因此，大量研究均围绕“粗对准+精对准”模式展开。

传统“粗对准+精对准”采用两个独立的过程进行，即粗对准过程主要完成未知姿态角的粗估计[11-12]。文献[2]提出了一种静基座上自对准方法，文献[7]实现了晃动基座上的粗对准过程。但这些方法都只是讨论了不同状态下的粗对准，无法实现姿态误差的最小化。因此，需要通过粗对准过程，建立小角度误差的导航系线性误差模型，再利用Kalman滤波实现姿态角的进一步估计，从而完成初始对准过程[13-14]。

近年来，随着计算机技术的不断进步，其存储容量和计算速度都得到了较快的发展，这也为基于回溯原理的快速初始对准奠定了基础[15-19]。但这些方法都只是在粗对准或精对准中分别进行回溯，没有充分将两者进行融合，使得存储过程冗余。另外，由于计算机在读取存储数据时，通常采用正向数据流形式，这使得传统正逆向回溯过程在实时算法设计时较为复杂。而且，正逆向导航需要存储所有时刻的惯性传感器数据，这导致对存储空间和计算速度要求较高，不利于快速对准的实现。基于传统正逆向导航回溯初始对准方法存在的问题，本文将在导航惯性系粗对准的基础上，提出一种基于导航惯性系误差模型的精对准方法，并利用时不变姿态误差估计方法，设计正向-正向回溯初始对准，解决传统回溯对准方法设计复杂度高、数据存储量大、计算效率低的问题，实现快速初始对准目标。

1 常用坐标系定义

为方便后续工作，基于正向-正向回溯原理的初始对准技术涉及到以下几个坐标系，分别定义为[3]：

1) 地心惯性坐标系(i系)：选取初始对准起始时刻地球系作为初始地心惯性系，并且不随地球运动而改变。

2) 导航坐标系(n系)：选取“东-北-天”方向为导航坐标系。

3) 导航惯性坐标系(n0系)：初始对准起始时刻导航坐标系，并且相对惯性系不变。

4) 载体坐标系(b系)：定义“右-前-上”为载体坐标系。

5) 载体惯性坐标系(b0系)：初始对准起始时刻载体坐标系，并且相对惯性系保持不变。

2 导航惯性系初始对准原理

为实现正向-正向回溯初始对准过程，本文将在n0系下建立系统误差模型，并以此模型设计滤波算法，实现回溯对准。初始对准过程将分为粗对准和精对准两部分。

2.1 导航惯性系粗对准

(1)

式中：

(2)

由惯导比力方程可知：

(3)

当载体处于晃动基座上时，可以假设载体无线速度运动，因此，式(3)可以采用矢量观测器表示

(4)

式中：

(5)

假设陀螺仪量测和加速度计量测表示为：

(6)

采用陀螺仪量测和加速度计量测构造矢量，可以得到

(7)

由式(2)可知：

(8)

由最优基姿态确定算法可知[16-17]：

(9)

2.2 导航惯性系精对准

为了得到更高的初始对准精度，通常在粗对准之后需要进行精对准。传统的初始对准方法中，精对准过程与粗对准过程通常互不相关，粗对准只为精对准提供一个粗略的姿态，精对准过程需要继续采样传感器输出,从而实现姿态误差的估计。这一过程中没有充分利用粗对准过程积累的有效数据，导致对准过程延长。同时，现代计算机的处理能力已能够在一个传感器采样周期内进行多个滤波环节的运算，若需要等待传感器采样更新才能进行一次姿态误差角估计更新，则大大浪费了计算机的处理速度，也延长了对准时间。因此，需要将粗对准与精对准进行融合，充分利用粗对准采集数据及计算机的处理能力，实现快速对准目的。

为实现这一过程，需要将传统的时变姿态误差角估计问题转变为时不变姿态误差角估计问题。因此，本文将对传统的导航系误差模型进行修改，设计导航惯性系误差模型，从而实现时不变姿态误差角估计。假设粗对准之后，方向余弦矩阵可以表示为

(10)

式中：

(11)

将式(11)代入式(10)可得

(12)

式(12)表示n0系下姿态误差与方向余弦的关系。令

(13)

则有

(14)

(15)

因此，n0系姿态误差角微分方程可以表示为

(16)

从式(16)可以看出，姿态误差角的变化只与陀螺仪量测误差有关，考虑到对准过程较短，且陀螺仪量测误差较小，可以近似认为姿态误差角为时不变量。由坐标变换关系可知

(17)

由晃动基座条件可知，vn=0，因此式(17)可以表示为

(18)

将式(3)代入式(18)，并忽略n系速度项可得

(19)

因此，n0系速度误差方程可以表示为

(20)

由式(16)和(20)可得n0系下系统误差模型

(21)

(22)

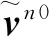
(23)

至此，基于n0系的初始对准模型建立完成。对上式(21)进行离散化，并采用Kalman滤波，即可实现时不变姿态误差角φn 0的估计，从而实现精对准。

3 正向-正向回溯初始对准原理

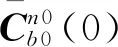
图1 正向-正向回溯对准结构图Fig.1 Structure diagram of forward-forward backtracking alignment method.

4 试验与结果

4.1 仿真试验

仿真硬件环境为Intel (R) Core(TM)T9600 CPU 2.80 GHz，4G RAM，Windows 7操作系统。利用Matlab profile功能对算法运行时间进行统计，检验算法的收敛速度。

表1 传感器误差设定Table 1 Sensor errors setting

仿真过程中，惯性传感器误差参数设定如表1所示。设定惯性传感器数据输出率为200 Hz。仿真过程模拟舰船系泊状态下初始对准，设定晃动参数如表2所示。

表2 摇摆参数设定Table 2 Swinging parameters setting

在上述仿真条件下，采用最优基方法进行300 s粗对准，并对粗对准数据进行记录，采用设定回溯过程为4次，得到对准误差曲线图如图2～4所示。图中点线表示第一次回溯结果、点画线表示第二次回溯结果、虚线表示第三次回溯结果、实线表示第四次回溯结果。

粗对准结束时刻航向对准精度为0.5°，水平对准误差为0.02°左右。当由粗对准进入回溯对准时，由于初始误差协方差矩阵P0|0为经验值，且通常设置为较大，导致在回溯起始阶段出现较大的调节现象。但经过两次回溯计算纵摇误差角可以收敛到0.006°左右，横摇误差角可以收敛在0.004°以内，航向误差角可以收敛在0.06°左右，达到了精对准的目标。同时，由于采用正向-正向回溯过程，不需要在回溯过程中进行大量IMU数据更新，使得算法可以在1.5 s内完成一次回溯计算，四次回溯过程计算时间为6 s。通过分析可以经过两次回溯之后算法即可达到极限精度，因此总的对准时间为303 s，这大大提高了初始对准的收敛速度，达到快速对准的目的。

图2 纵摇误差Fig.2 Curves of the errors of pitch

图3 横摇误差Fig.3 Curves of the errors of roll

图4 航向误差Fig.4 Curves of the errors of yaw

4.2 转台试验

在仿真试验的基础上，设计转台试验，检验算法在实时系统上的对准性能。转台试验实物图如图5所示。设定摇摆参数如表2所示，IMU数据更新频率为200 Hz。对准过程中，先进行300 s粗对准，然后进行四次回溯对准，并以转台输出为姿态基准，四次回溯对准过程误差曲线如图6、7和8所示。

从图6和7中可以看出，水平姿态角在一次回溯之后即可达到稳定值，纵摇角误差均值为-0.0007°，标准差为0.0156°，横摇角误差均值为0.0034°，标准差为0.0186°。航向角经过两次回溯也收敛到稳定值，对准误差均值为-0.057°，标准差为0.0077°。其中，一次回溯过程的计算时间为1.5 s，因此可以在303 s内完成初始对准过程，加速了对准的收敛速度，达到了快速对准的目的。

图5 转台实物图Fig.5 IMU and turntable

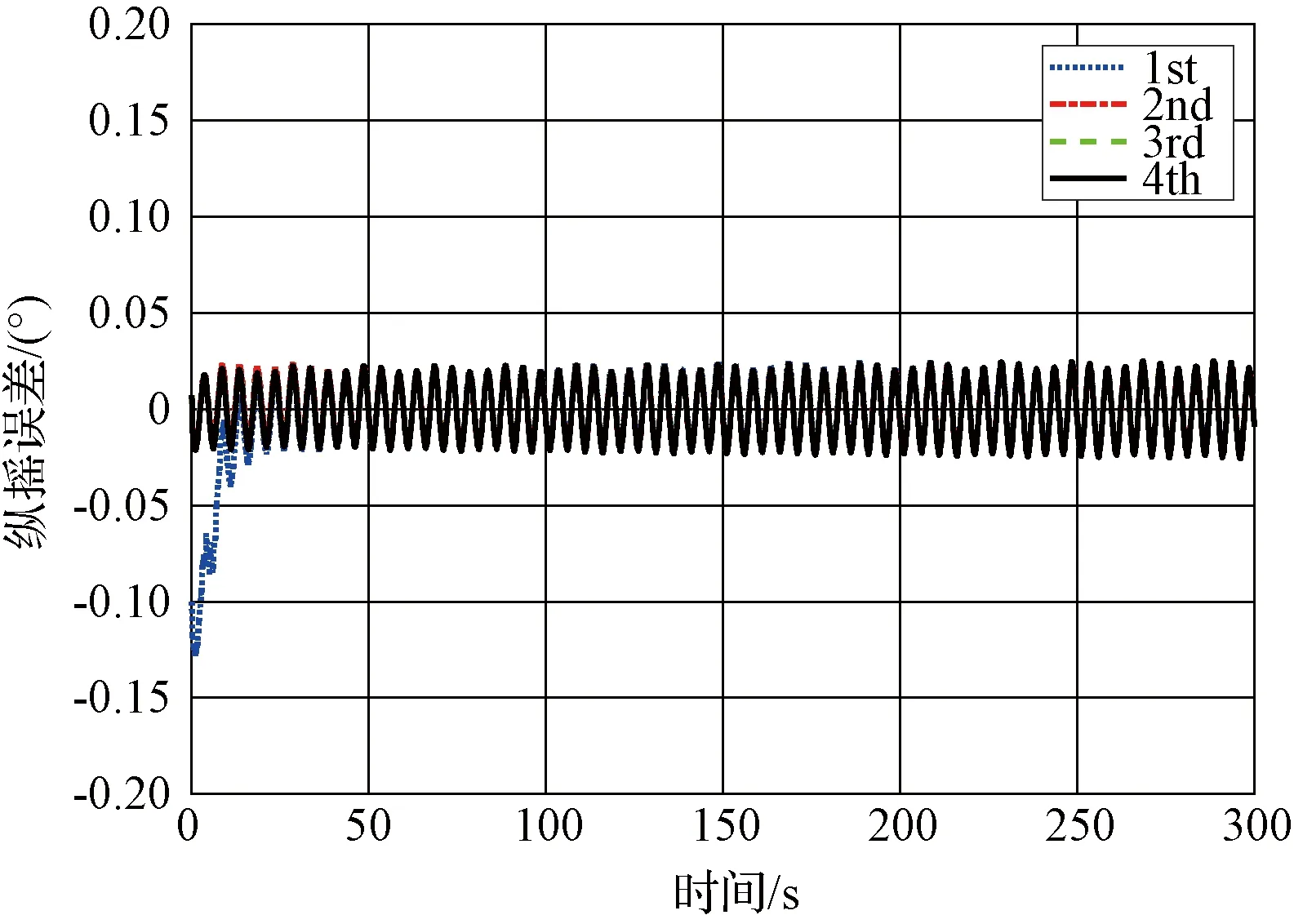
图6 纵摇误差Fig.6 Curves of the errors of pitch

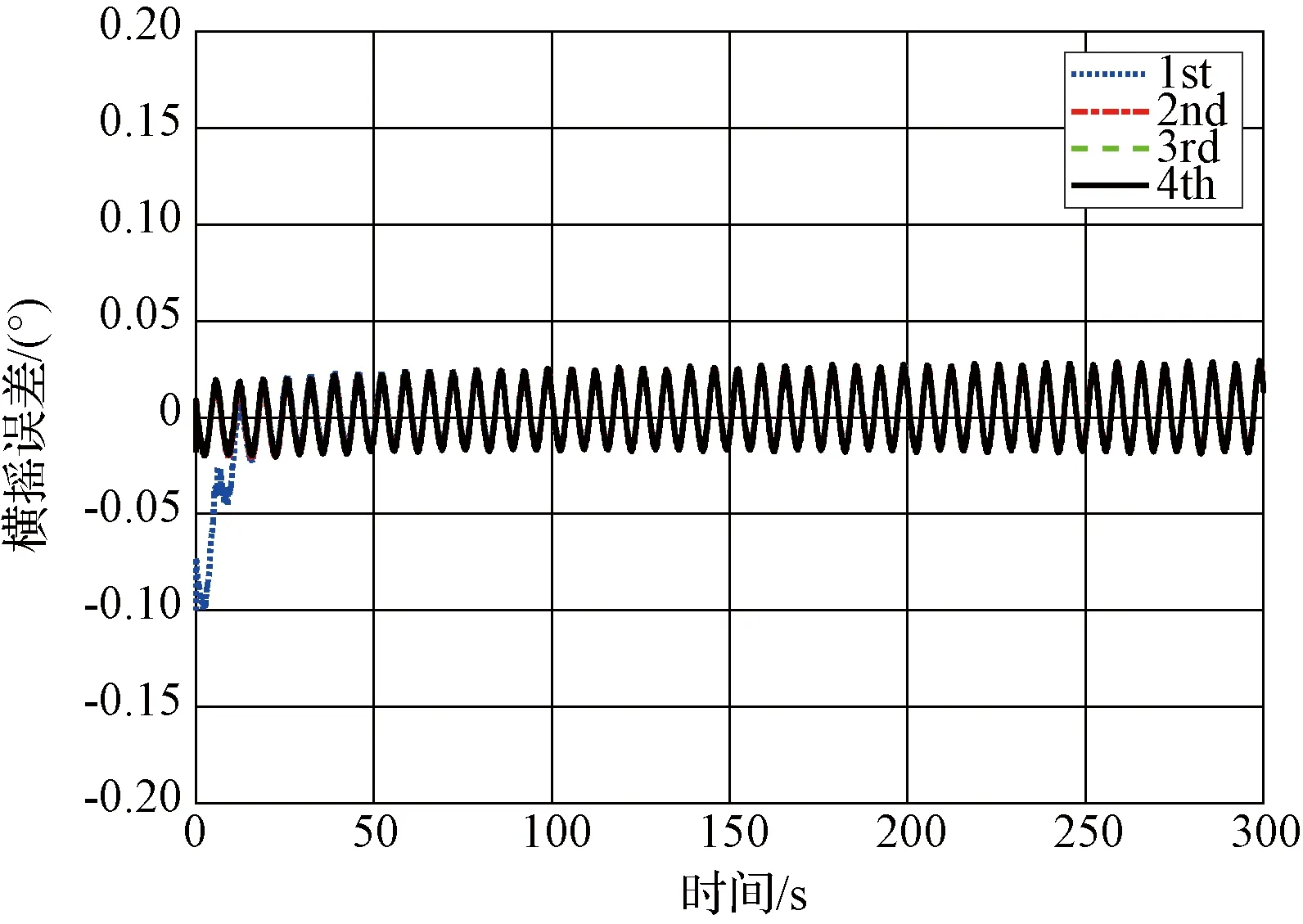
图7 横摇误差Fig.7 Curves of the errors of roll

图8 航向误差Fig.8 Curves of the errors of yaw

在转台试验中，由于转台数据是由惯导数据触发的，这使得转台数据在输出的时候相对于惯导数据存在延时现象，从而造成水平姿态误差波动较大。

5 结 论

针对初始对准收敛速度与收敛精度的矛盾问题，本文设计了一种正向-正向回溯初始对准方法，利用惯性系初始对准基本原理，构造了基于n0系的系统误差方程，实现了时变姿态估计到时不变姿态估计的转变，为正向-正向过程奠定了基础。通过设计仿真试验与转台试验，检验了正向-正向回溯对准在晃动基座上具有收敛速度快、对准精度高、计算效率高等优点，能够解决初始对准收敛速度与收敛精度矛盾的问题。