运载火箭主动段自适应增广控制

韦常柱，琚啸哲，何飞毅，潘 豪，徐世昊

(1. 哈尔滨工业大学航天工程系，哈尔滨 150001；2. 上海航天控制技术研究所，上海 200233；3. 北京航天自动控制研究所，北京 100854)

0 引 言

运载火箭主动段气动环境复杂，干扰和不确定性大，对其飞行过程进行高精度控制存在一定的难度。同时，为了提升火箭的运载能力，目前采用的降低结构质量设计方法，将使得箭体的弹性振动响应容易被激发，进而产生控制饱和，与此同时也将带来更为严格的结构承载能力约束，需要对大横、侧向载荷状态进行精细控制，以降低结构产生破坏的风险。

针对运载火箭的上述控制问题，目前国内外学者展开了深入的研究。Muse等[1]针对干扰、不确定性及未建模动态问题，设计了模型参考自适应控制器以提高标称PID控制的性能。常亚菲等[2]提出了基于神经网络特征模型的自适应滑模姿态控制方案，通过将对象模型中的非线性、时变不确定性压缩至特征参量，并结合模糊神经网络将快时变特征显式地表征在特征模型中，从而简化了自适应律的设计。钱默抒等[3]针对可重复使用运载火箭一子级再入垂直着陆阶段，考虑参数不确定性与外界有界干扰采用自适应滑模动态面控制策略，提升了姿态角跟踪能力。杨云飞等[4]通过建立包含发动机-伺服回路动力学模型的全箭动力学模型，给出了保证弹性模态稳定的谐振频率判据，并计算了保证全箭弹性模态稳定的负载频率边界值。孟中杰等[5]基于鲁棒H∞和LQR理论设计了高超声速飞行器纵向通道主动控制系统，以满足飞行器在弹性振动、参数大范围摄动等复杂情况下姿态精细控制需求。崔乃刚等[6]针对可重复使用运载器大姿态机动时弹性振动问题，设计了基于四元数的自抗扰控制器，同时对高阶振动项进行数字滤波幅值稳定控制。杨伟奇等[7]针对火箭在强风干扰飞行段结构载荷过大的问题，研究了基于自抗扰控制方法的主动减载技术，并在考虑弹性振动条件下与传统加表反馈、攻角反馈主动减载[8]方法进行了对比，结果表明能够提高运载火箭的减载能力。

当前大多数研究成果在解决运载火箭飞行过程中某一种特定问题时具有较好的效果，但是当面对强干扰、大不确定性及多约束等多种复杂影响共同作用时，无法保证能够达到既定的高品质控制性能要求。为了应对上述多种因素同时作用下的综合影响，通常可将PID控制、校正网络以及加表反馈主动减载相结合，并通过对各参数的分析，权衡其在应对干扰、不确定性、弹性振动和结构载荷方面的控制能力，进而得出一套较为保守的控制参数[9]。为了进一步提高综合控制性能，充分发挥控制系统应对复杂飞行条件的能力，美国NASA提出了一种自适应增广控制方法[10]，其主要特点是：当运载火箭飞行过程中各类干扰和不确定性较小时，不对标称控制器进行调整；而当某一干扰因素过大时，控制系统能够最大化抑制该因素的影响；当各种干扰均较大时，通过自适应调整能够保证运载火箭在各干扰的作用下安全飞行。经过数年的发展，自适应增广控制方法从提出开始，经历了仿真校验[11-12]、飞行测试[13-14]和控制结构更新[15]等过程，同时一些学者对其性能进行了理论分析，如Angelov等[15]通过非线性系统的描述函数法在频域上分析了该方法中自适应律的非线性特性及其参数整定的部分依据。

上述学者的研究主要集中于对运载火箭主动段某一干扰情况下自适应增广控制方法的性能分析，而缺乏对该方法在外界复杂干扰、不确定性和大范围弹振频率变化下的作用机理研究，也没有给出增益自适应变化范围的设计方法，且未将自适应增广控制方法与干扰补偿和主动减载方法有机地结合起来进行综合研究分析。

本文针对运载火箭主动段将受到的强干扰、大不确定性、弹性振动变化及高结构载荷综合影响的问题，研究自适应增广控制系统综合设计方法，及包括标称PID控制、数字滤波器、自适应增益调整、干扰补偿与主动减载模块在内的自适应增广子系统在应对运载火箭主动段复杂控制问题时的整体性能，并着重进行了数字滤波器参数的优化设计，以及对自适应增益调整算法设计原理的深入研究和分析。

1 运载火箭纵向运动模型

由于运载火箭纵向运动受到的影响较为明显且具有代表性，本文仅针对纵向运动进行研究。首先不考虑刚体-弹性耦合作用，其动力学模型可用如下的传递函数进行表示：

(1)

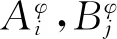
纵向弹性振动方程采用如下的简化形式来描述：

(2)

弹性振动作用下传感器测量方程为：

(3)

2 自适应增广控制系统综合分析

自适应增广控制是一种对运载火箭主动段复杂飞行环境下控制问题的综合处理方法，该方法对应的系统结构如图1所示。

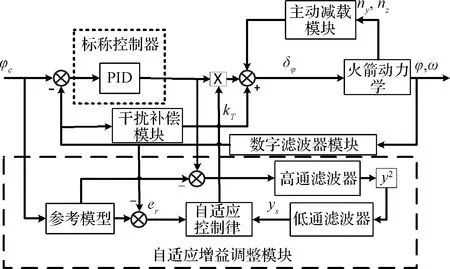
图1 自适应增广控制系统结构关系图Fig.1 Structure of the AAC system

由图1可知，自适应增广控制方法采用模块增广设计的思想，将运载火箭上升段的控制系统分为若干模块，包括：标称PID控制器模块、校正网络模块、自适应增益调整模块、干扰补偿模块、主动减载模块。其中:1)标称PID控制器模块主要实现标称飞行条件下的稳定控制；2)数字滤波器模块主要通过相位稳定和幅值稳定抑制弹性振动影响；3)自适应增益调整模块主要通过在线提高或降低控制器增益，以应对强干扰和大不确定性造成的较大姿态误差，以及飞行过程中弹性振动频率大范围变化导致滤波抑制效果不佳情况；4)干扰补偿模块主要用于提供补偿控制指令以提高控制器增益降低时姿态角控制精度；5)主动减载模块主要通过主动减载控制算法减小运载火箭在大动压区受到的横、侧向载荷。

3 运载火箭标称控制器与弹性振动优化数字滤波器设计

标称控制器采用经典的频域方法进行设计[8]，并通过增加数字滤波器以抑制弹性振动的影响。以俯仰通道为例，标称控制器结构如图2所示。

图2 标称控制器结构Fig.2 Structure of the standard PID controller

通过调节KP,KI与KD，使控制系统在标称状态下具有一定的幅值裕度和相位裕度。参考相关文献，取标称状态下幅值裕度为8 dB，相位裕度为35°[7]。

数字滤波器主要针对火箭飞行过程中弹性振动频率大范围变化的问题，考虑到传统固定参数滤波器的设计无法满足飞行全程弹性振动控制的需求，因此将运载火箭飞行段按时间划分为多个区间，在每个区间内分别优化设计滤波器。在第j个区间[tj,tj+1]内，对于第i阶弹性振动，可采用具有如下传递函数形式的滤波器进行控制：

(4)

将以对三阶弹性振动进行控制为例研究相应的滤波器优化设计方法。对于一阶弹性振动，其频率与运载火箭刚体控制频率较为接近，因此需设计滤波器实现相位稳定控制；而对于二、三阶弹性振动，其频率远大于刚体控制频率，但振动幅值较大，因此可设计滤波器实现幅值稳定。

针对三阶弹性振动的滤波器传递函数如下：

(5)

式中待设计的参数为ωi1,ωi2,ζi1,ζi2,kf(i=1,2,3)。

取运载火箭主动飞行段的第85 s特征点为例进行分析。在加入滤波器之前，标称控制器对三阶弹性振动的频率响应如图3所示。

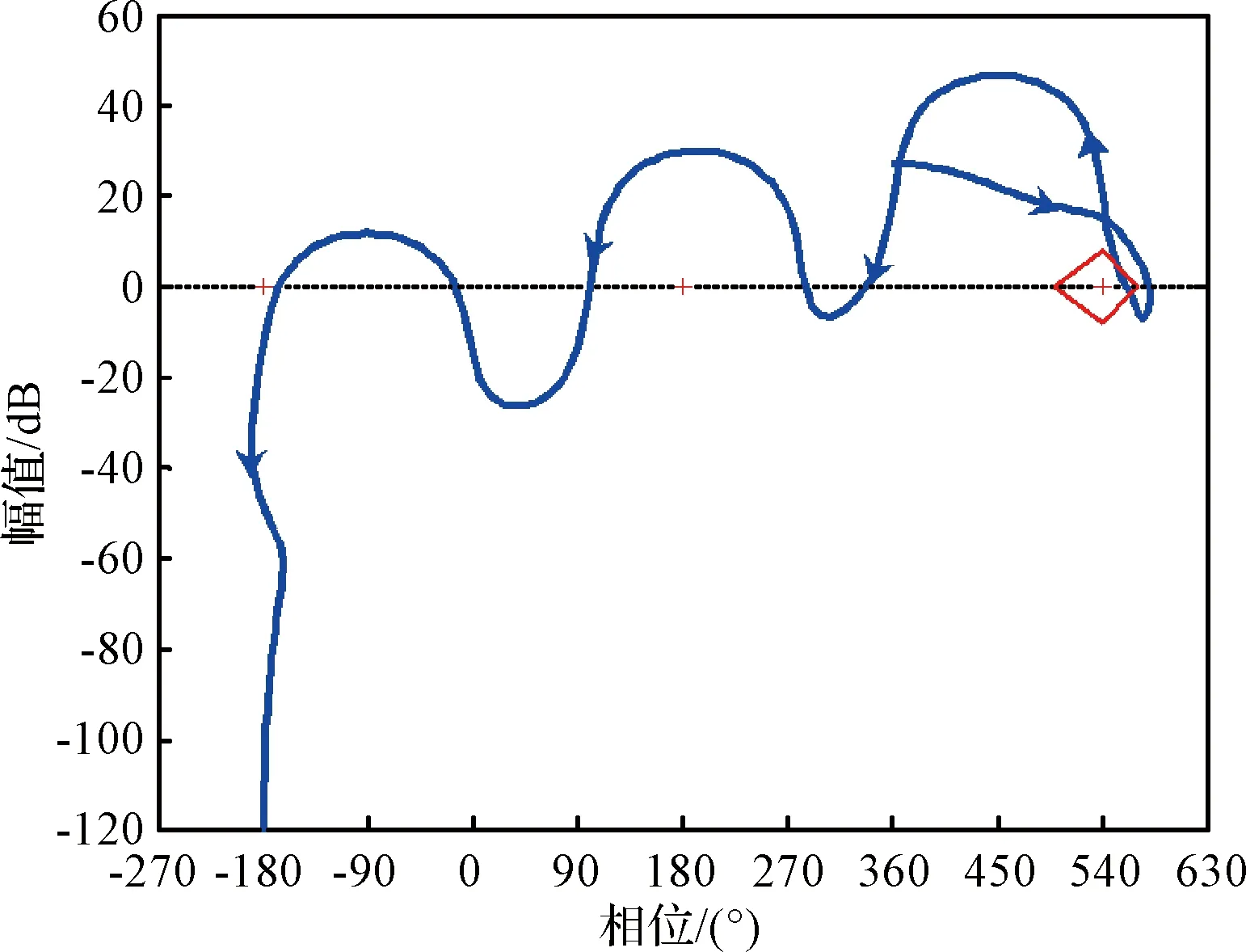
图3 加入滤波器前系统频率响应Fig.3 Frequency response of control system without filter

由图3可知，在开环幅频特性大于0 dB的所有频段内，幅相特性曲线的正负穿越次数之差(-1次)与系统开环传递函数正实部极点个数(2个)的一半不等，所以加入滤波器之前系统是不稳定的，需设计合理的数字滤波器以实现弹性振动的稳定。

考虑到数字滤波器的加入需在实现弹性振动稳定的同时，尽可能地保证刚体系统的控制性能，因此可将滤波器的参数设计问题转化为如下的多约束参数优化问题：

1)设计目标：加入数字滤波器后，系统刚体幅值裕度仍为8 dB，相位裕度仍为35°。

2)约束条件：

(1)为防止系统频率响应在第一次穿越540°(频率为ωg1)时幅值过小，导致其在干扰和偏差作用影响下进入临界稳定甚至不稳定区域，将该点幅值设置为大于8 dB。

(2)为了实现对一阶弹性振动的相位稳定，系统频率响应在第二次穿越0 dB(频率为ωc2)时的相位与540°的距离大于40°，第三次穿越0 dB(频率为ωc3)的相位与180°的距离大于40°。

(3)为了实现二、三阶弹性振动的幅值稳定，系统在二、三阶弹性振动(频率为ω2,ω3)处响应幅值小于-8 dB。

为了进一步提高优化效率，依据传统数字滤波器的设计经验，限制各参数的范围以减小搜索空间。对于ζi1,ζi2(i=1,2,3)，通常其值大小不会超过1，同时为防止陷波深度过大，其值不会小于0.01；而对于各级滤波器的角频率ωi1,ωi2(i=1,2,3)，其搜索范围应包含该级校正网络对应的弹性振动频率，并限制在刚体第二次相位穿越频率与各阶弹性振动频率的范围之间[16]。

综上所述，可得如下的优化模型：

s.t.

(6)

式中:ωc1为剪切频率，ωg2为穿越频率，ωc为刚体第二次相位穿越频率。本文采用粒子群优化方法对上述滤波器参数优化设计问题进行求解。

考虑三阶弹性振动频率分别为9.42 rad/s，21.99 rad/s和34.55 rad/s，在第85 s特征点处设计数字滤波器，经过迭代后得到最终的滤波器参数为：

由图4可知，所设计的滤波器在刚体截止频率(1.97 rad/s)范围内对系统幅值影响较小，且相位下降较为缓慢；在一阶弹性振动频率(9.42 rad/s)附近幅值下降较小，但相位迅速减小，使系统响应在一阶弹性振动幅值大于0 dB的部分之前相位提前穿越540°，进而实现一阶弹性振动的相位稳定；在二、三阶弹性振动频率(21.99 rad/s和34.55 rad/s)附近，滤波器幅值下降很大，使二、三阶振动幅值迅速下降，进而达到幅值稳定的目的。

图4 滤波器频域响应Fig.4 Frequency response of the filter

在加入所设计的滤波器后，系统频域响应如图5所示。由图5可知，在加入滤波器后控制系统实现了对一阶弹性振动的相位稳定和二、三阶弹性振动的幅值稳定，满足Nyquist稳定判据，因而系统是稳定的。

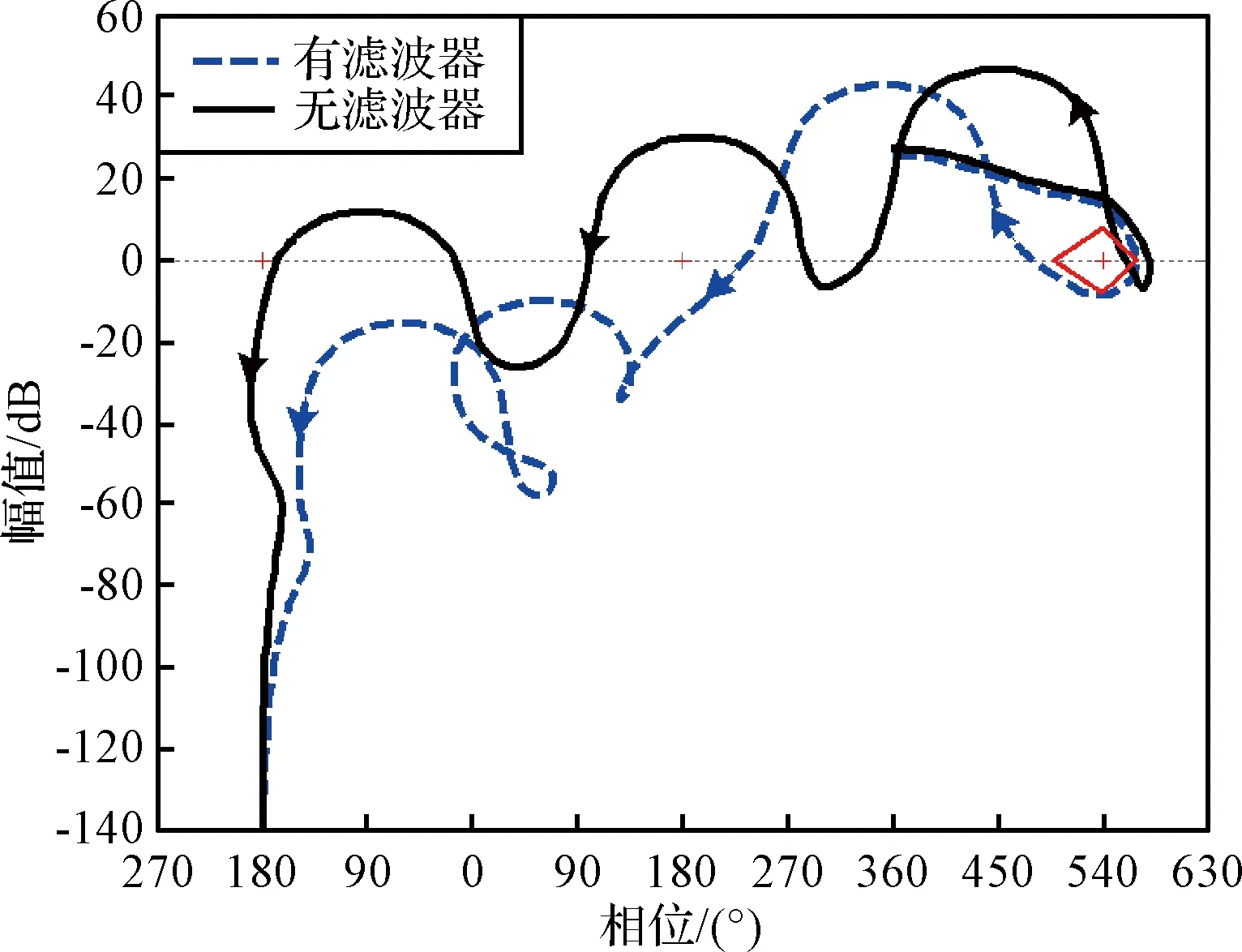
图5 加入滤波器前后控制系统频域响应Fig.5 Frequency response of control system with filter

基于上述方法，可以对主动段的所有特征点进行数字滤波器参数的优化设计，从而实现对大范围变化的弹性振动的有效控制。

4 自适应增益调整

针对运载火箭主动段受大范围干扰、不确定性，以及在数字滤波器切换过程中弹性振动影响明显的问题，通过自适应增益在线调整以充分发挥控制系统应对复杂飞行条件的能力，本文设计的自适应增益调整算法结构示意图如图6所示。

图6 自适应增益调整算法结构图Fig.6 Structure of the adaptive gain algorithm

由图6可知，本文所设计的自适应增益调整算法可表示为：

(7)

式中：er为参考模型与实际模型输出姿态角的偏差，ys表征弹性振动信号对控制系统的影响，kT为前向总增益。

自适应增益在线调整系统主要由参考模型、高低通滤波器及自适应律三部分组成，下面对各部分的原理及特性进行详细阐述。

4.1 参考模型

参考模型主要是对运载火箭在标称条件下的刚体受控运动进行描述，并通过设计模型参数形成期望跟踪指令，进而与实际运载火箭受扰动运动的姿态响应作差生成姿态角偏差，作为自适应律的输入，以达到在线提高PID控制器增益的目的。

参考模型的结构如图7所示。

图7 参考模型结构Fig.7 Structure of the reference model

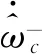
(8)

(9)

则可得到：

(10)

则参考模型可由二阶系统传递函数形式进行描述：

(11)

进一步，考虑到制导指令延迟、执行机构和传感器等寄生动力学环节造成的相位滞后因素，引入延迟环节e-τs，得到最终的参考模型如下所示：

(12)

式中:延迟时间τ需依据实际系统中执行机构、传感器与制导指令延迟等具体特性进行设计，用于匹配由于附加动力学导致的参考模型与实际模型之间的相位延迟[11]。

4.2 高低通滤波器

高通滤波器和低通滤波器的作用是提取并处理控制指令中由弹性振动激励产生的附加信号，并将其用于降低控制器增益。其结构如图8所示。

图8 高低通滤波器结构Fig.8 Structure of the high and low pass filter

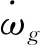
低通滤波器输出ys的表达式如下：

(13)

式中:Ghp(s)为高通滤波器的传递函数，Glp(s)为低通滤波器的传递函数。

高通滤波器的传递函数为：

Ghp(s)=s/(s+ωhp)

(14)

低通滤波器的传递函数为：

Glp(s)=ωlp/(s+ωlp)

(15)

式中:ωhp和ωlp分别代表为高、低通滤波器的截止频率。

由于需要获取控制指令信号中的弹性振动激励信号，因此ωhp取值稍高于运载火箭刚体控制频率。该信号取平方后通过低通滤波器获取信号中的低频成分，因此低通滤波器截止频率ωlp应取在刚体控制频率附近。

4.3 自适应律

综上分析可知，自适应律设计过程中主要考虑的因素为实际输出与参考模型输出之间的偏差，以及弹性振动的影响，其具体形式如下所示[15]：

(16)

式中:ka为自适应增益，ka,max为自适应增益最大值，kT,max,kT,min为前向增益最大值和最小值，Ke为自适应偏差增益，Ks为控制指令抑制增益，Kβ为自适应增益收敛系数。

4.3.1自适应律特性分析

当标称控制器稳定时，自适应律应用在运载火箭上升段时将出现以下3种工作状态：

1)当弹性振动影响较小时，即数字滤波器在各飞行段对弹性振动抑制效果较好，同时考虑到Kβ很小(因此可将其忽略)，则自适应律变为：

(17)

对式(17)进行拉氏变换可得：

(18)

由终值定理可得：

(19)

由式(19)可知，当参考模型与实际模型输出姿态角的偏差er不为0时，自适应增益ka将逐渐增大，最终收敛至ka,max。

2)当弹性振动影响明显时，这种情况主要出现在运载火箭进入大动压区横/侧向载荷较大，助推器分离、级间分离等结构变化明显或各飞行段数字滤波器进行切换时。同样忽略式(16)第1式中Kβ，则自适应律变为：

(20)

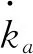
3)当运载火箭姿态得到稳定控制，且弹性振动影响较小时，实际模型与参考模型之间姿态角偏差er以及由于弹性振动引起的控制信号误差ys接近0，此时有

(21)

可以看出，当t→∞时，有

(22)

由式(16)可知，当t→∞时，kT=ka+kT,min=1，说明此时标称PID控制器能够很好地对火箭进行控制，因而自适应律对标称控制器无影响。

4.3.2增益上下限分析

在第3节中所设计的数字滤波器能够抑制弹性振动的影响，使系统性能满足稳定裕度的要求，因此只需考虑在使用标称控制器进行刚体控制时，控制器增益kT的变化范围。

增益上限的研究方法：对干扰、不确定性作用下的控制系统进行频域分析，确定其幅值裕度变化范围，并通过与标称控制器的幅值裕度对比，选取系统到达幅值裕度为0状态下的增益作为增益上限值。

假设质量偏差、推力偏差、气动偏差、密度偏差、质心偏差和转动惯量偏差在20 %内均匀分布，在不改变控制器前向增益kT的情况下对其进行蒙特卡洛仿真，得到幅值裕度分布如图9所示。由图9可知，在20 %偏差作用下系统最小幅值裕度为6.313 dB,最大幅值裕度为17.09 dB。则增益上限kT,max可通过解方程20lg(kT,max)=6.313求得，其值为2.0685。

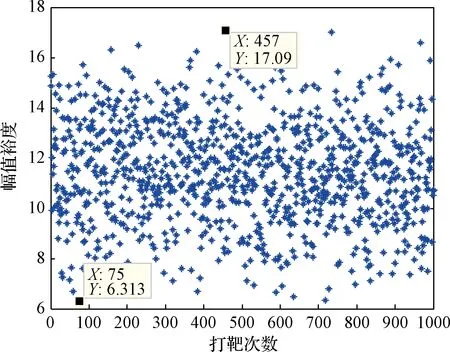
图9 20%偏差下控制系统幅值裕度分布Fig.9 Magnitude margin of control system with 20% perturbation

增益下限的研究方法：考虑到当弹性振动影响明显时，控制器增益kT在自适应调整算法的作用下将降低，进而导致系统的相位裕度减小。本文选定系统允许的最小相位裕度为20°，通过减小kT进行分析，系统相位裕度达到20°时所对应的控制器增益即为kT,min，此时系统频域响应如图10所示。图中，系统相位裕度为20°，幅值裕度为21.9 dB，系统稳定，此时kT,min=0.2925。

图10 增益下降至下限时系统频域响应Fig.10 Frequency response of control system with minus gain

综上所述，kT的变化范围在0.2925～2.0685之间，当干扰、偏差较大时，kT将在1～2.0685间变化，而弹性振动影响明显时，kT将在0.2925～1之间变化。

5 自适应增广控制系统仿真分析

本文干扰补偿采用扩张状态观测器精确观测扰动并进行控制补偿，主动减载则基于Lyapunov定理计算减载控制指令，并设置权重函数以保证姿态控制指令与减载控制指令之间的平滑切换[17]。姿态控制指令权重函数设置为：

(23)

式中:b>0,t1,t2确定了进行减载控制的时间窗口，将其设计为运载火箭动压较大的时间区域。

仿真条件设置如下：1)质量、推力、气动、密度、质心和转动惯量20%正向偏差。

2)加入风场模型。

3)分别在30 s跨声速和65 s大动压处设置数字滤波器，并在第50 s时进行切换。

4)采用的标称PID控制参数如表1所示。

表1 标称PID控制器参数Table 1 Parameters of nominal PID controller

6)高、低通滤波器参数：ωhp=8 rad/s,ωlp=4 rad/s。

7)自适应律参数：kT,max=2.0685,kT,min=0.2925,Kα=1000,Ks=100000,Kβ=0.02。

8)当kT小于0.8时，干扰补偿控制开始起作用。

9)采用主动减载后，减载时间窗口设置为62.5～72.5 s，切换函数中b=2.4。

仿真结果如图11～图15所示，其中PID表示标称控制器，AAC表示增益自适应调节律，DOC表示干扰补偿，LR为主动减载。

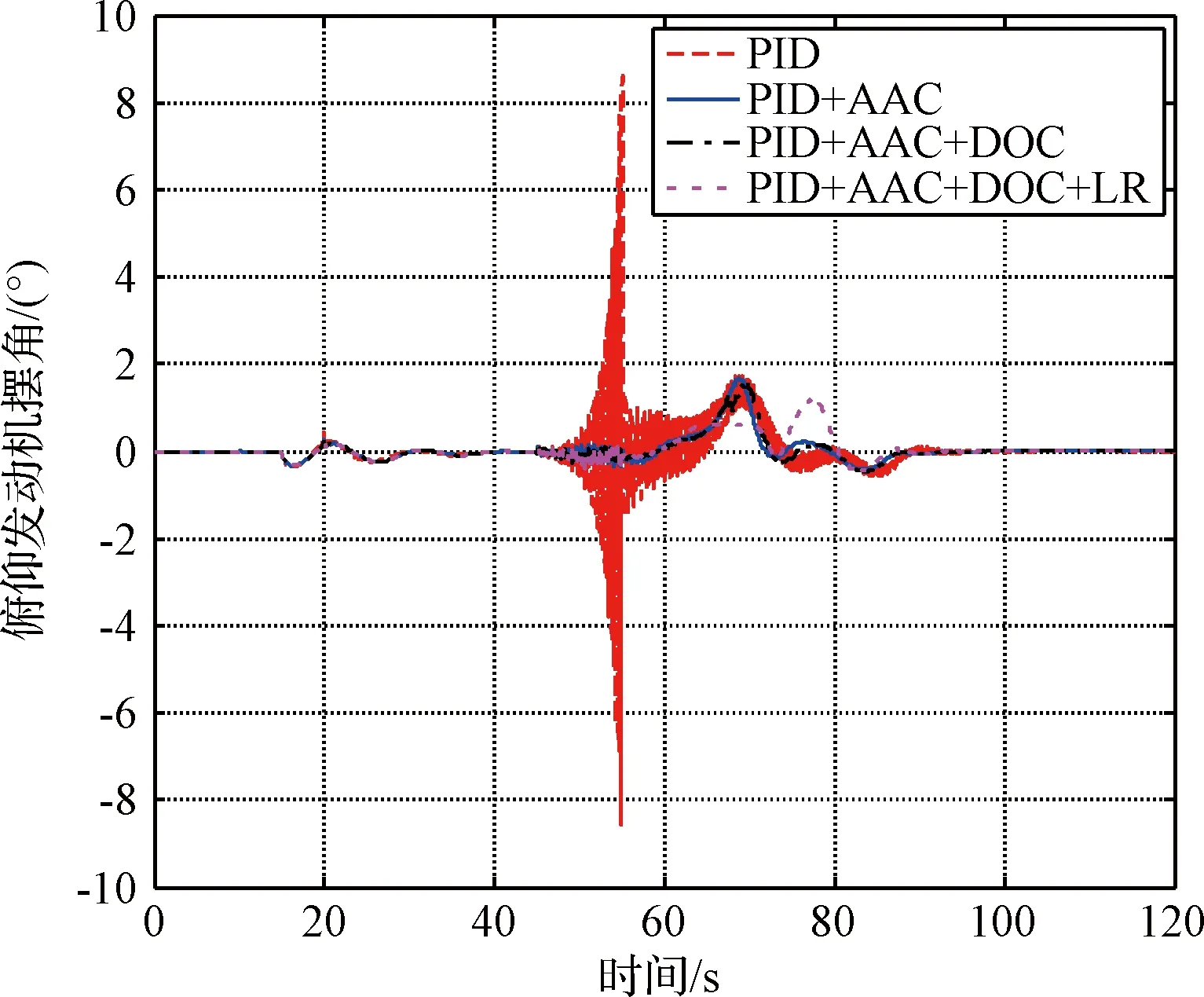
图11 俯仰发动机摆角曲线Fig.11 The swing angle curve of pitch engine

图12 控制增益变化曲线Fig.12 Curve of the adaptive gain

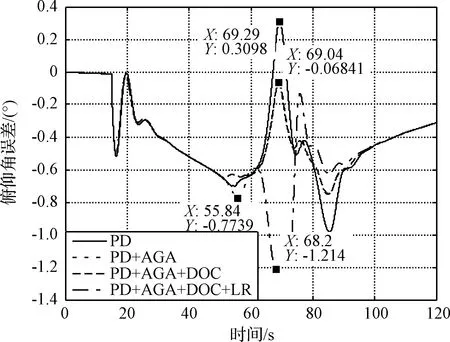
图13 俯仰角误差曲线Fig.13 Curve of the pitch angle error

图14 气动弯矩变化曲线Fig.14 Curve of pneumatic bending moment

由图11可知，在50～60 s飞行段，由于数字滤波器切换导致弹性振动影响突然增大，加入自适应增益调整的控制器相比于单一的PID控制器，其发动机摆角振动幅值从8°减小到小于0.5°。但随着控制增益的下降(见图12)，俯仰角误差增大到约-0.77°，而加入干扰补偿控制可显著降低误差至约-0.6°。可见相较于传统PID方法，AAC的引入能够在线降低滤波器切换所致弹性振动变化明显阶段(50～60 s)的增益，以减弱弹性振动对控制指令带来的影响，但控制增益的降低会在一定程度上增大俯仰角误差，此时为保证控制精度则需引入干扰补偿模块(DOC)以产生补偿控制指令。综上可见，控制系统在AAC与DOC的综合作用下，具有更强的抑制振动影响及抗扰能力。

图14可知，在62～72 s加入主动减载后，使火箭所受的气动弯矩最大值由未加入主动减载时的约250 kPa·rad减小为约200 kPa·rad，减小约20%。当不采用切换函数，硬切换姿态控制指令与减载控制指令时，俯仰角误差曲线如图15所示。

图15 俯仰角误差曲线对比Fig.15 The contrast curve of pitch angle error

由图15可知，切换函数的加入可快速、平滑地切换两种控制指令，实现了姿态控制与主动减载之间的均衡，避免了硬切换导致姿态角误差陡增的问题。

6 结 论

本文针对运载火箭上升段受到大偏差、干扰和大范围弹性振动变化影响的复杂控制问题，研究了基于自适应增益调整与模块增广构架的自适应增广控制方法：通过增益在线自适应调节提升火箭在大偏差、弹性振动影响下的控制品质；自适应滤波器能够有效控制弹性振动的影响；干扰补偿控制器可对干扰进行精确观测并加以补偿，以提高控制增益降低时的控制精度；主动减载控制器能够在运载火箭经过大动压区时控制攻角与侧滑角以有效降低气动载荷。

本文的研究对于目前运载火箭主动段复杂控制问题的解决，及未来新一代运载火箭控制技术的发展均具有理论研究意义和工程应用价值。