负反馈放大电路的稳定性分析与设计
2022-07-30 06:24赵春艳周小燕梁青青
电气电子教学学报 2022年3期
赵春艳 周小燕 梁青青
(兰州文理学院 传媒工程学院, 兰州 730000)
文献[1]中用环路增益分析负反馈放大电路的稳定性时,得出逼近自激振荡而不稳定的结论,但没有给出不稳定的范围,不够严谨。本文用幅值和相位裕度的分析方法,在Bode图和Nyquist图中直接得出裕度的范围,用于判断电路的稳定性。然后用文献[2]中的案例进行分析,和文献[1]中的结果进行比较,稳定且自激振荡界限清晰。
1 负反馈放大电路稳定性分析和判断
1.1 稳定性分析

1.2 稳定性裕度定义

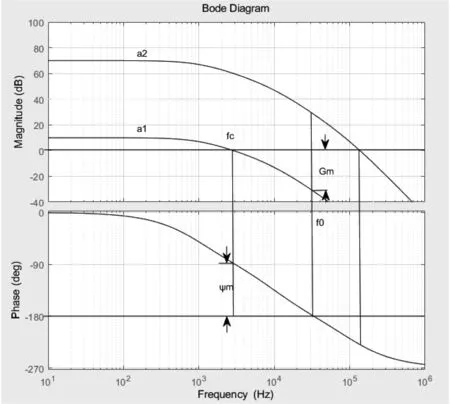
图1 环路增益稳定裕度Bode图
2 案例分析
用稳定裕度判断文献[1]中案例,分别在Bode图中和Nyquist图中设计出稳定裕度范围。
2.1 Bode图分析
在Bode图中判断稳定性如图2所示:
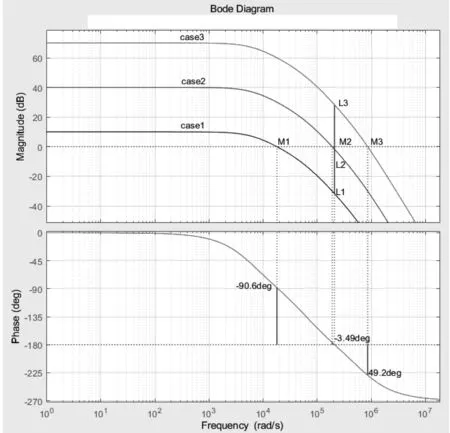
图2 环路增益Bode图
Case1:f=f0时,角频率ω=2.1e+05 rad/s,Gm=-31.7 dB<-10 dB,满足幅值裕度要求;f=fc时角频率ω=1.8e+04 rad/s,φm=91.6°>45°,满足相位裕度要求,电路稳定;
Case2:f=f0时,角频率ω=2.1e+05 rad/s:Gm=-1.7 dB>-10 dB,不满足幅值裕度要求;f=fc时角频率ω=1.9e+05 rad/s,φm=3.49°<45°,不满足裕度要求,但没有达到自激振荡的条件。当频率增大产生更大的附加相移或有外界干扰信号时容易产生自激震荡不稳定;

2.2 Nyquist图中设计稳定裕度
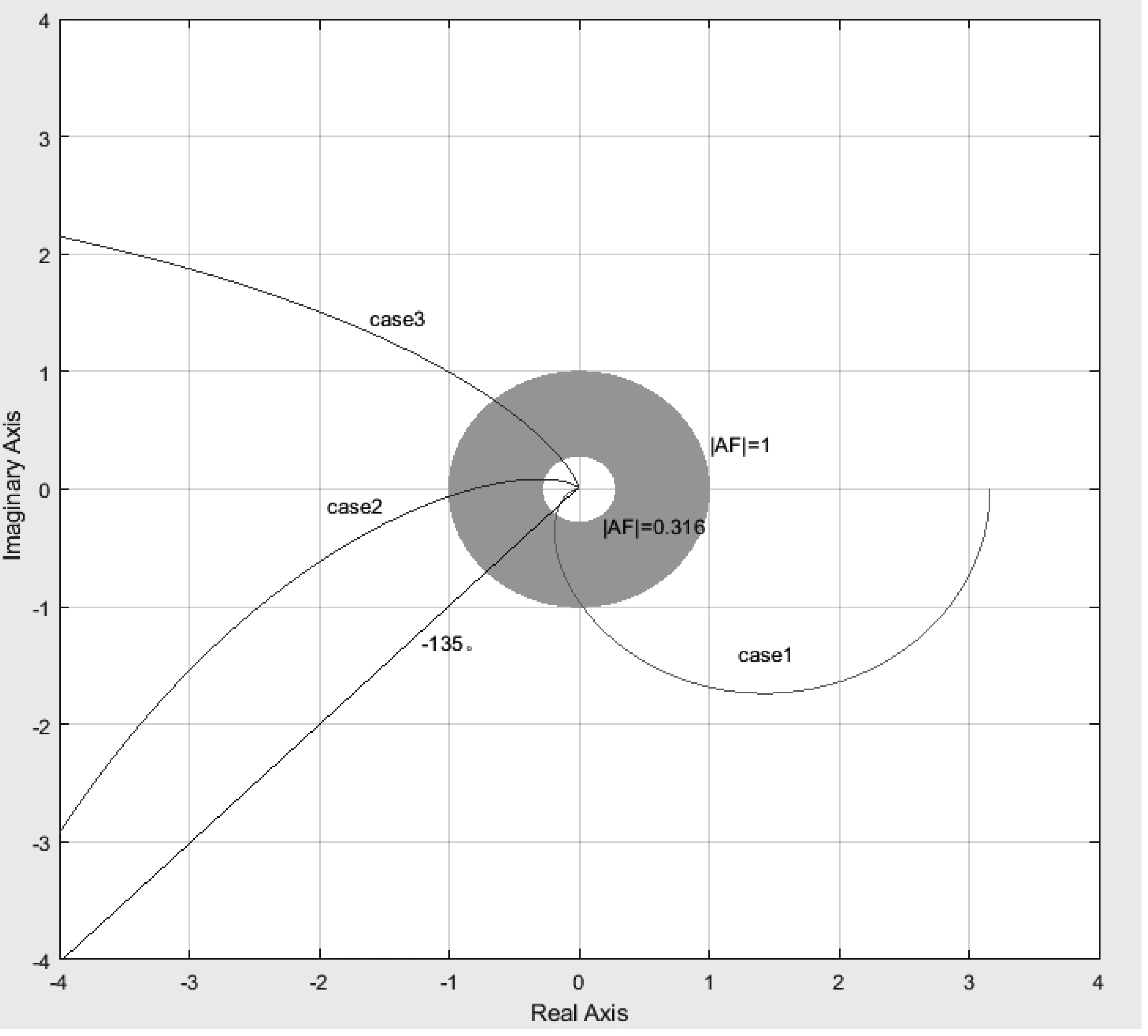
图3 Nyquist稳定性判据
2.3 电路稳定度设计
3 结语
猜你喜欢
心理学报(2022年10期)2022-10-12
装备维修技术(2022年7期)2022-07-01
无线互联科技(2022年4期)2022-05-11
城市道桥与防洪(2022年1期)2022-02-25
河北工业大学学报(2021年4期)2021-09-23
湖北大学学报(自然科学版)(2021年5期)2021-08-20
全球定位系统(2021年3期)2021-08-07
北京航空航天大学学报(2021年6期)2021-07-20
中国新技术新产品(2018年22期)2018-01-05
西江文艺(2017年15期)2017-09-10

