地月平动点轨道应用与研究进展

刘 磊，陈 明，张 哲，刘 勇，马传令

(1.北京航天飞行控制中心，北京 100094；2.探月与航天工程中心，北京 100190)

0 引 言

独特的空间位置和动力学特性使得平动点在空间任务中的应用价值日益凸显，国际上已经在日地L1和L 2点附近实施了多项太阳和宇宙观测任务。1978年第一个日地平动点任务ISEE-3[1]至今，已有12颗探测器进入日地平动点轨道，其中包括我国“嫦娥二号”[2-3]，未来还将实施多项日地平动点任务。

与日地平动点相比，地月平动点同样拥有巨大的潜在应用价值。例如，20世纪60年代提出的利用地月L2点进行月球背面探测[1]、70年代提出的地月L 4和L 5点太空港移民构想[4]、21世纪初提出的利用地月L1和L2点的月球采样探测[5]。NASA于2011年发布了包含平动点的“全局探测路线图”[6]，2012年明确将地月L1和L2点用于未来载人空间任务[7]。不过，与对日地平动点的积极开发和利用相比，目前对地月平动点的实际利用明显滞后，此前国际上仅开展了2项地月平动点验证飞行任务，即美国ARTEMIS任务[8]和我国“嫦娥5T1”地月平动点飞行任务[9-11]。直至2018年5月，我国实施了基于地月L2点中继通信卫星的“嫦娥四号”月球背面探测任务[12]，才标志着人类真正进入对地月平动点的实际开发和有效利用阶段。

对于地月平动点在未来月球和深空探测任务中的实际利用，一方面有数十年的理论和应用研究可供借鉴[13]，另一方面，针对具体应用需求，还存在一些问题有待解决，例如，地月平动点卫星尤其是星座的最优布设、结合任务需求的平动点轨道长期优化维持、平动点卫星的寿命末期处置等。这些问题本质上属于平动点轨道动力学与应用范畴，也是地月平动点未来有效利用的关键所在。文章围绕这些问题调研了国内外研究现状，重点分析了相应发展动态，提出了地月平动点应用构想，梳理总结了相应的关键技术，可为未来地月平动点的研究和利用提供有益思路。

1 国内外研究现状

平动点轨道属于空间多体动力学研究范畴，Farquhar[1]、Szebehely[14]、Howell和Kakoi[24]等对限制性三体问题的研究丰富了平动点轨道动力学理论体系，尤其是为平动点实际应用奠定了坚实的理论基础。下面首先介绍多种地月平动点轨道应用概念及其相关研究，进而重点介绍地月平动点轨道应用中的关键技术—平动点轨道动力学与优化设计和平动点轨道维持控制的研究进展，最后针对未来平动点任务需特别关注的问题—任务末期处置，给出相应的研究现状。

1.1 地月平动点轨道应用研究

国际上地月平动点轨道应用研究主要包括3个方面：月球和深空探测的中继通信、月球和深空探测的低能量转移中枢、地月空间航天器的自主导航支持。

在中继通信应用方面，20世纪60年代Colombo提出了地月平动点中继通信概念，包括基于地月平动点的探月任务交会对接、利用L 4和L 5提供深空中继通信[1]。阿波罗17号任务最初计划利用地月L 2点中继星开展月球背面着陆，后来由于经费削减改为月球正面着陆。面向未来月球采样返回任务需求，Lo等[5]提出利用地月L 2点Halo轨道构成月面Aitken盆地与地面的中继通信链路，如图1所示。对于平动点中继通信的月面覆盖问题，Grebow等[25]的研究结果表明，利用2颗Halo轨道卫星即可实现对月球南极的连续覆盖，3颗则可以提供冗余覆盖。

图1 基于平动点的月球探测与采样返回[5]Fig.1 Lunar exploration and sample return via the libration points[5]

在低能量转移中枢应用方面，21世纪初Lo等[5]率先将动力系统理论引入平动点轨道动力学与轨道设计，提出了IPS理论，设计了利用地月共线平动点的月球取样返回任务，研究结果表明转移飞行所需的能量优于传统的直接转移方法。近几年，NASA积极论证基于地月平动点的载人空间探测任务，提出了用于月球和火星等深空探测任务的地月L 2点空间站概念[26]，包括一个可容纳4人的核心舱。在任务第一阶段，不带航天员的核心舱首先进入L 2点轨道，在轨道上构建完成后，航天员再进入核心舱。在任务第二阶段，使用扩充舱将核心舱质量由28.75吨增加到45.57吨，任务周期由60天延长至500天。

在导航应用方面，20世纪60年代Farquhar[1]率先提出了地月平动点导航概念，包括利用地月L 2、L 4和L 5点为月球和深空探测任务提供导航支持。Carpenter等[27]采用GPS和地月L 2点导航卫星相结合的方式，研究了地月转移轨道段的探测器自主导航问题，研究结果表明导航精度可达1 km和5 cm/s，且地月平动点导航方式更适合于未来月球和深空探测任务。Hill[28]基于平动点轨道的动力学特性，创新性地提出了行星际联合自主导航(LiAISON)。该方法仅利用星间测距或测速方式即可实现平动点导航卫星与用户卫星的联合自主定轨，从而大大增强了航天器的自主导航能力，同时缓解了地面测控网的任务压力。Parker等[29]和Fujimoto等[30]基于LiAISON研究了GEO卫星和地月L1点Halo轨道卫星的自主导航问题，提出了地月平动点星座构想，如图2所示。刘斌等[31]研究了地月三角平动点轨道卫星之间的自主定轨问题。张磊[32]研究了圆型限制性三体问题下的地月平动点导航星座设计问题，分析了地月平动点星座的导航性能。孟云鹤等[33]研究了地月平动点导航星座概要设计，得到了地月L 3点Vertical轨道5星星座。

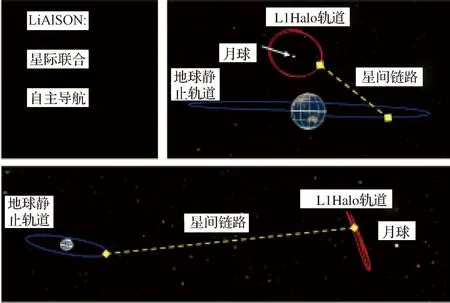
图2 基于LiAISON的GEO与地月L1 Halo轨道自主导航[29]Fig.2 Autonomous navigation of GEO and the Earth-Moon L1 Halo orbit based on LiAISON[29]

在实际任务方面，美国ARTEMIS任务实现了国际首次地月平动点验证飞行。2010年，美国将两颗任务末期的THEMIS探测器转移进入地月L1和L2点附近轨道，并在约11个月后进入环月轨道[8]，即ARTEMIS任务，如图3所示。

图3 ARTEMIS任务[8]Fig.3 The ARTEMIS mission[8]

2014年11月1日，我国成功完成“嫦娥5T1”月球再入返回试验任务，为了实现对任务资源的最大利用，决定利用探测器的服务舱开展地月L 2点飞行任务。在4次地月转移轨道控制后，“嫦娥5T1”服务舱于11月23日15时左右到达近月点，经过近月制动后，飞向地月L 2点并进入Lissajous轨道。“嫦娥5T1”服务舱在L 2点Lissajous轨道飞行期间，基于我国测控条件，共实施了2次平动点轨道维持控制[34]，最终在约1.5个月后返回月球，进入高度200 km、倾角45°的环月圆轨道，飞行过程如图4所示[10-11]。

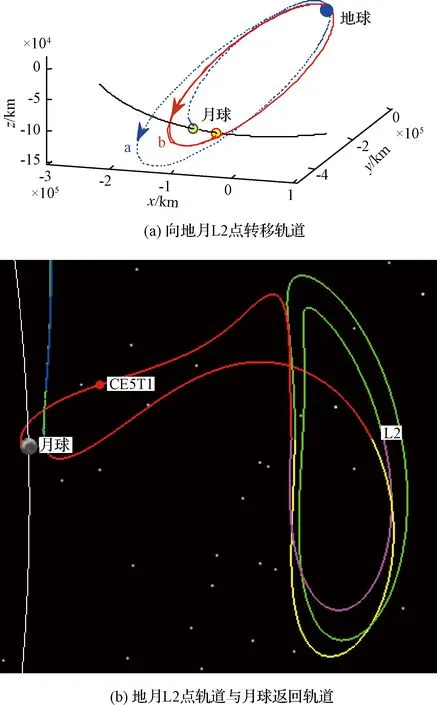
图4 “嫦娥5T1”地月平动点飞行[10-11]Fig.4 Flight of the Earth-Moon libration point of CHANG’E-5T1[10-11]

“嫦娥5T1”服务舱实现了国际首次利用月球近旁飞越方式进入地月平动点轨道，我国由此成为继美国之后唯一开展地月平动点飞行的国家。该任务的成功直接促成了我国“嫦娥四号”月球背面探测任务，也为未来利用地月平动点的空间任务提供了有益借鉴。

2018年5月，我国开始实施“嫦娥四号”任务，主要任务目标为月球背面着陆与巡视探测。为了保障探测器在月面着陆后与地面测控网的通信，特地在地月L2点Halo轨道布设了中继卫星“鹊桥”[12]，其发射和转移布设轨道如图5所示。

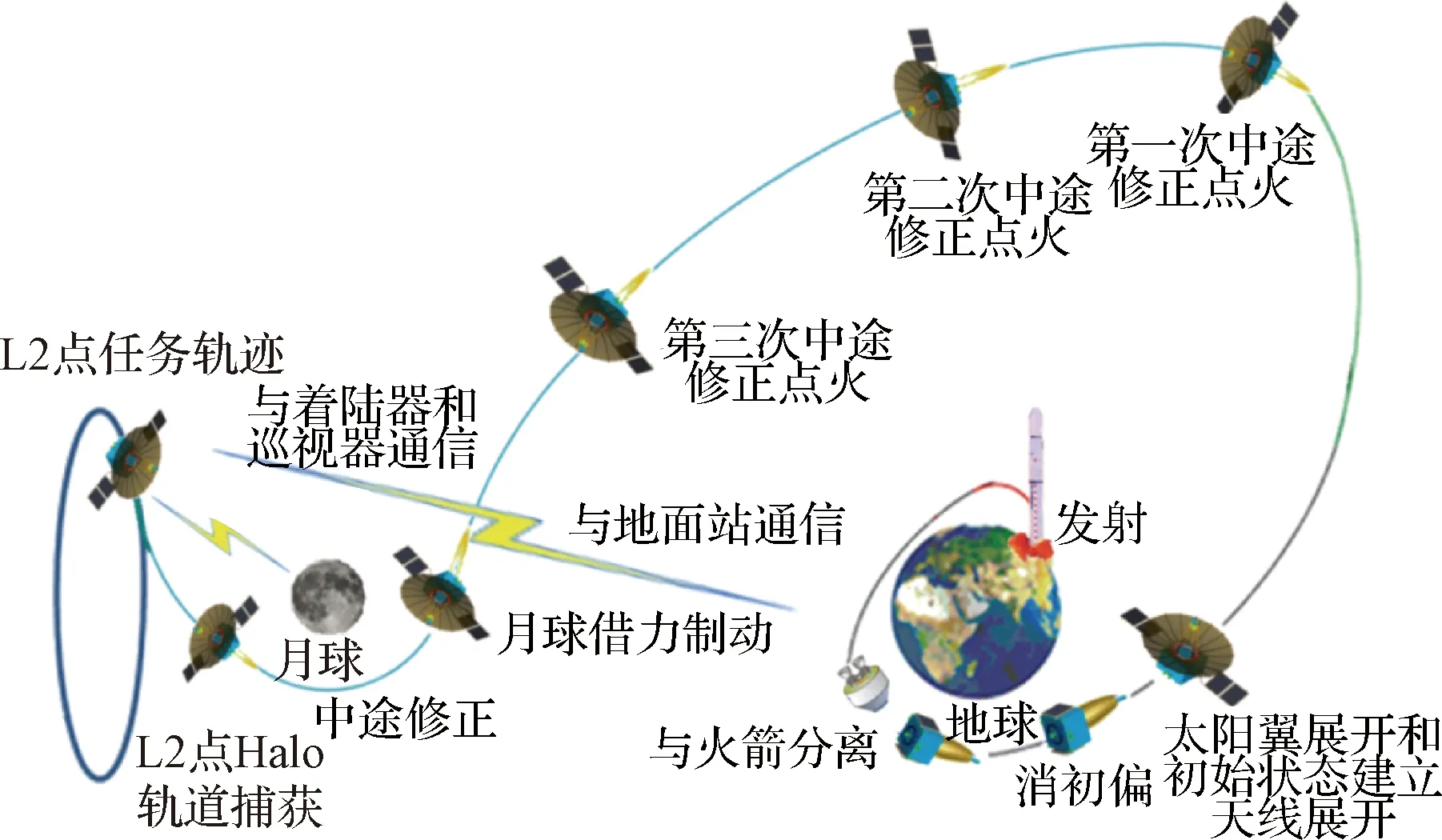
图5 “嫦娥四号”地月平动点中继星飞行轨道[12]Fig.5 Flight trajectories of relay satellite of CHANG’E- 4[12]

2019年1月3日，“嫦娥四号”着陆器利用“鹊桥”提供的中继通信链路，成功软着陆于月球背面，由此实现了国际首次月球背面软着陆，同时拉开了对地月平动点有效实际利用的序幕。

1.2 轨道动力学与优化设计

近年来围绕月球、平动点和地外天体探测等深空任务的轨道应用需求，众多学者开展了椭圆型限制性三体问题(ER3BP)、包含摄动力的多体动力学、空间多体轨道优化设计等研究，希望借助多体动力学达到节省探测能量和利用混沌运动特性的目的。

Belbruno等[35]在1987年用数值方法发现了借助太阳引力的地月低能转移轨道，提出了月球弹道捕获概念并发展为弱稳定边界(WSB)理论，基于该理论在1991年为失败的Hiten任务设计了低能量奔月轨道，还为SMART-1任务设计了地月低能量转移轨道。文献[36-38]提出了IPS理论，开发了平动点任务设计软件LTool，研究了Genesis任务轨道设计与控制、月球低能量转移轨道、木星与彗星的共振和捕获轨道、木星卫星间的低能量转移轨道等，此外利用IPS理论为NASA的Origin项目提供轨道支持，包括Genesis、MAP、SIRTF、SIMS、StarLight、NGST、TPF等任务。西班牙Gómez等[39-40]在平动点轨道动力学与轨道设计方面也做了大量研究。

近几年，在地月平动点中继通信和自主导航等应用需求的牵引下，出现了一些地月平动点轨道设计的新方法，而且地月L 3～L 5点动力学和轨道设计也逐渐受到关注。Dunham等[41]研究了从地球停泊轨道到地月L 2点的直接转移轨道和间接转移轨道，以及从L2点返回地球的任务轨道，总飞行时间17天，转移控制所需速度增量为386 m/s。Haapala等[42]研究了地月空间任务轨道交互设计软件，用户可以借助图形界面选择满足任务需求的多体轨道段，进行L 3～L 5点转移轨道的拼接设计，如图6所示。Davis等[43]基于动力系统理论研究了从地球到地月L 3点Halo轨道的转移轨道，提出了“伪流形”概念，如图7所示。文献[44-45]研究了地月L 1/L 2点转移轨道的初步设计和保持问题，给出了地月平动点轨道分类，以及不同类型轨道间的关系和各自动力学特性，用于辅助地月空间快速轨道设计，如图8所示。

图6 地月空间任务轨道交互设计软件界面[42]Fig.6 Interface of interactive design software of trajectories in the cislunar space[42]

Abraham等[46]研究了从LEO到地月平动点的双脉冲转移轨道，结合粒子群优化和打靶法进行轨道设计。Peng等[47]借助三维流形，研究了向地月多圈椭圆Halo轨道的直接转移轨道。刘磊等[9]研究了“嫦娥5T1”拓展任务轨道设计[10-11]和基于平动点的月球探测器应急轨道设计[48]，给出了平动点间的转移轨道方案和平动点轨道的直接转移入轨方法。安然等[49]采用Lyapunov最优反馈控制方法和遗传算法，计算得到了时间最优的地月L 2点Halo中继星小推力转移轨道。潘迅等[50]在限制性三体问题下，给出了一种平动点双脉冲转移的高效计算方法。张景瑞等[51]研究了月球借力条件下，向地月L 2点Halo轨道的低能量转移问题，梁伟光等[52]研究了解析计算方法在地月L 2点Halo轨道设计中的应用。

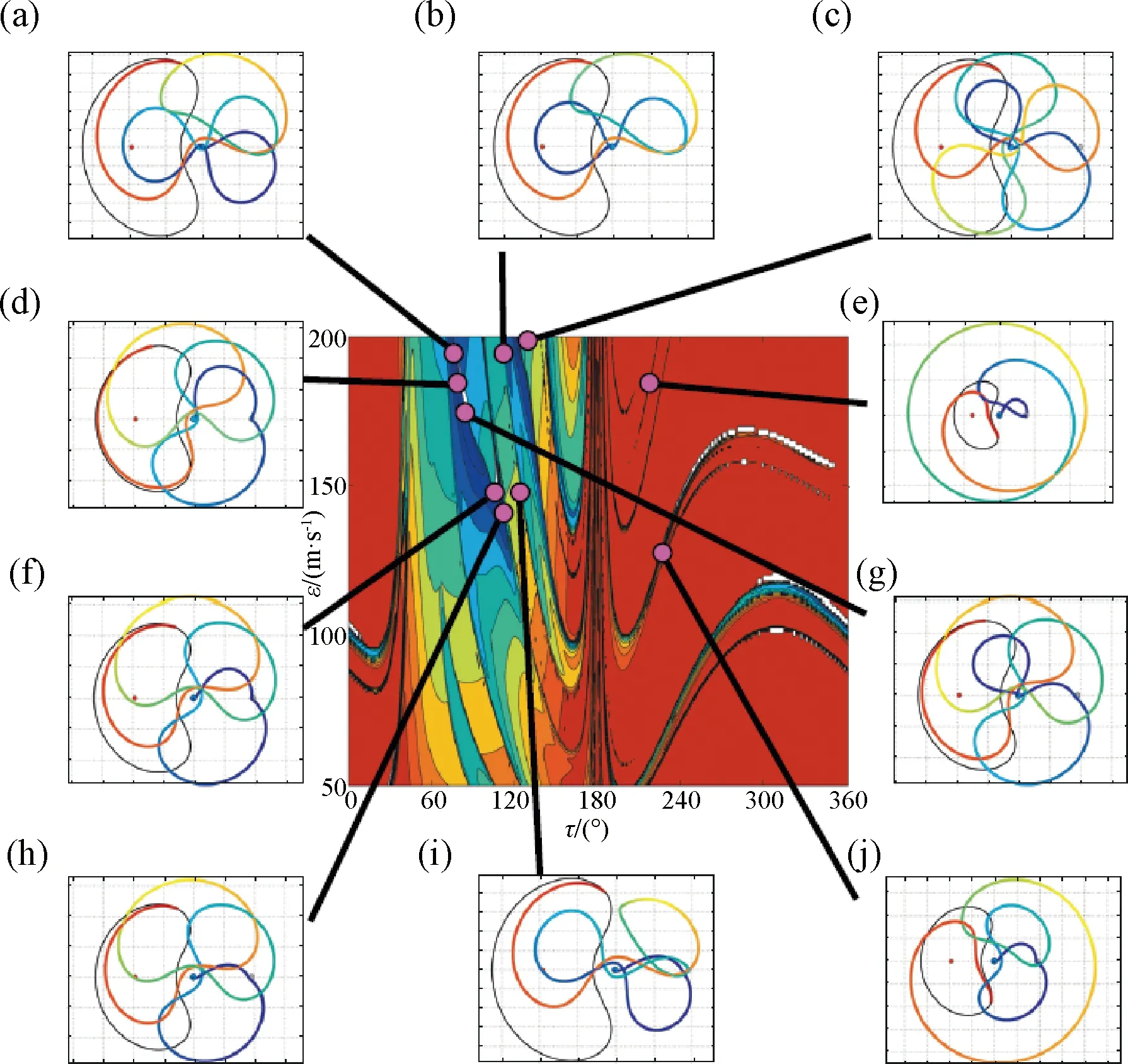
图7 地球至地月L 3点转移轨道设计[43]Fig.7 Trajectory design of transfer from the Earth to the Earth-Moon L 3 point[43]

在实际任务方面，ARTEMIS任务P1探测器由2010年2月开始转移，至9月进入地月L 2点拟Halo轨道，P2探测器于10月经由地月L 2点进入地月L 1点拟Halo轨道。ARTEMIS转移飞行时间较长的主要原因是借助了多次月球引力辅助和深空机动。相比较而言，我国“嫦娥5T1”服务舱向地月平动点轨道的转移飞行时间较短。在2014年11月1日再入返回试验结束后，服务舱经过约1.5圈地心大椭圆轨道到达月球附近，借助近月制动进入地月L 2点轨道，整个转移飞行时间约27天[10-11]。“鹊桥”中继星于2018年5月21日发射至6月14日进入地月L 2点Halo轨道，转移时间约24天。

图8 地月空间轨道设计[44]Fig.8 Trajectory design in the cislunar space[44]

1.3 平动点轨道维持控制

受动力学不稳定性、天体摄动、光压摄动、入轨偏差、动力学模型误差等诸多因素影响，平动点轨道的稳定性和维持控制问题一直备受关注。

20世纪80年代初，国际上提出了Halo轨道维持问题，相应控制策略主要有Target模式和Floquet模式。前者由Farquhar和Breakwell提出[1]，以跟踪标称轨道为控制目标，通过控制将探测器导引到期望位置，该方法具有控制系统的一般结构，设计思路较为简单，易于工程实现。后者由Gómez等提出，主要基于Halo轨道的不变流形结构，通过抑制不稳定流形的发散趋势进行轨道维持，该方法控制消耗较少但具有一定理论难度。此外，Howell等基于线性控制思想，研究了Halo轨道的渐近跟踪。Wong等[53]基于自适应学习控制理论，设计了控制器和滤波器并给出了稳定性证明。Rahmani等[54]和Kulkarni等[55]分别利用最优控制理论、序列二次规划、H∞理论等实现了Halo轨道的渐近稳定控制，Kulkarni等[55]将研究结论进一步推广到Halo编队飞行控制。Ming等[56]基于最优控制理论提出了L2点轨道的闭环次优反馈控制。

近几年，平动点轨道维持研究倾向于高精度力模型和任务轨道以及采用现代控制理论和方法。例如，Roberts等[57]研究了DSCOV任务避免日凌的维持问题，提出了频率为3个月和6个月的控制策略，结果表明用于避免日凌的控制消耗比站位保持消耗大2个量级，如图9所示。Zhu等[58]提出了一种干扰消除的站位保持方法，该方法使用误差驱动而非基于模型的控制律，因此不受模型精度和线性化的影响。Nazari等[59]针对地月Halo轨道维持问题，研究了基于连续LQR控制、Floquet理论和周期控制增益的站位维持策略，仿真结果表明所述方法优于传统反馈线性控制器。Pavlak等[60]研究了一种地月平动点轨道长期站位保持策略，该策略无需严格维持在标称轨道并考虑了后续离轨控制。文献[8,61-62]面向ARTEMIS轨道维持需求，提出了最优连续轨道控制策略，并与动力系统理论中的稳定模态分析进行了对比，数值仿真结果表明该方法所需速度增量较小，如表1所示。朱敏[63]研究了太阳帆人工平动点轨道动力学，提出了太阳帆人工平动点轨道自抗扰保持控制器。文献[64-65]研究了太阳帆人工平动点轨道维持与优化问题，利用了哈密顿保结构控制器。刘刚等[66]研究了圆型限制性三体问题下的绳系卫星Halo轨道控制问题，设计了基于非线性模型预测控制的控制器。文献[67-69]研究了我国日地L 2点轨道和地月L 2点轨道的维持方法和策略。

图9 DSCOV任务轨道维持分析[57]Fig.9 Analysis of orbit maintenance for DSCOV[57]

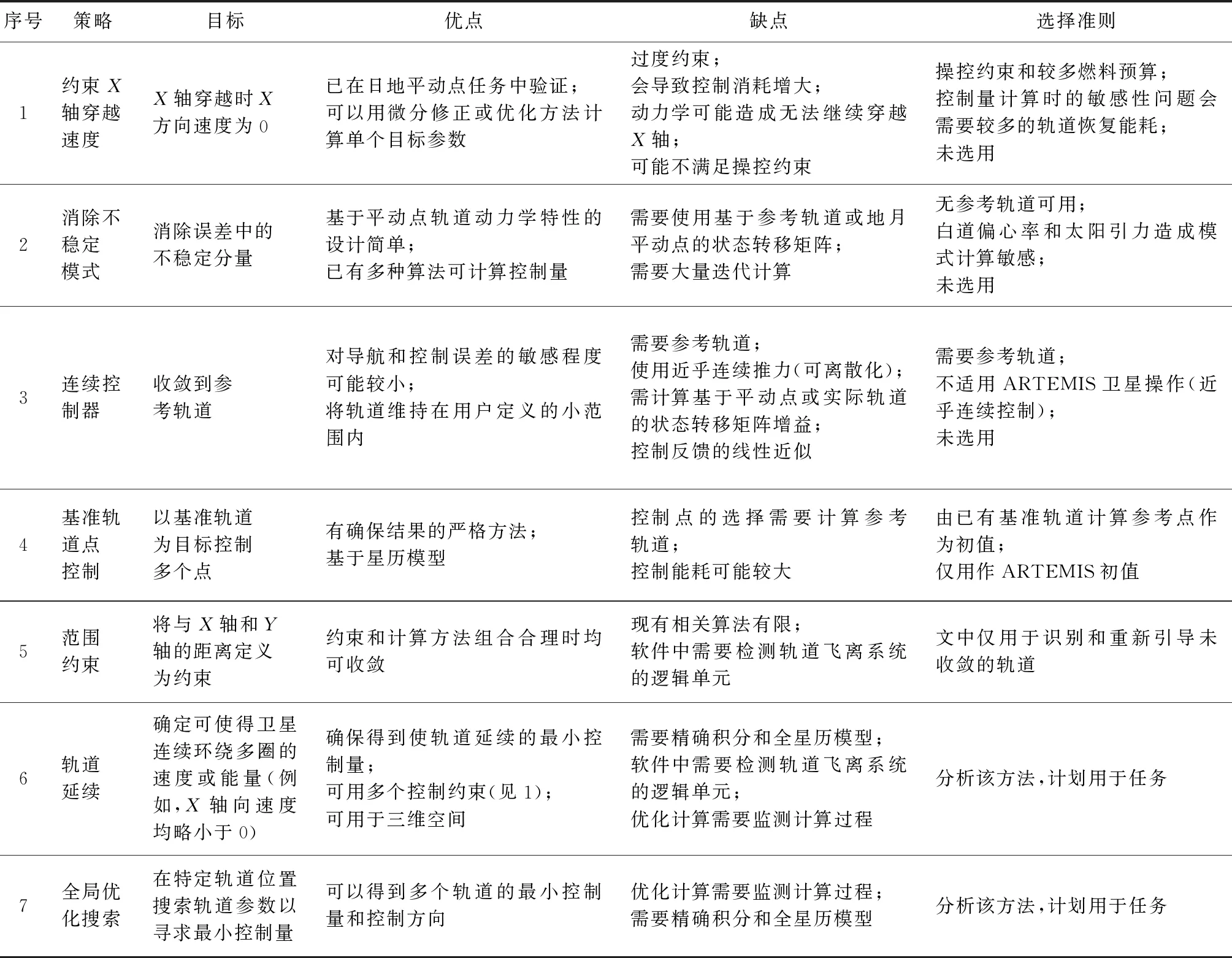
表1 ARTEMIS控制策略选择准则[62]Table 1 Control strategies and selection criteria examined for application to ARTEMIS[62]

在实际任务方面，ARTEMIS任务在地月会合坐标系X轴附近施加控制，控制探测器可以连续环绕平动点轨道1.5圈，控制速度增量优于每年10 m/s[61]。“嫦娥5T1”服务舱和“鹊桥”中继星在地月L 2点飞行期间的轨道维持，采用了类似的平动点连续环绕控制策略[34]，从目前维持效果看，“鹊桥”中继星每年维持速度增量可以优于10 m/s。

1.4 平动点任务末期处置

近30年来，随着平动点任务日趋增多，平动点探测器的任务末期处置问题日益凸显。受动力学特性影响，平动点探测器在无控条件下不会长期稳定在平动点附近，优点是不会给平动点区域造成空间垃圾，缺点是混沌运动特性可能造成探测器接近地球，从而严重威胁地球卫星安全，甚至再入地球大气层和陨落在城市等人口稠密地区，造成重大事故。例如，目前日地平动点探测器Herschel重达2.8吨[25]，前述NASA规划的地月L2点空间站更是重达45.57吨，如此重量的航天器若无控到达地球附近并再入大气层，其毁灭作用难以估量。

近几年，国外开始关注日地平动点任务末期处置问题。2013年，欧空局提出了日地平动点轨道和大椭圆地心轨道的寿命末期处置问题，考虑利用多种手段进行处置，包括多体动力学、太阳光压、地球重力场和大气阻力等。文献[70-71]以日地平动点探测器Herschel、SOHO和Gaia以及两个大偏心率地心轨道任务INTEGRAL和XMM为研究对象，研究了这些探测器寿命末期的处置方案及其动力学模型和设计方法。Alessi等[72]研究了Gaia探测器寿命末期再入地球的处置方案，如图10所示。Soldini等[73]研究了利用太阳光压的平动点探测器寿命末期处置方案，讨论了寿命末期处置准则。Armellin等[74]以SOHO和Gaia探测器为研究对象，研究了如下寿命末期处置方案：撞击月球、返回再入地球和日心坟墓轨道，如图11所示。Olikara等[75]研究了日地L1/L2点探测器的任务末期处置问题，考虑借助不稳定流形和轨道机动阻止探测器返回地球，分析了大幅值日地L2点Lissajous轨道上的探测器的处置控制能耗，如图12所示。

图10 Gaia返回地球方案[72]Fig.10 Scheme of Earth reentry for Gaia[72]

图11 SoHO返回并撞击月球方案[74]Fig.11 Scheme of SoHO transfer to and impact on Moon[74]

在实际任务的末期处置方面，以往平动点任务在设计之初往往不考虑该问题，而是在任务结束时设计拓展任务，以求最大程度利用探测器价值，或者将探测器直接送入坟墓轨道。ISEE-3任务结束后，首先受控进入日心轨道开展彗星探测，其后于2014年8月再次接近地球[1]。NASA的WMAP探测器在日地L 2点任务结束后，经多次任务规划于2010年10月离开L 2点进入日心轨道。Genesis探测器在完成日地L 1点任务后，于2004年9月8日再入地球并返回采样，之后探测器平台再次飞往日地L 1点附近，并于2005年2月1日离开L 1点，最后进入日心轨道。ESA的Herschel探测器在平动点任务结束后，于2013年5月机动变轨进入日心轨道，按照轨道设计结果至少300年不会返回地球附近，同年10月Planck探测器也在任务结束后被送入日心轨道[75]。“嫦娥二号”在日地L2点任务完成后，于2012年4月15日飞离L2点开展4179小行星探测任务，12月13日成功获取了4179小行星的近距离光学图像，最后进入日心轨道[76]。至于地月平动点任务，ARTEMIS探测器和“嫦娥5T1”服务舱在完成地月平动点验证飞行后，均飞向月球成为环月卫星。

图12 幅值60万km的日地L 2点Lissajous轨道探测器的处置控制消耗[75]Fig.12 Maneuver costs along unstable manifold for 600,000 km L 2 Lissajous orbit[75]

2 发展动态分析

分析以上国内外研究现状和发展动态，可以得到如下结论：

1)在地月平动点轨道应用研究方面，国外从20世纪60年代开始就提出了中继通信和导航以及地月平动点空间站等应用概念，开展了大量相关理论和技术研究，率先实现了地月平动点验证飞行。国内近10年来进行了积极跟踪研究，尤其是在国际上首次实现了对地月平动点的实际有效利用，不过，在自主创新性概念和突破性理论成果方面还有待加强。

2)在地月平动点轨道动力学与轨道设计方面，目前研究多集中于L 1和L 2点，研究重点较为单一地考虑能量因素，近年来L 3～L 5点轨道动力学尤其是转移轨道优化设计，逐渐受到国内外关注。

3)在地月平动点轨道维持方面，目前维持策略仍以Target和Floquet模式为主，虽然已经出现了部分基于最优控制理论的相关研究，但是目前尚未应用于实际任务，后续需充分结合实际任务约束开展进一步研究。

4)在地月平动点任务末期处置方面，国外在近几年开始着手研究日地平动点任务的末期处置问题，考虑到地月平动点更为复杂的动力学特性，尤其是地月平动点探测器到达地球的时间更短，对地球造成的威胁更大，因此亟需加强相关研究。

3 未来应用构想

目前我国航天活动范围正快速向深空发展，已经实现了月球背面着陆和巡视探测，2019年底和2020年还将计划实施月球采样返回任务和自主火星探测任务，月球基地建设、载人登月探测和小行星探测等深空探测任务正在积极规划论证和组织实施。对于我国未来这些月球和深空探测任务，地月平动点具有深远应用潜力，可望发挥巨大应用价值。

例如，可以考虑利用多个地月平动点卫星组网形成导航星座，或与地面测控网联合组成天地基测控系统，直接为月球探测器提供相应的中继通信、月面定位和各飞行阶段的自主导航等支持，甚至为整个地月空间甚至月球以远的探测器提供中继通信和导航定位服务，从而在弥补地面测控不足、减轻地面测控压力和提高探测器导航定位精度与自主能力等方面，最大程度地发挥地月平动点的重要作用。图13以地月L1和L2点卫星组网为例，给出了地月平动点导航星座应用构想。

图13 地月平动点导航星座应用构想Fig.13 Concept of constellation of Earth-Moon libration points

此外，地月平动点可作为未来地外天体探测任务的转移中枢和开发利用场所。国际上Lo等[36]已经提出了利用不同平动点轨道的不变流形，相互拼接构成深空探测低能量转移通道，从而实现太阳系乃至更广范围的空间探测。在此基础上，可以考虑利用地月平动点作为未来地外天体探测的低能量转移中枢，探测器由地月平动点出发前往小行星等地外天体，实现伴随、环绕和着陆等多种形式探测。更进一步，可以考虑将探测器附着于小行星表面，而后施加推力将小行星转移至地月平动点附近实现捕获，使之长期稳定驻留在地月空间，为后续科学研究、采集高价值矿产等开发利用提供先决条件。图14给出了地月平动点的小行星探测应用构想，其中小行星捕获后的目的地包括动力学特性稳定的地月三角平动点。

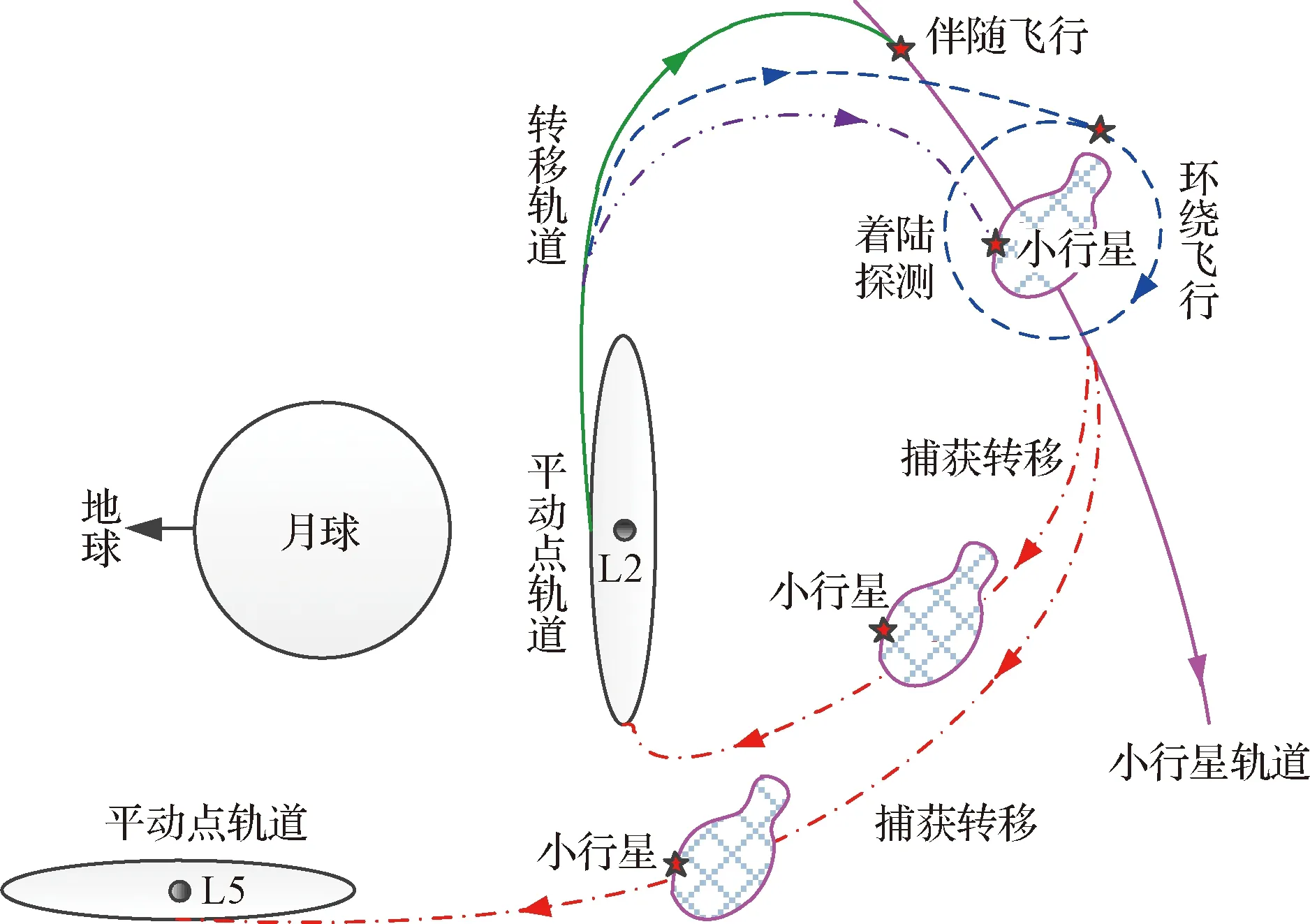
图14 地月平动点的小行星探测应用构想Fig.14 Concept of asteroid exploration using Earth-Moon libration points

为了最终实现上述应用构想，需要基于平动点已有研究基础，结合未来实际应用的需求，针对其中的关键技术问题，开展平动点轨道动力学与应用研究，例如地月平动点星座的优化布设、结合性能需求的星座长期维持、星座任务末期处置、地月平动点轨道优化设计与控制等，最终实现地月平动点应用的低成本、高价值、高性能和高安全性。

4 结 论

我国空间活动范围正由近地向深空快速延拓，在未来相当长时间内，月球和深空探测将是我国和国际空间活动的重要内容。不难预见，未来空间探测活动对低能量转移、中继通信、导航定位等技术的需求会日渐凸显，而平动点则有望成为未来满足这些重要技术需求的新手段。与此同时，虽然目前平动点轨道动力学理论研究较为充分，但是面向未来可能出现的地月平动点大规模实际开发和充分利用，如地月平动点导航星座的构建与应用、基于地月平动点的载人深空探测和地外天体探测与利用等，仍需围绕地月平动点轨道理论与应用开展诸多针对性研究。