系统参数对电动力绳系动力学的影响
杨育伟,蔡 洪
(国防科技大学空天科学学院,长沙 410073)
0 引 言
电动力绳系是一种由两个卫星和一条柔性可导电的系绳组成的空间飞行器系统。其中,卫星连接于系绳的两端[1]。在与地磁场及电离层的作用下,电动力绳系能够感应产生洛伦兹力,从而用于轨道机动[2]。由于具有不消耗燃料、质量轻及功率大等优点,电动力绳系技术在空间碎片清除和废弃卫星降轨等空间任务中具有非常广阔的应用前景[3-8]。而在当前的理论研究中,电动力绳系的摆动动力学和轨道动力学研究是重点关注的问题。
在对电动力绳系的摆动动力学的研究中,周期摆动是关注最多的问题[9-14]。Peláez等[11- 12]首先提出了哑铃模型且推导了在圆轨道和椭圆轨道上运行的电动力绳系的摆动动力学方程。该方程具有非常强的非线性,在一定的参数范围内存在周期解。通过Poincaré映射法[11]和Legendre伪谱法[13]等数值方法可以求解得到方程的周期解。由于电动力绳系是处于电动力的周期激励下,周期摆动从本质上是不稳定的。通过计算周期解迁移矩阵的特征值,Peláez和Andrés[12]发现不稳定性随着电动力参数和轨道偏心率的增长而增长。
降轨动力学是研究电动力绳系轨道动力学的重要问题之一[15-19]。胡长伟等[15]研究了系统与空间等离子体之间的接触电阻对离轨特性的影响。张健等[16]通过系绳结构的设计,实现了系绳稳定与轨道机动控制的解耦,并研究了气动阻力作用下系统的动力学及控制特性。文献[17]中运用高斯扰动方程对绳系-纳星的轨道动力学进行了建模。文献[18-19]对保证快速、稳定的飞行器降轨的电流控制进行了研究,通过比较不同轨道倾角下的降轨时间得出:电动力绳系的降轨效率与轨道倾角和系绳摆动相关。
在摆动动力学和轨道动力学方程中,存在系统参数:主星质量、子星质量、系绳质量和系绳中电流。在所有对电动力绳系动力学的研究中,上述系统参数对系统摆动动力学和轨道动力学的影响的研究较少。Wang等[20]研究了系统总质量与主星质量的比和子星质量与总质量的比对降轨稳定性和效果的影响。然而,每个系统参数对轨道动力学的影响并没有研究。因此,本文将研究:1)系统参数对摆动动力学的影响;2)系统参数对轨道动力学的影响。
1 系统参数对摆动动力学的影响
1.1 坐标系统
下面介绍文中用到的两个坐标系。
1)地心惯性坐标系EXYZ:该坐标系以地心E为原点,EX轴指向第一升交点,EZ与地球自转轴重合,EY符合右手定则。
2)轨道坐标系Oxyz:该坐标系以电动力绳系的质心O为原点,Ox轴沿当地垂线并指向天顶,Oz轴沿轨道动量矩的方向,Oy轴符合右手定则。
1.2 摆动动力学方程和周期解
文中仅研究在留位状态阶段系统参数对电动力绳系摆动动力学的影响。本阶段中,系统的系绳处于张紧状态,绳长保持不变。因此,将电动力绳系假设为哑铃模型,该模型将系绳视为非弹性且无柔性的细杆[11-12]。虽然在空间运行的电动力绳系的系绳长度可达几千米,但与轨道半径相比仍然是小量。因此,在建模过程中,假定沿系绳周围空间的地磁场是均匀的,且取系统质心处的值。为了计算作用于系绳上的电动力,需要对地磁场B建模。本文使用了最简单的地磁场模型—非倾斜偶极子模型。在轨道坐标系Oxyz中,该模型的各分量(Bx,By,Bz)可表示为
(1)
式中:r为轨道半径,μm为磁偶极子强度,i为轨道倾角,为近心点角距,f为真近点角。
定义系绳在轨道坐标系的平面Oxy内的投影与Ox轴的夹角为面内角θ,系绳与平面Oxy的夹角为面外角φ,用θ和φ来描述电动力绳系的摆动动力学。对于电动力绳系,主星及子星的尺寸与绳系的长度相比很小;另外,主星与绳系之间、子星与绳系之间的连接均为柔性连接。基于这两个因素,系统的主星与子星的姿态对系统摆动的影响在本文中忽略不计。空间中电动力绳系模型和各坐标系如图1所示。
基于哑铃模型和非倾斜偶极子磁场模型的假设,运行于椭圆轨道上的电动力绳系的摆动动力学方程可表示为[14]

图1 电动绳系哑铃模型和坐标系示意图Fig.1 Dumbbell model of EDT and coordinate systems
(2)
其中,e为轨道偏心率。在式(2)的推导过程中,将变量对时间的求导变换为了对真近点角f的求导,即式中求导符号(·)表示d( )/df。另外,在推导中,引入了电动力参数ε,其表达式为
(3)
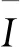
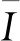
在电动力绳系的运行过程中,虽然在洛伦兹力作用下,系统会产生轨道机动,但是与系统的摆动相比,轨道元素如偏心率、轨道倾角及近地点高度的变化非常缓慢。因此,本文中在研究摆动动力学时,假设系统的轨道保持不变。此时,式(2)中包含参数ε的激励项具有周期性,在一定的参数范围内,其具有周期解。但由于式(2)具有很强的非线性,只能采用数值方法来对其进行研究。
采用数值方法进行研究时,需令
(4)
将摆动动力学方程(2)表示为一阶形式。

图2 不同ε值对应的周期解Fig.2 Periodic solution of libration dynamic equation for different ε
摆动动力学方程的周期解,可以通过Poincaré映射等数值方法求解得到[11]。摆动动力学方程的周期解对电动力绳系具有非常重要的意义,其表示系统能量输入为零的状态,且可以作为空间操作的参考轨道。因此,本文研究系统参数对摆动动力学方程的周期解及其特性的影响。
在摆动动力学方程中,各系统参数通过ε来影响该方程。图2为当i=40°,e=0.2,=0°时,不同ε值对应的周期解。为了不失一般性,算例中i和e的值是随机选取的,并没有特殊含义。
图2显示,对于不同的轨道参数,随着ε的增长,摆动动力学方程周期解的摆动幅度也在增大。电动力绳系摆动动力学方程的周期解是不稳定的[12]。周期解的不稳定性越强,在无控制状态下,当系统受到扰动时,周期摆动状态会越快地发生偏离,变为转动运动。而将非周期摆动控制为周期摆动时,此时各参数对应的周期解不稳定性越强,控制越难实现。非线性动力学方程周期解的不稳定性可以通过周期解的迁移矩阵的特征值的模来表征。
1.3 稳定性分析理论
令
(5)
为基于参量σ的n维自治系统的非线性微分方程。当σ=σ0时,如果系统(5)存在周期解,则周期解的局部稳定性由该系统的线性化方程决定,即

(6)
式中:A(t)=∂f(x,σ)/∂x|x=x0(t),σ=σ0为雅阁比矩阵。由于x=x0(t)具有周期性,A(t)为周期时变矩阵。
此时,将非线性系统(5)的周期解稳定性判断近似转化为线性系统(6)的周期解局部稳定性判断问题。而线性系统周期解的稳定性可通过Floquet理论来判断[21-22]。设n×n的非奇异矩阵Φ(t)为系统(6)的基解矩阵(Fundamental matrix),即
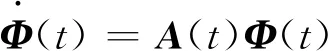
(7)
另外,存在周期为T的n×n非奇异矩阵P(t)和n×n常值矩阵R满足
Φ(t)=P(t)etR
(8)
而迁移矩阵(Monodromy matrix)Φ(T)为当t=T、初值条件Φ(0)=I(I为单位阵)时Φ(t)的值;Φ(T)的特征值称为Floquet特征乘子。
参考文献[21-22]中有以下结论:方程(6)的周期解渐近稳定的必要条件是方程(6)的特征乘子的模都小于1(所有的特征乘子在复平面的单位圆内)。否则,周期解是不稳定的。另外,模大于单位1的特征乘子的模越大,周期解的不稳定性越强。
对于摆动动力学方程,周期解的迁移矩阵有两对特征值。其中至少有一个特征值的模大于单位1[12]。本文用迁移矩阵特征值的模即周期解的不稳定性来衡量系统参数对电动力绳系摆动动力学的影响。在仿真中采用了文献[23]介绍的基于精细积分的迁移矩阵计算方法。
1.4 系统参数对摆动动力学的影响仿真
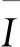
仿真中,分别计算了不同系统参数对应的周期解以及周期解迁移矩阵特征值的模随系统参数的变化关系。图3给出了周期解迁移矩阵的特征值的模随各系统参数的变化关系。针对每个系统参数的仿真中,该系统参数的变化范围如图3中对应各子图中的横坐标所示,而其余参数的值保持恒定,且取表1中的值。本文假设系绳的长度与质量呈正比,因此图3(c)中存在两个横坐标:系绳质量mt,以及对应的绳长L。另外,在所有的仿真中,轨道元素设为e=0.1,i=25°,=0°。

表1 参考系统的系统参数的值Table 1 Values of system parameters of the baseline system
由图3可知,对于所有的系统参数,均存在模大于单位1的特征值λ3,4,说明对应的周期解均是不稳定的。
2 系统参数对轨道动力学的影响
2.1 轨道动力学方程
为了避免当轨道偏心率或者轨道倾角非常小时造成的奇异性,航天器的轨道运动可以用春分点轨道元素的形式来描述。春分点轨道元素和经典轨道元素之间的关系可表示为
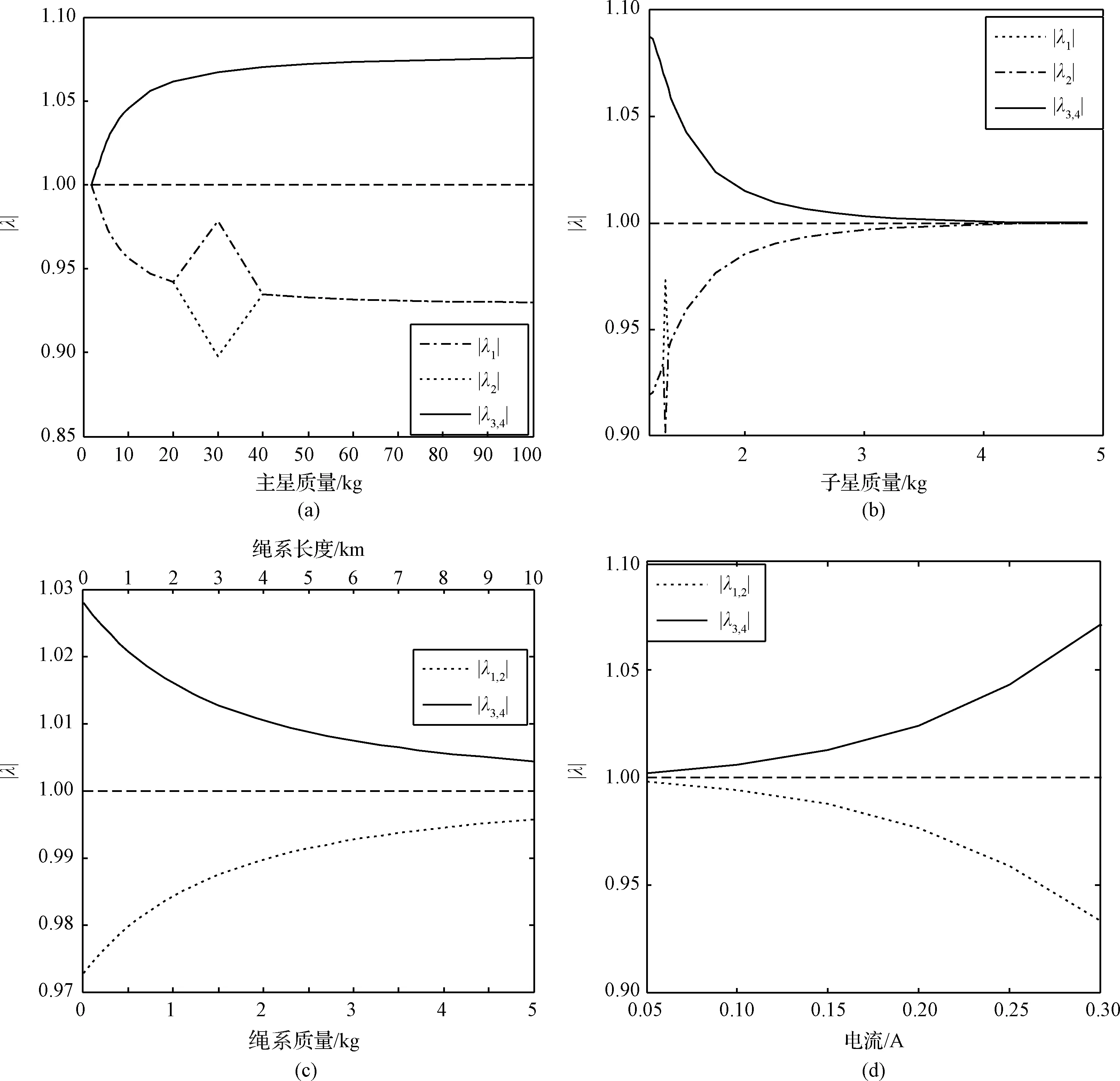
图3 周期解迁移矩阵特征值的模与系统参数的关系Fig.3 Moduli of eigenvalues of monodromy matrix as functions of system parameters

(9)
其中,a为轨道长半轴,Ω为轨道升交点赤经,λ为平经度,M为平近点角;h,k,p和q分别为用来代替经典轨道元素e,i,Ω和的对应变量。则以春分点轨道元素描述的系统轨道动力学方程为
(10)
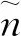

(11)
作用在系绳上的洛伦兹力FL可以表示为
(12)
其中,t为与系绳相切的单位向量,它在轨道坐标系中的表达式为
t=cosθcosφi+sinθcosφj+sinφk
(13)
本文仅考虑洛伦兹力和重力作用于系统上,则由洛伦兹力引起的扰动加速度(S,T,W)为
(14)
将式(1)、(14)和(13)代入式(15),可得
(15)
在洛伦兹力的作用下,电动力绳系可进行降轨。本文通过系统参数对降轨过程的影响来研究系统参数对轨道动力学的影响。在降轨时,轨道长半轴的变化率可表征电动力绳系的效率。在式(10)中,da/dt依赖于加速度分量S和T。令Ta表示项(1+ecosf)T在一个轨道周期内的平均值。在一个轨道周期内,项esinfS的积分远小于Ta的积分。因此,分量T为决定轨道长半轴变化率的最主要因素。
令
(16)

式(15)中计算T时,地磁场分量Bx所占的比重远大于分量Bz。则T主要依赖于项-Bzcosθcosφ和ζ。从而,da/dt主要由-Bzcosθcosφ和ζ决定。本文降轨过程中系绳的摆动运动也被考虑进轨道动力学方程中,且系绳以第2节中的周期解为初始摆动状态。第2节显示,对于相同的轨道元素,摆动角θ和φ的幅度均随着ε的增大而增大。因此,项-Bzcosθcosφ的绝对值随着ε的增大而减小,从而造成T的幅值随着ε的增大而减小。而T与ζ的关系为正比例关系。因此,Ta与ε呈反比例关系,与ζ呈正比例关系。其中,ε对Ta的影响表示了系绳的摆动对Ta的影响。而Ta的变化趋势则可反映降轨时间的变化趋势。下面通过仿真算例来研究系统参数对轨道动力学的影响。
2.2 系统参数对轨道动力学的影响仿真
首先,在考虑了系绳摆动情况下,对运行于椭圆轨道上的电动力绳系的降轨过程进行仿真。本算例中,选取的系统参数的值与表1中所示相同;初始近地点高度为800 km,目标近地点高度为500 km,初始轨道偏心率为0.1,初始轨道倾角为25°。系绳的初始摆动状态为对应于系统参数和初始轨道元素的周期解,降轨过程中对应的状态则由摆动动力学方程积分得到。图4给出了降轨过程中轨道近地点高度、偏心率及轨道倾角随时间的变化关系。图5给出了降轨期间系绳面内和面外摆动角的变化。
图4显示,电动力绳系的降轨过程需要约9天的时间。在降轨过程中,轨道偏心率呈增大趋势,轨道倾角呈减小趋势。但是与近地点高度的明显变化相比,这两个轨道元素的变化幅度均很小。
图5显示,降轨过程中电动力绳系的摆动周期约为1.5~2.0 h。在仿真过程中,绳系的摆动考虑了轨道元素的变化,即图5中摆动角的计算中计入了轨道元素的实时变化。在摆动动力学方程(2)中,轨道近点高度的变化对该方程没有影响,只有轨道倾角和轨道偏心率的变化对周期解产生扰动。在一个摆动周期内,图4中的轨道倾角变化约0.00375°,轨道偏心率变化约0.0000225;即在整个降轨过程中,轨道偏心率和轨道倾角的变化非常小且非常缓慢。虽然周期解是不稳定的,但图5的结果显示,在降轨过程中轨道元素存在小的扰动下,绳系在长时间内仍然为近似周期摆动。这也反过来说明,在单独研究系统的摆动动力学过程中将轨道元素假设为不变是合理的。

图4 轨道近地点高度、偏心率及轨道倾角随时间的变化关系Fig.4 Time histories of the orbital altitude of the perigee, eccentricity and inclination of EDT during deorbit

图5 降轨期间摆动角的变化Fig.5 Time histories of the in-plane and out-of-plane libration angles during deorbit
然后,利用仿真算例来研究各系统参数对轨道动力学的影响。目前电动力绳系最主要的应用是对废弃卫星进行降轨,降轨效率是最重要、最需要考察的因素,轨道高度是最明显的变化量。因此,本文中仅关注近地点高度的变化,用系统的近地点高度从800 km降到500 km所耗时间来衡量降轨效率。
图6给出了降轨时间随各系统参数的变化关系。各子图中横坐标为所研究的系统参数的变化范围,而其余参数的值与表1中所示相同。所有的仿真中,初始的e和i设为e=0.1,i=25°;且在飞行过程中考虑绳系的摆动。初始的摆动状态则为对应于初始e,i及ε的周期解。
图6(a)显示,降轨时间随m1的增大而增大。m1的增大导致摆动动力学方程中的ε增大,在轨道动力学方程中,ζ的值随m1的增大而减小,因此分别正比于ζ和反比于ε的Ta的值随着m1的增大而减小;在减小的Ta作用下,降轨过程中的da/dt的绝对值减小,即降轨效率变慢。图6(a)中结果说明,增长的m1对系统的轨道动力学具有消极的影响。

图6 降轨时间随各系统参数的变化关系Fig.6 Values of deorbit time as functions of system parameters
图6(b)显示,降轨时间随m2的增大先减小后增大。这是因为随着m2的增大,摆动动力学方程中ε的值减小;而轨道动力学方程中ζ的值则随着m2的增大而减小;这两个因素导致Ta的绝对值随着m2的增大先减小后增大。Ta的绝对值越大,降轨效率越高,降轨时间越短;Ta的绝对值越小,降轨效率越低,降轨时间越长。图6(b)中的结果说明,增长的m2对系统的轨道动力学的影响为先积极后消极。
图6(c)显示,降轨时间随mt的增大而变短。这是因为随着mt的增大,摆动动力学方程中的ε减小,而轨道动力学方程中的ζ则增大,从而导致Ta的绝对值随着mt的增大而增大。图6(c)结果说明,增长的mt对系统的轨道动力学的影响为积极的。本质上,这是因为mt的增大意味着系绳的增长,从而提高了降轨效率。
3 讨 论
本节对系统参数对摆动动力学和轨道动力学的影响进行综合讨论,给出了关于每个系统参数的设计建议并提出了降轨策略。系统参数对摆动动力学和轨道动力学的影响总结于表2中。

表2 系统参数对摆动动力学和轨道动力学的影响Table 2 Summary of effects of the system parameters on libration dynamics and orbital dynamics
综合仿真结果可知,增长的m1对系统的摆动动力学和轨道动力学均有消极的影响。另外,增大的m1意味着发射成本的增加。因此,主星质量m1设计得越小越好。
而m2较小的增长就会造成摆动动力学不稳定性很大程度地降低,且在所有的系统参数中,增长的m2对于减小周期解的不稳定性效果最为明显。尽管增长的m2对于轨道动力学的影响为先积极后消极,但是最长的降轨时间与最短的降轨时间的差仅仅为3天,相较其他参数对降轨动力学的影响,是非常小的。相比其对摆动动力学的积极的影响,其对轨道动力学消极的影响可以忽略。另外,能够对摆动动力学产生明显效果的增长的m2也仅仅几千克的量级,这对于发射成本的产生的影响也比较小。因此,综合考虑,当进行系统设计时,子星质量m2越大越好。
mt的增长对系统的摆动动力学和轨道动力学均有积极的影响。其中,随着mt的增长降轨时间明显减少。mt的增长对降轨动力学产生的影响相对较小,在考虑发射成本时可以忽略。但是,mt的增长意味着系绳长度的增加,这样就增加了系统的展开难度。因此,在不影响系统展开的前提下,系绳的质量mt设计得越大越好。
电动力绳系最主要的功能是进行降轨,因此有必要综合考虑各种对降轨产生影响的因素,对应于降轨的整个系统进行设计,并提出合理的降轨策略。
在进行系统设计时,主星的质量设计要尽量小;子星的质量设计在满足发射成本约束、质量小于主星质量约束以及其它约束的情况下,质量尽可能大;绳系长度的设计则是在满足展开机构约束条件下,长度尽可能长。三个因素中,绳系长度的变化对降轨的影响最为明显,且最具有可行性,因此,在进行系统设计时,绳系的长度为最主要的设计变量。
在降轨过程中,绳系中的电流和绳系的姿态摆动均对系统的轨道动力学具有影响。因此,降轨策略的制定需主要考虑这两个因素。首先,由于常值电流情况下,系统存在规律的周期姿态摆动,因此降轨过程中需将绳系中电流控制为常值。而常值电流的大小则需要综合考虑姿态摆动的不稳定性以及电流产生能力来确定。在满足稳定性控制等约束范围内,电流的值越大越好。当系统的各组件质量、绳系中的电流大小确定后,以对应的周期解为初始摆动状态。在运行的过程中,当干扰力和轨道元素摄动等因素使得绳系的摆动偏离周期解达到一定的程度时,对绳系的摆动进行控制,使其回到此时对应的周期解上。绳系摆动的控制可通过控制绳系中的电流,或者安装在子星上的小推力发动机等方法实现。当绳系摆动恢复到周期解上时,停止控制;而当绳系摆动再次偏离周期解达到一定程度时,再次施加控制,这样直到降轨过程完成。
4 结 论
本文研究了主星质量、子星质量、系绳质量以及系绳中的电流对电动力绳系摆动动力学和轨道动力学的影响。通过各系统参数对周期解不稳定性的影响研究了系统参数对摆动动力学的影响。通过各系统参数对降轨时间的影响研究了系统参数对轨道动力学的影响。分析结果表明:主星质量的增大对摆动动力学和轨道动力学均有消极的影响;子星质量的增大对摆动动力学具有积极的影响,而对轨道动力学的影响则为先积极后消极;系绳质量的增大对摆动动力学和轨道动力学均有积极的影响;增大的电流对摆动动力学具有消极的影响,而对轨道动力学则有积极的影响。综合考虑各参数对系统摆动动力学和轨道动力学的影响程度,以及实际的发射、空间的展开等因素,可为各系统参数的设计以及降轨策略的制定提供理论参考和建议。

