肋骨许用应力对环肋圆柱壳结构设计的影响

李生，汪志强，殷洪

1 海军驻武汉地区第三军事代表室，湖北 武汉 430205

2 武汉第二船舶设计研究所，湖北 武汉 430205

0 引 言

加筋圆柱壳广泛应用于航空航天、船舶与海洋工程等领域，潜艇的主体也采用环肋圆柱壳结构。为了使潜艇圆柱壳结构性能更好，通常会基于相关设计规范[1]对潜艇圆柱壳结构进行优化。

针对上述问题，国内有学者对圆柱壳结构优化进行了相关研究。例如：丁海旭等[2]采用逼近目标规划（approximate goal programming）模型对圆柱壳进行优化，结果表明肋骨应力易达到许用值标准，而其它属性相对于许用值仍有较大的裕度，并指出规范应放宽肋骨的许用值标准；李学斌[3]采用分支定界法(branch-and-bound method)对圆柱壳的重量进行单目标优化，优化结果及更多算例都表明肋骨约束为主要设计约束；潘治等[4]采用多岛遗传算法（multi-island genetic algorithm,MIGA）对圆柱壳的重量进行单目标优化，结果表明，设计约束条件为强度、稳性和频率约束，且对优化结果进行分析还发现，肋骨的应力已非常接近于许用值，而其它指标仍有一定的储备。可见，上述研究均得出了肋骨许用应力是圆柱壳结构优化设计的主要约束条件，也指出了应放宽肋骨许用应力的观点，但尚未深入分析不同肋骨许用应力对圆柱壳结构设计的影响，鉴此，本文将建立基于综合裕度（加权和法）（weighted-sum method）的环肋圆柱壳多目标优化模型，采用宽容度排序法（tolerance ranking method）对模型进行优化求解，分别讨论肋骨许用应力对结构和宽容度（裕度）排序法中各属性裕度对优化结果的影响。

1 理论分析

1.1 强度和稳性分析

图1所示为潜艇的典型舱段。图中，L为舱段长度，l为肋骨间距，h为壳板厚度，R为圆柱壳中面半径，e为肋骨对壳板中面偏心距，坐标x，z，θ分别表示圆柱壳的轴向、径向和周向。

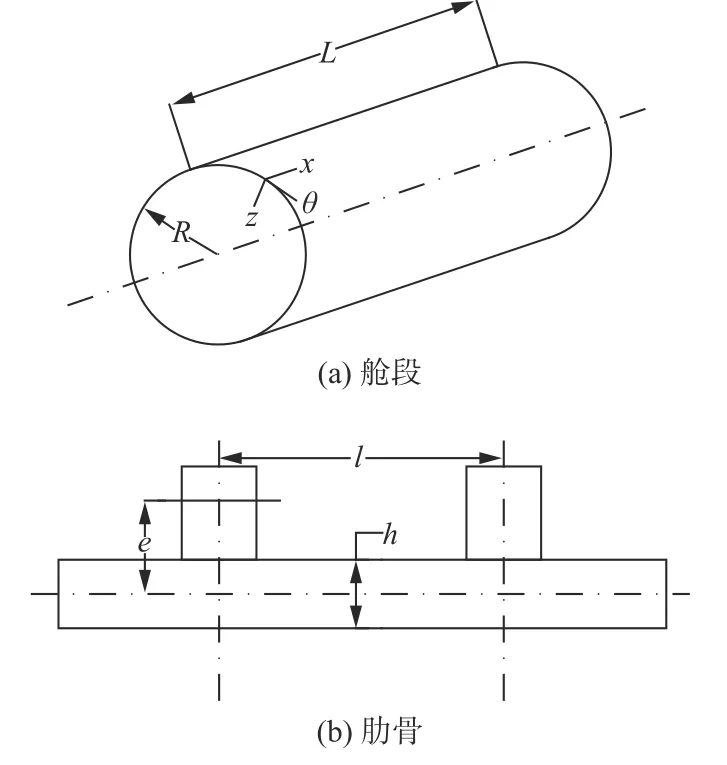
图1 典型舱段的环肋圆柱壳结构示意图Fig.1 Schematic diagram of ring-stiffened cylindrical shell structure for a typical compartment

式中：p为计算深度处的静水压力；系数K1，K20，Kl以及其它辅助函数详见文献[5]。

在静水压力下，若圆柱壳肋骨的刚度超过其临界刚度，肋骨间的壳板首先失稳。式（2）为局部壳板失稳的理论临界载荷pE的计算公式[5]。

式中：m为失稳时轴线方向的半波数；I为计及带板的肋骨惯性矩； λ′=πR/L。

对计算的局部壳板失稳压力和整体壳板失稳压力的理论临界值分别进行修正，如下所示。

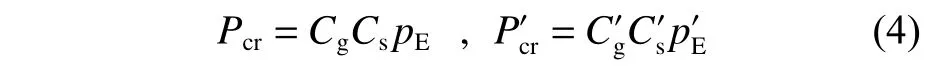
式中：Cg,Cg′分别为圆柱壳局部板壳失稳及整体失稳时的几何非线性修正系数；Cs,Cs′分别为圆柱壳局部板壳失稳及整体失稳时的材料物理非线性修正系数。计算过程中，需要使用设计图谱，故本文采用了一维三次样条插值法进行求解。

对于圆柱壳结构重量，计算公式如下：

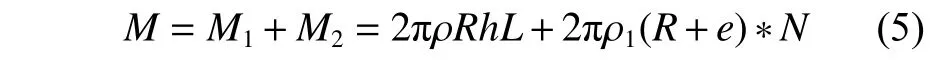
式中：M1，M2分别为圆柱壳重量和肋骨重量；ρ为壳板材料密度；ρ1为肋骨单位长度的重量；N为肋骨数量，肋骨为外肋布置；R+e为肋骨的中性轴半径。

按照GJB/Z 21-91《潜艇结构设计计算方法》[1]规范要求，校核3个应力和2个临界失稳压力的标准，如式(6)所示。

式中，σs为材料屈服极限值。

1.2 基于综合裕度的多目标优化模型

文献[3]将属性计算值相对于许用值裕度与许用值间的比值称为属性裕度。因此，将3个应力裕度经加权合成为综合应力裕度g1，具体如下：

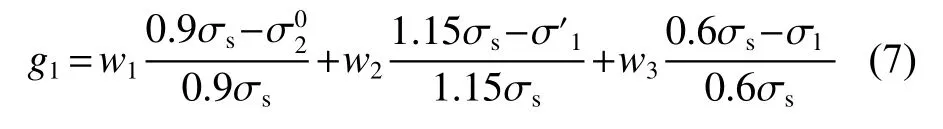
式 中：w1,w2,w3为 应 力 裕 度 加 权 系 数，w1+w2+w3=1。

对于局部和整体壳板失稳压力这2个临界载荷，经裕度加权合成为综合临界载荷裕度，即

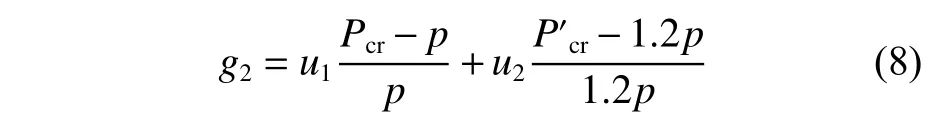
式中：u1,u2为 临界载荷裕度加权系数，u1+u2=1。

通过对圆柱壳各属性裕度（包括3个应力属性裕度和2个临界载荷属性裕度）进行约束，使各属性裕度之间更均匀，则有：

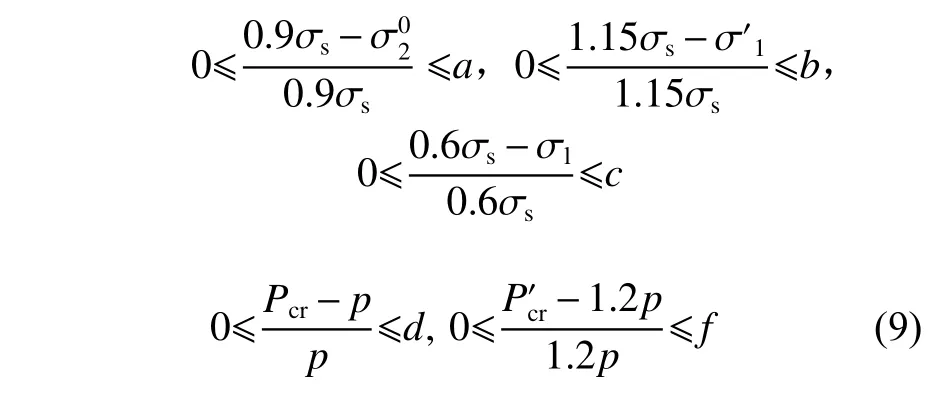
式中，a,b,c,d,f为各属性裕度约束的上限，其值根据可行解空间内各属性的统计特性来确定。

本文采用信息熵法（information entropy method）计算各属性裕度的权重。信息熵方法是一种客观赋权法，根据指标提供信息量的大小来确定指标的权值[6]，信息熵法所需的决策矩阵用全因子试验设计法(full factorial experimental design)获取。全因子试验设计方法指全部因子的所有水平的所有组合都至少进行一次试验[7]。因此，对于离散变量问题，采用全因子试验设计方法能够得到所有可行解。

本文讨论的基于综合裕度的多目标优化模型包括3个目标函数（ maxg2， ming1，M）、5个设计变量（ 舱段长度L，肋骨间距l，壳板厚度h，圆柱壳中面半径R和肋骨型号cn）、2种约束条件（变量约束和裕度约束）。其中，2种变量约束的取值应分别遵循： 1）变量约束：h按照CB/T 3432-1992《船用钢板尺寸和重量》[8]标准选取，l按0.05 m的倍数递增，cn按照CB/T 3433-1992《船用对称型钢尺寸、外形、重量及允许偏差》标准[9]选取。为了方便建造，R和L都采用整型规格。2）裕度约束：按照式（9）所示取值。

1.3 求解方法

采用宽容度排序法[10]进行求解。宽容度排序法先将q个目标按相对重要度进行排序，然后按顺序逐层进行单目标优化。将第j层属性单目标优化的最优值fj′适当放宽形成约束后，加入到j+1层单目标优化的约束条件中，逐层优化直至最后一层，即可得到最优解[10]。计算的具体步骤如表1所示。

表1 宽容度排序法的计算过程Table 1 Computing process of tolerance ranking method

对于宽容度排序法每层的单目标优化，采用改进的快速非支配排序遗传算法NSGA-Ⅱ[11]进行优化求解。

2 算例及讨论

2.1 典型环肋圆柱壳数值分析

本节以某典型舱段的环肋圆柱壳为例，对属性裕度进行数值分析。材料参数如下：弹性模量E=1.96×105MPa，泊松比µ=0.3，材料屈服极限值σs=590 MPa。设计变量的取值范围如表2所示。

根据表2设计变量取值范围，使用mode-FRONTIER 4.5.0软件并采用全因子试验设计方法，得到满足式（6）的约束可行解共2 757个。图2 所示为各属性裕度的统计结果。

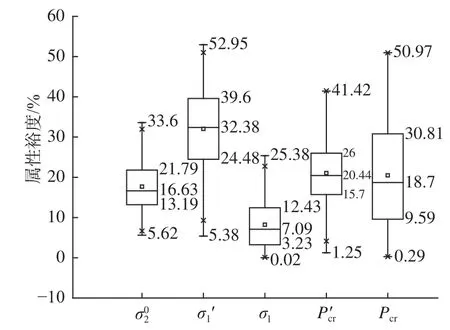
图2 可行解的各属性裕度统计盒式图Fig.2 Box plot of margins of each attribute value for feasible solutions

表2 典型舱段环肋圆柱壳结构设计变量取值范围Table 2 Range of design variables of ring-stiffened cylindrical shell structure for a typical compartment

根据图2中的统计特性，可见，裕度范围大的属性需加强约束（例如σ′1，Pcr），而裕度范围小的属性约束需稍微放宽（例如σl）。为使各属性裕度范围间更均匀，且保证约束范围内有一定量的可行解，表3给出了设定的各属性裕度约束范围。

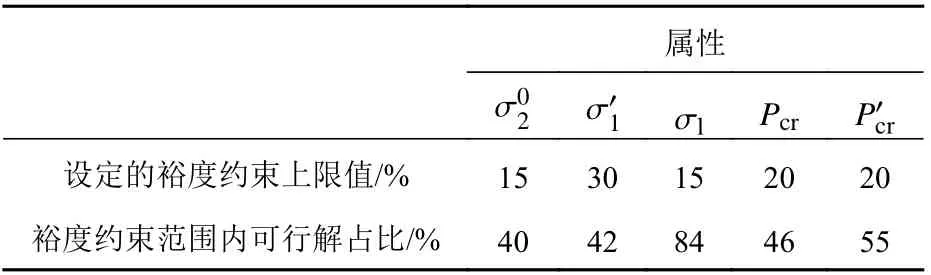
表3 各属性裕度约束范围及可行解的占比Table 3 The constraint range of margins of each attribute value and proportion of feasible solutions

根据表3中的各属性约束的上限值，可以将式（9）进行如下转化：

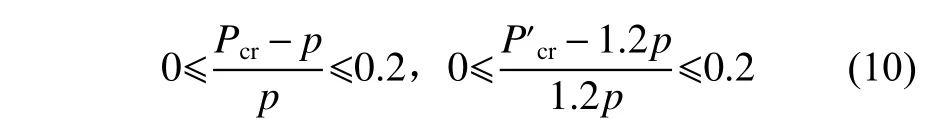
以式（10）为约束条件，从采取全因子试验设计方法获取的2 757个约束可行解中筛选得到576个可行解，利用这576个可行解按式（11）将环肋圆柱壳各属性转化为裕度值，从而得到关于属性裕度的数据集合。

式中，w02，w′1，wl为应力的裕度值；wcr，w′cr为临界载荷的裕度值。

首先，采用信息熵法计算生成的属性裕度值，得到3个应力裕度和2个临界载荷裕度的加权系数，并将式（7）和式（8）转化为：

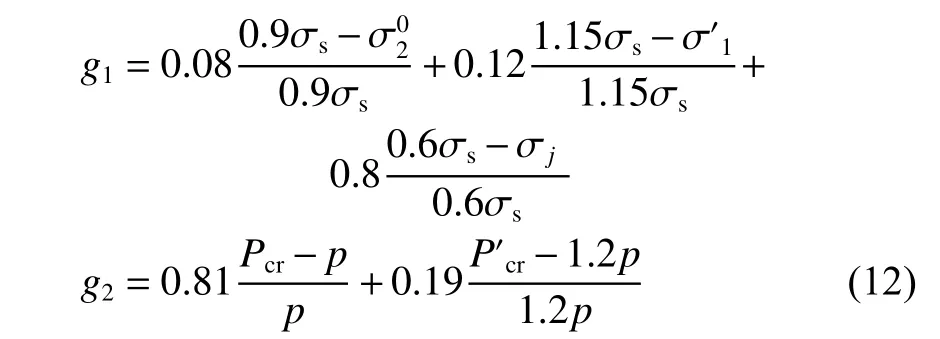
然后，再根据576个可行解，采用信息熵法计算得到综合应力裕度g1、综合临界载荷裕度g2及重量的权重分别为0.426，0.434和0.14。根据3个目标的客观权重，按重要度作如下排序：

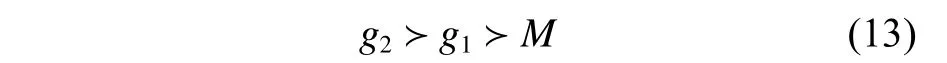
设综合临界载荷裕度g2的宽容度为10%，综合应力裕度g1的宽容度为8%，得到如表4所示最优解。

表4 最优解Table 4 The optimum solutions（g1-8%, g2-10%）

根据表4，σj的裕度为2.94%，其它属性的裕度均大于13.51%，肋骨应力几乎达到许用值，其它属性还有较大的裕度。由此可见，采用宽容度排序法得到的最优解与文献[2～4]得到的结论是一致的，肋骨应力为主要的约束。

2.2 肋骨许用应力对优化结果的影响分析

本文对肋骨许用应力对优化结果的影响进行理论探讨。设肋骨许用应力为xfσs，系数xf取值分别如表5所示，其它各属性的许用值不变。

为方便计算，约束范围与式（9）相同。按不同肋骨许用应力系数xf的取值，分别进行全因子试验设计，共获得7 599个可行解，然后采用信息熵法计算得到2种综合裕度的加权系数为：

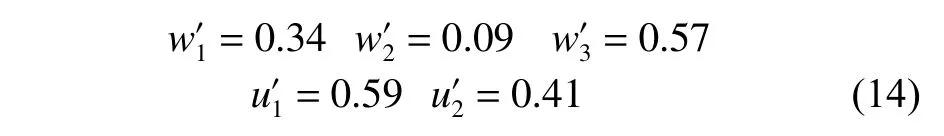
采用信息熵法计算得到综合应力裕度g1、综合临界载荷裕度g2以及重量的客观权重分别为0.25，0.62，0.13。该3个目标的重要度排序与式（11）相同。同样地，综合临界载荷裕度g2的宽容度取为10%，综合应力裕度g1的宽容度取为8%，得到如表5所示的不同肋骨许用应力对应的最优解。

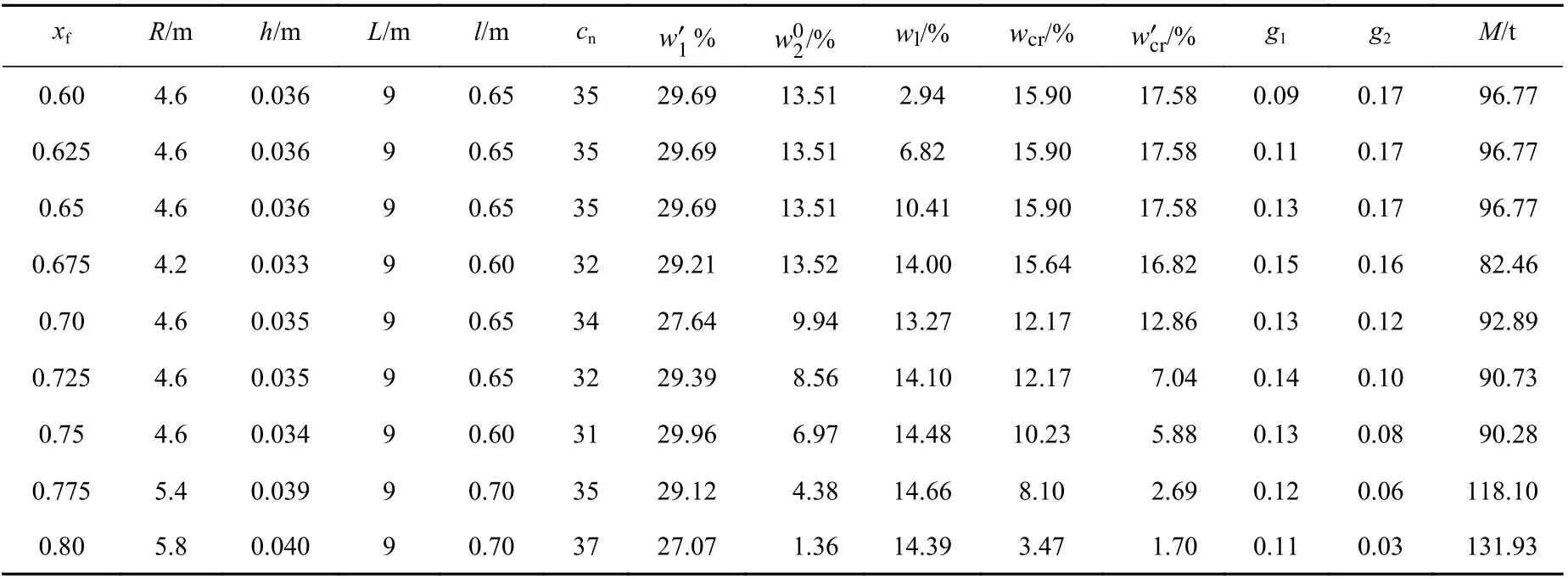
表5 不同肋骨许用应力对应的最优解（g2-10%，g1-8%）Table 5 The optimum solutions of different allowable stress of ribs（g2-10%，g1-8%）

根据表5，随着系数xf的增加，σ′1的裕度值并没有太大的变化，且都接近设定的裕度约束上限的30%。此外，当xf>0.675时，σ02与2个临界载荷的裕度值都随着xf的变大而减小，随着xf的增加，σj的裕度值也随之增加；当xf>0.675时，肋骨应力的裕度接近设定的裕度约束上限的15%；当xf=0.675时，除σ′1的裕度较大外，其它属性的裕度值都已非常接近，即均约15%，结构属性裕度之间已较均匀，且结构重量也相对较小。

由此可见，适当放宽肋骨的许用应力值，能够解决最优解肋骨应力裕度小的问题，且还能够使最优解的各属性裕度之间更均匀。然而，肋骨许用应力值也并非越大越好，xf在0.65～0.7之间时的优化结果则比较好。

由表5还可见，当xf<0.75时，最优解的σ，σ以及2个临界载荷的裕度值都较大。这里，尝试通过改变2个综合裕度的宽容度，来观察其对优化结果带来的影响。

设综合临界载荷裕度g2的宽容度为30%，综合应力裕度g1的宽容度为15%，得到的优化结果如表6所示。进而，设综合临界载荷裕度g2的宽容度为40%，综合应力裕度g1的宽容度为20%，得到的优化结果如表7所示。

对比表5，表6和表7可以看出，放宽综合临界载荷裕度g2以及综合应力裕度g1的宽容度后，最优解的综合临界载荷裕度和综合应力裕度的值都有所降低，对应的2个临界载荷的裕度值有所降低，3个应力的裕度值也有相应的减小，圆柱壳结构重量M也有所减小。放宽临界载荷裕度和综合应力裕度的宽容度值后，最优解对临界载荷的偏重（偏重指接近属性理想值的程度）降低了，而对应力和重量的偏重增加了。可见，在宽容度排序法中各属性的宽容度值对属性的偏重有重要影响，因此，可以通过调节各属性宽容度值来得到想要的最优解。

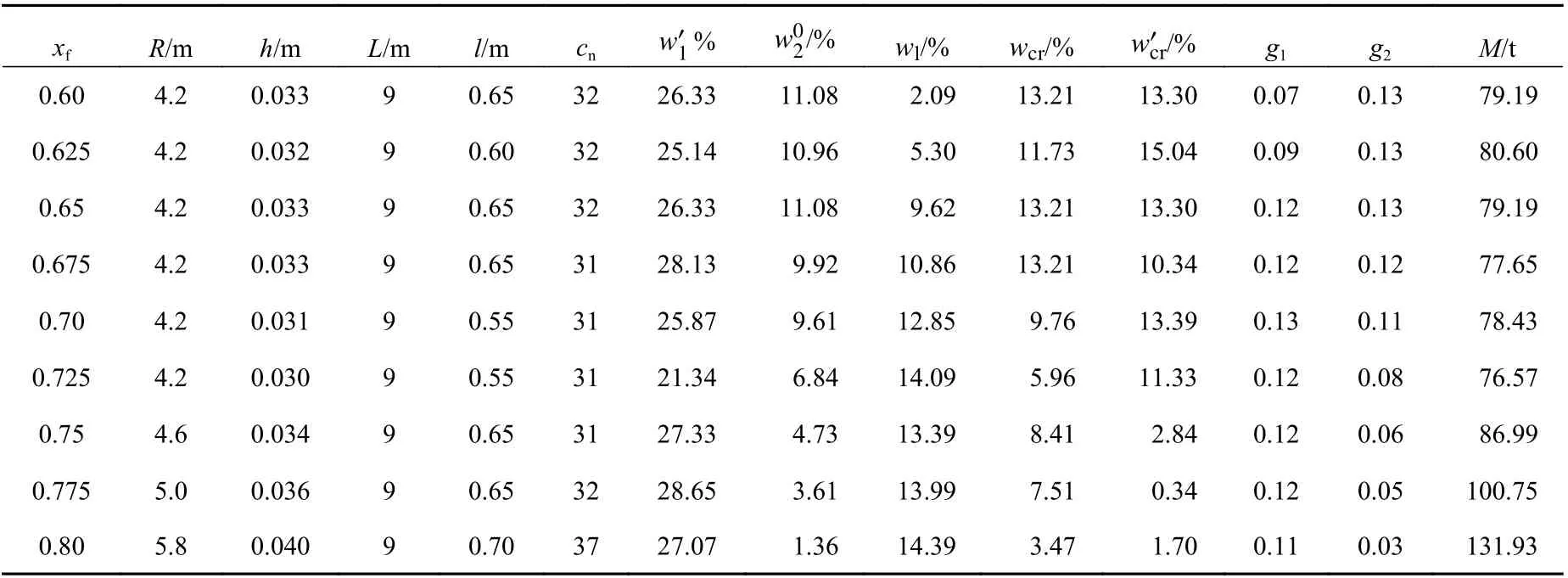
表6 不同肋骨许用应力对应的最优解（g2-30%，g1-15%）Table 6 The optimum solutions of different allowable stress of ribs（g2-30%，g1-15%）

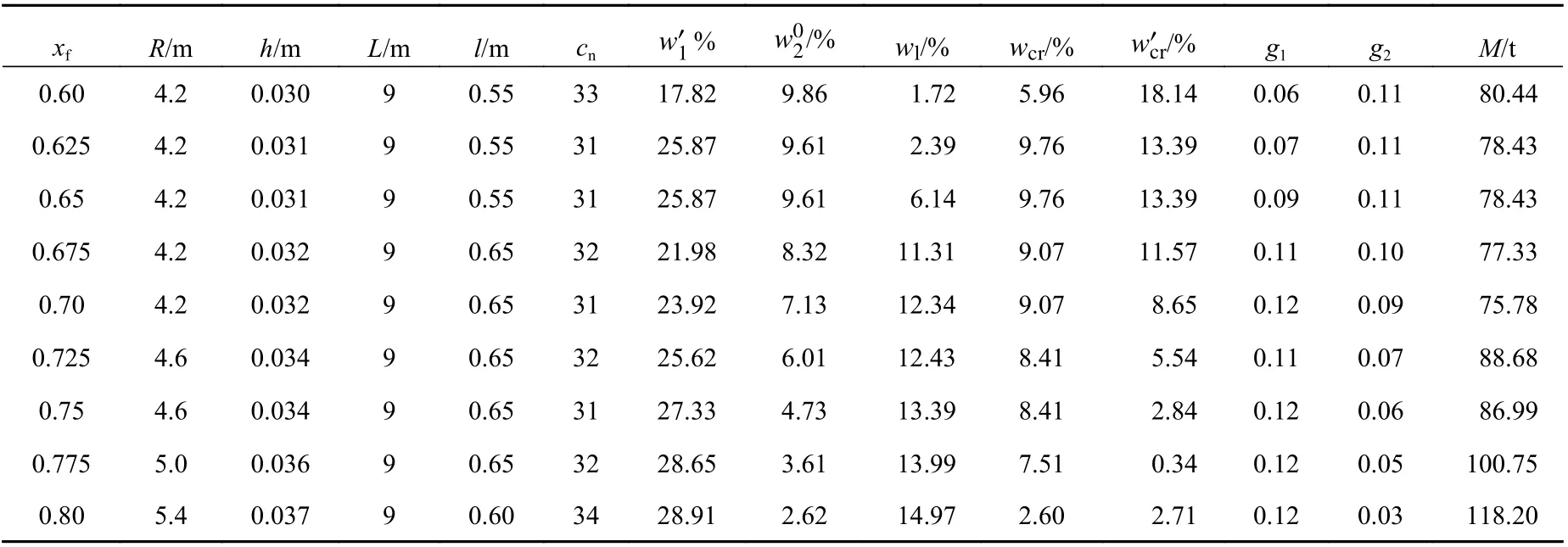
表7 不同肋骨许用应力对应的最优解（g2-40%，g1-20%）Table 7 The optimum solutions of different allowable stress of ribs（g2-40%，g1-20%）

3 结 论

本文采用宽容度排序法基于综合裕度的环肋圆柱壳多目标优化模型对圆柱壳强度和稳性裕度之间不均匀的问题进行了研究， 讨论了肋骨许用应力及其各属性的宽容度值对优化结果的影响，并得到如下结论：

1） 按3个目标的客观权重，得到其重要度排序为：g2≻g1≻M。

2） 基于规范的许用应力值，采用宽容度排序法优化得到的最优解的肋骨应力裕度小，其它属性的裕度较大，肋骨应力为主要的约束条件。

3） 通过适当放宽肋骨许用应力来研究肋骨许用应力对结构设计的影响，得到的结果显示，放宽肋骨许用应力能够解决肋骨应力裕度小的问题，但是肋骨的许用应力并非越大越好，这可为未来规范的修正更新提供设计参考。

4） 放宽临界载荷裕度和综合应力裕度的宽容度值后，最优解各属性对临界载荷的偏重降低了，而对应力和重量的偏重增加了。这说明在宽容度排序法中，可以通过调节各属性宽容度的值得到不同的最优解。