喷水推进器进口流道水动力性能分析

邱继涛，尹晓辉，王仁智

1 喷水推进技术重点实验室，上海 200011

2 中国船舶及海洋工程设计研究院，上海 200011

0 引 言

喷水推进器在高航速下具有效率高、抗空化能力强等特点，因此被广泛用于高速船舶。喷水推进器主要包括进口流道、喷水推进泵及喷口3个过流部件，其中，进口流道设计的好坏对喷水推进器能否发挥出优良的性能有着重要影响。一方面，泵进口流场的均匀性将直接影响泵的水动力性能和汽蚀性能等，而进口流道的构型则决定了泵进口流场的特性；另一方面，进口流道的设计需要考虑运行工况的适应性，不合理的设计会增加过流损失，导致推进器的效率降低。

随着计算流体动力学（CFD）的快速发展，CFD技术在喷水推进器进口流道设计、性能分析以及其他方面的运用日益广泛[1-2]。史俊等[3]采用RANS方法和SST湍流模型，研究了不同进口长度流道模型在不同进速比条件下进水流道内部流场的流动特征，结果显示，适当增加进水流道的进口长度有助于改善进水流道的流动性能。李臣等[4]采用RANS方法和RNGk-ε湍流模型研究了不同进流角流道模型的内部流动特征，计算结果表明，在模拟的进速比条件下，随着流道倾角的增大，流道内的流场特性变差。汲国瑞等[5]研究了进口流道唇口形状对出口流动不均匀度和唇口驻点位置的影响，得出了其影响规律，结果对进口流道唇口设计具有指导意义。杨福芹等[6]对喷水推进器进水流道的参数予以了分析，研究表明，进水流道管径对出口流场的不均匀度、叶片的汽蚀和喷口速度影响较大; 进水流道的优化改进应适当考虑进水流道管径，以提高其工况适应能力。目前，针对喷水推进器进口流道水动力性能的研究相对较少，且大多为CFD数值研究，而对于CFD数值模拟，其可靠性尤为重要，因此有必要对数值模拟进行不确定度分析；另外，影响进口流道水动力性能的主要参数不唯一，因此需要进行多参数综合研究。

工程实践表明，影响进口流道性能的主要几何参数为轴线高度和进流角度。因此，本文拟采用CFD技术，研究不同进速比工况下进口流道轴线高度和进流角对出口流场不均匀度的影响，以及流道本身的流动损失（流动损失通过流道效率来评价），然后根据ITTC推荐的不确定度分析规程[7-8]进行数值不确定度分析。

1 进口流道水动力性能数值模拟方法

本文采用RANS方法对进口流道进行水动力性能模拟，进口流道几何参数的定义和计算域模型分别如图1和图2所示。图中：D为进口流道出口直径；H为轴线高度，即出口中心线（轴线）至船底的距离；α为进流角，即进口流道倾斜段与船底的夹角。进口流道距上游进口40D，距下游出口20D，计算域宽度为10D，深度为8D。上游进口为速度进口，下游出口为压力出口，进口流道出口为质量流量出口，计算域侧面和底面为对称平面，其他边界为不可滑移壁面，参考压力为大气压，通过改变流道出口的流量Q来实现多工况数值模拟。

图1 进口流道几何参数定义Fig.1 Definition of geometric parameters of inlet duct

图2 计算域模型Fig.2 Computational domain model

本文采用STAR-CCM+商业软件进行定常RANS模拟，采用Realizablek-ε 两层湍流模型对控制方程进行封闭，采用全y+方式处理壁面流动，以使该求解适应低雷诺数情况（y+≈1）以及使用壁面函数的高雷诺数情况（y+>30）。控制方程采用二阶离散格式，压力−速度耦合计算选用SIMPLE算法。

进口流道水动力性能参数的定义方法如下：选取一个控制体研究进口流道的效率和出口流动的不均匀度，该控制体的出口为进口流道的实际出口，进口为流道前部与船底交点前1D处的半椭圆型截面，亦称获流面[9]，该截面与轴线垂直，其面积根据对应工况下的流线确定，同时要保证进、出口流量相等，如图3所示。

图3 控制体进口与出口Fig.3 The inlet and outlet of control body

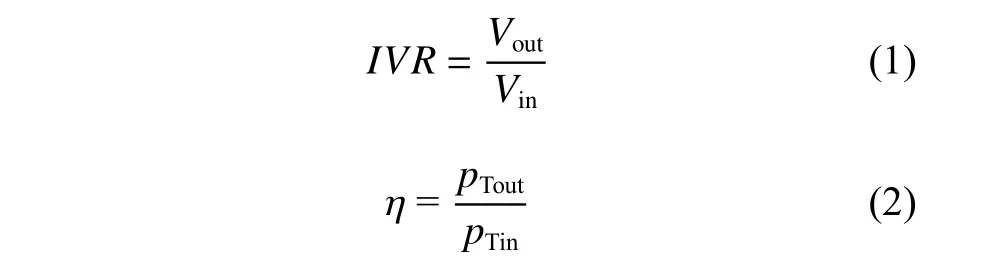
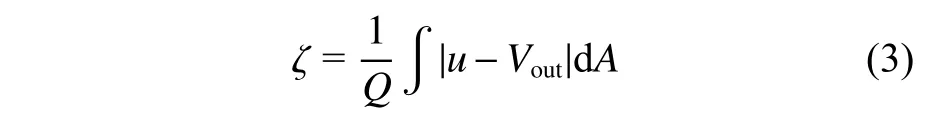
进速比IVR、进口流道效率η和出口流动不均匀度ζ的定义为：以上式中：Vin为自由来流速度，m/s；Vout为进口流道出口的平均速度，m/s，其方向均为轴向；pTin和pTout分别为控制体进口和实际出口的总压（不含大气压），Pa；Q为出口流量，m3/s；u为控制体出口的轴向速度，m/s；dA为出口面积微元。

2 不确定度分析

本文中进口流道出口直径D=200 mm，选取H=1.0D，α=33°，IVR=0.7（自由来流速度Vin=10 m/s，进口流道出口流量Q=0.22 m3/s）的工况对模拟的η和ζ进行边界合理性研究及不确定度分析。

采用六面体结构化网格对计算域进行离散，中细纵化剖比面（rG网=格拓）扑划如分图粗4、所中示、细。采3套用网相格同进的行网不格确定度分析。3套网格的主要参数如表1所示。

图4 中纵剖面网格拓扑Fig.4 The grid topology of mid-section

表1 网格主要参数Table 1 The main parameters of grid

因船底板的黏性作用，流道进口一般被船底板边界层覆盖。本文使用固定的壁面（长度为40D）替代流道进口前的船底板结构。该固壁面长度若过小，可能会导致流体沿船底板到达流道进口时边界层未完全发展而影响模拟结果，故有必要对船底固壁长度的合理性进行验证。图5给出了距上游边界入口不同站位处的速度分布。从图示结果来看，可认为当来流到达37D站位（距流道进口3D）时边界层已完全发展，对计算结果的影响可忽略，可见本文的边界长度设置合理。

图5 船底不同站位处的速度剖面Fig.5 Velocity profiles at different stations on the bottom

不确定度分析采用Richardson外推法，过程参见文献[7]，此处不再赘述。η和ζ的不确定度计算结果如表2所示，其中的百分数以细网格的数值结果为基准，η的模拟结果为振荡收敛，ζ的模拟结果为单调收敛。因η的数值解呈振荡收敛状态，故其不确定度结果相对较小；ζ的数值不确定度较大，不过均小于4%，这表明本文网格的收敛性良好。后续的计算将采用细网格，对应于表1中的网格高度，y+≈5。

表2 不确定度计算结果Table 2 Uncertainty calculation results

3 进口流道水动力性能分析

进口流道内的损失根据形式的不同可以分为沿程损失和局部损失2种。在流体流动过程中，液体分子之间以及其与流道之间会产生摩擦，为克服摩擦而引起的能量损失称为沿程损失。而因流道轮廓外形或流动方向的急剧变化而产生的流体能量下降则称为局部损失。进口流道构型的改变会引起流道损失的变化，本文将通过研究不同H和α对η和ζ的影响。H的变化（α不变）主要影响沿程损失；α的变化（H不变）既影响沿程损失，又影响局部损失。计算工况为：Vin=10 m/s，Q=0.16，0.22，0.28，0.35，0.41 m3/s分别对应进速比IVR=0.5，0.7，0.9，1.1和1.3。

3.1 不同工况下轴线高度对水动力性能的影响

本节研究不同工况下轴线高度H对流道水动力性能的影响。共设置5个轴线高度，分别为H=0.8D，1.0D，1.1D，1.3D，1.5D(D=200 mm)，α=33°。图6所示为不同轴线高度下进口流道的水动力性能曲面图（为展示方便，坐标轴方向未统一）。由图可知，随着IVR变大，亦即流道内流速的增大，η是先变大而后略有减小，最高效率点在IVR=0.9附近；ζ随着IVR的变大迅速减小，且减小幅度是逐渐变小的；随着H的增大，η呈现出下降的趋势，IVR越小，η下降越缓慢，在IVR=0.5处效率有所上升；ζ的变化趋势平缓，只在IVR=0.5时呈现出下降趋势。H的增大会导致沿程损失增加，故η会有所下降；而在小IVR工况下，增大H实际上是增加流道过流长度，这有利于改善出口流动的不均匀度，因此η略微上升。

图6 不同轴线高度H下进口流道的水动力性能Fig.6 Hydrodynamic performance of inlet duct at different H

3.2 不同工况下进流角对水动力性能的影响

本节研究不同工况下进流角α对流道水动力性能的影响。共设置4个进流角，分别为α=21°，27°，33°，39°，H=1.0D。图7所示为不同进流角下进口流道的水动力性能曲面图（为展示方便，坐标轴方向未统一）。由图可知，随着IVR变大，η是先变大后变小，最高效率点在IVR=0.9附近，当α较 小（α=21°，27°）时，η下 降 较 大；ζ随着IVR的变大迅速减小，且减小幅度逐渐变小。初步分析，这是因为随着进口流道内流速的增大，边界层变薄，由摩擦引起的沿程损失占流道内总能量的比重减小，导致η上升，且出流更加均匀；但随着流速的进一步增大，流道内的局部损失相对增加，因而η也会有所下降。

图7 不同进流角进口下流道的水动力性能Fig.7 Hydrodynamic performance of inlet duct at different α

随着α的增大，η呈现出下降的趋势，IVR越大，η下降越缓慢，当IVR=1.3时，η有所上升；而ζ则呈上升趋势，且IVR越小其上升速度越快。随着α的增大，局部损失随之增加，因此ζ上升，从而导致η有所下降；但在高IVR工况时，流体向上的分量较大，此时较大的α将有利于进流，因此η略有上升。

3.3 进口流道流场分析

选取H=1.0D，α=27°；H=1.0D，α=33°；H=1.3D，α=33°这3个进口流道对流场进行分析。图8～图10所示分别为不同IVR下进口流道中剖面的流线形态和压力云图。图11所示为进口流道出口截面内的速度分布图（从左到右分别为IVR=0.5，0.7，1.1，1.3工况），更直观地反映了出口流动的不均匀度。图11中：u/Vout−1为流道出口截面轴向速度的不均匀程度，代表的是云图，此值越接近于0，轴向流动越均匀；v/Vout为流道出口截面内速度的不均匀程度，代表的是矢量图，此值越小，流动越均匀，其中v为截面内的速度矢量的大小。由图8可知，随着IVR的增大，流体向上的速度分量增大，导致唇口处的驻点位置下移，因此当进流角α较小时，易在唇口处发生流动分离，从而在唇口上方形成低压区，严重时，还可能产生空化。比较图8（d）和图9（d）可知，增大进流角α可改善高IVR时唇口处的流动分离，但在低IVR工况（图9（a））下，进口流道背部会产生流动分离，从而使出口流动的不均匀度增大，图11（b）亦表明了这一点。此时，适当增加进口流道轴线高度H在一定程度上可以减少背部的流动分离，改善出口流动的不均匀度（图10（a）），且通过对比图11(b)和图11(c)的第1幅图亦可得出此结论。

图8 进口流道中剖面流线和压力云图（H=1.0D，α=27°）Fig.8 Streamlines and pressure contours at middle profile of inlet duct（H=1.0D，α=27°）

图9 进口流道中剖面流线和压力云图（H=1.0D，α=33°）Fig.9 Streamlines and pressure contours at middle profile of inlet duct（H=1.0D，α=33°）

图10 进口流道中剖面流线和压力云图（H=1.3D，α=33°）Fig.10 Streamlines and pressure contours at middle profile of inlet duct（H=1.3D，α=33°）

图11 进口流道出口截面内的速度分布Fig.11 The velocity profiles in the exit section of inlet duct

4 结 语

本文通过CFD数值模拟，分别对进速比IVR、轴线高度H和进流角α对进口流道效率、出口流动不均匀度的影响进行了分析。分别在保持α不变设置5个H，和保持H不变设置4个α，对上述模型在不同IVR（0.5～1.3）工况下的数值进行了模拟。

从水动力性能来看，当IVR=0.7～1.1时进口流道效率较高，对应的损失较小；在高效区内（IVR=0.7～1.1），取过大的H和α对效率及出口流动的不均匀度不利，实际上，当船速和主机功率已定时，根据IVR的选择即可确定出泵的工作状态。从流场特性来看，增大α能减小高IVR时唇口的流动分离；增加H可以改善小IVR时背部的流动分离。但是，H和α往往受布置空间的制约。综上，进口流道的参数设计需根据船、泵匹配后的工况在高效区内进行主参数的权衡选择。