湍流入流下泵喷推进器力谱特性研究

师帅康，黄修长*，饶志强，华宏星

1 上海交通大学 振动、冲击、噪声研究所, 上海 200240

2 上海交通大学 机械系统与振动国家重点实验室, 上海 200240

0 引 言

随着我国潜艇制造技术的日益发展，潜艇螺旋桨的振动与声辐射成为潜艇低噪声设计的重要研究对象。由入流湍流导致的螺旋桨运行时产生的非定常力是潜艇低频振动噪声的重要来源之一[1]。螺旋桨中的非定常脉动力谱由低频线谱和宽带随机谱构成，分别反映螺旋桨流场的空间不均匀性和时间非定常性[2]。对螺旋桨而言，叶片通过频率（blade passing frequency，BPF）（以下简称“叶频”）处的线谱周期性分量以及其谐波来自艇体附属物和由转子周期性转动形成的空间非均匀流场[3]，而入流湍流与螺旋桨相互作用产生的涡旋则导致非定常力宽带谱[4]。宽带力分量的能量分布在几赫兹至几百赫兹的宽频带上，会导致推进轴系和艇体产生随机振动，激发结构特征模态，从而在低频辐射噪声谱中形成声纹特征。因此，螺旋桨非定常力宽带谱受到研究人员的关注。

许多学者采用理论方法对螺旋桨非定常力宽带谱进行了预报。Sevik[5]采用相关性法研究了螺旋桨对随机速度脉动的响应，并将其应用到了各向同性均匀湍流入流下十叶螺旋桨的非定常力预报上。由于其仅考虑了来流速度对非定常力的影响，忽略了螺旋桨旋转的影响，所以其结果只能显示力谱的大致趋势，而不能预报叶频处非定常力的“驼峰”。Blake[1]利用频谱法建立了螺旋桨非定常力宽频谱公式，采用薄翼理论计算了压力面与吸力面之间的压差，并通过湍流波数谱和力响应函数对翼展方向上的压差求积分获得了力谱。Kirschner等[6]提出了一种数值积分方法，即将叶片在径向上分成几个条带，假设每个条带中的物理量保持不变，然后将采用该方法获得的结果与实验结果进行了比较，结果显示其一致性较好。Chen等[7-9]采用相关分析法和条带法成功获得了螺旋桨的非定常力宽带谱，其通过结合随机响应分析，获得了螺旋桨非定常宽带力及传递至轴系的传递率，分析了湍流参数和螺旋桨工作条件对非定常力宽带谱的影响规律。

在试验方面，Sevik[5]在水洞中研究了十叶螺旋桨在不同湍流尺寸下的非定常力，试验结果显示非定常力在叶频处出现了波峰，发现波峰值是随湍流积分尺度的增大而增大的。

另外，通过计算流体力学（CFD）仿真也可以获得螺旋桨的非定常宽带力谱。Tutar等[10]采用大涡模拟（large eddy simulation，LES）结合在入口施加随机扰动的算法，对高雷诺数下二维圆柱绕流进行了仿真，通过与实验结果的比较发现，该方法可以提高尾流流动的分辨程度，能很好地捕捉圆柱绕流涡脱落细节。Yao等[11]采用LES方法预测了十叶螺旋桨的非定常力宽带谱，并将结果与Sevik[5]的实验结果进行了比较，显示在低频段其结果与实验值的趋势相符，并计算出了以叶频为中心的“驼峰”。

泵喷推进器是一种组合推进器，由于其同时包含定子和导管，所以采用理论方法对其非定常力宽带谱进行预报比较困难。目前的研究是以获得线谱成分为主，例如采用雷诺平均法（Reynolds averaged Navier-Stokes，RANS）来获得泵喷推进器非定常力的线谱成分（如转子叶频、定子叶频、由艇体艉部十字舵导致的4倍轴频等）[12-13]。由于湍流的强非定常和随机属性，想要捕捉螺旋桨壁面边界层中的压力脉动特性，基于时间平均的RANS方法并不适用，因为采用RANS方法无法得到非定常力宽带成分，所以，急需对泵喷推进器在湍流入流下的非定常宽带力特性展开研究。

本文拟采用CFD方法，通过湍流生成栅格和频谱合成法相结合的方法，产生具有时间脉动和空间相干结构的湍流，并将该方法与LES相结合获得泵喷推进器非定常力的宽带谱，然后，再与仅有转子时（相当于螺旋桨）的非定常力宽带谱进行比较，分析泵喷推进器与螺旋桨非定常力宽带谱之间的差异以及其成因。

1 数值方法

1.1 大涡模拟

LES是介于直接数值模拟（direct numerical simulation，DNS）与RANS之间的一种折中的数值模拟方法，其通过空间滤波技术将不同尺度的涡分离开，只求解对压力脉动起主要作用的大尺度涡，过滤掉小的涡。相比DNS，LES降低了对计算资源的需求，而与RANS相比，LES又能获得更多的脉动信息。

LES的控制方程由连续性方程及通过滤波函数处理获得的非定常N-S方程组成：

式中：ρ为流体密度；P为流场中压力；xi和xj为笛卡尔坐标分量（i，j=1,2,3）；ui，uj分别为 与xi和xj相关联的速度分量；，为滤波后的平均速度分量；µ为流体的动力黏性系数；σij为由分子黏性引起的应力张量；δij为 克罗内克函数；τij=为亚格子雷诺应力，需要用亚格子模型进行封闭，本文采用Smagorinsky-Lilly[14-15]模型来模拟亚格子应力，见式（4），该应力反应了小规模脉动和分解尺度涡旋之间的动量传递[16-17]。

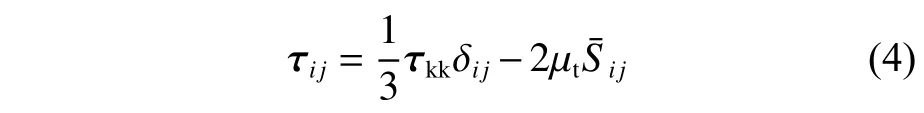
式中：τkk为亚格子应力中的各向同性成分；=µt为亚格子尺度的湍动黏度，文献[18]推荐使用式（5）进行计算。

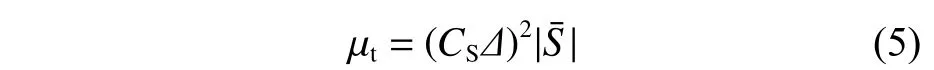
1.2 随机速度扰动算法

频谱合成法被广泛应用于随机速度扰动的产生。本文利用频谱合成法对入口速度施加扰动，并与湍流生成栅格（详见图1，图中U0为入口平均速度，C为格栅尺寸）相结合，以产生具有时间脉动和空间相干结构的湍流。脉动速度分量从通过傅里叶谐波求和合成的无散度矢量场中提取，瞬时速度由傅里叶级数定义[19-20]：

图1 计算域和边界条件Fig.1 Computational domain and boundary conditions

式中：vi为速度入口边界的速度；l为湍流尺度；τ为湍流时间尺度；为波数；ωn为 频率；与分别为控制波数和频率分量的系数，满足正态分布。

1.3 计算模型

本文的研究对象为某11叶前置定子、9叶转子泵喷推进器，其几何参数如表1所示，建立的计算域如图1所示，并对其开展非定常力宽带谱特性数值仿真。

表1 泵喷推进器的几何参数Table 1 Parameters of pump-jet

模型中，湍流生成栅格的尺寸为164 mm，为了确保到达推进器的湍流能充分发展，在计算时，将泵喷推进器设置于湍流生成栅格下游20C处。设入口位于湍流生成栅格上游4C处，出口位于推进器下游10C处，用以消除数值边界对转子周围流量波动的衰减作用。计算时，将推进器的转速设置为900 r/min，设平均入口速度U0=3.051 m/s，对应的进速系数为0.93。首先，采用SSTk-ω湍流模型进行定常计算，待结果收敛之后再以其为初始流场，采用LES模型进行非定常计算。计算时，压力速度耦合采用SIMPLEC 算法，空间离散格式均采用二阶迎风格式。

在湍流生成栅格的涡旋穿过泵喷推进器之后，从1.08 s（20C/U0）开始记录脉动数据。为了保证足够的时间分辨率，一圈之内采样360个时间点，计算得到的最高频率为2 700 Hz，包含计算工况前4阶的转子叶频。共计算6.42 s（对应于泵喷推进器中转子旋转96圈的时间），以便在频域中获得足够的分辨率。当单独计算转子时，将泵喷前置定子和导管去除，计算方法不变。

1.4 网格划分

模型网格划分在ICEM软件中进行，采用全结构网格对计算模型进行离散，并将边界层进行加密处理。图2（a）所示为整个外部计算域网格。由于计算模型需要模拟实际湍流的作用，因此入口段的网格不能从疏到密过渡，在整个计算域流向方向均需划分相对较密的网格，以防止入流湍流耗散。对于栅格区域，采用Y形网格拓扑栅格交叉部分的计算域，采用O形网格生成栅格外围的边界层，结果如图2（b）所示。针对定子区域，首先对单流道计算域进行划分，为了充分捕捉定子尾流，单流道计算域根据定子预旋方向进行布置，随后旋转生成全流道网格。对导管和定子壁面附近的网格进行加密，设置导管和壁面边界层第1层网格的厚度为0.01 mm，最终的网格如图2（c）所示。转子桨叶周围采用H型网格进行布置以生成边界层，设第1层网格的高度为0.005 mm。采取该划分方式，得到网格正交性最小值为0.61，最小扭曲角度大于18°，满足结构网格的计算要求，如图2（d）所示。上述网格划分的密度参考文献[11]中对十叶螺旋桨非定常力计算网格验证时的经验，最终共计生成网格2 800万，其中转子区域800万。

图2 泵喷推进器计算网格Fig.2 Grid of pump-jet

2 结果与分析

2.1 宽带谱处理方法

计算完成之后，取非定常计算1.8～6.42 s内的脉动数据进行分析。首先，将原始的非定常时域结果分成具有1/3重叠的区间，应用汉宁窗，通过快速傅里叶变换（fast Fourier transform，FFT）将每个区间转换到频域，然后，再将所有区间的力谱进行平均，并根据式（9）将幅值T(N)转换到分贝T(dB)：

为了获得连续谱，滤去原始谱中幅值较低的频点，以避免低估实际的脉动幅值，本文采用两步法提取连续宽带频谱。首先，根据平均后的推力谱计算原始频谱的上包络，获得波动幅值局部最大值；然后，根据式（10）使用相邻平均加权法对极大值进行处理。该算法可以正确反映非定常力的脉动幅值，对包络曲线进行平滑处理，消除随机分量。

式中：fi，gi分别为第i个输入和输出数据点；N为窗口中的点数；wj为二次加权因子。

2.2 泵喷推进器力谱特性

图3（a）所示为泵喷推进器转子侧向力、垂向力和推力的宽带力谱。由图可见，平均后的原始推力频谱在整个频率范围内显示出明显的宽带特性，并且在叶频及其倍频处均出现了离散分量。由于大多数频谱峰值在频率和幅值上都比较相近，因此力谱的上包络在视觉上呈宽带特性。根据两步法最终提取的非定常推力谱如图3（a）所示，从中可以清楚地看到各阶叶频中心附近的“驼峰”，其中1～3阶叶频处的特别明显。由于入流具有湍流特性，当泵喷推进器的转子转过一个相邻桨叶的夹角时，桨盘面处的瞬间速度场已经不同于初始状态，使得流场的周期性重复减弱。在1阶叶频及其倍频处出现了 “驼峰”，也即低频宽带谱，该宽带谱反映了入流的时间非定常性。从图3（a）中还可见，非定常力宽带谱的能量主要集中在低频区域，具有向高频衰减的趋势。在宽带力激励下，在低频范围内会激励起螺旋桨固有频率、螺旋桨−轴系系统固有频率的随机振动响应。由推进器转子三向力的频谱对比可见，侧向力和垂向力同样在叶频及其倍频处出现了“驼峰”，并且侧向力谱和垂向力谱的幅值比较接近，均比推力谱的幅值低。

图3（b）所示为采用两步法最终提取的泵喷推进器导管、定子和转子的三向非定常力谱。由图可见，导管和定子在叶频以及其倍频处出现了“驼峰”，但没有转子的明显。对导管来说，其侧向力和垂向力的幅值相比推力大，这是因为转子的诱导涡主要作用在导管的侧向和垂向上。定子的三向非定常力谱十分接近，均具有向高频衰减的趋势。

图3 泵喷推进器非定常力谱Fig.3 Unsteady force spectrum for pump-jet

图4（a） 所示为泵喷推进器中单个叶片的原始推力谱、侧向力谱及垂向力谱。从图中可见，单个叶片的脉动推力谱是以定子叶频（165 Hz）为主要特征峰值，未出现宽带特性，其原因是单个叶片工作在前置定子提供的11阶空间非均匀流场后。侧向力谱和垂向力谱是以轴频（15 Hz）为主要特征峰值，同时出现了定子个数±1的倍轴频（150，180 Hz）。但无论是推力谱还是侧向力谱，除了在特征频率处出现峰值外，并未在叶频及其倍频处出现“驼峰”，并且整个力谱向高频呈现出衰减的趋势。

图4 泵喷推进器单个叶片力谱(原始力谱)及特征峰值变化Fig.4 Unsteady force spectrum (original spectrum) for single blade and the variation of characteristic peaks for pump-jet

针对泵喷推进器的转子，将同一个转子中不同叶片的脉动力时域结果叠加，以获得不同叶片数下的非定常力谱，从而说明力谱“驼峰”的产生趋势。图4（b）～图4（d）为不同叶片数量叠加后三向力谱特征峰值的变化趋势，为便于比较，将原始幅值同时变为正值进行了显示。图4（b）和图4（c）给出了15，150，180 Hz处的侧向力谱与垂向力谱，从中可以看出，随着叶片数量的，15 Hz 和150 Hz处的幅值出现了先增加后减小的趋势，180 Hz处的幅值出现了周期性的变化，但均在9个叶片时达到最低。图4（d）给出了推力谱在叶频（135 Hz）和定子叶频（165 Hz）处的幅值变化。对于脉动推力谱，其叶频处的幅值是随叶片数量的增加而逐渐递增，除9个叶片外，均比同叶片数量下定子叶频的幅值低，且在9个叶片时达到最大。而定子叶频处的幅值出现了周期性先增加后减小的趋势，在叶片数量为9时急剧降低。此时，不同叶片之间的脉动力相位相互抵消，导致定子叶频处的幅值急剧降低，转子叶频处的峰值达到最大值。

针对图4中的原始力谱，采用两步法进行处理，并将上文中获得的不同叶片数下的推力、侧向力和垂向力非定常力谱予以对比，其结果如图5所示。由于对原始力谱中的包络采用相邻加权平均算法进行了平滑处理，故在宽带力谱中看不到特征线谱，但这不影响观察叶频及其倍频处“驼峰”的变化趋势。可见对单个叶片来说，侧向力谱、垂向力谱和推力谱在叶频及其倍频处几乎没有“驼峰”，在整个频段内呈现连续衰减的趋势。随着叠加叶片数量的增加，三向力谱在叶频及其倍频处的“驼峰”更加明显。由图5（c）可见，推力谱的低频曲线斜率随着叶片数量的增加并非单调增加，这表明低频处的衰减速度与叶片数量不是单调变化的关系。

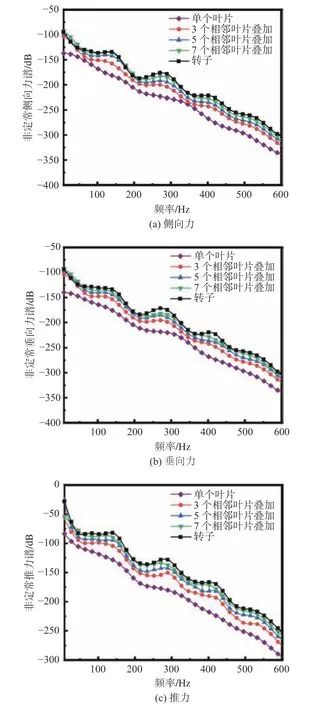
图5 泵喷推进器不同叶片数量时的非定常力谱Fig.5 Unsteady force spectrum of pump-jet under different blade numbers

2.3 螺旋桨力谱特性分析和比较

为了说明泵喷推进器与螺旋桨非定常力谱的区别，本文将前置定子和导管去除，仅保留转子（相当于螺旋桨）进行了非定常计算，计算所采用的方法和数据处理方式与前文相同。图6（a）所示为螺旋桨的三向力谱。由图可见，对于单独的转子，其力谱的幅值比泵喷推进器的低，但其叶频附近的“驼峰”更加“挺拔”，且仅在1阶叶频和2阶叶频处出现了明显的“驼峰”。同样，其脉动推力谱比垂向力谱和侧向力谱都要大，这与泵喷推进器的力谱特征相同。

将螺旋桨不同叶片数的脉动力时域结果叠加，获得不同叶片数下螺旋桨的推力非定常力谱如图6（b）所示。由图可见，随着叶片数量的增加，其在叶频及其倍频处产生的“驼峰”更加明显。同时，低频段曲线的斜率为单调增加，这说明其衰减速度是单调递增的，并且当9个叶片同时叠加（即整个螺旋桨）时，衰减速度会急剧增加，并在叶频“驼峰”右侧形成一个明显的波谷。

图6 螺旋桨非定常力谱Fig.6 Unsteady force spectrum of propeller

图7（a）所示为螺旋桨单个叶片的原始非定常力谱。从中可以发现，螺旋桨单个叶片推力谱的特征峰值为2倍、4倍和6倍的轴频，而侧向力和垂向力谱的峰值则主要为1倍、3倍、5倍和7倍的轴频。由此可见，单个螺旋桨叶片侧向力和推力的主要特征峰值均为轴频倍数，且间隔出现。由于螺旋桨没有前置定子，故在定子叶频处未产生特征峰值。经与泵喷推进器侧向力和推力峰值进行比较可以发现，其侧向力谱的主要峰值均是与推力谱主要峰值相邻的倍轴频。取出螺旋桨单个叶片非定常力谱特征峰值随叶片数量的变化图如图7（b）～ 图7（d）所示，为便于比较，同样将其转换到了正值。由图可见，除15 Hz轴频外，其余特征峰值均为周期性的变化，且所有幅值均在叶片数量为9时达到最小值。

图7 螺旋桨单个叶片力谱(原始力谱)及特征峰值变化Fig.7 Unsteady force spectrum (original spectrum) for single blade of propeller and the variation of characteristic peaks for original spectrum

3 泵喷推进器和螺旋桨流场特性对比分析及脉动力时间历程分析

影响力谱的因素包括外部湍流环境因素和螺旋桨运转工况条件。其中外部湍流环境因素主要包括湍流积分尺度和湍流强度，螺旋桨运转工况则包括入流速度和旋转速度[21]。本文中螺旋桨与泵喷推进器的入口边界湍流强度和采用的栅格大小均相同，大小相同的栅格保证了由栅格大小产生的涡旋大小相同，且设置的入口来流速度和转速也相同，因此，力谱的差异需要从螺旋桨和泵喷推进器附近的流场来进行分析。

前置定子泵喷推进器的转子工作在前置定子的复杂尾流中，流体经过前置定子后会形成空间非均匀的流场，给转子入流提供预旋，增加周向诱导的速度，从而产生更大的推力。转子和定子之间的动静干涉、导管边界层流动、导管内壁面和转子之间的间隙泄漏涡，都使得泵喷推进器的转子非定常力变得复杂。图8所示为Q值（即速度梯度张量第二不变量）为30 000时的涡量等值面，其中的压力显示为云图。由图可见，泵喷推进器转子因工作在定子尾涡和导管内壁面的湍流边界层之内，故其涡系非常复杂。入口栅格产生的大的涡旋经过定子后会形成小的涡旋，从而减小湍流积分尺度的大小，而同时导管内壁面湍流边界层会增加泵喷推进器转子入流盘面的湍流强度。湍流强度的增加将提升泵喷推进器非定常力谱的整体幅值。湍流积分尺度越大，两点之间湍流速度的相关性越大，对湍流速度周期性的影响也就越大，湍流积分尺度的增大会导致激振力谱的整体减小[22]。螺旋桨直接工作在入口栅格产生的尾涡中，相比泵喷推进器，其湍流积分尺度更大，在叶频处的“驼峰”更加明显，并且在高频处力谱的衰减也更快，在三阶叶频处几乎没有“驼峰”。

图8 Q=30 000时螺旋桨和泵喷推进器流场中的涡量对比Fig.8 Comparison of vorticity in flow field of propeller and pump-jet at Q=30 000

为了详细说明泵喷推进器与螺旋桨入流速度的区别，在入流段创建了如图9（a）所示的4个截面，其中截面S1位于定子入流前方，截面S2～S4位于定、转子之间。图9（b）所示为不同截面处轴向速度Ux和入口平均速度U0的比值云图。由速度大小的对比可以看出，螺旋桨入流界面的轴向速度相比泵喷推进器要低，这相当于相比泵喷推进器，螺旋桨的旋转速度更大，此时由转速导致的周期性影响也就越发明显，进而导致峰值越明显[21]。从云图中速度的分布规律可以看出，螺旋桨截面S1～S3处的轴向速度分布基本没有规律，高速区和低速区是随机分布的，而受螺旋桨旋转的影响，在截面S4处，速度的分布开始出现规律，该规律与螺旋桨的叶片数相对应。泵喷推进器受到前置定子的影响，在截面S1～S4处其速度云图的分布均出现了明显的规律，并且在截面S2，S3处已形成明显的11阶流场。因此，泵喷推进器中定子的使用使得泵喷推进器在原始时间非定常的入流条件中叠加了空间非均匀流场的特性，增加了泵喷推进器非定常力中周期分量（定子叶频）的成分，导致在叶频处速度的周期性被削弱，最终在叶频及其倍频附近产生了更多频率和幅值接近的峰值，进而使得非定常力谱的“驼峰”变得更宽。

图9 泵喷推进器和螺旋桨不同截面的速度分布Fig.9 Velocity distribution in different sections for pump-jet and propeller

由于转子叶频处的周期性不明显，下面将从时间历程的角度说明泵喷推进器力谱中定子叶频的产生机理。图10所示为3个典型时刻的瞬态流场和不同叶片脉动推力的时域历程。由于单个叶片与合力数据间的大小差别较大，为在同一坐标下显示观察到的趋势，将叶片合力向下平移30 N进行了比较。由图10（d）可见，叶片1在一个周期内(6.000 0～6.066 7 s)具有11个峰值，且相邻两个峰值之间的时间间隔为6.060 6 ms，对应的转子转过32.73°所需时间与定子数对应。这说明单个叶片在频域内的主要峰值为定子叶频，这与图4所示结论相同。但叶片1的时间历程曲线在平移7.407 3 ms（对应的叶片旋转40°）后无法与叶片2的重合，这也反应了入流条件的时间非定常特性，当叶片经过相同的位置时，叶片的入流攻角发生了变化，不再具有严格的周期性。

图10（a）～图10（c）所示为流场中0.8R（R为转子半径）截面处3个不同时刻的轴向速度分布云图。从中可以看出，由于存在前置定子，流场中的瞬态速度场具有明显的不均匀性。图中，T1=6.006 1 s，Δt1为转子转过16.36°所需的时间3.030 3 ms。在T1时刻，叶片1刚好位于定子尾流形成的低速区域，之后有向高速区域运动的趋势，因此叶片1的推力产生了局部最大值。此时，叶片2正在转入定子尾流的低速区域，攻角变大，因而推力也有增加的趋势。两者叠加之后，其合力在T1时刻产生了极大值。随着转子的旋转以及入流湍流的作用，在T1+Δt1时刻，叶片1处于2个定子之间，开始进入高速区域，此时叶片的负载最低。同时，叶片2驶出定子尾流低速区，转向高速区，负载有降低的趋势。因此在T1+Δt1时刻，2个叶片叠加之后的合力产生了极小值。在T1+2Δt1时刻，叶片1进入定子尾流低速区域，叶片2从高速区域向低速区域移动，2个叶片的负载均比较大，其合力又产生了极大值。

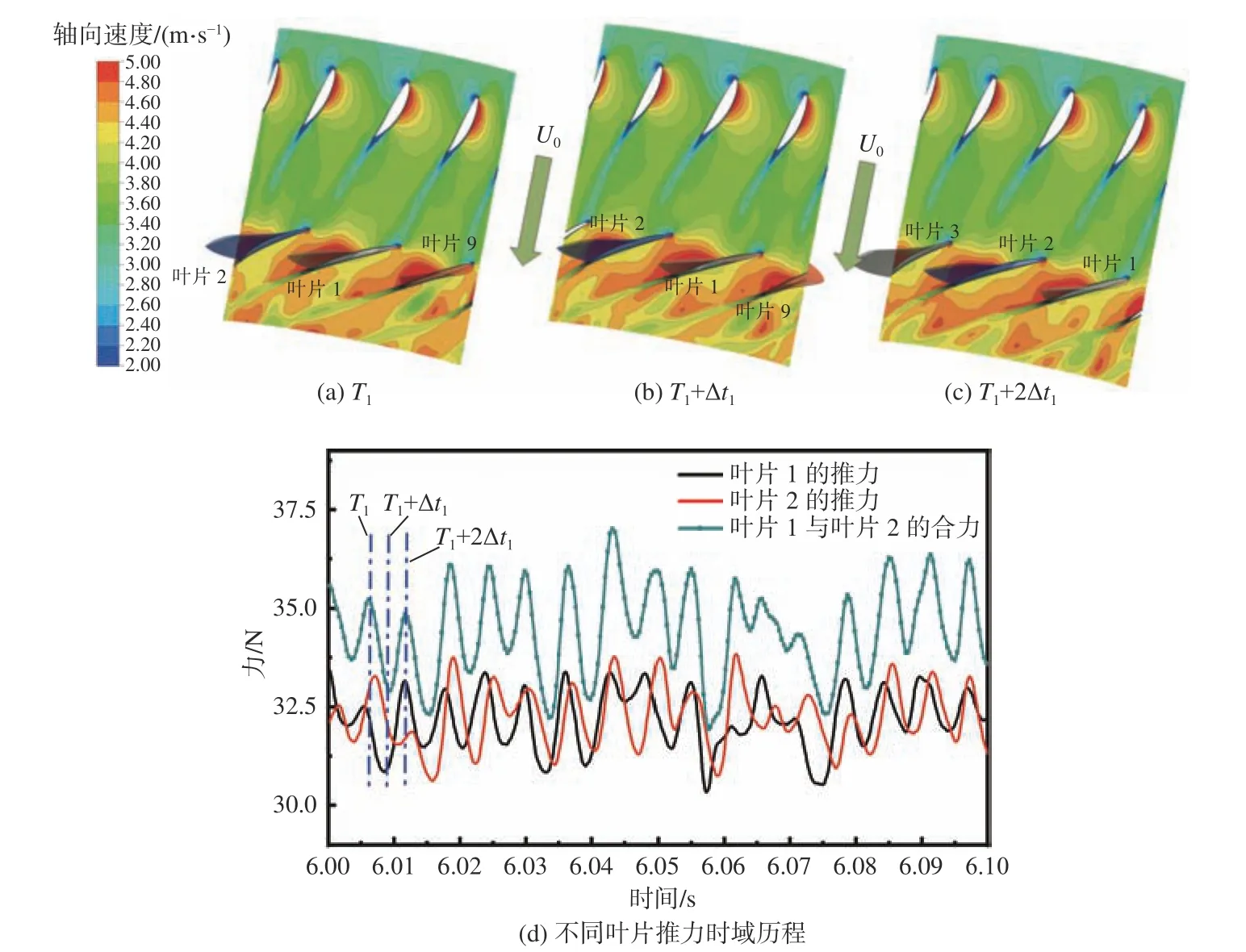
图10 3个典型时刻泵喷推进器的瞬态流场和不同叶片推力的时域历程Fig.10 Instantaneous flow field at three moments and time-domain history of different blade thrust

由上面的讨论可知，每个叶片推力的单峰值（T1时刻和T1+2Δt1时刻）有助于其合推力双峰值的产生，此时的时间间隔为2Δt1，对应于1倍定子叶频。由于入流湍流的作用，每个叶片从T1时刻开始经过2Δt1时刻时，流场中具有不同的低速区域，因此叶片1在T1与T1+2Δt1时刻的推力并不相同。

4 结 论

本文针对湍流入流条件下的11叶前置定子、9叶转子泵喷推进器的非定常力谱进行了计算分析。通过湍流生成栅格和随机速度扰动的方法，实现了入流湍流，并采用LES计算了非定常力谱。对原始力谱做包络和相邻加权平均处理，获得了该泵喷推进器的非定常力宽带谱。通过对该泵喷推进器的力谱进行分析，得到以下主要结论：

1） 在湍流作用下，泵喷推进器的非定常力谱会在叶频及其倍频附近出现频率和幅值接近的峰，进而使泵喷推进器力谱在叶频及其倍频附近产生“驼峰”；其中，转子推力谱的幅值最大，侧向力谱和垂向力谱的比较接近；导管的侧向力谱和垂向力谱比较接近，均小于推力谱；定子的三向力谱均比较接近。

2） 与具有相同转子几何的螺旋桨非定常力谱不同，由于前置定子形成了空间非均匀流场，因此在泵喷推进器单个叶片的非定常力宽带谱中，推力谱会在定子叶频、侧向力谱会在叶频的相邻倍轴频处产生特征线谱；在同一转子中，随着叠加叶片数量的增多，力谱中叶频及其倍频处的“驼峰”将变得更加明显；特征线谱的峰值幅值呈周期性变化，当叠加个数为整个转子时，特征线谱的幅值达到最低，整个力谱呈现出宽带特性。

3） 泵喷推进器的转子工作在定子尾流和导管内壁面湍流边界层内，增加了转子区域的湍流强度，同时减小了湍流积分尺度，由此导致泵喷推进器转子的非定常力宽带谱相比具有相同转子的螺旋桨的宽带谱整体幅值要高，产生的“驼峰”更宽。