船体伴流对直翼推进器水动力性能的影响
黄璐,陈奕宏,曾柯,刘竹青
中国船舶科学研究中心,江苏 无锡 214082
0 引 言
直翼推进器又名摆线推进器,是一种船用特种推进器,可在任何方向产生从0至最大值的推进力和转向力。该推进器通过从船舶底部伸出并围绕垂直轴做往复式摆动的桨叶产生推力,桨叶安装在与船舶底部齐平的旋转箱体上[1]。借助连杆机构,每片桨叶围绕其自身的轴进行局部往复式摆动,同时,也围绕与所有桨叶共有的垂直轴进行摆动,该双重摆动产生的推力会在旋转箱体上实现叠加。对常规螺旋桨而言,推力的方向与旋转轴一致,而直翼推进器的推力与旋转轴相互垂直,因此直翼推进器所产生的推力无首选方向,允许推力的大小和方向无级可调。整个系统的安装因只有桨叶伸出船体外,因此避免了其他部件,如舵、桨轴等附体阻力的影响[2]。
早期,许多学者应用各种理论方法针对直翼推进器的水动力性能预报开展了研究,根据数学模型的理论依据,大致可以分为以下4类:1)基于升力线原理的直翼推进器水动力性能计算方法;2)基于动量定理的直翼推进器水动力性能计算方法;3)基于漩涡理论的直翼推进器水动力性能计算方法;4)基于黏流CFD的直翼推进器水动力性能数值计算方法[3]。由于直翼推进器桨叶多重运动复杂,目前国内外的研究多集中在基于桨叶时均受力性能分析上[4]。同时,直翼推进器的回转轴垂直于船体安装在船后,工作时,船尾流体的加速会导致尾部压力分布改变,从而影响船体阻力和船舶尾部边界层厚度以及边界层内的速度分布,而边界层的变化会影响到推进器的进流条件,进而有可能会引起空泡[5]、噪声[6]等相关问题。因此,有必要开展直翼推进器的非定常水动力性能研究和船体伴流对直翼推进器水动力性能影响研究。
本文拟通过分析直翼推进器的工作原理,推导出叶片多重运动规律公式,然后基于RANS方程和k−ε湍流模型计算直翼推进器的敞水性能,并与试验值对比,以验证直翼推进器水动力性能预报方法的准确性,同时,在综合考虑船体伴流影响的基础上,通过对船艉关键区域的网格加密策略,研究船体伴流对直翼推进器非定常水动力性能的影响。
1 直翼推进器的工作原理及水动力表达
1.1 直翼推进器的工作原理
直翼推进器的叶片围绕中心轴沿圆周运动,同时绕自身轴进行往复式运动。如图1所示,叶片在运动过程中由内部连杆机构控制以使其弦线始终与叶片轴心至某一点N的连线垂直,称该点N为偏心点,控制点N到圆心O的距离称为偏心距ON,偏心距ON与叶片公转半径R的比值称为偏心率e(e=ON/R),推导出叶片摆角的运动规律为:
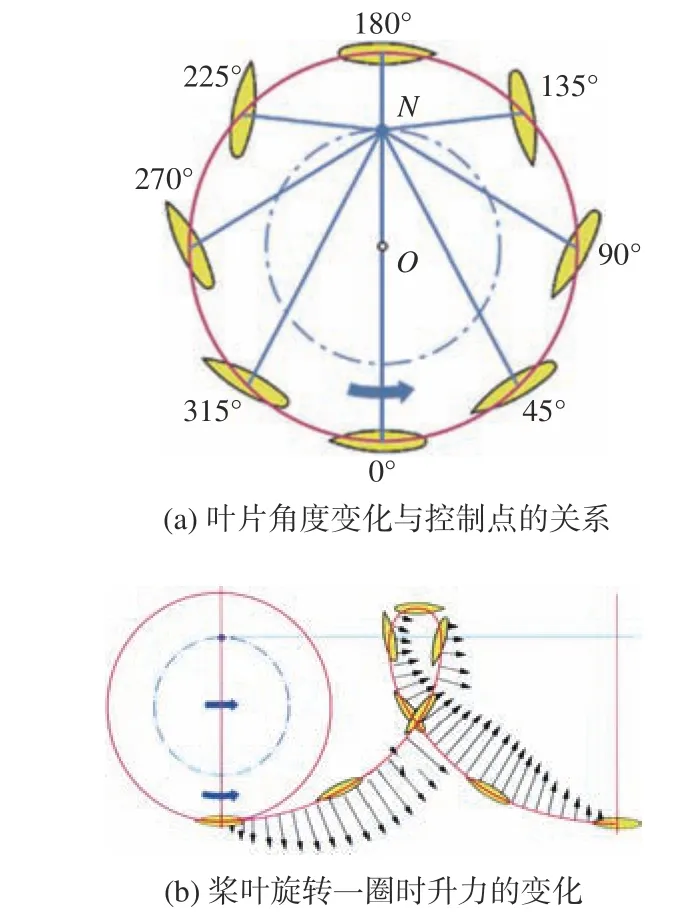
图1 桨叶摆线上的升力分布Fig.1 Lift force distribution on the blade

式中:ωc为 叶片绕自身轴线摆角的角速度;ω为桨叶围绕中心轴旋转的旋转角速度;θ为桨叶绕中心轴的转角。
1.2 直翼推进器的水动力表达
桨叶转动时,除0°和180°位置外,桨叶弦线始终与来流方向保持正攻角,因而产生升力。升力在前进方向的分力即为推力,在垂直于前进方向的分力即为侧推力,桨叶升力和阻力对转盘中心的合力矩即为转矩。直翼推进器的主推力T,侧推力S和转矩Q分别为各叶片旋转一周的平均主推力、平均侧推力和平均转矩的叠加[7],为了表征直翼推进器的水动力特征,可以通过无因次系数来表示。在无因次表达中,与螺旋桨的常数因子不同,直翼推进器将桨叶长度L结合到了相应的推力和扭矩系数中,主推力系数KT、侧推力系数KS、转矩系数KQ、效率η和进速系数J的表达式分别为:
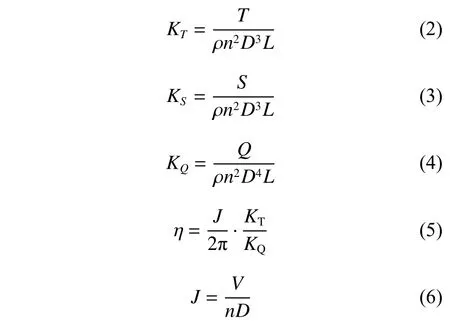
式中:ρ为流体密度;n为 直翼推进器转速;D为直翼推进器回转直径;V为来流速度。
2 直翼推进器水动力数值模拟方法
2.1 控制方程
本文将模拟直翼推进器周围的黏性流场,采用非定常RANS求解器STAR-CCM+ 12.0进行求解。为了求解RANS方程,每一个求解变量φ(包括速度、压力等参量)在瞬时的N-S方程中都被分解成平均值和脉动值φ′。
平均物理量的质量和动量输运方程可以表示为:

由于动量方程中的雷诺应力张量项使控制方程不再封闭,因此需要引入湍流模型进行求解。本文选取理论上发展较为完善,在工程上应用较为广泛的k−ε湍流模型来封闭RANS方程[8]。
分离迭代求解方法是基于SIMPLE算法,采用二阶迎风格式离散求解RANS方程中的对流项,然后利用二阶欧拉隐式格式进行时间积分。近壁面边界层流动采用壁面函数进行求解。时间步长根据每个时间步公转1°进行设置,在每个时间步内迭代计算15次。
2.2 网格模型
直翼推进器叶片存在公转和自转的双重旋转,为了实现直翼推进器的工作,采用双重滑移网格方法,如图2所示。首先,在各叶片附近以叶片转轴为圆心设置小圆柱域,直径0.25D,高0.6D,小圆柱体和叶片一起实现自主摆动。其次,以整个直翼推进器的中心为圆心设置大圆旋转域,直径0.8D,高0.8D,包裹桨叶的小圆柱域绕大圆柱域中心轴旋转以实现叶片的公转。

图2 直翼推进器滑移网格Fig.2 Sliding meshes of cycloidal propeller
3 直翼推进器水动力数值预报
3.1 计算对象及计算网格
美国海军研究与发展中心的Ficken等[9]于1969年发表的2 938号报告是目前研究直翼推进器性能资料中最为全面的试验报告,该报告详细阐述了直翼推进器的偏心率e= 0.4~0.9的试验结果。本文参考了2938号试验报告中的几何叶片,计算的几何模型尺寸如表1所示(表中,C为弦长),计算模型的几何建模如图3所示。

表1 直翼推进器计算模型几何尺寸Table 1 Geometric dimensions of calculation model of cycloidal propeller

图3 直翼推进器几何模型Fig.3 Geometric model of cycloidal propeller
计算域为长方形,其中入口距离直翼推进器前方4D,出口距离直翼推进器12D,侧面距离直翼推进器4D,底面远场距离直翼推进器4D。为了验证不同网格量对计算的影响,保证网格拓扑形式一致,分别针对方案1(229万网格量)和方案2(508万网格量)开展了研究。其中方案1的基准网格尺度BS为0.08D,方案2的基准网格尺度为0.06D,桨叶表面网格尺度为6.25%BS,包裹叶片的小圆柱域最大尺度为12.5%BS,包裹直翼推进器的大圆柱尺度为25%BS,边界层生成6层网格,增长比例为1.2,边界层第1层网格高度依据Y+值在30~100之间进行确定。通过计算发现,两套网格的计算误差分别为3.71%和3.57%,综合考虑其计算效率和计算精度,优选方案1作为网格划分方案。
将入口边界处设置为速度入口条件,计算域长方体顶面、侧面设置为壁面条件,出口边界定义为压力出口条件;大圆柱域外壁面设为交界面;大圆柱域与小圆柱域之间的相交面设为交界面,叶片设为无滑移物面条件。
3.2 水动力系数与试验的对比验证
图4所示为偏心率e=0.5,0.7,0.9时直翼推进器的推力系数和转矩系数随进速系数的变化曲线。由图中可以看出,数值模拟结果与试验结果基本吻合,主推力系数误差约为5%,转矩系数误差约为7%;在一定偏心率下,推力系数和转矩系数随进速系数的增大而减小;在同一进速系数下,随着偏心率的增大,推力系数和转矩系数随之增大,且推进器产生正推力的进速系数范围也相应增大。
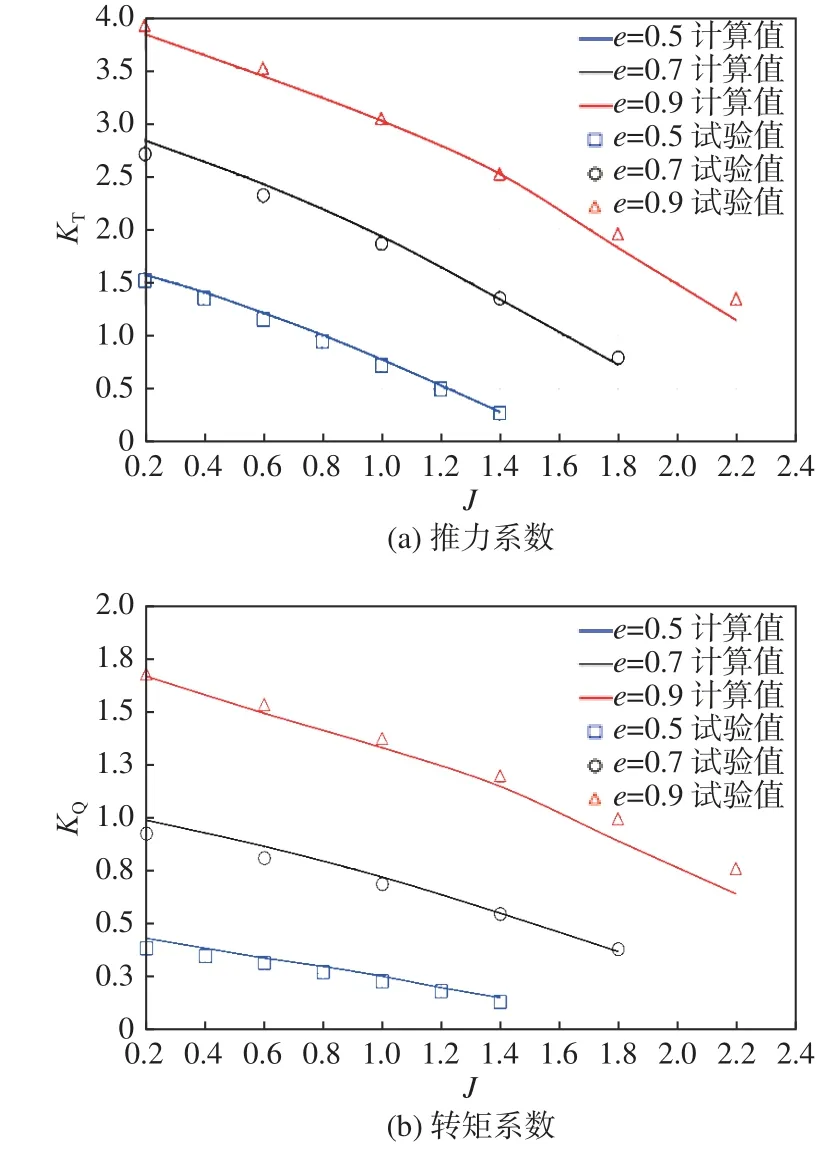
图4 直翼推进器敞水性能Fig.4 Open water performance of cycloidal propeller
3.3 单叶片瞬时载荷变化规律分析
图5所示为不同进速系数下桨叶(e=0.7)旋转一周的主推力变化曲线。从中可以看到,随着进速系数的减小,单叶片载荷波动幅值增大,瞬时载荷峰值出现在约300°桨叶转角处,此时桨叶的有效攻角最大;在桨叶转角为0°和180°时,主推力为0,此时桨叶摆角为负,桨叶有效攻角为0。图6所示为单叶片1在一个周期内的压力变化图。从中可以看到,当桨叶转角为300°时,桨叶压力面和吸力面的压差最大,故叶片瞬时载荷出现峰值,而在桨叶转角为0°和180°时,桨叶压力面和吸力面的压差最小,此时叶片的主推力为0。
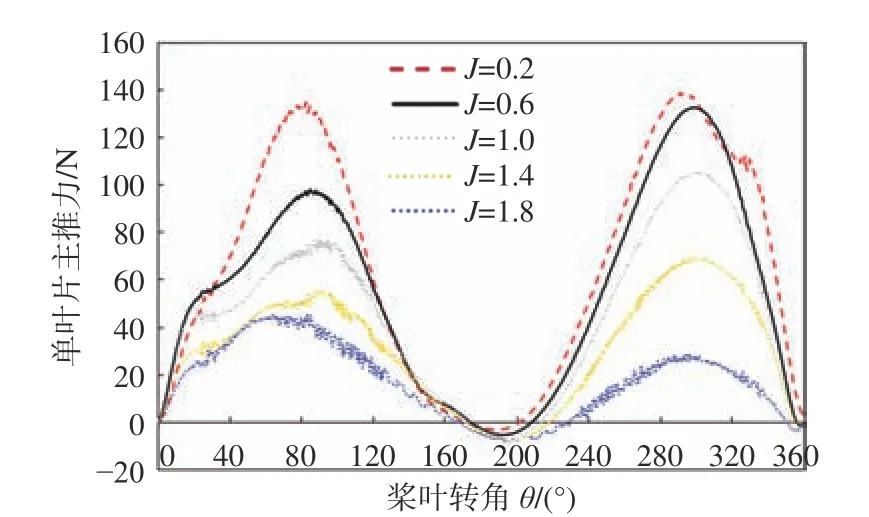
图5 不同进速系数下单叶片1的瞬时载荷变化规律(e=0.7)Fig.5 Variation of instantaneous load of single blade 1 at different advance coefficients (e=0.7)
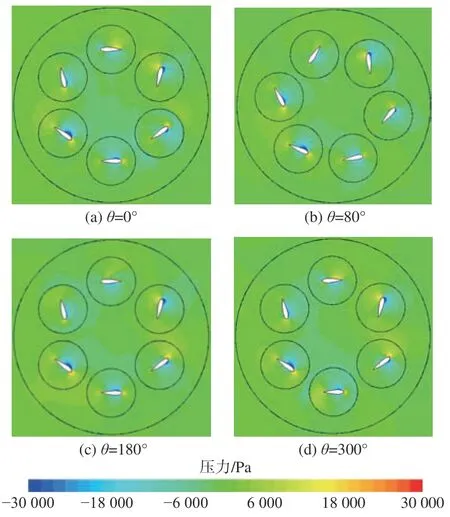
图6 单叶片1的压力分布变化Fig.6 Variation of pressure distribution of single blade 1
图7所示为各桨叶旋转一周的主推力变化曲线图。从中可以看到,各叶片上的载荷变化情况基本相同,由于叶片间存在位置角差,故叶片载荷变化也存在相位差[10]。前半圈叶片的主推力峰值低于后半圈,这是因为来流经前半圈叶片的诱导作用后速度增加了,经过2次加速后获得了较高的推力。

图7 单叶片的瞬时载荷变化规律Fig.7 Variation of instantaneous load of single blades
3.4 整桨瞬时载荷变化规律分析
直翼推进器在实际运行过程中所受的瞬时载荷在时均值附近是不断波动的,其主要原因是单叶片在旋转一周的过程中因摆角变化会引起攻角的改变,进而受力也会随之变化,各叶片的受力叠加后就体现为整个直翼推进器的瞬时载荷波动。图8所示为偏心率e=0.7工况下一个回转周期内的整桨主推力和转矩变化曲线。从中可以看出,主推力和转矩随桨叶转角呈周期性波动,其周期为推进器回转周期的1/6,且随着进速系数的减小,主推力和转矩的波动幅值增大。
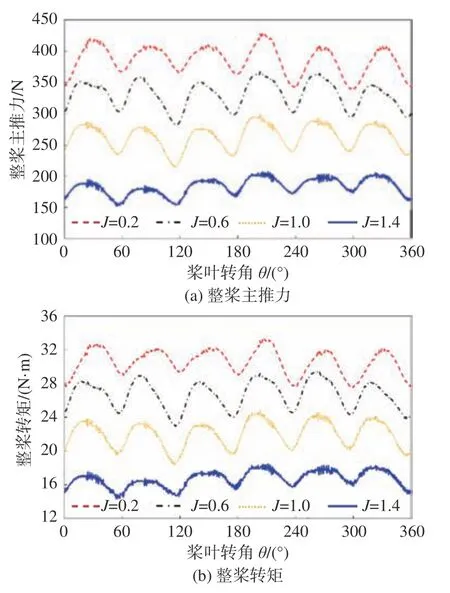
图8 整桨瞬时载荷变化(e=0.7)Fig.8 Variation of instantaneous load of cycloidal propeller(e=0.7)
4 船后直翼推进器的水动力性能
4.1 船后直翼推进器水动力载荷预报方法
为研究船体伴流对直翼推进器水动力性能的影响,建立船后直翼推进器水动力载荷预报方法。考虑在长6.08 m、吃水为0.28 m的水面船舶尾部对称布置2个直翼推进器,直翼推进器采用3.1节的研究对象。
计算域为长方形,其中入口距离船艏前方1.5Lpp(Lpp为船体垂线间长),出口距离船艉2.5Lpp,侧面距离船舯1.8Lpp,底面远场距离船舯1.5Lpp。为了进行网格收敛性分析,分别针对376万、686万、1 540万网格量进行了计算,这3套网格的基准网格尺度分别为0.438D,0.35D和0.263D;船体表面最大网格尺度为25%BS,桨叶表面网格尺度为1.562%BS,包裹叶片的小圆柱最大尺度为3.125%BS,包裹直翼推进器的大圆柱域最大网格尺度为6.25%BS,边界层生成6层网格,增长比例为1.2,边界层第1层网格的高度依据Y+值在30~100之间确定。计算表明,当网格数为686万时,数值预报可达到较好的精度且具有较高的计算效率。图9所示为船体和直翼推进器的计算网格。
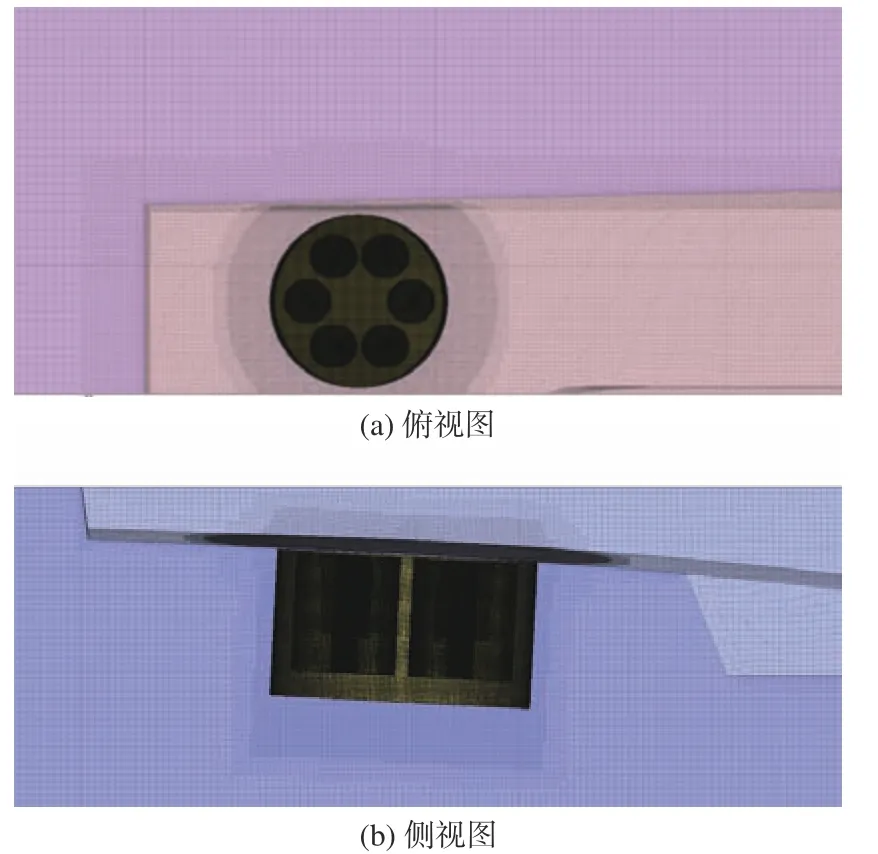
图9 船体和直翼推进器网格图Fig.9 Meshes of ship and cycloidal propeller
4.2 船后直翼推进器水动力性能分析
考虑船体伴流的影响,模拟直翼推进器船后的水动力,计算在偏心率e=0.7工况下,伴流条件和敞水条件下的主推力系数、转矩系数及侧向力系数对比,如图10所示。由图可以看出,船体伴流对直翼推进器主推力系数和扭矩系数的影响并不大,但对侧向力具有明显的影响;在偏心率e=0.7工况下,考虑船体伴流影响后,侧向力明显减小,其原因可能是船艉对称优化布置的直翼推进器使侧向力得到了改善。
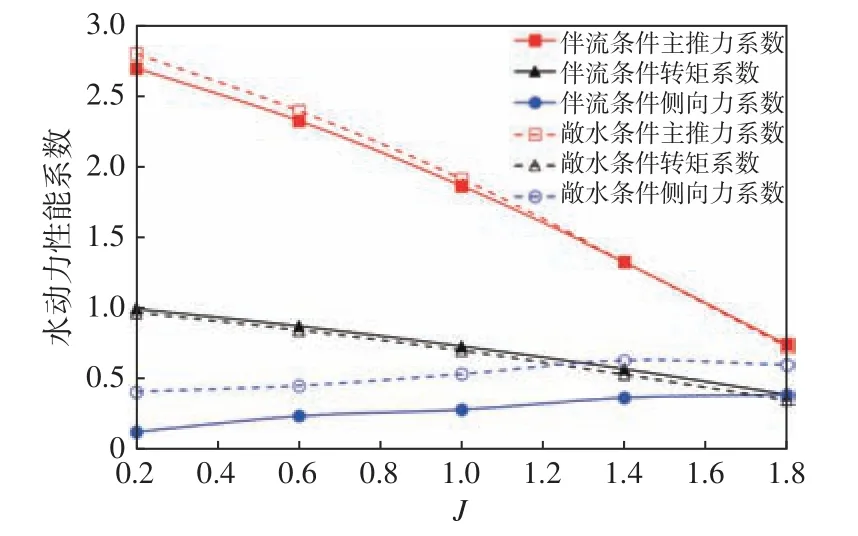
图10 船体伴流对直翼推进器水动力性性能影响(e=0.7)Fig.10 Influence of ship wake on hydrodynamic performance of cycloidal propeller (e=0.7)
4.3 侧向力瞬时载荷变化规律分析
图11所示为伴流场下直翼推进器整桨和单叶片侧向力随桨叶转角的变化曲线。从中可以看出,伴流条件与敞水条件下的载荷变化趋势基本一致,但由于船体伴流的影响,单叶片的侧向力峰值显著下降,所以宏观上呈现侧向力变小的现象。在敞水条件下,侧向力在一个周期内波动变化,整桨多叶片侧推力的叠加会使船体产生横摇,在船后布置时,通过安装合适位置的旋向相反推进器来抵消侧推力,可使侧向力减小。
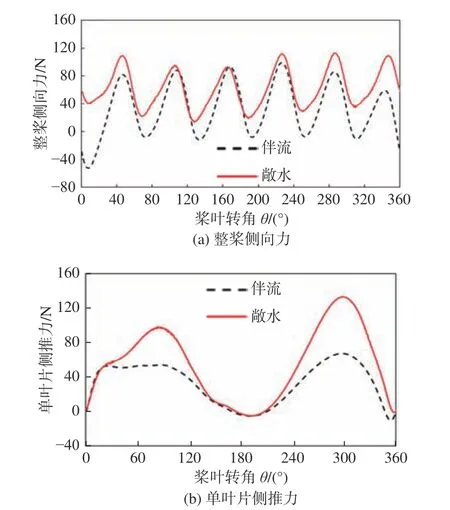
图11 整桨和单叶片瞬时载荷变化规律分析(侧向力)Fig.11 Variation of instantaneous load of cycloidal propeller and signal blade (lateral force)
4.4 带直翼推进器的船后尾涡结构分析
采用不同的进速系数分析船后直翼推进器尾涡的变化特征,进速系数的取值分别为J=0.2(0.452 7 m/s),J=1.0(2.286 m/s)和J=1.8(4.114 8 m/s)。图12给出了偏心率e=0.7工况下不同进速系数时船后直翼推进器尾涡的结构。涡的三维空间结构采用Q准则[11]等值面显示,取Q= 5 000。本文中尾涡的计算基于直翼推进器船后水动力载荷预报方法,不考虑自由面的影响,采用大涡模拟方法进行计算。

图12 不同进速系数下船后直翼推进器尾涡结构(e=0.7,Q=5 000)Fig.12 Stern vortex structure of cycloidal propeller under different advance coefficients (e=0.7,Q =5 000)
由图12可以看出,在低进速系数(J=0.2)下,由于来流速度较低,叶片翼型分离出的尾涡会在船尾聚集,同时,在对称面边界上也会附着涡(C框)。随着进速系数的增大(J=1.0),从叶片根部泄落的梢涡迅速向船尾扩散(B框),在高进速系数下(J=1.8),尾涡在向船尾移动的过程中迅速消散,且随着进速系数的增加,湍流迁移速度也随之增大,尾涡在向船舶漂移时会有收缩的趋势。由于直翼推进器叶片做着规律的周期性圆周运动,叶片根部脱落的梢涡会形成半圆形的带状向船尾移动,并与方形船尾分离出的涡(A框)融合在一起。随着来流速度的增加,叶根处诱导的梢涡在扩散的过程中与船舯对称面之间的角度越来越大。同时从图中还可以看出,叶片翼型表面流动分离会产生翼中涡(D框),但是其脱落后会迅速消散。
5 结 语
本文通过分析直翼推进器的工作原理,推导了叶片的多重运动规律公式,然后采用滑移网格技术建立直翼推进器敞水水动力性能数值模拟方法,并与试验值进行对比,验证了该方法的准确性,最后在此基础上研究了船后伴流场对直翼推进器水动力性能的影响。通过研究发现,在敞水条件下,偏心率越大,直翼推进器的推力系数和转矩系数越大,产生正推力的进速系数范围也随之增大;整桨瞬时载荷和单桨叶瞬时载荷变化存在明显的叶频特征,在一定的偏心率下,整桨的主推力和转矩的波动幅值随进速系数的减小而增大;船体伴流对直翼推进器的主推力和转矩影响较小,但侧向力的变化显著。研究结果对于分析直翼推进器的桨叶强度以及进一步研究其水动力性能具有借鉴意义。

