基于SMO算法的中央空调螺杆式压缩机故障自动检测技术

李振坡,李永新

(首都师范大学，北京 100048)

1 引言

中央空调是现代社会不可缺少的电器之一，也是主要的耗能终端之一。据不完全数据显示，跟建筑行业有关的供暖、通风和空调系统所消耗的能源占我国国民经济总能耗的30%左右，并且占比还在不断增加。一般来说，中央空调压缩机发生故障后，还会增加15%-30%的能源消耗，不仅如此，发生故障后的中央空调无法正常工作，导致室内环境舒适度下降，引起业主的不满和投诉。所以，为了保证中央空调的正常工作，对中央空调压缩机实行故障自动检测[1-3]是非常有必要的。

中央空调螺杆式压缩机大多为半密封式，工作马达和压缩机的各个零部件都被封装在同一个机箱内部，在启动中央空调后，蒸汽带来的强大冲击力直接作用于电动机，巨大的温差变化和压力，对中央空调整个运作系统都造成了严重的干扰。与此同时，电机绕组也受启动电源的巨大影响，操作不当就会发生故障。总的来说，中央空调压缩机电机是整个中央空调系统中工作环境最恶劣、最易发生故障的装置。压缩机电机绕组比较脆弱，发生故障的几率较大，且制作工艺非常精细，在发生故障后，对维修人员的技术要求非常高，要及时找准故障发生的部位，运用正确的方式方法，达到合格的维修效果，保证中央空调的工作质量。但是，中央空调螺杆式压缩机故障信号采集过程非常困难，基于此，本文提出了基于SMO(Sequential Minimal Optimization，序列最小优化)算法的中央空调螺杆式压缩机故障自动检测技术。首先针对中央空调螺杆式压缩机设计了故障检测装置，对故障信号进行特征提取，根据不同的故障信号设置其对应的特征向量，构成训练样本和测试样本。另外，利用一对一分类算法测试样本，根据不同的故障信号判断故障发生的部位以及故障类型[4]，实现对压缩机故障的检测。仿真实验结果验证了所提方法可以有效识别故障发生的部位及类型，及时实施针对性的维修策略，保障中央空调的正常运行。

2 中央空调螺杆式压缩机故障检测装置

由于中央空调螺杆式压缩机的信号采集难度较高，尤其是运行中的压缩机，更是难上加难。中央空调压缩机属于旋转类机械，表现出来的故障特征和其他旋转类机械相似，因此，本文设计的故障检测装置带有转轴传动装置、可对振动故障信号频谱进行精准检测，以此获得压缩机在工作时产生的各类故障振动信号。该装置由异步电机为转子转动提供电源，将加速度传感器安装在轴承底座上，来获取转子转动的信号。传感器将获取到的信号经过信号调节器传送至数据采集卡[5]中，选用的数据采集卡采样频率、触发方式和输入范围均符合本文设计的故障检测装置要求。该采集卡的PCI(Peripheral Component Interconnect，外设部件互连标准)总线安装在工控计算机的PCI 插槽中，工控计算机内的Labview软件对压缩机的电压和电流信号进行实时采集、保存与分析等，PCI1710驱动程序则实现了故障检测装置对故障信号的准确检测。在压缩机中，螺杆压缩机主机作为机组中的重要部件，由机体组件、一对相互啮合的阳、阴转子以及轴承、轴封等组件构成，由于所采用的机体内所装置的运动构件具有极高的精度，因此在运转过程中，能够有效避免固体杂物进入机体内而发生故障的情况。

3 中央空调螺杆式压缩机信号特征提取

通过检测装置对中央空调螺杆式压缩机的检测，获得四种检测信号：不平衡、油膜振动、摩擦和正常[6]。利用二阶低通滤波获取时域信号，并通过FFT(Fast Fourier Transform，快速傅里叶变换)算法计算得到某个时间的功率谱。功率谱图如图1(a)-(d)所示(故障检测装置电机转速为1480r/min)。获取到的时域信号幅值量纲用电压V 表示，功率谱量纲以V2S 表示，Labview 软件控制整体采样点数，通常为2 的次方。本文在启动故障检测装置对压缩机进行故障检测时，采样点数值取4096点，时域信号波形取10个波峰波谷。

从图1(a)-(d)的曲线变化可以看出，当压缩机出现油膜振动和摩擦两种故障时，时域信号幅值变化较明显；当出现不平衡故障时，时域信号幅值变化较小。当出现以上三种故障时，可以看出与正常信号在功率谱上的幅值区别很大。在进行故障信号特征提取时，需要先对其特征量[7]进行计算。针对以上三种典型故障，最大的时域信号幅值与各自对应的频率分别记为p1，p2和p3及f1、f2和f3；最大的时域信号和最小的时域信号分别记为A1和A2。特征向量记为：[f1f2f3，p1，p2，p3，A1，A2]T。从图1(a)-(d)提取一组特征数据，记录为表1格式。

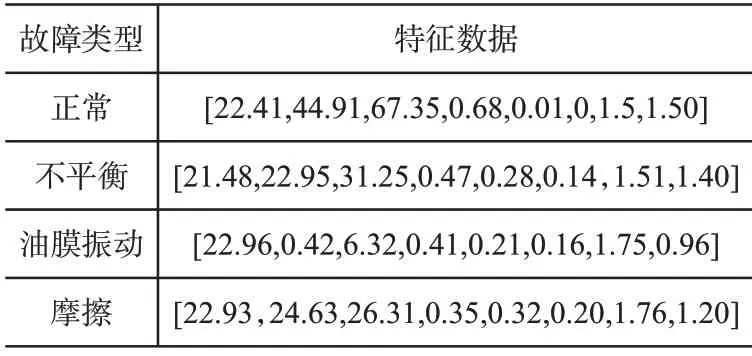
表1 故障识别所需特征数据表

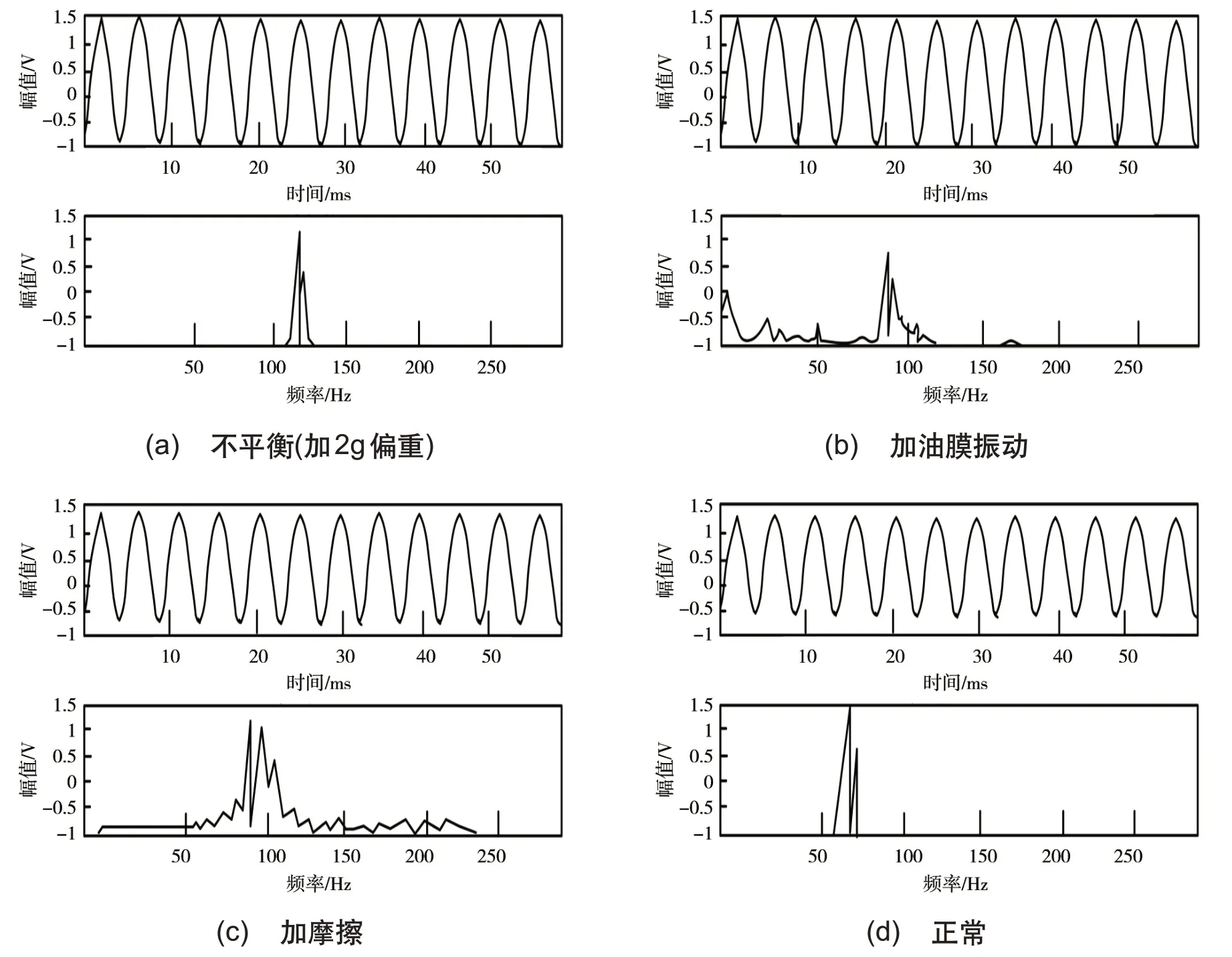
图1 四种典型振动信号功率谱图

在对故障检测装置获取的故障信号[8]进行分析时发现，同类别的故障信号在功率谱上曲线变化不大，只是时域信号幅值略微有些差别。为了方便计算，同时也为了防止故障检测装置出现“过于严格”的现象，将幅值小于0．04V2S的记为“0”，幅值大于等于0．04V2S小于0．2V2S的记为“1”，幅值大于等于0．2V2S小于0．5V2S的记为“2”，幅值大于等于0．5V2S的记为“3”。把频率22．46Hz记为“1”，以此类推。经过简化后的特征向量，记录格式如表2所示。

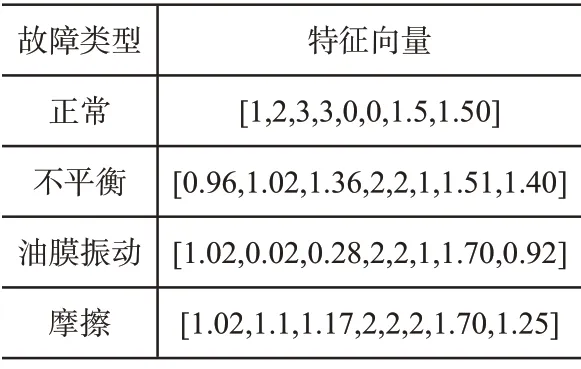
表2 故障识别所需特征向量表

4 SMO算法下中央空调螺杆式压缩机故障自动检测

4.1 构建支持向量机模型

支持向量机(Support Vector Machine，SVM)的基本原理是将待训练数据经过非线性映射投射到指定的高维特征空间内，再在这个空间内建立线性回归函数。SVM 算法原理与正则化原理相关，那么对于观测样本xin，yi，i=1，2，…，l，SVM的原始优化问题可以表示为：

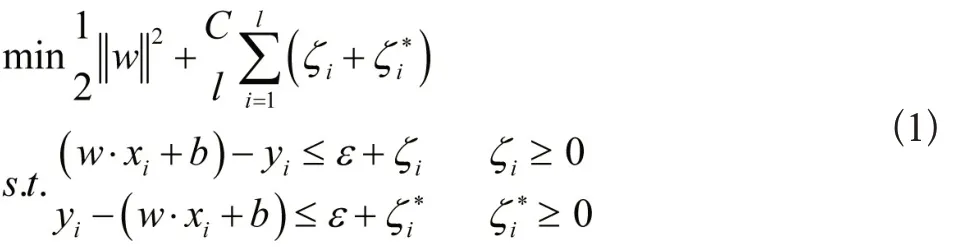
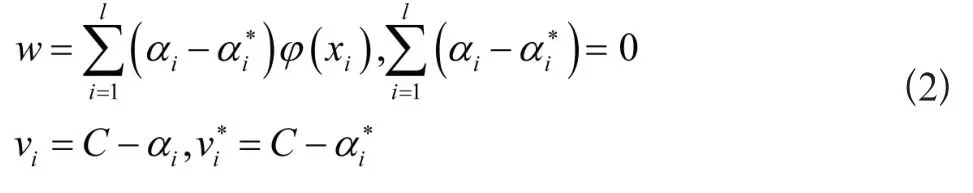
式中，φ( )表示非线性映射。将KKT 条件式(2)代入式(1)中，根据对偶原理[9]和核函数的性质k(x，y)=φ(x)φ(y)，即可得到式(1)的对偶优化问题为：

由式(3)的结果可计算得到SVM的输出为：

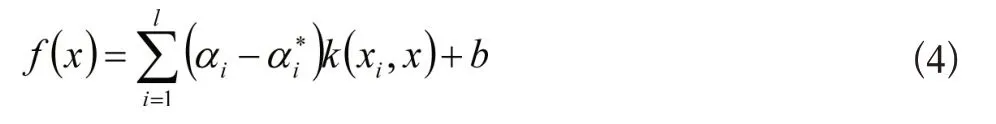
式(4)中，学习机器为ε-SVM，是通过ε-不敏感损失函数计算得到的。

4.2 支持向量机模型训练方法

计算式(3)的方法，就是SVM的模型训练方法，也可将其称为是对受约束凸二次规划的计算问题。SMO算法在处理数量较多的数据时非常高效。SMO 算法的也可理解为：选择两个符合要求的训练点[10]，寻找两个最优变量，规定了停机准则。接下来对SMO 算法做进一步阐述，并对停机准则做了部分改进。

4.2.1 两个训练点的选择

SMO算法对于两个训练点的选择利用两层循环的启发式策略来选择，假设两个优化变量为、。外部循环选择优化变量：在非边界样本中找出与KKT条件相反的样本，如果没有符合条件的样本，就在整个样本集中寻找，如果整个样本集中都没有，直接技术计算。

4.2.2 两个优化变量的解析

为了计算简单，将变量做替换，即：

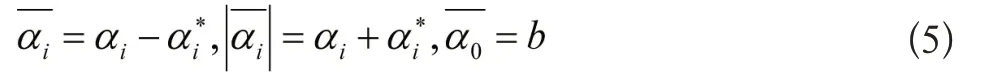
那么式(3)变为：

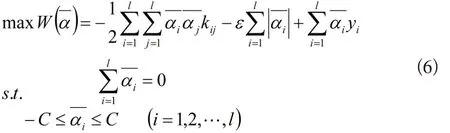
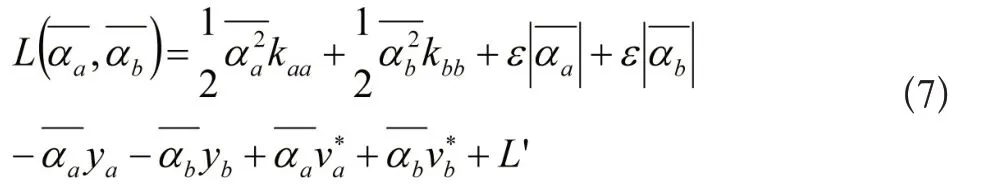
式中：

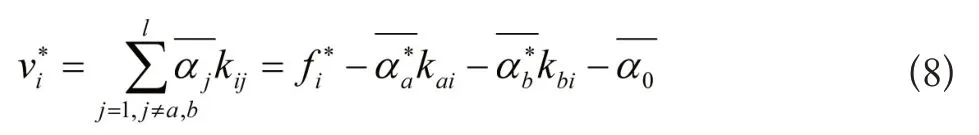
式中，L'表示式(6)中不含αa和αb的项；带有上标“*”的量表示前一次迭代的值[11]。根据优化问题式(3)的约束条件，可以假设：

代入式(7)，并记：

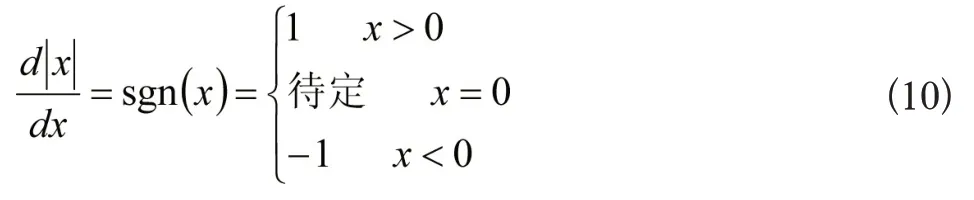
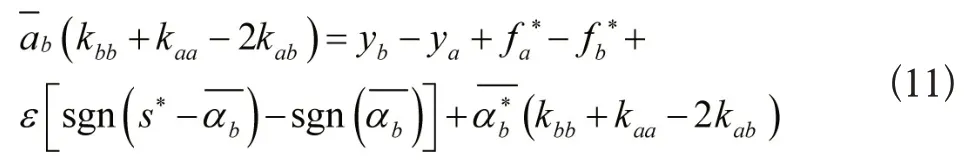
由式(11)可得变量αb的递推计算公式：

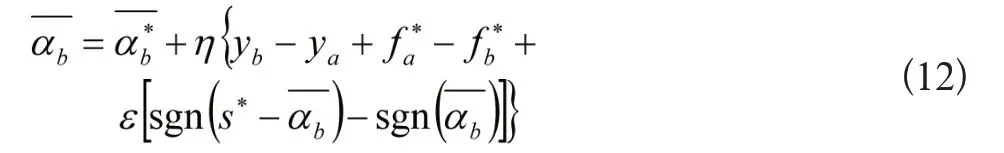
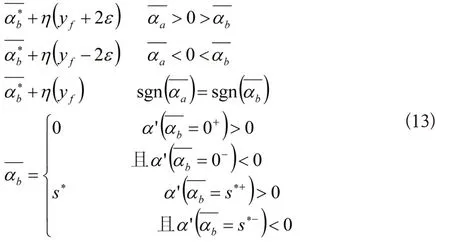
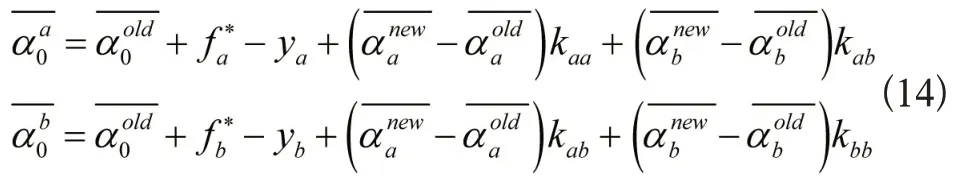
4.2.3 SMO的停机准则

SMO算法的停机准则以KKT条件为约束条件，虽然这种方法可以保证目标函数在计算初期时有着较好的上升速度，但是到了计算后期，计算过程却变得非常缓慢。因此，对SMO 的停机准则做了部分改进。依据最优化理论可知，当对偶函数等于0 时，凸二次优化问题可求得全局最优解，以此对SMO算法的停机准则提出改进：

计算式(3)的可行解α，令

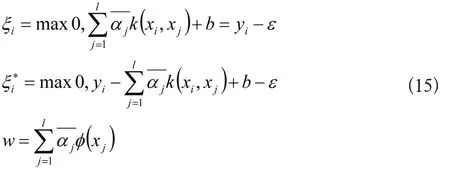
通过计算可知，(w，ξ，b)是式(1)的可行解。使式(1)的目标函数值为u(w，ξ，ξ*，b)，式(3)的目标函数值为W(α)，那么：

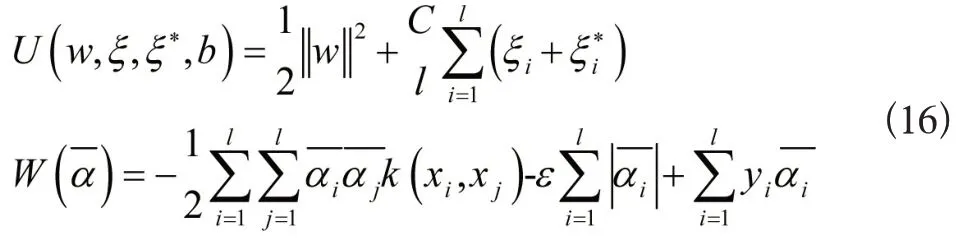
可行解α和(w，ξ，ξ*，b)二者目标函数值相等，即U(w，ξ，ξ*，b)=W()，由此可得：

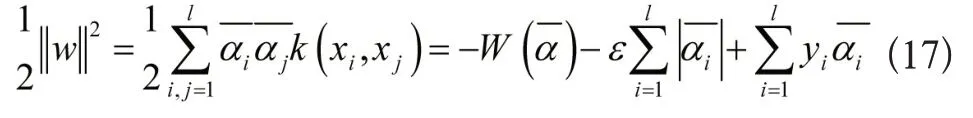
令

则

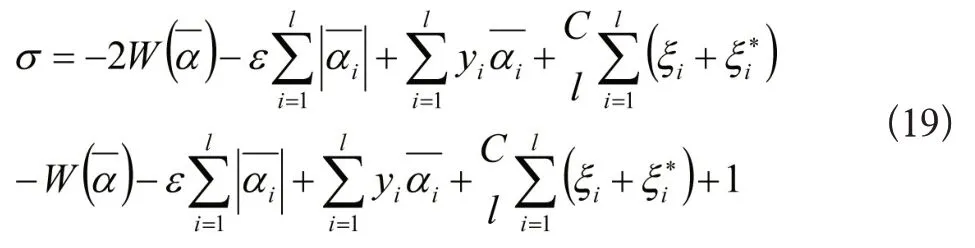
改进后的SMO算法的停机准则为：

(6) 当选择的样本满足了KKT 条件，或者σ的值小于SVM算法精度要求，即可输出α，结束计算；否则重复步骤(2)继续寻找优化变量。

4.3 故障自动检测实现

由于支持向量机分类器是一个二元分类器，在对各种类型的故障进行诊断过程中，要实现精准识别，此时就需要构建一个多元分类器来对不同类型的故障进行识别。通常将2个分类器合二为一，实现多值分类器的分类，构建多元分类器主要有以下几种方法：一对一分类算法(one-against-one，1-v-1)，一对多算法(one-versus-rest，1-v-r)和最小输出编码法等。根据本文的要求，这里选用一对一分类算法。其基本思想是：对分类器建立N(n-1)/2 个SVM，每2 个分类器之间通过1 个SVM 训练。这种方法计算简单，效果比较明显。

根据振动故障检测装置检测到的四种信号频率，建立6个SVM 分类器。SVM1 分类正常信号与油膜振动信号，SVM2分类正常信号与不平衡信号，SVM3分类正常信号与摩擦信号，SVM4分类不平衡信号与油膜振动信号，SVM5分类不平衡信号与摩擦信号，SVM6分类油膜振动信号与摩擦信号。通过6 个SVM 分类器的训练结果，获得最优分类函数。在实际运用过程中，将6 个SVM 分类器的“票数”分别进行统计，哪一个SVM分类器的“得票”最多，即可判定中央空调压缩机处于哪种故障状态下。

5 仿真实验

为了验证本文方法对压缩机故障的检测能力，实验采用首都师范大学螺杆机组维修数据为测试样本，用训练后的分类器对60个测试样本进行仿真实验验证。

故障检测装置对分类器诊断结果和故障识别结果如表3和表4 所示。由于SMO 算法对优化变量的高效率求解，使得本文所提的故障检测技术对压缩机故障具有较高的泛化能力，且故障诊断结果和故障识别均显示较优，可以实现对中央空调螺杆式压缩机故障的自动检测。

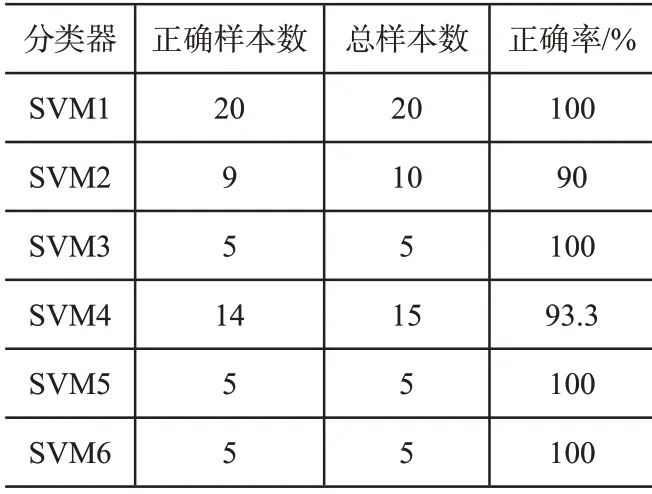
表3 故障诊断结果

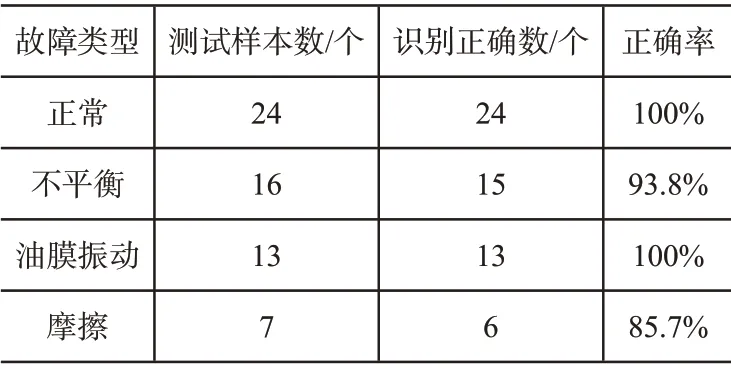
表4 故障识别结果

6 结束语

针对中央空调螺杆式压缩机典型的四种振动信号频率，本文设计了故障检测装置，利用Labview 平台，对故障信号进行时频分析，通过一对一方法构建多元分类器，实现了在样本不多的情况下完成对分类器的学习训练，且泛化能力较强。通过仿真实验结果表明，本文方法诊断效率较高，且故障诊断结果准确率较高，适合压缩机的故障识别。