基于主客观赋权法-TOPSIS的双刀车削参数多目标优选

孙捷夫，杨巍

1沈阳飞机工业(集团)有限公司；2哈尔滨工程大学

1 引言

随着低碳理念的大力发展，航空零件设计原则逐渐向轻质高效转变[1]，在满足功能特性的同时最小化动力消耗，相应的结构设计优选薄壁特征，材料优选轻质材料。LF2铝合金垫环零件是航空轻量化设计的典型产品，在功能要求方面，该零件在飞机各系统中起到重要的尺寸配合和流量控制作用；在设计要求方面，其结构为有φ4mm中心孔的圆环，零件典型直径φ10mm，典型厚度为0.2mm，要求加工后两端面的最大距离不大于0.3mm，表面粗糙度不高于Ra0.8μm；在能耗要求方面，为响应低碳理念，单件零件机械加工所需功率越小越优。

为满足上述要求，LF2铝合金垫环需要解决一些机械加工问题：从结构角度，由于厚度薄、刚性差，加工变形严重；从材料角度，由于LF2铝合金塑性大、热稳定性差[2]，表面粗糙度难以控制；从工艺角度，LF2铝合金属于有色金属，采用磨削类加工方法会堵塞砂轮，无法在平面磨床上批量加工，仅能在数控车床上进行单件加工，很难降低加工单件零件所需功率。

LF2铝合金垫环零件的车削加工本质上属于低刚度类零件的机械加工，目前国内外尚无可直接应用于LF2铝合金垫环零件的研究成果，部分学者关于低刚度类零件的研究成果具有一定参考意义。于金等[3]和杨中宝等[4]通过设计特定结构的专用夹具提高了工艺系统刚性，苏晓等[5]和江敏等[6]通过设计特定几何形状专用刀具来降低切削外力，上述方法均可一定程度改善低刚度零件加工质量，但都具有通用性差及制造成本高的问题。李忠群等[7]和冯新敏等[8]采用智能优化算法探索了低刚度零件的最优加工参数，但存在加工目标单一及优化结果不稳定等问题。薛国彬等[9]和孙捷夫等[10]等针对不同的加工需求，对典型低刚度零件加工参数进行了多目标优化，虽取得一定效果，但其实现过程基于单目标拟合模型，存在拟合误差且计算过程复杂。

目前研究成果均有特定的适用对象，无法准确指导LF2铝合金垫环零件车削加工。本文以LF2铝合金垫环零件为研究对象，以提质提效为目标，提出双刀车削工艺及加工参数多目标优选方法，并给出具体实施步骤。

2 双刀车削加工关键影响因素

2.1 双刀车削加工模型

常规加工方法无法高质高效实现LF2铝合金垫环零件车削加工，根本原因在于车削过程中随刀具的径向进给，垫环零件在毛坯上的剩余尺寸相应减少，已完成切削的垫环零件和待切削的毛坯部分组成的工艺系统刚性呈非线性急剧降低，以轴向切削力为主的外部因素打破垫环零件内部的力学平衡，垫环零件会相应产生振纹或变形现象，导致难以满足质量要求。

针对上述分析提出双刀车削工艺，即利用两把相同的槽刀在LF2铝合金垫环零件两端面同时、同向、同速进行无余量切削，一次进给完成全部切削。双刀车削工艺的本质是基于力学平衡思想，降低外部因素影响，提高工艺系统的刚性，进而提升加工质量。双刀车削加工现场照片如图2所示。

图1 双刀车削加工现场

图2 双刀车削工艺受力分析

2.2 关键影响因素分析

在加工变形方面，两把相同槽刀对称安装、同向同速进给，实现零件的径向切削，分别产生进给力F1y和F2y。理论情况下，两把槽刀分别作用于垫环零件两端面大小相等、方向相反的切向力F1x，F2x和背向力F1z，F2z在数值上可相互抵消，并作为辅助支撑可提高零件的刚性，减小加工变形，只有进给力为垫环零件产生变形的主要外因。但实际应用中，由于安装误差、刀具磨损和余量不均等原因，两把槽刀作用于垫环零件两端面的切向力和背向力之间会产生一定微小偏差，而在零件材料特性、刀具几何形状和切削加工环境既定的情况下，切向力和背向力偏差以及进给力的数值主要取决于加工参数。

在表面粗糙度方面，传统车削方法由于垫环零件轴向尺寸远小于径向尺寸，零件刚性差导致加工过程伴随剧烈的振动，进而在零件表面产生振纹，增大表面粗糙度，双刀车削工艺通过力学平衡，两把刀具互为支撑，可有效避免由于切削振动导致表面粗糙度的增大。

在功率消耗方面，根据文献[11]可知，切削过程所需功率是零件制造全周期的主要能耗来源，其数值主要取决于主切削力和切削速度，通过合理调整上述两项参数即可有效控制切削功率大小。

因此，优化加工参数是改善垫环零件加工变形和表面粗糙度两项加工质量指标的根本方法，也是直接决定切削功率高低的关键因素。

2 双刀车削试验方案

2.1 试验条件

试料材料牌号LF2，材料状态为M状态；机床选用哈挺GS200型号数控车床，装夹方式为三爪卡盘，冷却方式为乳化液冷却；刀具材料为高速钢，两把槽刀的前角25°，后角18°，副偏角8°，刃倾角0°，刀尖圆弧半径0.2mm；要求加工后垫环零件两端面最大距离L不大于0.3mm，表面粗糙度Ra不大于0.8μm；两端面最大距离L采用分度值为0.02mm的游标卡尺测量，采用苏州天萨RUGOSURF90G便携式粗糙度测量仪测量表面粗糙度，采用HC33C型功率传感器测量切削功率。

2.2 试验设计及试验结果

双刀车削加工试验设计方案采用中心复合试验设计法，该方法归属于响应曲面试验设计法，相比常规的正交试验法等试验设计法，能更准确地表达试验数据的非线性[12]；相比同归属于响应曲面设计法的Box-Behnken试验设计法，引入旋转因子概念，可探究变量在极值点或外延点处的切削性能，试验数据分布更均匀，能更全面地表达试验结果的预测性。

综合考虑刀具特性和设备参数，限定切削速度v=20～60m/min，进给量f=0.02～0.1mm/r，由于双刀车削工艺采用无余量切削，背吃刀量不作为加工变量。设定旋转因子为1.414，中心点重复次数为2次，中心复合试验设计矩阵及试验结果如表1所示。

表1 试验设计矩阵及试验结果

2.3 试验结果分析

采用极差法对表1的试验结果进行分析，结果分别见表2、表3和表4。其中，表示因素i在j水平时的粗糙度平均值，极差表示第i个因素的极差，某变量极差越大，代表该变量对结果影响越显著。

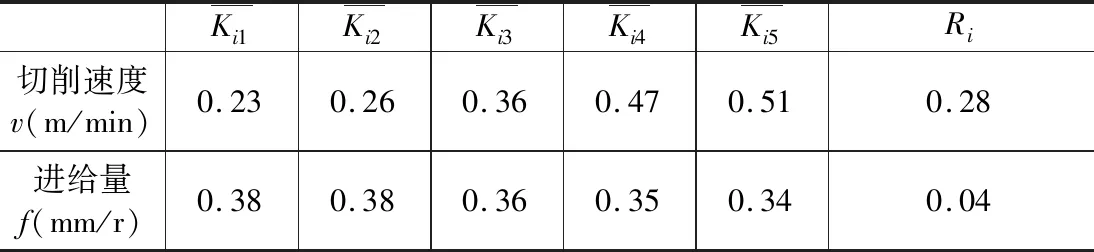
表2 车削参数对两端面最大距离L的极差分析结果

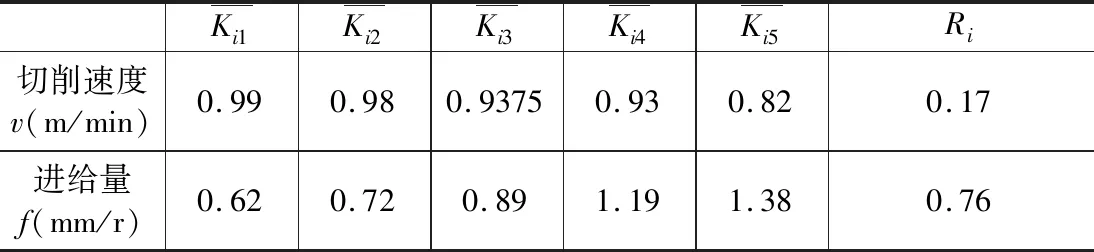
表3 车削参数对两表面粗糙度Ra的极差分析结果

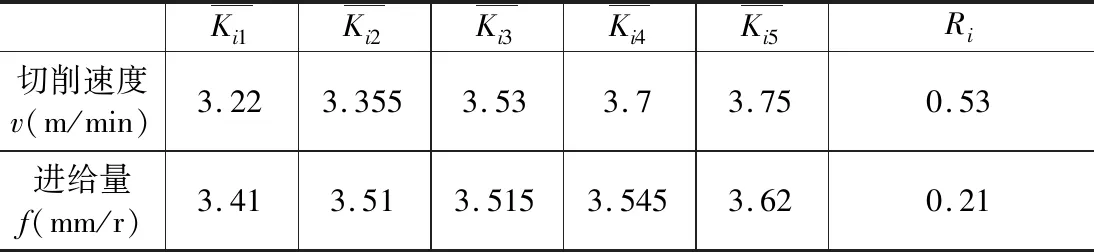
表4 车削参数对切削功率P的极差分析结果

由表2可知，两端面最大距离L受切削速度影响较大，呈正相关，该现象是由于随切削速度增大，加工过程中受到离心力和切削力综合作用的影响也随之增强，增加了零件变形量；进给量两端面最大距离L的影响较小，总体呈负相关，该现象是由于随进给量增大，切削厚度相应增大，切屑变形系数减小，整体切削力降低，有利于抑制零件加工变形。

由表3可知，表面粗糙度Ra受进给量影响较大，呈正相关，该现象是由于随进给量增大，两槽刀作用于垫环零件两端面的进给量显著增大，由作用力数值差异产生的切削振动效应相应被放大，增大了表面粗糙度，该现象符合金属切削一般规律；切削速度对Ra影响较小，呈负相关，该现象是由于随切削速度的提高有利于抑制积屑瘤的产生，在一定程度上可降低表面粗糙度。由表4可知，切削功率受切削速度影响较大，呈正相关，受进给量影响较小，呈正相关，该现象符合功率计算基本原理。

3 双刀车削参数优选

3.1 基于主客观赋权法的权重分配

为得到满足实际需求的最优车削参数，综合以层次分析法为代表的主观赋权结果和以熵权法为代表的客观赋权结果，对三项评价指标进行权重分配。

(1)基于层次分析法的主观权重分配

层次分析法[13]的核心思想是通过定性和定量分析，将人的主观评价转化为各项指标的权重系数。主要步骤如下：

①构建判断矩阵。基于Saaty的1～9级标度法，将垫环零件加工需求作为上层准则，将两端面最大距离L，表面粗糙度Ra，切削功率P作为评价指标，构建两两比较的判断矩阵，有

(1)

式中，rij(i=j=1，2，…，n)为两个评价指标的相对重要程度数值。

②计算评价指标权重值。先将评价矩阵R进行归一化，并将归一化后的矩阵按行相加后求取特征向量，即为各评价指标的权重系数wi，计算过程如下

(2)

(3)

(4)

③一致性检验。为验证所得权重系数之间是否矛盾，需进行一致性检验。首先根据式(5)计算最大特征根，并根据式(6)计算一致性指标CI，若其与随机一致性指标RI的一致性比率小于0.1，则认为权重系数通过一致性检验。

(5)

(6)

根据上述步骤得出基于层次分析法的权重系数为w1=[两端面最大距离L，表粗糙度Ra，切削功率P]=[0.43，0.38，0.19]，其一致性比率为0.016小于0.1，通过一致性检验。

(2)基于熵权法的客观权重分配

熵权法[14]的核心思想是根据变量对评价指标取值的不确定性概率决定该指标的权重系数，不确定概率越大，信息熵越高，权重系数越小。主要步骤如下：

①构建决策矩阵。基于表1的信息，根据两项车削参数对三项评价指标的试验结果建立决策矩阵，有

(7)

式中，qij为第i项车削参数对第j项评价指标的试验结果(i=1，2，…，m；j=1，2，…，n)。

②决策矩阵规范化处理。本文的三项评价指标均为负向型指标，即越小越好。对式(7)中各数值进行规范化处理，得到sij为

(8)

(9)

③计算评价指标权重值。根据式(10)计算各指标的熵值，再根据式(11)计算各指标权重系数。

(10)

(11)

根据上述步骤得出基于熵权法的权重系数为w2=[两端面最大距离L，表粗糙度Ra，切削功率P]=[0.49，0.42，0.09]。

(3)基于乘法归一法的主客观赋权法权重分配

为强化主观评价的经验优势和客观评价的客观优势，对两种方法得到的权重系数进行相乘，并进行归一化处理，有

(12)

根据主客观赋权法的权重分配结果w=[两端面最大距离L，表粗糙度Ra，切削功率P]=[0.54，0.41，0.05]，三个指标按重要程度依次为两端面最大距离L>表粗糙度Ra>切削功率P。上述排序符合实际工程需要，垫环零件两端面最大距离L是决定其使用性能的核心指标，若该指标不满足需求，后续需设计专用工装对其进行修正，需要增加大量的时间成本和经济成本；表面粗糙度Ra对其使用性能具有直接影响，若其不满足需求，后续需采用钳工抛光等方法进行修正，需要一定的时间成本和人工成本；虽然切削功率P不影响加工质量，但其间接决定加工成本和能耗指标的符合程度。

3.2 基于TOPSIS的车削参数优选

TOPSIS法[15]作为简单、高效的多目标决策方法，通过计算各样本点与理想解之间的距离选出最优方案。主要步骤如下：

①构建加权矩阵。由式(9)得出的规范化矩阵元素S=(sij)m×n与式(12)得出的权重系数相乘，构建加权矩阵V为

(13)

②确定正负理想解。针对垫环零件加工问题，正理想解即各指标的最小值负理想解即各指标的最大值

③计算欧式距离，有

(14)

(15)

④计算评价值，有

(16)

根据上述步骤计算，得出表1中序号6的车削参数为满足三项评价指标的最优加工参数。

3.3 实际加工对比验证

为验证基于双刀车削工艺的最优加工参数准确性，对LF2铝合金垫环零件进行实际切削加工验证，并对比选用经验参数的传统工艺法和基于极差法的单目标最优参数加工结果，结果如表5所示。

表5 最优加工参数实际验证结果

根据实际加工验证结果可知，仅有基于本文方法得出的最优车削参数对三项评价指标的综合性能最优。

4 结语

(1)针对垫环零件的车削加工提出了双刀车削工艺，并得出车削参数是影响双刀车削工艺加工结果的核心因素。

(2)基于中心复合试验设计法建立切削试验矩阵，试验结果表明，两端面最大距离L受切削速度影响较大，呈正相关；受进给量影响较小，呈负相关；表面粗糙度Ra受进给量影响较大，呈正相关；受切削速度影响较小，呈负相关；切削功率P受切削速度影响较大，呈正相关，受进给量影响较小，呈正相关。

(3)基于乘法归一法综合层次分析法和熵权法的计算结果，得出各评价指标的主客观赋权系数为w=[两端面最大距离L，表粗糙度Ra，切削功率P]=[0.54，0.41，0.05]，三个指标按重要程度排序为两端面最大距离L>表粗糙度Ra>切削功率P。通过TOPSIS方法选出最优加工参数为v=20m/min，f=0.02mm/r，经实际加工验证，本文提出的方法相比传统基于加工经验和单目标加工参数的方法均取得更好的综合表现。