地铁小半径曲线不同位置轮轨摩擦因数优化

朱爱华,张 帆,孙培文,张凯琦,2,杨建伟,马潮潮,孟宇轩

(1.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室,北京 100044;2.山西江淮重工有限责任公司,山西 晋城 048026)

地铁线路复杂多变,小半径曲线频繁出现,地铁列车在行驶过程具有加速制动频繁的特点,车轮作为承载单元直接与轨道接触,极易产生磨耗和表面损伤,影响列车的正常行驶,增加了后期维护的成本。其中轮轨磨耗问题尤为突出,在实践操作中通常会在轮轨间添加不同种类的润滑材料,以降低轮轨摩擦因数,从而降低轮轨磨耗与表面损伤。目前对于轮轨减磨的研究主要集中在线路参数和摩擦因数控制等方面。在线路参数方面,国内外学者的研究主要集中在曲线半径、线路超高、轨距变化、轨底坡和缓和曲线长度等参数对轮轨磨耗与疲劳损伤性能的影响。周坤等[1]通过仿真得到了重载货车曲线半径越小,其轮轨磨耗和疲劳损伤越严重的规律,建议重载货车最小曲线半径为1 200 m,困难情况时取800 m;杨春雷等[2]基于非线性轮轨蠕滑理论,分析了缓和曲线长度和外轨超高等曲线几何参数对重载货车轮轨动力学和磨耗的影响;王志强等[3]通过车辆-轨道耦合模型计算了不同曲线半径下钢轨磨耗的分布范围、磨耗程度及变化规律;周黄标等[4]通过建立车辆动力学模型,分析了线路超高与轨距加宽对轮轨磨耗的影响,研究表明适当的欠超高可以减轻轮轨磨耗,不必要的轨距加宽会导致异常磨耗;侯茂锐等[5]通过磨耗跟踪测试与仿真相结合的方式,研究了曲线半径、轨距加宽和摩擦因数对高速动车组钢轨磨耗的影响;杨广雪等[6]和杨光等[7]通过建立全弹性化车辆动力学模型,分析了摩擦因数、轮对内侧距和轨底坡对高速列车轮轨磨耗的影响;徐凯等[8]仿真分析了线路参数设置与钢轨打磨对高速铁路小半径曲线钢轨侧磨的影响,研究表明外轨摩擦因数0.2、轨距加宽5～10 mm、轨底坡增加1/20最有利于减缓钢轨侧磨;张建全等[9]分析了车辆在缓和曲线上的受力情况,研究了缓和曲线线型对车辆动力学性能的影响;寇杰等[10]通过线路跟踪测试与动力学软件仿真相结合的方式分析了城际动车组在非均衡速度下通过小半径曲线时的磨耗特性,结果表明非均衡速度与小半径曲线耦合会加剧车轮轮缘磨耗。在摩擦因数控制方面,国内外学者主要研究了在不同外界环境和润滑方法下摩擦因数控制对轮轨磨耗及疲劳的影响。肖乾等[11]将动力学仿真结果带入轮轨稳态滚动接触有限元模型中,研究不同摩擦因数对轮轨磨耗量及其分布的影响,结果表明摩擦因数的增大不仅会使接触区磨耗量变大,而且会改变分布规律,当摩擦因数大于0.2时,磨耗区由轻微磨耗区转化为中度磨耗区;王平等[12]通过建立车辆-道岔耦合动力学模型,分析了摩擦因数匹配对尖轨磨耗的影响,研究表明轮轨摩擦因数控制可以降低尖轨磨耗,且双侧轮轨润滑的效果优于单侧润滑;温静等[13]通过有限元软件与动力学软件相结合的手段分析了摩擦因数对地铁小半径曲线接触应力和滚动疲劳特性的影响;Tomeoka等[14]通过实验室模拟试验研究了不同摩擦改进剂对轮轨匹配的影响规律,提出摩擦控制剂可以通过降低摩擦因子从而大幅减少车轮磨耗;李亨利等[15]通过建立车辆动力学模型,分析了不同轮轨摩擦控制方法对重载货车轮轨磨耗的影响,研究表明轨侧+轨顶润滑可以显著降低轮缘磨耗与钢轨侧面磨耗;Zhu等[16]通过销盘滑动摩擦试验研究了温湿度对摩擦因数和轮轨磨耗的影响,结果发现轮轨的温度和周边的湿度可以很大程度地改变轮轨的磨耗性能;任声泰[17]指出轮缘喷洒润滑介质可以有效地降低轮轨接触表面的摩擦因数,从而减少车轮的轮缘磨耗,同时可提高列车的曲线通过安全性。

以上研究主要集中在线路参数和轮轨摩擦因数控制两方面对车轮磨耗的影响,针对地铁车辆在同一条曲线线路不同位置的轮轨磨耗、滚动接触疲劳特性和曲线通过安全性与摩擦因数的关系的研究鲜有涉及。笔者以小半径曲线不同位置为切入点,通过实际参数建立某地铁B型车动力学仿真模型,分析不同摩擦因数下曲线不同位置的车轮磨耗性能、滚动接触疲劳特性以及曲线通过安全性,并通过熵权法对上述3个指标进行曲线不同位置的轮轨摩擦因数优化,为地铁小半径曲线润滑控制提供技术支持。

1 地铁动力学仿真模型

1.1 车辆动力学模型

通过多体动力学仿真软件SIMPACK建立国内某地铁车辆动力学模型(图1),主要建模参数[18]见表1。全车包括1个车体、2个构架、4对轮对和8个轴箱。车轮型面为LM型踏面,车轮直径840 mm,钢轨选用UIC60轨,轨底坡为1/40,轨距为1 435 mm,轨距不加宽,列车运行的平均速度为60 km/h。

图1 车辆动力学模型Fig.1 Vehicle dynamics model

表1 某地铁车辆主要参数Table 1 Main parameters of a subway vehicle

1.2 线路设置

受建设条件的限制,地铁线路中小半径曲线占比较大。根据《地铁设计规范》GB 50157—2013,选取轨距不加宽情况下的最小曲线半径R300的曲线作为研究对象。设置全长为1 000 m的右转C型曲线,即右侧车轮为内侧车轮,线路由直线、缓和曲线、圆曲线、缓和曲线和直线依次连接而成,不考虑轨道不平顺的情况,线路具体参数如表2所示。

表2 线路组成及线路参数Table 2 Line composition and line parameters

1.3 曲线不同位置划分

为研究小半径曲线不同位置处的轮轨磨耗、疲劳损伤和安全性指标的情况,将R300 C型曲线分为6个观测点,分别为直线点、第1段缓和曲线中点(缓中点1)、缓圆点、曲中点、圆缓点、第2段缓和曲线中点(缓中点2),结果如图2所示。其中缓圆点和圆缓点位于缓和曲线和圆曲线的连接处,设定前后各取20 m(总长40 m)为该点的区间,其余各点的区间均是在自己所在的线型上取长度40 m,各点的位置与长度如表3所示。

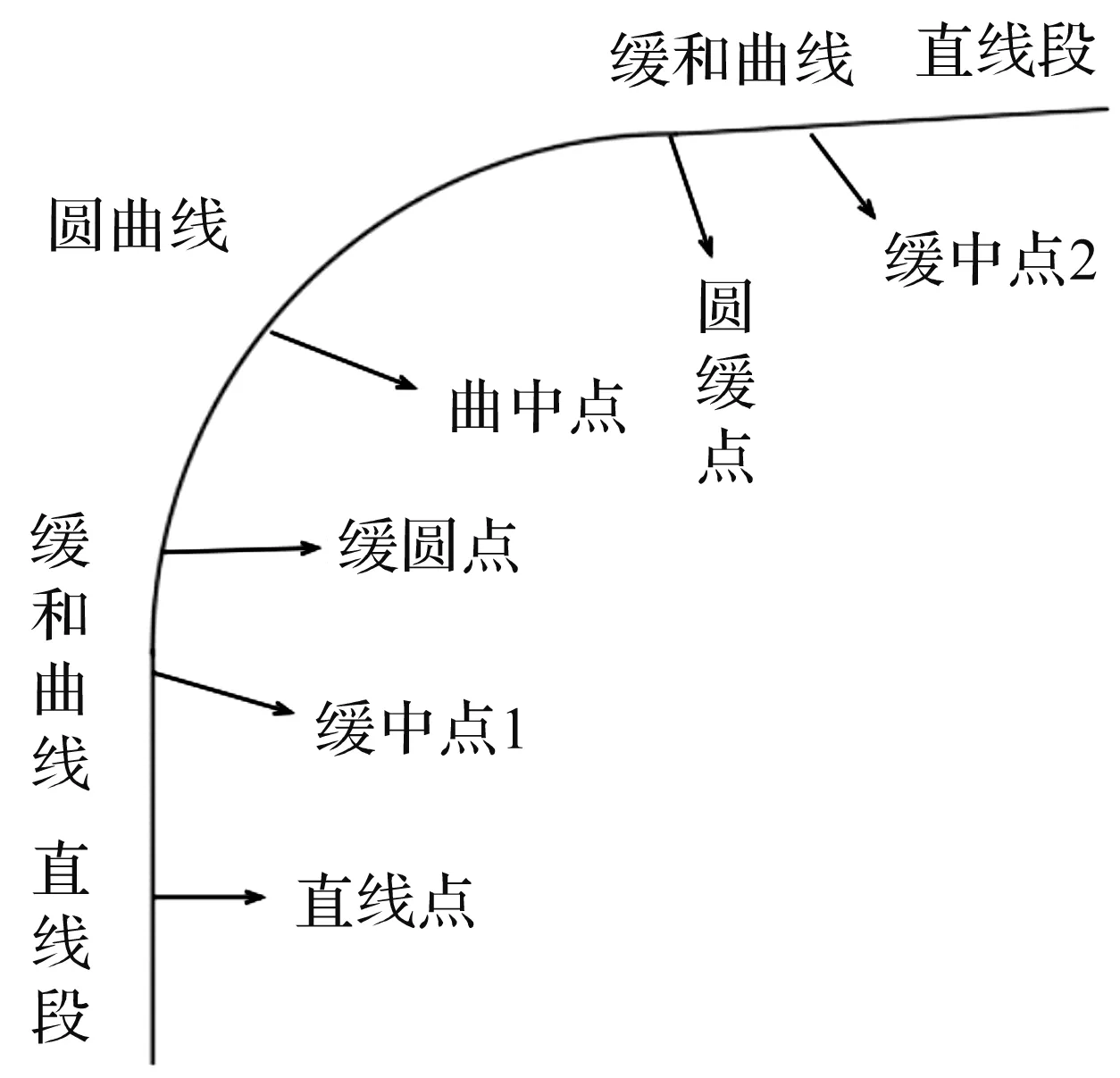
图2 曲线位置划分图Fig.2 Curve location division diagram

表3 曲线不同位置参数Table 3 Different position parameters of the curve

1.4 Elkins磨耗指数

采用Elkins磨耗指数评价车轮磨耗性能。Elkins磨耗指数综合考虑了车轮蠕滑率,其数值更接近于实际磨耗程度,数值越大说明轮轨磨耗越严重,其计算式为

W=Txξx+Tyξy

(1)

式中:W为磨耗指数;Tx,Ty分别为横纵向蠕滑力,N;ξx,ξy分别为横纵向蠕滑率。

1.5 滚动接触疲劳

采用Ekberg等[19]提出的表面疲劳指数(FIsurf)评价车轮滚动疲劳特性。如果计算得到的表面疲劳指数大于0,则说明车轮处于安定图中的棘轮效应区,在与轨道接触的过程中可能发生塑性变形,导致车轮失效的概率增加,其计算式为

(2)

式中:Tx,Ty分别为横纵向蠕滑力,N;Fs为轮轨法向力,N;a,b分别为椭圆接触斑长短半轴的长度,mm;k为车轮材料纯剪切屈服强度,取303 MPa。

1.6 车辆安全性指标

采用脱轨系数评价车辆安全性,其计算式为

(3)

式中:Q为轮轨垂向力,N;P为轮轨横向力,N。

2 基于熵权法的指标综合评价

磨耗指数、表面疲劳指数和脱轨系数分别作为车轮磨耗特性、疲劳特性和曲线安全性的评价指标,每个指标受摩擦因数影响的规律各不相同,很难直观地得出优化结果,需要借助综合评价方法将多指标问题按照一定规则转换为单指标问题,再通过线性加权的方法得到一个综合得分,从而实现对摩擦因数的优选。其中加权系数的选取对最终优化结果起着重要的作用。熵权法是目前工科领域中应用最广泛的客观赋权法[20-21],适用于多目标和多指标的优化问题,根据指标的相对变化程度对系统整体的影响来决定指标的权重,即根据各个指标标志值的差异程度进行赋权,其计算结果的准确度较高,且更具有客观性,笔者选取的3个评价指标分别从3个不同维度衡量摩擦因数的优劣,这3个维度同等重要,所以在权重系数的赋予上需要更多地考虑数据本身的变化对结果的影响,这与熵权法相吻合,故采用基于熵权法的综合评价方法进行曲线不同位置的摩擦因数优化。

2.1 熵权法基本原理

熵权法是一种依赖于数据本身变化规律的客观赋权法,其指标权重的大小根据数据本身变化特性进行权重赋予,若某一指标的信息熵越小,则说明该指标的样本变化越剧烈,提供的信息量越大,其权重系数也就越大。

2.2 熵权法具体步骤

选取的磨耗指数、表面疲劳指数和脱轨系数3个评价指标的量纲、单位不同,其数值均是越小越好。先对仿真得到的数据进行负向指标0～1归一化处理,将各项评价指标统一到[0,1]区间,其计算式为

(4)

式中:xij为第i个摩擦因数数据组的第j个指标;x′ij为归一化后处理得到的结果;max(xj),min(xj)分别为第j个指标下的最大值和最小值。

首先,定义第j项指标下第i个样本所占该指标的大小为yij,其计算式为

(5)

然后,对归一化后的评价指标求信息熵值和信息熵冗余度,其计算式分别为

(6)

dj=1-ej

(7)

式中:ej为第j个指标的熵值,且需要满足k=1/ln(n)>0,ej≥0;dj为第j个指标的信息熵冗余度。

最后,根据3个评价指标的熵值计算相应的权重系数,第j个指标的权重系数为

(8)

式中wj为某一评价指标的权重系数。

得到不同评价指标的权重系数后,通过加权求和的方法得到各个位置在不同摩擦因数下的综合得分s,为摩擦因数优化提供依据,其计算式为

(9)

3 计算结果分析

建立车辆系统动力学模型,设置总长为1 000 m的右转C型R300曲线,以导向轮左侧车轮即外侧车轮作为研究对象,分析当摩擦因数为0.10～0.50时外侧车轮在曲线不同位置的磨耗指数、表面疲劳指数和脱轨系数的变化规律。

3.1 摩擦因数对曲线不同位置磨耗指数的影响

磨耗指数直接反映了轮轨间的磨耗情况,将车轮通过小半径曲线不同位置区间的磨耗指数均方根值(有效值)作为该位置轮轨磨耗性能的评价指标,结果如图3所示。

图3 不同摩擦因数下的磨耗指数有效值Fig.3 Effective value of abrasion index under differentfriction coefficients

由图3可知:曲线不同位置的磨耗指数随着摩擦因数的增大均呈现出先增大再减少的趋势,且均在0.30～0.40时取得最大值。不同位置磨耗指数最大值及对应的摩擦因数见表4。当摩擦因数为0.10～0.50时,缓圆点的磨耗指数有效值最大,缓中点1处的数值最小；当摩擦因数为0.4时,缓圆点的磨耗指数有效值是缓中点1处数值的2.26倍。

表4 曲线不同位置磨耗指数有效值的最大值情况Table 4 The maximum value of the effective value of thewear index at different positions of the curve

为了定量分析曲线各测点的磨耗性能,在图3的基础上,计算摩擦因数在0.1～0.5变化时各测点磨耗指数有效值的平均值,结果如图4所示。

图4 各测点不同摩擦因数下的磨耗指数均值Fig.4 The mean value of the wear index under differentfriction coefficients at each measuring point

由图4可知:各测点的磨耗指数有效值的均值从小到大依次为直线点、缓中点1、缓中点2、曲中点、圆缓点和缓圆点。这说明车轮在圆曲线与两段缓和曲线连接处的磨耗特性最差,需要在缓圆点和圆缓点进行适当的润滑以减少车轮磨耗,延长车轮寿命。

3.2 摩擦因数对曲线不同位置表面疲劳指数的影响

表面疲劳指数反映了车轮的滚动疲劳特性,通过SIMPACK计算不同摩擦因数下车辆通过曲线时的蠕滑力、法向力和接触斑面积,代入式(2)计算出表面疲劳指数,并选取疲劳指数最大值作为疲劳损伤的评价指标,得到不同曲线位置的表面疲劳指数最大值随摩擦因数的变化图,结果如图5所示。

图5 不同摩擦因数下的表面疲劳指数最大值变化图Fig.5 Change graph of the maximum surface fatigue indexunder different friction coefficients

由图5可知:直线点的不同摩擦因数下的表面疲劳指数最大值均小于0,说明车轮在直线段处发生滚动接触疲劳的概率极低,不需要润滑来抑制疲劳裂纹的萌生;曲线其余位置的表面疲劳指数随着摩擦因数的增大均呈现出由负到正逐渐变大的规律,且当各测点的表面疲劳指数首次大于0时所对应的摩擦因数各不相同,其具体数值见表5。当摩擦因数为0.10～0.40时,缓圆点处的数值最大,圆缓点次之;当摩擦因数为0.45～0.50时,圆缓点的数值最大,缓圆点次之。

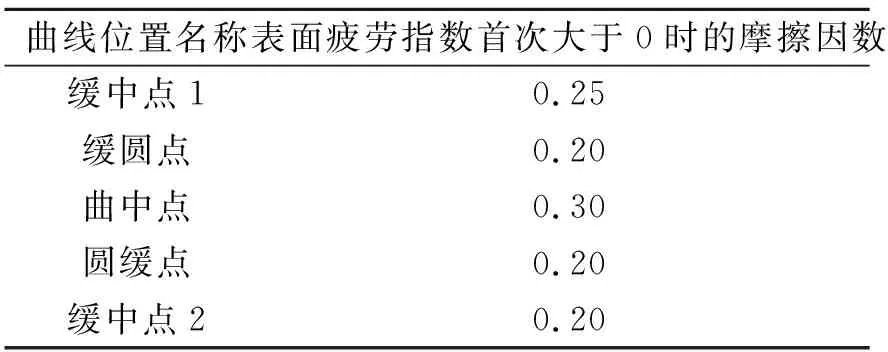
表5 曲线不同位置的表面疲劳指数的最大值和变化情况Table 5 The maximum value and change of the surface fatigueindex at different positions of the curve

3.3 摩擦因数对曲线不同位置脱轨系数的影响

脱轨系数是曲线安全的重要指标,计算车辆通过曲线不同位置时的脱轨系数,并以脱轨系数最大值作为评价指标,结果如图6所示。由图6可知:随着摩擦因数的增加,曲中点的脱轨系数最大值均呈现出逐渐变大的规律,在摩擦因数为0.5时取得最大值0.315 1,其余位置随着摩擦因数的增大呈先增大后减少的规律,且均是在摩擦因数为0.30～0.04时取得最大值,其最大值情况见表6。比较曲线各位置之间的脱轨系数最大值情况,当摩擦因数为0.10～0.25时,缓圆点的脱轨系数最大,缓中点1的数值最小;当摩擦因数为0.30～0.50时,圆缓点的脱轨系数最大,缓中点1的数值最小。

图6 不同摩擦因数下脱轨系数最大值变化图Fig.6 Variation diagram of the maximum derailmentcoefficient under different friction coefficients

表6 曲线不同位置脱轨系数最大值峰值情况Table 6 The peak situation of the maximum value ofthe derailment coefficient at differentpositions of the curve

4 小半径曲线不同位置摩擦因数优化

根据磨耗指数、表面疲劳指数和脱轨系数3种评价指标的计算结果,首先进行数据的标准化;然后采用熵权法进行数据分析;最后计算出各项指标随摩擦因数变化的信息熵值和信息熵冗余度,从而求得各项指标的权重,结果如表7所示。

表7 各项评价指标权重系数Table 7 Weight coefficient of each evaluation index

由表7可知:各项评价指标的权重系数相差不大,其中磨耗指数的权重最大,表面疲劳指数的权重次之,脱轨系数的权重最小。根据表7的计算结果以及式(9)得到不同摩擦因数下各个位置的综合评分。综合得分越低,综合性能越好,对应的摩擦因数越理想,结果见图7。

图7 曲线不同位置处的综合得分Fig.7 Comprehensive score at differentpositions of the curve

由图7可知:直线点和曲中点的综合得分随着摩擦因数的增大均呈现出逐渐增大的趋势,其余各点综合得分的变化规律为先增大再减小;当摩擦因数一定时,缓圆点的综合得分最高,圆缓点次之,说明在小半径曲线下,需要对这两个位置进行适当润滑,以降低各项指标,提高车轮寿命和曲线安全性;直线点的综合得分最低,缓中点1的得分高于前者,但小于曲线其他位置的综合得分。

计算得到曲线各位置综合得分的平均值,规定低于该值的摩擦因数区间为该点的最佳摩擦因数区间;规定曲线不同位置综合得分最高与次高所对应的摩擦因数区间为该位置的危险摩擦因数区间。曲线不同位置的摩擦因数优化区间如表8所示。由表8可知:直线点与缓中点1的最佳摩擦因数为0.10～0.50,其范围较广，说明这两个点不需要轮轨润滑,曲中点的摩擦因数优化区间为0.10～0.30,缓中点2的摩擦因数优化区间为0.10～0.25,缓圆点和圆缓点的摩擦因数优化区间为0.10～0.20,其范围较窄，在小半径曲线对缓和曲线和圆曲线的连接处进行额外润滑可达到最佳摩擦因数,因此需要对小半径曲线不同位置进行不同的润滑控制,以较小的成本带来更好的防磨耗与疲劳性能;直线点和曲中点的危险摩擦因数区间为0.45～0.50,缓中点1的危险摩擦因数区间为0.30～0.35,缓圆点和圆缓点的危险摩擦因数区间为0.40～0.45,缓中点2的危险摩擦因数区间为0.35～0.40。

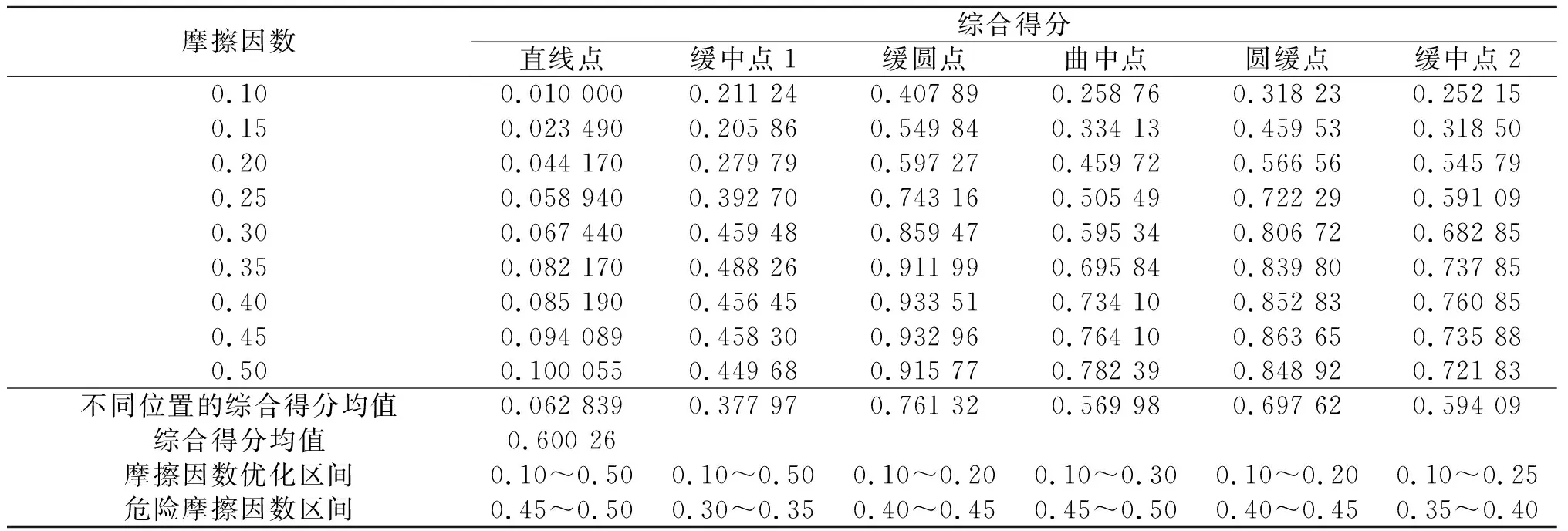
表8 曲线不同位置的摩擦因数优化区间Table 8 Optimal interval of friction coefficient at different positions of the curve

5 结 论

通过建立实际地铁车辆-轨道耦合动力学模型,研究了小半径曲线不同位置处的磨耗指数、表面疲劳指数和脱轨系数随摩擦因数的变化规律,通过熵权法分析得到了曲线不同位置的最佳摩擦因数区间和危险摩擦因数区间,得到以下结论:1) 地铁车辆在缓圆点和圆缓点处的磨耗指数、表面疲劳指数和脱轨系数等指标均明显比其他位置更大,因此在地铁小半径曲线的维护时要格外关注这两个位置;2) 综合考虑磨耗性能、滚动接触疲劳特性和曲线安全性,曲线各个位置的最佳摩擦因数区间和危险摩擦因数区间不同,其中缓圆点和圆缓点的最佳摩擦因数区间为0.10～0.20,危险摩擦因数区间为0.40～0.45,缓中点2的最佳摩擦因数区间为0.10～0.25,危险摩擦因数区间为0.35～0.40,曲中点的最佳摩擦因数区间为0.10～0.30,危险摩擦因数区间为0.45～0.50,缓中点1和直线点的最佳摩擦因数区间较广为0.10～0.50。以上结果可为地铁轮轨润滑提供技术支持,在地铁车辆实际运行过程中,可以通过改变润滑剂的涂抹量使得同一曲线不同位置的摩擦因数均在最佳区间内,以减轻车轮磨耗,减少疲劳裂纹的萌生,改善车辆安全性能,减少运营成本。