基于CNN-Seq2seq的河道水位区间预测方法

孙英军,唐为昊,王 成 ,李英德

(1.浙江省水文管理中心,浙江 杭州 310009;2.浙江工业大学 机械工程学院,浙江 杭州 310023)

河流重要水文站点的水位预测在水资源调控方面起着重要作用。水文预测模型在结构上可大体分为确定性模型、黑箱模型和概念性模型[1]。确定性模型以实际物理过程为基础,用物理理论描述水文系统。以SWAM模型[2]和IHDM模型[3]为代表的分布式流域水文模型是应用较为广泛的确定性模型。黑箱模型是一种由水文数据驱动的预测模型,将水文系统内部过程归结为统计关系,以非线性函数拟合模型的输入输出关系,常用于缺乏具体产汇流背景资料的水文预测。单位过程线[4]、支持向量机[5]和BP神经网络[6]都属于黑箱模型。概念性模型介于确定性模型和黑箱模型之间,是一种具有一定物理意义但在某些方面设置参数对水文物理过程进行简化的预测模型。常见的概念性模型有ARNO模型[7]和赵人俊等[8]提出的新安江模型。确定性模型和概念性模型都需要所研究流域具体的水文物理过程资料,例如应用新安江模型需要完成蒸发能力折算系数等14项参数的率定[9-10]。虽然一些学者将搜索算法应用于参数率定,并取得了一定成果,但是就我国广泛分布的水系而言,考察流域的水文物理过程资料是一项成本较高的工作,且一些流域的水文测量数据无法满足构建确定或概念性模型的输入数据需求,因此无法构建相关预测模型。

黑箱模型作为一种统计方法,预测过程不依赖于流域的物理过程基础,是一种相对通用的水文预测模型。以往的黑箱模型常采用一些较为简单的统计学习方法,例如以BP神经网络为代表的机器学习模型。这些方法将水文数据中隐含的物理过程用统计关系表达,虽然在学习数据内拟合效果良好,但是在外延预测过程中存在模型泛化能力不足等问题,使得预测效果大幅下降。近年来在机器学习基础上发展而来的深度学习一定程度上解决了过拟合等问题,提升了泛化性能,在计算机视觉、自然语言理解和复杂过程预测等诸多场景展现了其强大的性能。水文预测领域亦有大量采用深度学习方法的相关研究,例如衣学军等[11]将小波非线性自回归网络应用于渭河流域水位站点的径流量预测;Zhao等[12]为了解决高泥沙含量的河道水位不平衡预测问题,提出了一种混合机器学习框架;Xiang等[13]将Seq2Seq模型应用于降雨量-径流量关系回归问题中;纪国良等[14]将循环神经网络应用于水库水位预测,预测效果优于水动力学模型;倪汉杰等[15]将小波分析与长短期记忆网络相结合,设计了一种航道水位智能预测模型。上述研究提出的黑箱模型均包含由Hochreiter等[16]设计的长短期记忆网络(LSTM)。LSTM独特的“门”结构使其能自适应地选择数据中需要被“遗忘”以及“记忆”的部分,选择性保留数据的循环结构使其成为处理时间序列问题的首选深度学习模型之一。虽然大量研究验证了LSTM提取时序特征的能力,但其受限于循环单元结构而难以处理空间特征(在各个循环步输入的协变量)。例如水位预测任务中LSTM可很好地利用水位变化的时序特征,却无法有效利用由降雨量组成的空间特征。为解决上述问题,设计了一种基于LSTM和一维卷积神经网络(CNN)的混合神经网络——卷积-序列到序列(Convolutional neural networks-Sequence to sequence,CNN-Seq2seq)黑箱水文预测模型。在流域物理过程资料未知的背景下,将设计的混合神经网络应用于西苕溪流域水位预测任务中。模型在测试数据集上的预测准确性相较于其他黑箱预测模型更优,证明了所设计的混合神经网络能有效改进LSTM在提取空间特征上存在的缺陷,提高了河道水位预测的准确性。

1 研究流域与数据

1.1 研究流域

研究预测对象为西苕溪流域内河道水位。西苕溪流域如图1所示。该流域位于浙江省北部安吉县境内,东经119°14～119°45,北纬30°22～30°45,是太湖的主要支流之一。流域面积约2 200 km2,平均海拔高度266 m。作为该流域内的主要河流,西苕溪自西南山区流向东北部汇入太湖。该地区属于亚热带季风气候,年平均温度12.2～15.6 ℃,年平均降水量约1 500 mm,超过70%的降雨发生在丰水期(4—10月)。为了控制洪水同时兼具水资源调配等功能,分别于1958年和1972年在西苕溪上游修建了老石坎和赋石两座大型水库。

图1 西苕溪流域地图Fig.1 Map of the Xitiaoxi watershed

1.2 水文数据

西苕溪流域内建有30个雨量测量站点、4个河道水位测量站点和2个水库水位测量站点。采集了上述水文测量站点2014—2019年逐5 min的数据记录,赋石、老石坎两座水库在此期间逐1 h的泄洪记录。对雨量数据按照小时累计求和,水位数据逐小时求平均,共获得46 451 h的水文数据记录。按照水利部门相关预测需求,预测模型对“杨家埠”“梅溪”“横塘村”“港口”4个水位测量站点的水位高度进行预见期为12 h逐小时的预测。

2 主要方法

2.1 序列到序列结构

长短期记忆网络(Long short-term memory,LSTM)是一种为了解决长时依赖问题而改进的循环神经网络,通过在循环单元中加入帮助神经网络选择“遗忘”不重要信息的遗忘门、增强对重要信息“记忆”的记忆门和使神经网络能综合考虑输入信息并生成输出张量的输出门。长短期记忆网络结构如图2所示。网络结构中的xt表示在时间点t输入网络中的特征向量;ht表示在时间点t的网络计算输出;Ct被称为循环单元的隐含状态,其中包含了在时间点t的网络长时记忆信息。每个时间点中,LSTM的循环单元都需要更新6个参数,具体计算过程为

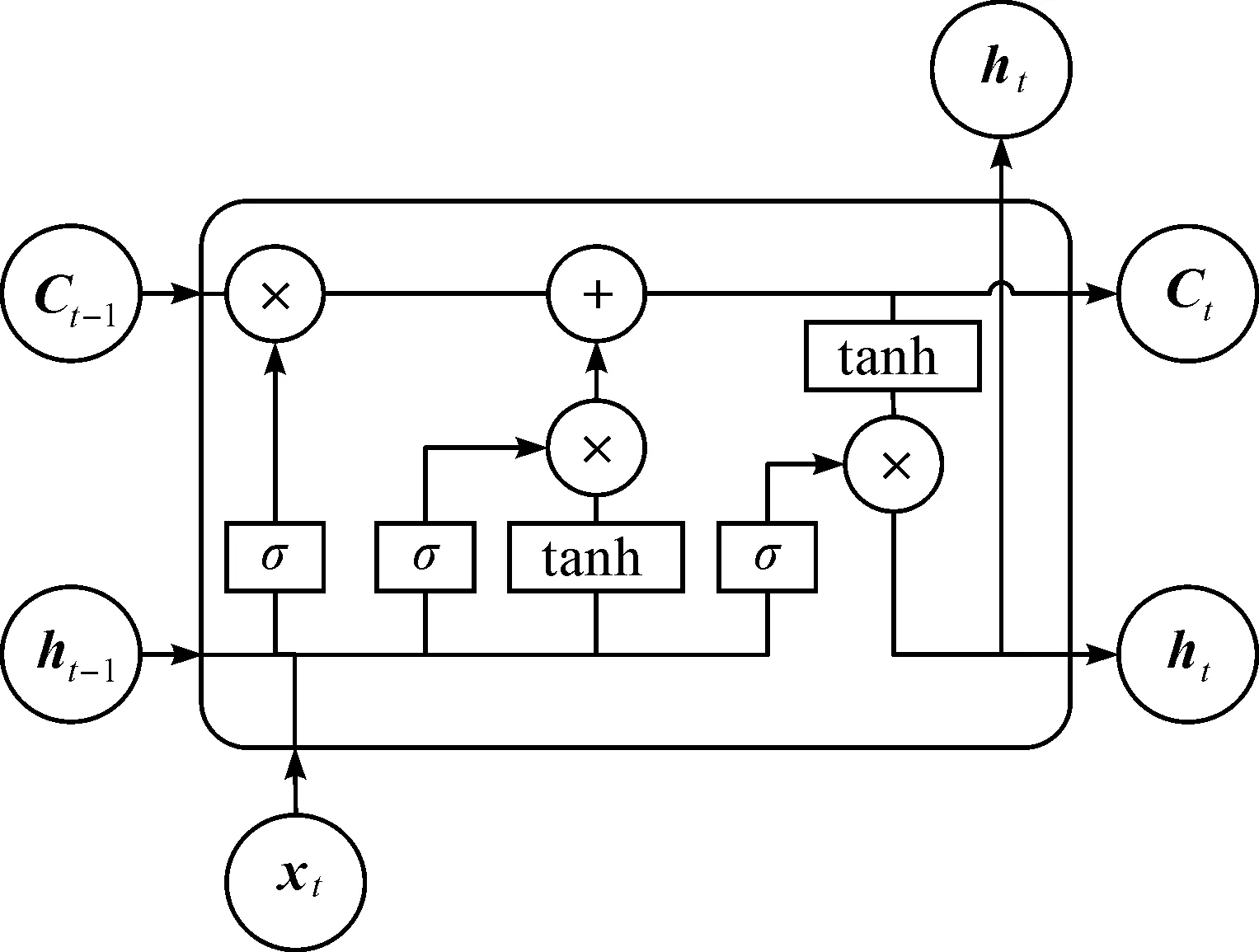
图2 长短期记忆网络循环单元结构Fig.2 Basic long short-term memory networkrecursive unit structure

ft=σ(Wf·[ht-1,xt]+bf)

(1)

it=σ(Wi·[ht-1,xt]+bi)

(2)

C′t=tanh(WC·[ht-1,xt]+bC)

(3)

Ct=ft×Ct-1+it×C′t

(4)

ot=σ(Wo·[ht-1,xt]+bo)

(5)

ht=ot×tanh(Ct)

(6)

式中:σ(·),tanh(·)分别表示Sigmoid和tanh激活函数,其计算式为

(7)

(8)

LSTM虽然能解决长时依赖问题,但是仍然存在几个缺陷:1) 随着预测时段时间步的增加,预测误差大幅上升;2) 无法考虑降雨预测数据等预测时段的协变量信息;3) 训练过程收敛速度较慢。Cho等[17]提出了一种能有效解决上述问题的网络结构,该结构被称为序列到序列(Seq2seq)或编码器解码器(Encoder-Decoder)。Seq2seq结构包含两组独立的LSTM循环单元:一组循环单元将历史时段的时序特征压缩为隐含特征(如图3中的LSTM循环单元1);另一组循环单元根据压缩后的隐含特征和预测时段的协变量特征(如果存在)循环输出最终预测结果(如图3中的LSTM循环单元2)。Salinas等[18]在Seq2seq的基础上设计了DeepAR概率预测模型,该模型在训练过程中加入“teacher forcing”策略,使训练过程的收敛速度有所加快。包含“teacher forcing”策略的Seq2seq模型训练过程和预测过程如图3所示。

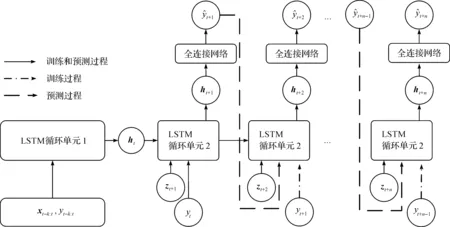
图3 包含“teacher forcing”策略的Seq2seq模型训练和预测过程Fig.3 Seq2seq model training and prediction process with teacher forcing strategy

2.2 一维卷积神经网络

长短期记忆网络虽然在时序数据特征提取上展现了强大的性能,但是在空间多特征学习上受到了内部结构的制约。卷积神经网络(Convolutional neural networks,CNN)因其空间特征提取能力和相对较少的模型参数,被广泛应用于计算机视觉领域。根据卷积核的不同可将卷积神经网络分为一维、二维和三维卷积,其中一维卷积网络(1D-CNN)常被用于提取时序数据的空间特征。

一维卷积网络采用数个不同卷积核以一定步长在输入数据的时间维上滑动与输入数据相乘来提取数据的隐含特征。相较于全连接网络,一维卷积网络的卷积计算方式具有更少的参数,并能更好地提取出局部特征。卷积运算过程为

x′=relu(Wk*x+bk)

(9)

式中:*表示卷积运算;Wk表示卷积核权重矩阵;bk表示卷积偏置项;relu(x)=max{x,0}表示非线性激活函数。

2.3 CNN-Seq2seq模型

将一维卷积网络和Seq2seq模型相融合,提出了一种时间序列预测模型——卷积-序列到序列模型(Convolutional neural networks-Sequence to sequence,CNN-Seq2seq)。结合水位预测期长、特征多的特点,将长短期记忆网络和卷积神经网络的优势相结合,由一维卷积网络提取以多站点的降雨量数据为代表的空间特征,再由Seq2seq模型提取水位数据变化情况的时序特征,最后由全连接网络根据所提取到的隐含特征计算得出所需预测信息。

由于随机因素的存在,水位预测总是存在预测误差,因此相较于具体水位高度的预测,预测未来水位高度的置信区间更具现实意义,相关水利决策可以根据预测水位置信区间的上下界作出相应调整。按照预测需求,所设计的模型输出未来12 h内逐小时河道水位的10%,50%和90%分位数。预测模型结构如图4所示。

图4 CNN-Seq2seq模型结构Fig.4 Model structure of CNN-Seq2seq

2.4 损失函数与评价指标

深度学习模型的迭代优化依赖于预测损失所提供的梯度信息,合理选择损失函数可以提升预测准确性,增强模型泛化能力。预测损失通常是无量纲的,因此需要更加符合直觉的评价指标以评价模型的实际预测效果。区间预测包含两种思路:概率回归假定被预测对象服从某种概率分布,构建的预测模型对该分布的参数进行预测,并由预测得到的分布参数计算得出希望获得的概率分布分位数,该方法一般使用极大似然估计作为损失函数;分位数回归不需要假定被预测对象的概率分布,直接对有限个分位数进行预测,这种方法使用分位数损失作为损失函数。水文预测具有高度不确定性和不平稳性,难以假定所服从的概率分布,因此选择分位数回归进行预测,分位数损失函数为

(10)

式中:Ω表示包含M个训练样本的集合;Q表示输出分位数的集合(按照实际需求,输出Q={0.1,0.5,0.9});yt,j表示样本yt在预见期j的水位高度;n表示预见期长度;(x)+=max(0,x)。

在进行模型评价时,使用标准化分位数损失(q-risk)对模型在验证集和测试集上的性能进行评估[23-24],q-risk代表对分位数“q”的计算结果,例如0.1-risk表示对10%分位数的标准化分位数损失。具体计算式为

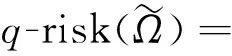
(11)

使用区间覆盖率(IC)验证预测置信区间的合理性,置信区间由所预测得到的0.1和0.9分位数决定。区间覆盖率越接近于两分位数数值之差越优。区间覆盖率偏大则说明预测置信区间过宽,覆盖率偏小则说明预测置信区间过窄。区间覆盖率计算式为

(12)

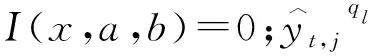
使用纳什效率系数(NSE)、洪峰预报误差(QL)和洪峰出现时间误差(QT)对洪水过程预测效果进行辅助评价,纳什效率系数计算式为

(13)

洪峰水位误差计算式为

(14)

洪峰出现时间误差计算式为

(15)

洪峰水位误差反映了洪水预测峰值和实测峰值的差距,洪峰出现时间误差反映了洪水预测峰值出现时刻和实测峰值出现时刻的误差。QL和QT在数值上越接近于0则模型对洪峰水位大小和出现时间预测越准确。

3 对比实验

3.1 数据预处理

研究流域的水文数据记录包含大量异常值和空缺值,要使用这些数据进行模型训练需要剔除异常值并对空缺值进行填补,无法填补的样本则弃而不用。剔除异常数据,对水位数据按小时求均值、对雨量数据按小时求均值,若水位数据被求均值的区间包含但不全为空缺值,则对剩余数据求均值,考虑到短时强降雨等情况的存在,雨量数据若被求和的区间包含空缺值,则将求和结果置为空缺。一些水位站点在使用时存在基准调整的过程,调整前后的测量数据存在整体偏差,选择最长时间未进行基准调整的数据作为基准,其他时间段的数据按照此基准进行数值调整。对空缺间隔小于5 h的水位数据使用线性插值补全。

水位、雨量和放水量数据相差较大,对数据进行标准化处理可避免模型过度考虑某些数值上较大的特征,标准化过程为

(16)

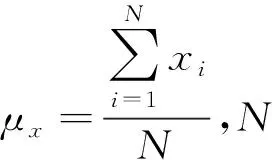
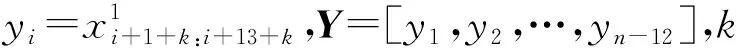
按照70%,15%和15%的比例将输入数据划分为训练集、验证集和测试集,则xtrain=[h1:0.7n,f1:0.7n,y1:0.7n],xvalidate=[h0.7n:0.85n,f0.7n:0.85n,y0.7n:0.85n],xtest=[h0.85n:n-12,f0.85n:n-12,y0.85n:n-12]。xtrain表示训练集用于训练构建的预测模型;xvalidate表示验证集用于验证训练好的模型的泛化能力并根据验证结果进行模型调优;xtest表示测试集用于对比不同模型的泛化能力。

3.2 超参数选择

要获得性能优异的预测模型,构建理想的模型结构与选择合适的模型超参数同样重要。对于构建的深度学习算法A,其根本目的在于找到一个函数f使得给定损失函数的损失L(x;f)最小,x采样自预测数据的真实分布Gx。A的学习过程可以看作将真实分布Gx的有限采样xtrain映射为预测模型f。对于参数化的算法A,总是存在影响预测模型性能的超参数组Λ,算法A选用超参数λ∈Λ在数据集xtrain上训练得到预测模型f的过程可以表示为f=Aλ(xtrain)。例如对于一个全连接神经网络,需要选择调整的超参数包括网络层数、每层网络神经网络的神经元数量、神经元选择的激活函数以及是否使用参数正则项、正则项的权重大小等。超参数优化问题可以表示为

(17)

对式(17)的优化是十分困难的:一方面深度学习模型的模型训练时间较长,意味着每次计算L(x;Aλ(xtrain))都需要较大的开销,因此在搜索空间较大时不可能完成对所有超参数组合空间Λ的遍历搜索;另一方面L(x;Aλ(xtrain))不存在导数信息,因此无法使用梯度下降等方法进行求解。Bergstra等[25]通过大量实验证明了随机搜索方法在相同时间开销中对超参数优化的搜索效率高于传统的网格搜索或人工调整搜索。随机搜索即在Λ中随机选择λ并评估L,在给定时间内重复此过程并记录最小的L和对应的超参数组合。

采用随机搜索方法对模型超参数进行寻优,以q-risk作为损失函数计算L(xvalidate;Aλ(xtrain))评估超参数组合。构建的CNN-Seq2seq模型可选的超参数包括:1) 历史数据长度k(12,24,48,60,72);2) Dropout比例(0.1,0.2,0.3,0.4,0.5,0.6);3) Batchsize大小(32,64,128,256);4) 优化器学习率(0.000 1,0.001,0.01);5) 最大梯度裁剪(0.01,0.1,1.0,100.0);6) LSTM网络神经元数量(16,32,64,128);7) LSTM网络层数(1,3,6);8) CNN网络卷积核数(8,16,32,64);9) CNN网络层数(4,8,16,32);10) 训练迭代数(10,25,50,75,100,150,200)。

3.3 对比模型

为了验证构建的CNN-Seq2seq深度学习预测模型在水位区间预测任务上相较于其他黑箱模型的优势,选择4种常用的预测模型、1种预测基准(Baseline)以及仅使用Seq2seq结构的预测模型进行比较。1) ARIMA:经典的统计预测方法,被广泛应用于自回归预测任务,采用Hyndman-Khandakar算法求解最优模型参数;2) NN:全连接神经网络凭借其简单的网络结构和灵活的输入输出关系被应用于多种预测任务,使用随机搜索进行隐含层层数和隐含神经元数量寻优;3) LSTM:仅使用长短期记忆网络提取时间序列的隐含特征,由全连接网络根据提取出的特征输出预测结果[31];4) DeepAR:采用Seq2seq结构、“teacher forcing”训练策略的概率预测方法,是应用较为广泛的深度学习预测模型之一;5) Seq2seq:在构建的CNN-Seq2seq模型中去除一维卷积结构,用于验证一维卷积提取输入数据特征的能力,LSTM,DeepAR和Seq2seq模型与构建的CNN-Seq2seq模型均具有类似的网络拓扑结构,因此上述4种模型在隐含层层数和神经元数量上保持一致,由CNN-Seq2seq模型的超参数寻优结果确定;6) Baseline:不采用任何预测模型,以预测发生时刻的水位高度作为预测结果。Baseline的预测性能是预测模型性能的下限,上述模型的预测效果不应差于Baseline。所选用的对比模型具有相同的输入输出关系,均以历史m小时内的水位高度为输入,输出未来n小时内的水位预测结果。然而这些模型在能否考虑协变量信息、时序信息以及进行不确定性预测(分位数或概率预测)上有所区别(表1)。图5反映了CNN-Seq2seq模型和Baseline对“梅溪”站点2019年6月20日19时至次日7时水位的预测效果,图5中短虚线为Baseline,长虚线和阴影部分为CNN-Seq2seq模型的预测结果。预测事件发生在图5中的第48 h。

表1 对比模型所考虑的信息Table 1 Information considered in the comparison model

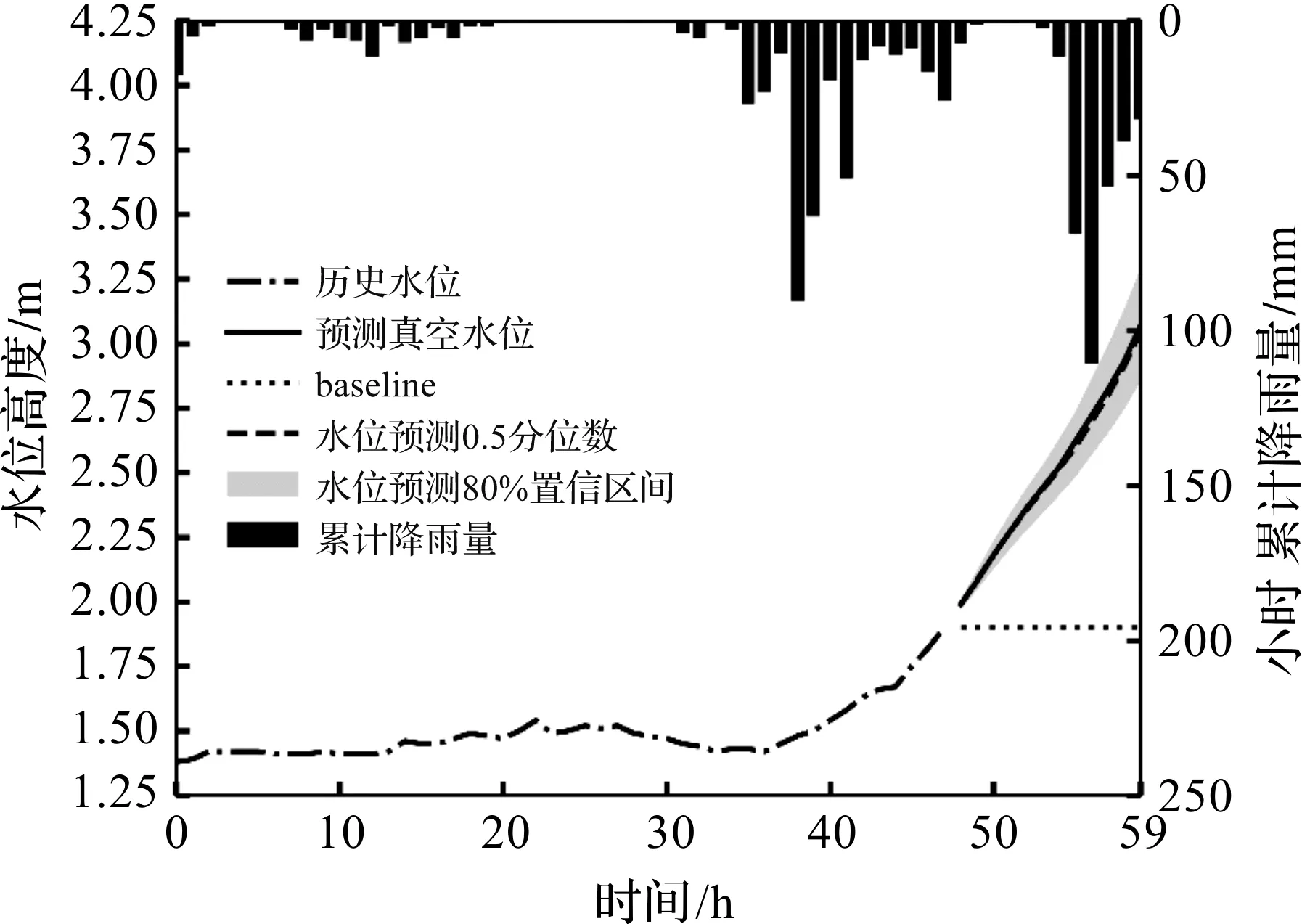
图5 Baseline预测示意图Fig.5 Prediction baseline schematic

结合所选择的模型,整体实验过程包括4步:1) 整理水文数据记录,对数据进行清洗和填补;2) 将水文数据以滑动窗口的方式构造为数据样本,并将数据样本划分为训练集、验证集和测试集;3) 使用训练集完成各个模型的训练,在验证集上调优各个模型的超参数,考虑到深度学习训练过程的随机性,每个超参数组合对应的模型重复训练5次,取其在验证集上的平均损失作为评价指标,完成50次搜索后选择在验证集上损失最小的模型作为最终训练结果;4) 根据评价指标,对比各个模型在测试集上的预测效果。

4 实验结果与分析

能否准确预测洪水过程是考察水位预测结果可靠性的关键因素。相较于非洪水过程,洪水水文过程具有不确定性高、非平稳和无周期性等特点,因此对其进行准确预测是相对困难的。为了检验模型水位预测结果的可靠性,在测试集上分别对含有洪水和非洪水的整体水文过程和仅含洪水过程的数据样本进行水位预测准确性评估。

对整体水文过程预测结果的评估可以反映模型区分洪水和非洪水水文特征的能力,验证模型是否会将非洪水过程预测为洪水过程。选择标准化分位数损失作为整体水文过程预测结果的评估指标。与模型所输出的10%,50%和90%水位分位数预测保持一致,评估指标包括0.1-risk,0.5-risk和0.9-risk。0.1-risk和0.9-risk两项指标检验了模型所预测的区间上界和下界的准确性,在这两项指标上较优的模型能给出更合理的80%水位置信区间预测,0.5-risk反映了模型在水位真值预测上的相对偏差。

经过超参数优化后的模型在测试集上对整体水文过程的预测结果如表2所示。表2中粗体为各模型间准确性最高的预测结果;“平均”列表示该模型在4个水位预测任务中的平均表现;“p”列表示前一列平均值减去最优结果的差与最优结果的比值,反映了与最优结果的相对差距。LSTM,NN和Baseline只能完成河道水位的点预测(输出50%分位数),因此在0.1-risk和0.9-risk两项指标上无数据。

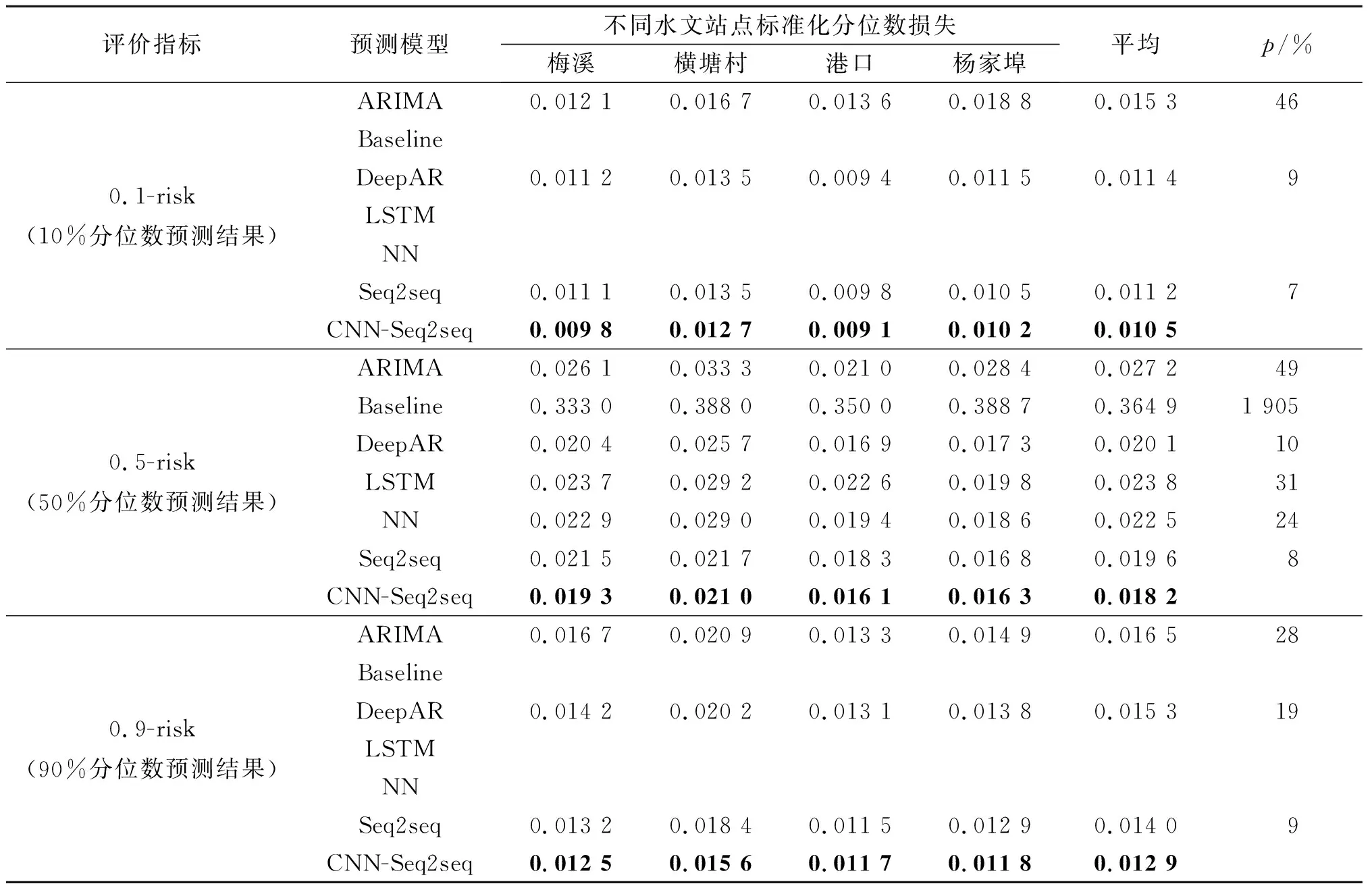
表2 标准化分位数损失(整体水文过程)Table 2 Standardized quantile loss (Overall hydrological process)

整体水文过程的预测准确性评估结果表明:构建的CNN-Seq2seq预测模型除了在“港口”站点90%分位数的预测准确性上略差于Seq2seq模型外(劣化1.71%),其余站点的准确性均优于其他模型(在0.1-risk上优于其他模型7%～46%,在0.5-risk上优于其他模型8%～49%,在0.9-risk上优于其他模型9%～28%)。

采用区间覆盖率评估水位预测置信区间的预测准确性。预测模型输出水位预测的0.1和0.9分位数,因此区间覆盖率应接近于0.80。模型在测试数据集上的区间覆盖率统计结果如表3所示。结果显示:ARIMA和Seq2seq模型的预测置信区间过窄,而DeepAR模型的置信区间过宽,CNN-Seq2seq模型的区间覆盖率最接近于要求的80%置信区间。

表3 区间覆盖率(整体水文过程)Table 3 Interval coverage (Overall hydrologic process)

为了评估洪水过程的水位预测准确性,需在测试数据集中划分洪水过程和非洪水过程。测试数据集包含了2018年10月—2019年8月的河道水位数据,其中包括6次洪水过程,结果如图6所示,黑框中为各个站点标记的洪水过程。

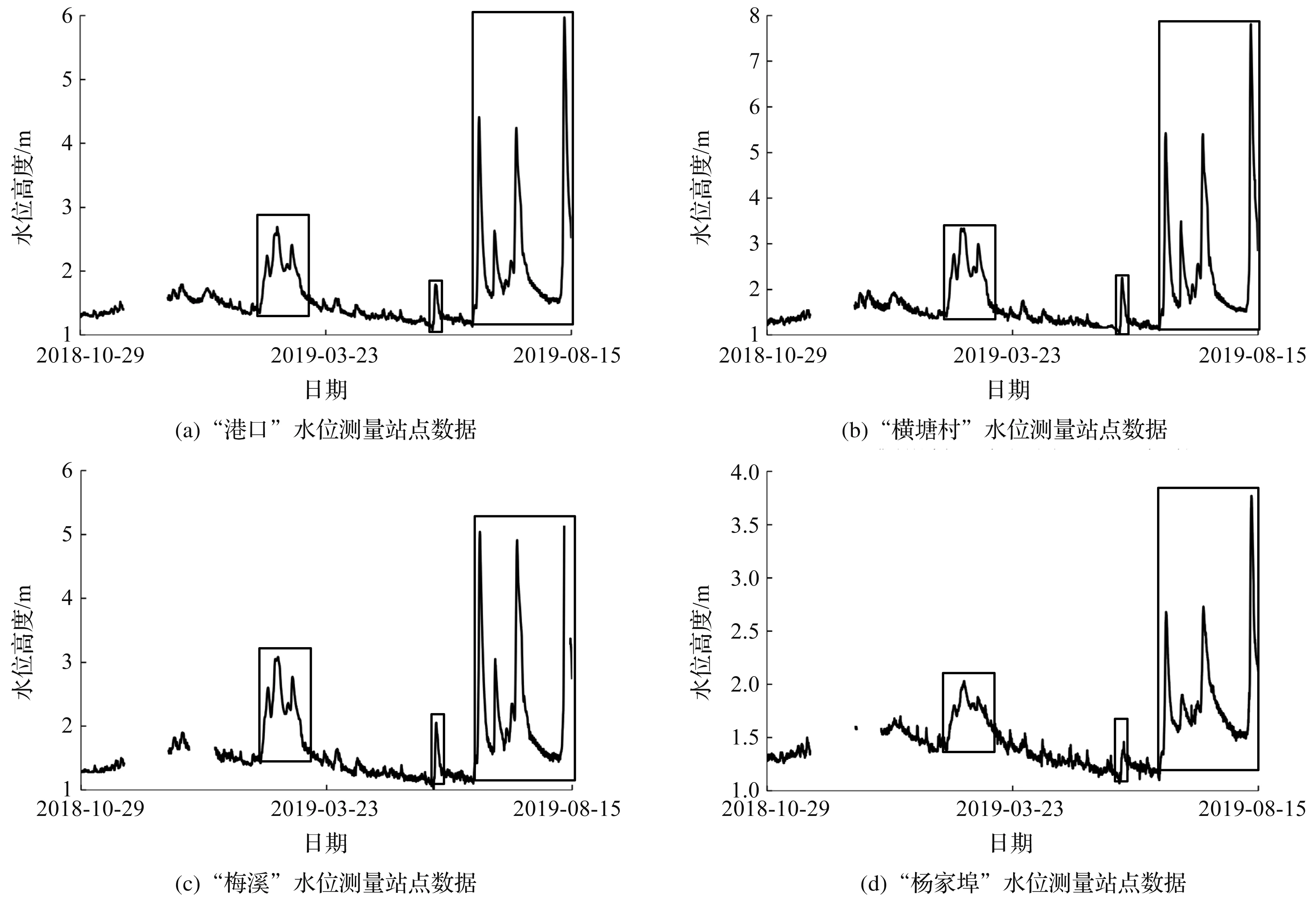
图6 测试数据集中的洪水时间段Fig.6 Flood period in the test dataset

洪水过程所在时间段分别为2019年2月12日18时—2019年3月10日0时,编号“2019-02-12”;2019年5月26日6时—2019年5月30日12时,编号“2019-05-26”;2019年6月19日18时—2019年6月27日18时,编号“2019-06-19”;2019年6月30日0时—2019年7月7日0时,编号“2019-06-30”;2019年7月9日0时—2019年7月21日0时,编号“2019-07-09”。开始于2019年8月10日的洪水过程因缺少水位、雨量等数据,不参与评估。

NN,LSTM和Baseline无法进行区间预测,表2的评估结果中CNN-Seq2seq,Seq2seq和DeepAR 3种模型的预测准确性相近,而ARIMA模型的准确性较差。为了兼顾水位的区间预测功能和水位点预测具有较高的准确性,排除在整体水文过程中预测性能不佳的NN,LSTM,ARIMA和Baseline。采用纳什效率系数、洪峰预报误差和洪峰出现时间误差3项指标,对CNN-Seq2seq,Seq2seq和DeepAR模型在上述洪水过程预见期为6 h和12 h的预测准确性进行评估,结果如表4～6所示。

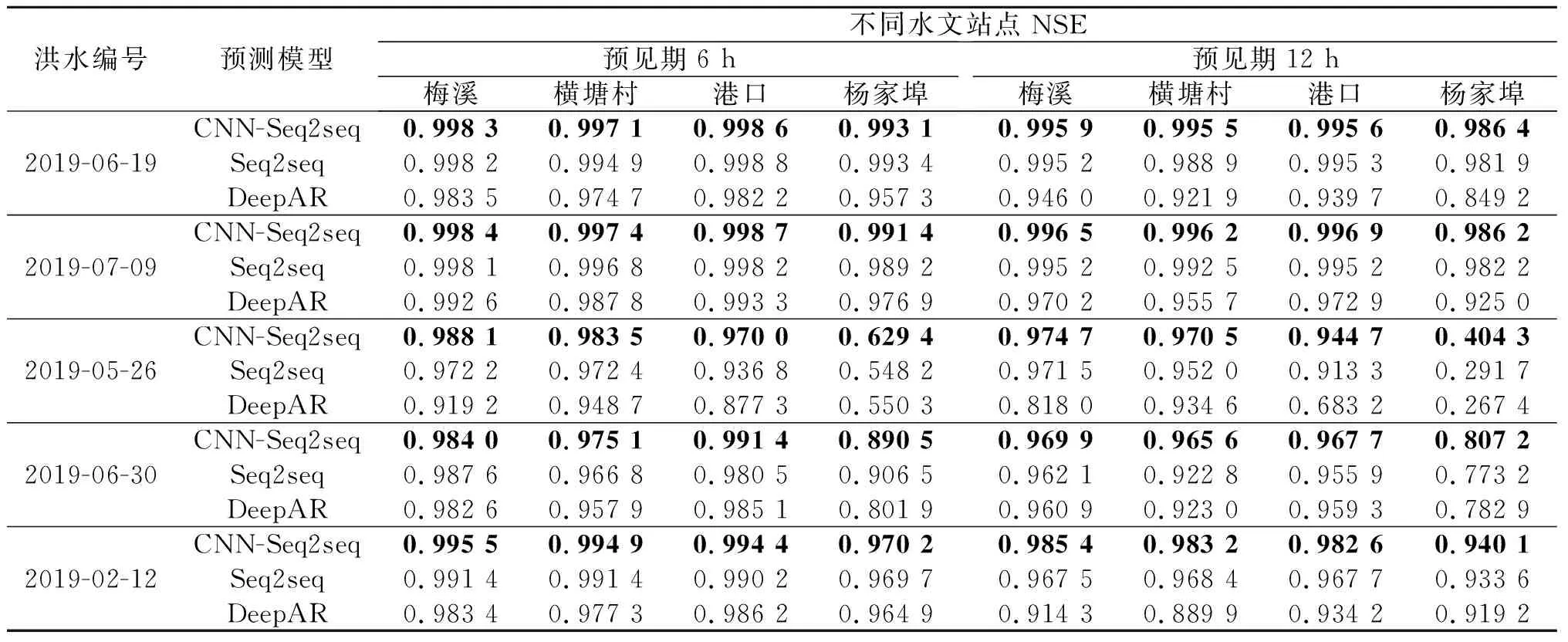
表4 纳什效率系数(洪水时间段,NSE)Table 4 Nash efficiency coefficient (flood period, NSE)

表5 实测洪峰出现时间误差(QT)Table 5 The actual measurement of the flood peak appeared time error (QT)

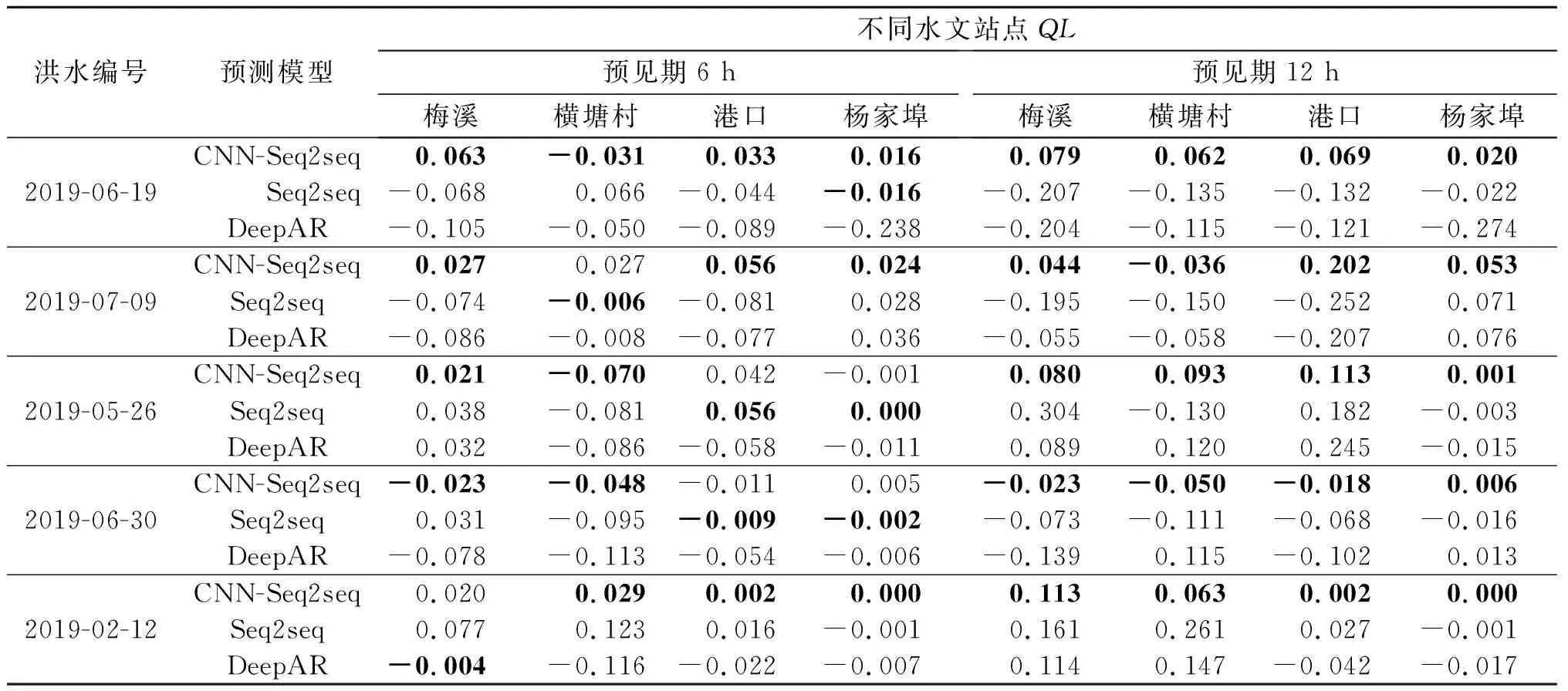
表6 实测洪峰水位高度误差(QL)Table 6 The actual measurement of the flood peak level error (QL)

对洪水过程的预测准确性评估显示:CNN-Seq2seq模型在绝大部分洪水的评估指标上优于其他模型,在未达最优的指标上与最优指标仍保持较小的差距。CNN-Seq2seq模型除“杨家埠”站点“2019-05-26”号洪水外的所有洪水过程均能做到在预见期内对洪峰到来进行准确预测。3个模型关于“杨家埠”站点“2019-05-26”号洪水的预测结果均出现了明显下降。CNN-Seq2seq模型预见期6,12 h的水位预测纳什效率系数分别下降至0.6,0.4,峰现时间误差分别达到了5,11 h。经过对数据集的检查,发现“杨家埠”站点洪水中的洪峰相较于其他站点在时间上有明显偏移,推测该站点所记录数据存在异常,致使水位变化情况无法被准确预测。

对上述评估结果中各水文站点的所有洪水过程求平均,结果如表7所示。

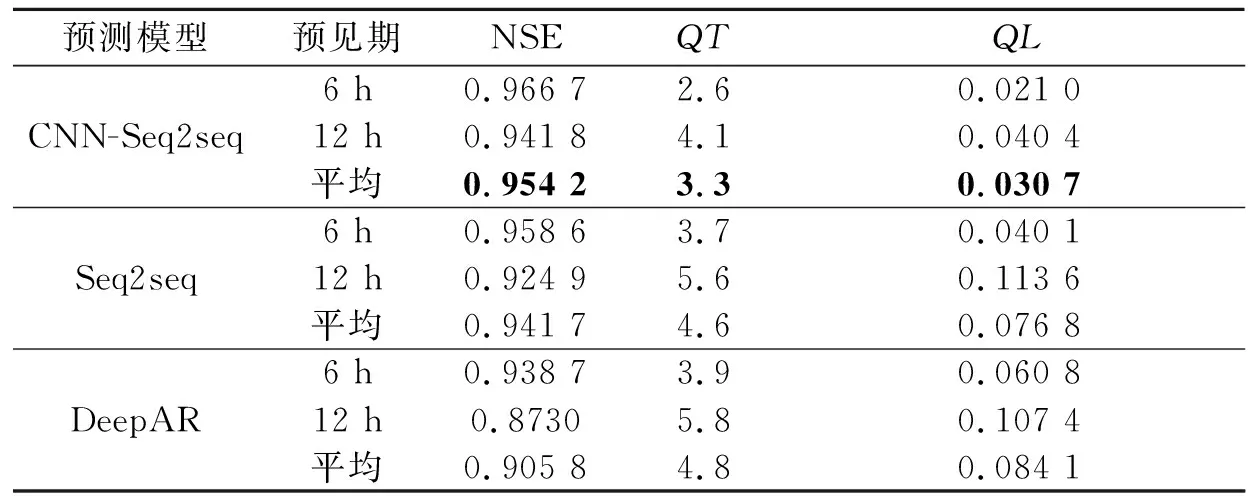
表7 洪水过程平均评估指标Table 7 Flood process average assessment indexes

从洪水过程预测结果的平均指标来看,构建的CNN-Seq2seq模型是所有模型中预测精度最高的。CNN-Seq2seq模型在所有指标上均优于其他两个模型,表明构建的CNN-Seq2seq模型在洪水预测上具有更好的预测精度。

选择测试数据集中最后一场数据记录完整的洪水过程绘制预测效果图。CNN-Seq2seq,Seq2seq和DeepAR模型对编号“2019-07-09”的洪水以预见期6,12 h进行预测的效果如图7,8所示。

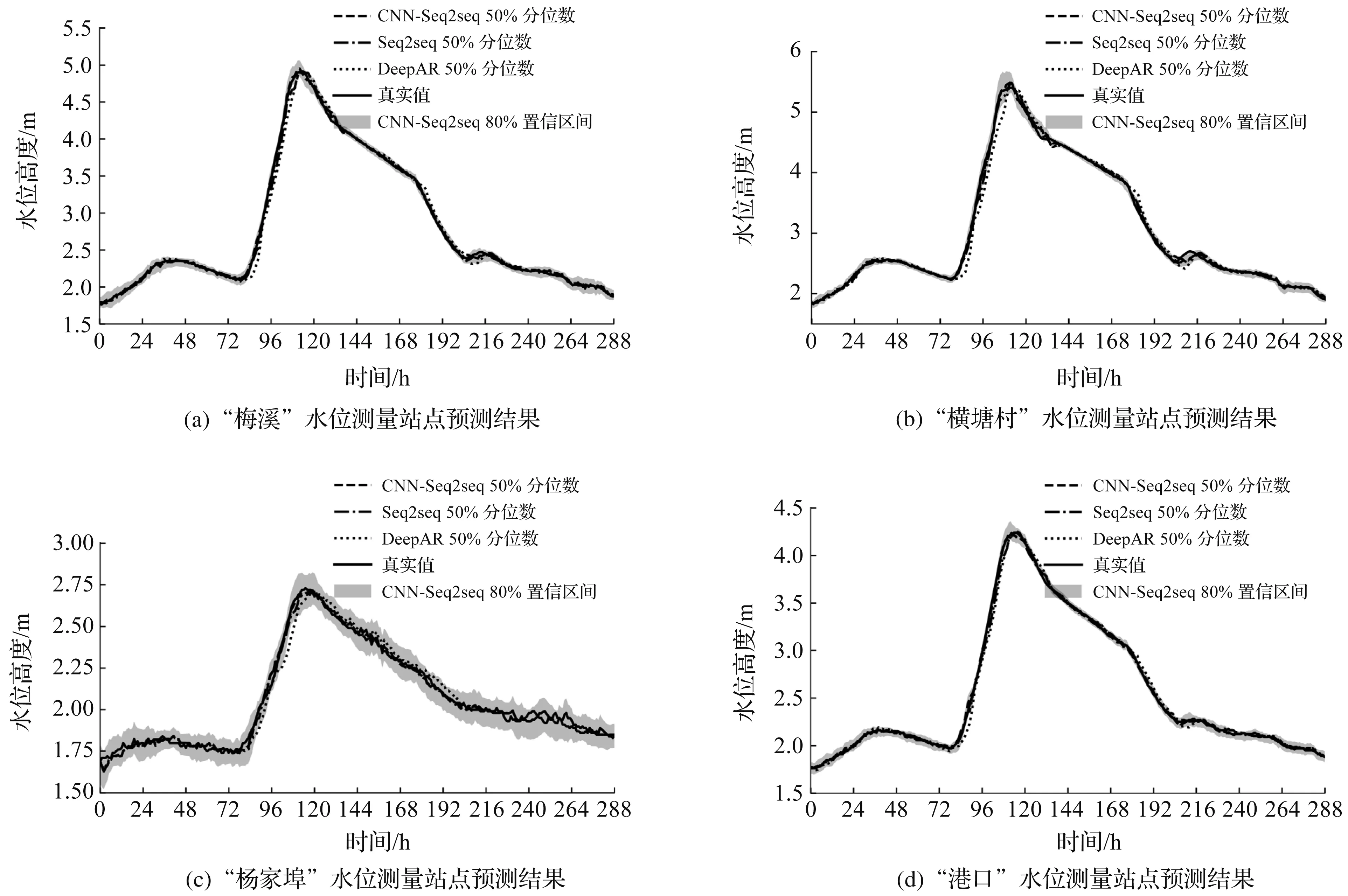
图7 “2019-07-09”号洪水6 h预见期预测效果Fig.7 Flood prediction effect of “2019-07-09” with 6-hour forecasting horizon

图8 “2019-07-09”号洪水12 h预见期预测效果Fig.8 Flood prediction effect of “2019-07-09” with 12-hour forecasting horizon

为了更清晰地反映各个模型在“2019-07-09”号洪水过程中水位高度点预测效果的差异,仅绘制CNN-Seq2seq模型的区间预测结果。CNN-Seq2seq和Seq2seq在该洪水过程中的水位高度点预测准确性上较为接近,而DeepAR的预测误差较大。例如在“杨家埠”站点12 h预见期第96 h的预测结果中,CNN-Seq2seq和Seq2seq模型的绝对预测误差接近于0 m,而DeepAR模型的绝对预测误差达到了0.4 m。

水文过程总是存在不确定性,因此无法对水位变化情况作出完全准确的预测。河道水位区间预测是对水位预测误差的补充,在水文状态不明确时(例如洪峰前后),模型倾向于输出范围更大的水位预测置信区间。虽然在一些情况下水位的预测值和真值会出现较大误差,但通过预测的置信区间仍能得到关于水位变化情况的估计。在防洪减灾等应用上可将预测置信区间的上界考虑为水位预测结果,以确保更为稳妥的决策方案。

5 结 论

为了实现缺乏水文流域物理过程资料的短时河道水位预测,设计了一种基于一维卷积网络和长短期记忆网络的河道水位实时预测模型CNN-Seq2seq。将历史水文数据记录作为预测模型的训练样本,采用“teacher forcing”策略完成对模型的训练,使模型能预测流域下游4个河道水位测量站点未来12 h内逐小时的10%,50%和90%河道水位分位数。对比ARIMA,DeepAR,LSTM,NN和Seq2seq模型的预测准确性,实验结果表明:CNN-Seq2seq不仅整体水文过程的预测精度优于其他模型,而且对洪水水位的预测同样具有较高精度,并优于其他模型。实验验证了CNN-Seq2seq模型在脱离产汇流机制的情况下仍能对短时河道水位变化过程作出较高精度的预测,经过合理设计的黑箱水文预测模型兼具通用性和预测可靠性。