高中数学解题教学中运用设问渗透数学学科核心素养的探究

摘 要：数学解题课是高中数学教师和学生普遍重视的一种课型。教师要合理借助设问，发展学生的数学思维，通过各种手段和途径，不断提高设问的质量和效率，从而赋予解题教学更多的活力，激发学生的学习兴趣，提高学生的解题能力。

关键词：高中数学;解题教学;设问;核心素养

中图分类号：G427                                文献标识码：A                                       文章编号：2097-1737（2022）21-0070-03

引  言

在新课程改革背景下，教师应创新教学模式，赋予解题教学更多的活力，在解题教学中运用设问，设计各类数学问题，引导学生积极思考，发展学生的数学思维，培养学生的数学学科核心素养。

一、在高中数学解题教学中运用设问渗透数学学科核心素养的案例分析

（一）设计“启发性”问题，提高学生的数学思维能力

例如，我国古代著名的数学专著《九章算术》里有这样一段叙述：“今有良马与驽马发长安至齐，骑去长安一千一百二十五里，良马初日行一百零三里，日增一十三里;驽马初日行九十七里，日减半里，良马先至齐，复还迎驽马，二马相逢，问几日相逢？”学生对此题的解答没有思路。此时，教师便可以给予学生相应提示，引导学生对问题进行解答。

“良马”每日行的里程构成以103为首项，13为公差的数列;“驽马”每日行的里程构成以97为首项，

-为公差的等差数列。当两马相逢时，两马共行驶了1125×2里，由此利用等差数列前n项和公式列方程求解。

设n日相逢，依题意得103n +×13 +

97n +×（-）= 1125×2，整理以后得n2 + 31n -360 = 0，解得n = 9（负值舍去）。

学生意识到这道题能够转化为等差数列问题时，便抓住了解题的关键，进而根据题目中提供的相关已知条件，求得答案[1]。

（二）设计“质疑性”问题，培养学生的分析理解能力

在新课程改革背景下，教师需要重新树立设问意识，懂得质疑的意义和价值，从而在课堂中提出更适合学生的问题，在潜移默化中培养学生的逻辑推理能力。

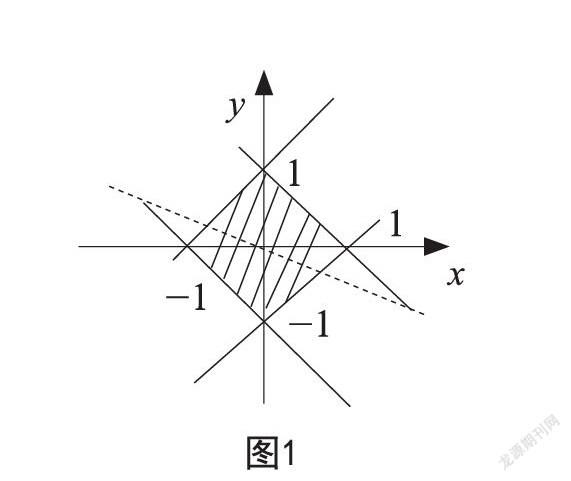
例如，设变量x，y滿足|x| + |y|≤1，则x + 2y的最大值和最小值分别为多少？

此题属于线性规划问题。在学生无从下手之时，教师需要进行适当点拨，提出相关问题，引导学生进行思考和分析，从而找出正确答案。例如，教师可以引导学生画出|x|+|y|≤1表示的平面区域。其中，x + y = 1，

x + y = -1，x - y = -1，x - y = 1，这四条直线的交点分别为（0，1），（0，-1），（1，0），（-1，0）。由图1可知，当目标函数过点（0，1）时，取得最大值，即x + 2y = 2;

过点（0，-1）时，取得最小值，即x + 2y = -2。经过这样的教学过程，教师能够更好地帮助学生理解相关数学知识，培养学生的核心素养，强化学生的学习效果[2]。

（三）设计“提升性”问题，提升学生的观察问题能力

例如，在△ABC中，内角A、B、C的对边长分别为a、b、c，已知a2 - c2 = 2b，且sinAcosC = 3cosAsinC，求b。

此题是对正弦定理和余弦定理的简单应用，学生先利用余弦定理，得出a2 - c2 = b2 - 2bccosA。

又因为a2 - c2 = 2b，b≠0，所以b = 2ccosA + 2。①

又因为sinAcosC = 3cosAsinC，

sinAcosC + cosAsinC = 4cosAsinC，

sin（A + C） = 4cosAsinC，

sinB = 4sinCcosA。

利用正弦定理，得出sinB = sinC，

所以b = 4ccosA。②

由①②，解得b = 4。

教学讲究的是循序渐进，教师应遵循由简入难的原则提出相关问题。教师需要多提出一些具有“提升性”的问题，如此才能更好地促使学生掌握更多的数学知识，不断深入研究相关数学知识，由此达到提升核心素养的根本目的[3]。教师可以在上述问题的基础上，提出一个难度更高的问题，如下所示。

在△ABC中，已知∠B=60°，最大边与最小边的比为，则三角形的最大角是多少度。

这道题是对正弦定理和余弦定理的综合应用。学生不妨设a为最大边，则由题意可知，，

即 = ， = ，

（3 -）sinA = （3 +）cosA，tanA = 2 +，所以A = 75°。

这样的教学过程由教师通过问题的有效设置，引导学生不断进行深入分析和研究，从而促使学生更好地通过现象看本质。

（四）设计“探究性”问题，增强学生的数学推理能力

数学知识的学习离不开探究，学生只有自主参与探究，才能更好地学习相关数学知识。学生在进行自主探究的过程中，能培养自身的数学思维，逐渐具备自主学习和思考的能力。

例如，甲、乙两人同时从寝室出发到教室，甲一半路程步行，一半路程跑步，乙一半时间步行，一半时间跑步。如果两人步行速度、跑步速度均相同，那么谁先到教室？

学生经过自主探究，利用“不等关系与不等式”的相关知识，将步行速度与跑步速度分别设为V1，V2，而显然V1 < V2，总路程是2s，则甲的时间为，乙用的

时间为，而- = =

> 0，故 > ，所以，乙先到

教室。

通过这样的教学过程，学生能有效理解不等式的基本性质，并为之后的解不等式奠定基础，实现推理能力的持续提高[4]。

（五）设计“开放性”问题，增强学生的思维创新能力

已知3个不等式：①ab > 0;②;③bc > ad，

以其中两个做条件，余下的一个作结论，则能组成多少个正确命题？

此题为开放题，数学教师需要充分认识设问的必要性，在设计问题时，除了要设计“探究性”及“启发性”问题，还要注意问题的“开放性”，由此拓展学生的思维，增强学生的数学推理能力。

首先，学生先对不等式②作等价变形，即> 0。

（1）由ab > 0，bc > ad> 0，即①③②;

（2）由ab > 0，> 0bc - ad >0bc > ad，即①②③;

（3）由bc - ad > 0，> 0ab > 0，即②③①。

所以一共可以组成3个正确命题。这样的教学过程能有效培养学生严谨、规范的学习能力，使其以开放和辩证的眼光看问题，真正达到学以致用的目的[5]。

二、在高中数学解题教学中运用设问渗透数学学科核心素养的策略

（一）教师要加强对学生的科学引导

教师需要在问题设置方面投入更多的精力，并以此为关键，加强对学生核心素养的有效培养。教师需要重点关注问题设置，并且始终以学生为中心，保证问题设置的科学性和合理性。

（二）学生要提高自主学习的积极性

素质教育要求学生能够学会自主学习。教师需要以培養学生的自主学习能力为重要目标，促使学生能够在数学世界中自由地进行探索，从而发现更多的数学乐趣，实现创造能力的提升。

（三）加强师生之间的互动交流

师生在课堂教学中同时扮演着信息生成者、传递者及接受者的角色，这样多个角色之间的互动能够为数学课堂增添更多的生机和活力，活跃课堂气氛，同时，师生也会在互动教学模式的作用下，提高思维的活跃性。同时，教师可以对实际的教学内容进行分析和研究，并提出互动问题，采取更多的互动方式，引导学生积极学习数学知识，进而获得良好的学习效果。

（四）积极创建良好的设问环境

教师虽然需要根据学生的实际情况进行教学引导，但是一味地引导势必会影响学生的自主学习能力，导致学生只是单纯听教师讲课，没有自主思考的过程和机会。因此，教师需要以设问为重点，并积极创设设问环境，从而更好地引导学生进行思考和分析，实现自主学习的价值。

结  语

总而言之，数学解题教学因设问而具有活力，而教师应用各类问题引导学生解题，能帮助学生更好地学习数学知识，实现思维的有效拓展。同时，教师设计启发性、质疑性、提升性、探究性、开放性的问题，能够深化解题教学，提高学生的思维能力。基于设问，学生能够有更加明确的学习方向，进而实现自主学习的价值，增强数学学习体验，实现全方位发展。

[参考文献]

王战雄.“设问式”课堂教学方式的探究：以解三角形的教学片段为例[J].高中数理化，2020（14）：21.

崔成凤.谈“范例”教学设计：以高中数学“算法案例”为例[J].数学大世界，2019（12）：23，22.

范心玮.学生“说”题：高中数学“直线方程”课堂教学探析[J].数学大世界，2020（05）：54-55.

张威.互联网+环境中高中数学课堂教学设计：以“函数图象变换”教学为例[J].高中数学教与学，2019（20）：35-37.

陈仁华.“问”出高效数学课堂：高中数学教学中有效设问的策略探究[J].理科爱好者（教育教学），2021（02）：146-147.

作者简介：刘惠玲（1974.5-），女，福建福清人，

任教于福建省福清融城中学，中学一级教师。