《数学通报》2508号问题的加细与另证

黄传军

(江西赣州师范高等专科学校数学系 341000)

《数学通报》2019年第10期数学问题2508是：

在锐角△ABC中，有

此问题黄兆麟老师把它转化为两个相关不等式，利用三角函数关系和熟知的三角恒等式以及均值不等式和切比雪夫不等式巧妙地给出了证明.因为三角形不等式中一个常见的思路是边角的相互转化，本文就用这一思路把本题角的关系转化为边线关系，并对这一问题进行加细研究，得到了下面的结论：

在锐角△ABC中，有

为了证明结论，先给出Bottema基本不等式以及几个需要用到的三角恒等式.我们知道在△ABC中，若用p,R,r分别表示三角形半周长，外接圆半径，内切圆半径，则有Bottema基本不等式：

以及熟知的恒等式：

下面证明结论中的第一个不等式，

利用三角恒等式我们有

因为△ABC是锐角三角形，

故p2>(2R+r)2，上式去分母得

⟺rRp2+(r2-4R2)rR≥(4R2-rR-2r2)p2-(2R+r)2(4R2-rR-2r2)

⟺(4R2-2rR-2r2)p2≤(r2-4R2)rR+(2R+r)2(4R2-rR-2r2)

⟺(R-r)p2≤4R3-2r2R-r3，

又由Bottema基本不等式右端：

知上式成立只需要证

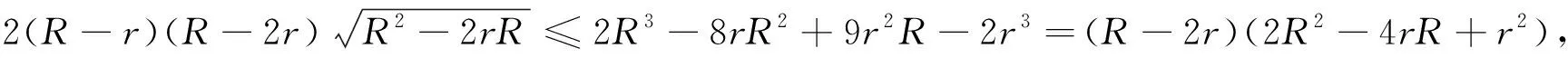
显然R=2r即△ABC是正三角形时，等号成立.否则，上式等价于

⟺(4R2-8rR+4r2)(R2-2rR)≤4R4-16rR3+20r2R2-8r3R+r4

⟺0≤r4，

这显然成立.

再证第二个不等式，

下面证第三个不等式，利用给出的三角恒等式易知：

⟺p2≤12R2-12rR+3r2，

同样由Bottema基本不等式右端：

知上式成立只需要证：

≤12R2-12rR+3r2

=(R-2r)(5R+r)，

显然R=2r即△ABC是正三角形时，等号成立.

再证第四个不等式，同样由三角恒等式知

⟺p2≥12rR+3r2，

这由Bottema基本不等式左端：

知上式成立只需要证：

≥12rR+3r2

显然R=2r即△ABC是正三角形时，等号成立.