关于Milosevic不等式的再研究

李建潮

(浙江省湖州市南浔高级中学 313009)

1 引言

本文约定：a，b，c，R，r，s分别为△ABC的三边长，外接圆半径，内切圆半径，半周长；∑表示循环求和，∏表示循环求积.

文[1]介绍了由D.M.Milosevic提出的如下不等式:

在△ABC中，有

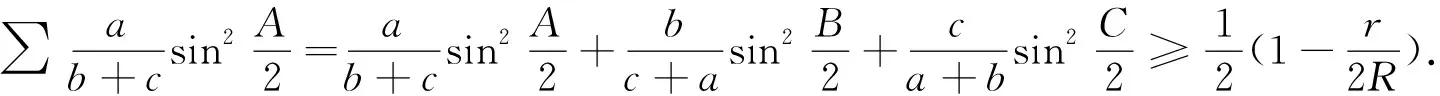
(1)

文[2]给出了不等式⑴的如下加强：

在△ABC中，有

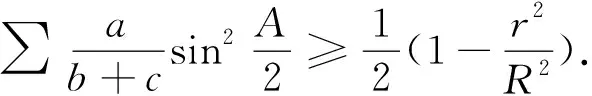
(2)

文[3]介绍了不等式(1)的一个逆向不等式(以下(3)式)及不等式(2)的一个加强(以下(4)式)：在△ABC中，有

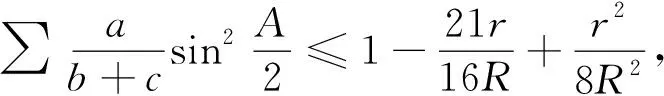
(3)

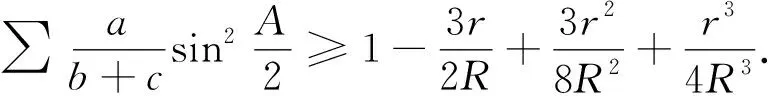
(4)

本文拟对(1)式(的和式)施行三角形恒等变换并通过Gerrestsen不等式16Rr-5r2≤s2≤4R2+4Rr+3r2(见文[4])有机应用于文[3]三角形恒等式：

(5)

建立起不等式(4)与(3)的加强，即

定理1在△ABC中，有

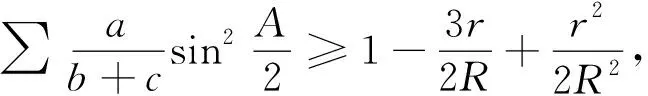
(6)

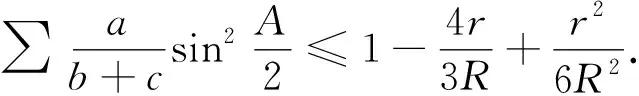
(7)

文末，通过类比获得关于 Milosevic不等式的和谐正切型恒等式及其不等式.

2 关于Milosevic不等式的一个相关三角形恒等式

研究发现关于Milosevic不等式含有以下相关恒等式.

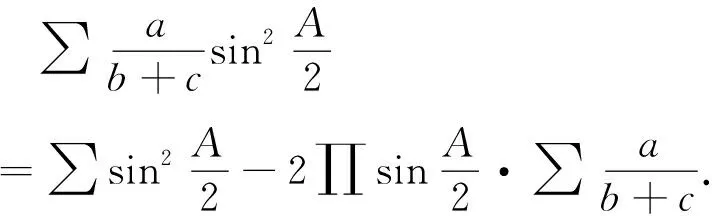
(8)

证明由正弦定理及三角形恒等式

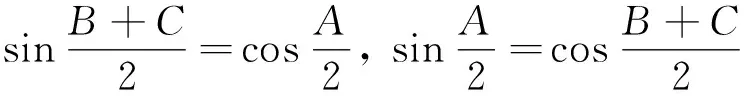
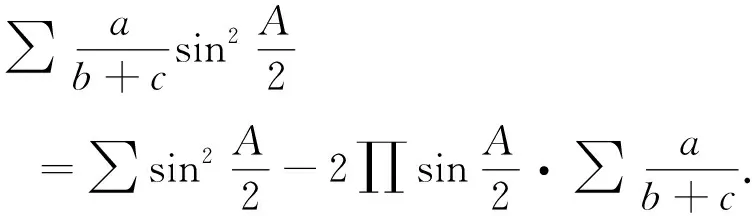
(8)

将三角形恒等式

与(5)式的变式

(9)

一并代入引理1，则引理1成为：

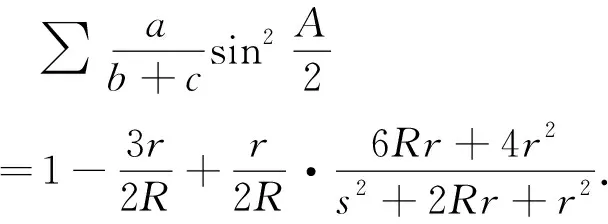
(10)

3 定理1的证明

应用Gerrestsen不等式s2≤4R2+4Rr+3r2,有

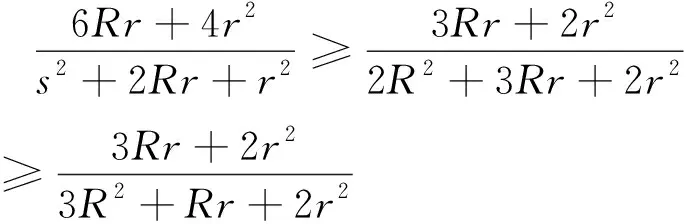
(11)

(11)式代入(10)式，立得式(6).

类似地，应用Gerrestsen不等式s2≥16Rr-5r2,

有

(12)

(11)式代入(10)式，可得式(7)；

至此，定理1得证.

顺便指出，由定理1的证明不难看出，由(11)式与(12)式分别代入(9)式，我们实质上已经得到：

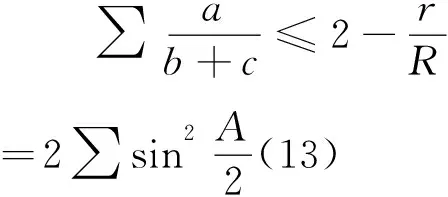
(14)

4 关于Milosevic不等式的正切型恒等式及不等式

通过类比进一步研究发现，还有与引理1极其相似的一个正切型恒等式.

引理3在△ABC中，有

(15)

证明类似于引理1证明的处理方法，有

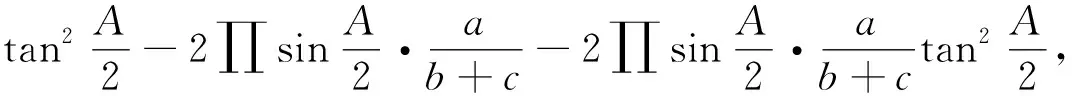
所以

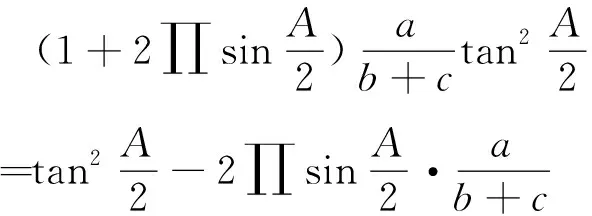
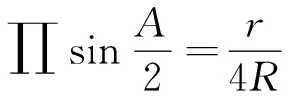
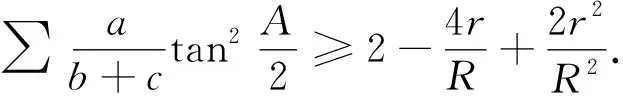
因此，有以下Milosevic不等式的正切型形式：

定理2在△ABC中，有