面向多视图聚类的低秩张量表示学习

余 瑶，杜世强，宋金梅

1.西北民族大学 数学与计算机科学学院，兰州 730030

2.西北民族大学 中国民族信息技术研究院，兰州 730030

聚类是计算机视觉、机器学习和数据挖掘领域中最基本的任务之一，旨在没有先验信息，不需要训练的情况下，将无标签数据根据样本相似性合理的划分为不同的子集，每个子集可称为一个簇。由于大数据背景下，获取有标签数据是一个耗时耗力成本高昂的工作，所以聚类作为一种重要的无监督学习方法变得非常重要。在过去的几十年里，各种各样的聚类方法相继被提出，K-means[1]是最常用的聚类方法，目的是学到一个聚类中心，使得簇内的数据距中心较近；标准谱聚类（SPC）[2]首先根据样本之间的相似度构造一个相似矩阵，然后建立一个无向加权图，最后利用图拉普拉斯算子的性质学习相似矩阵。现有的大多数聚类算法来源于SPC，其中最重要的一步是构造数据点间的相似度矩阵，根据构造方式的不同，基于SPC 的聚类方法主要分为两类，包括基于自表示的子空间聚类方法[3-4]和基于图的聚类方法。

基于自表示的方法是将样本点表示为同一子空间内其他点的线性组合，然后通过系数矩阵构造相似度矩阵。文献[5]提出低秩子空间聚类（LRR），在自表示矩阵上施加低秩约束来捕获全局结构，但聚类的精度需要在子空间独立并且数据充足的情况下才能保证，这种假设条件对于现实数据集来说过于严苛。文献[6]等放宽约束条件，引入稀疏性准则提出了稀疏子空间聚类（SSC）算法，将每个数据点表示为其他数据点的稀疏线性组合来捕获数据的局部结构。文献[7]利用低秩和稀疏约束的互补度量子空间聚类里的自表示系数，用得到的系数矩阵来计算相似度矩阵进而执行谱聚类得到最终结果。基于图的聚类方法重点是如何学习到一个高质量的图，然后在该图上使用谱聚类算法来获得最终结果。文献[8]提出一种鲁棒图学习（RGC）算法，自适应的去除原始数据中的噪声，从真实数据中学习精确的图。

另外，现实世界中充满着各种复杂多样的数据，获取数据的来源也各不相同。例如，一个客观对象可以由文字、图像、音频或视频来描述。多视图信息的充分利用更能够提升聚类性能，因此许多多视图聚类方法从这些流行的单视图方法中衍生出来。多视图子空间学习方法主要基于自表示来探索样本之间的关系，文献[9]提出了多视图子空间聚类（MVSC）方法，对每个视图的系数矩阵进行谱聚类以获得不同视图间共同的聚类结构。文献[10]利用系数矩阵的稀疏性和不同视图间的互补信息提出了排他性一致性多视图子空间聚类。文献[11]将低秩稀疏子空间聚类（LRSSC）[4]算法拓展到多视图领域提出了多视图低秩稀疏子空间聚类算法（MLRSSC），不仅能从多个视图中学习到更精确的图，还能捕获数据的全局和局部结构。但有些多视图聚类方法仅探索视图间的一致性而忽视了每个视图的局部结构，文献[12]提出为不同的特征分配权重并在各个视图特定的自表示空间中获取局部信息进而提高聚类性能。基于图学习的多视图聚类方法中，文献[13]提出以欧式距离为度量标准，自适应的构造一个关系矩阵，称为自适应近邻学习（ANGL）。通过ANGL 融合多个视图的原始矩阵，得到一个共识关系图，从而提出自适应近邻多视图学习（MLAN）[14]算法。由于大多算法假设不同特征重要性相同，而在现实中这一假设并不完全适用，文献[15]提出了自适应近邻加权聚类算法（SWCAN），为不同特征分配权重，在学习相似图的同时将样本划分为多个簇。现实数据中，有些图掺杂了较大的噪声，这会降低聚类性能，所以文献[16]提出一种基于低秩和稀疏分解的马尔可夫链方法用于鲁棒多视图谱聚类（RMSC）来克服这一缺陷。RMSC 先在每个单视图上构造转移概率矩阵，然后用从这些矩阵中恢复出的低秩转移概率矩阵作为标准马尔可夫链聚类方法的输入。

上述多视图聚类方法已经取得了良好的效果，但还是没有有效地利用多视图数据间的互补信息，忽视了多视图数据的高阶相关性。针对这一问题，文献[17]提出了基于Tucker 分解的低秩张量约束多视图子空间聚类（LTMSC），但Tucker分解并不是秩函数的凸松弛，所以文献[18]进一步提出了基于张量奇异值分解的多视图子空间聚类，通过基于t-SVD的核范数对张量施加一种新型的低秩约束，确保了多个视图之间的一致性。但大多基于张量核范数最小化的聚类方法同等的对待每一个奇异值，限制了处理问题的灵活性，所以文献[19]充分利用奇异值的先验信息，提出了基于张量加权核范数的多视图聚类方法。文献[20]提出了本质张量学习的多视图谱聚类（ETLMSC），主要学习一个具有低秩约束的本质张量，然后将其作为基于马尔科夫链的谱聚类的输入。文献[21]进一步提出了基于截断核范数的低秩张量分解的多视图谱聚类算法。

基于上述研究发现多视图聚类算法中相似矩阵和图的质量至关重要，但部分算法构造的图由于受噪声和异常值的影响而不具有鲁棒性且无法充分利用多视图的互补信息，而基于张量的算法又通常使用原始数据构造张量且计算复杂度高。针对以上问题，本文提出一种面向多视图聚类的低秩张量表示学习（LRTRL-MVC）算法，主要贡献为：

（1）将鲁棒图学习扩展到多视图数据，在去除噪声和异常值影响的同时进一步利用多视图的互补信息，获得更加精确揭示样本之间关系的亲和图，提升聚类性能。

（2）利用各视图数据获得的鲁棒图构造3 阶张量，挖掘多视图数据间的高阶相关性。

（3）选用基于张量奇异值分解（t-SVD）的核范数来保持本质张量的低秩性质，以便更好地捕获多视图共用的类别信息。

（4）提出了一种基于交替方向乘子法（ADMM）的优化算法来求解目标函数。与其他相关的最好多视图聚类算法相比，提出的方法在4个不同的数据集上取得了最好的聚类效果。

1 相关符号和定义

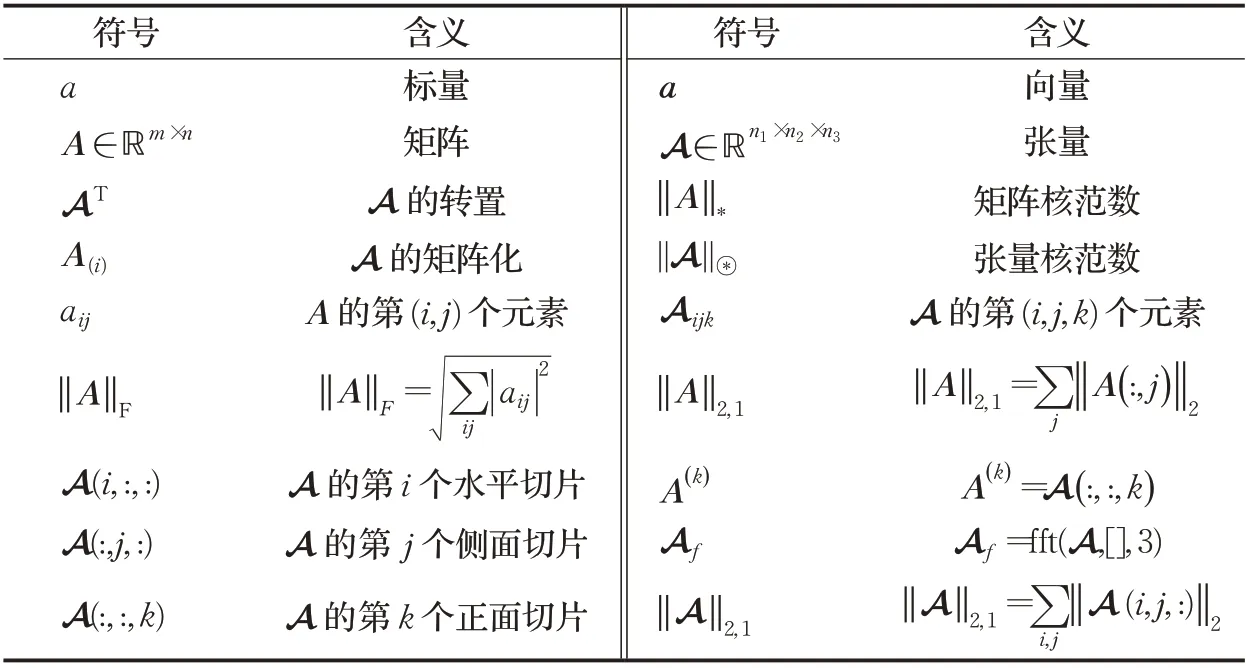
表1 相关符号Table 1 Summary of notations

定义1（f-对角张量[21]）对于一个3 阶张量，若其所有正面切片都是对角矩阵，则称为f-对角张量。

定义2（单位张量[21]）对于张量I∈ℝn×n×n3，第一个正面切片是大小为n×n的单位矩阵，其他所有正面切片均为0矩阵。

定义3（张量积t-product[22]）假设张量A∈ℝn1×m×n3，B∈ℝm×n2×n3，则张量积A∗B 是一个大小为n1×n2×n3的张量，且：

2 面向多视图聚类的低秩张量表示学习

本文提出的算法由两部分组成，第一部分将鲁棒图学习扩展到多视图中，利用鲁棒主成分分析[23]（RPCA）的思想，将多视图数据的每个视图矩阵分解成低秩矩阵和稀疏矩阵，并在干净的低秩矩阵上利用自适应近邻法构造鲁棒图。第二部分用第一部分得到的图作为输入，计算出相应的转移概率矩阵，再堆叠构建一个3阶张量并将张量沿第三维旋转，然后对张量进行t-SVD 分解，得到一个低秩张量和一个噪声张量，最后在低秩张量上执行马尔可夫谱聚类得到最终的聚类结果，本文算法框架如图1所示。

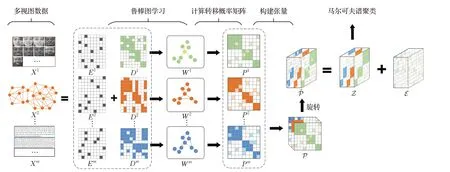
图1 LRTRL-MVC算法框架Fig.1 Framewok of LRTRL-MVC algorithm

2.1 多视图鲁棒图学习

2.1.1 目标函数

2.1.2 目标函数求解

2.2 基于马尔可夫链的谱聚类

2.3 低秩张量学习

2.3.1 目标函数

根据算法2，在基于马尔可夫链的谱聚类方法[28]中，转移概率矩阵直接影响着聚类性能。同样对于面向多视图聚类的马尔可夫链谱聚类方法[16，19，29]，转移概率矩阵对聚类结果也具有重要的影响，因此如何基于多视图来学习谱聚类的转移概率矩阵是要解决的主要问题。其中一个代表性方法RMSC[16]将每个视图下的转移概率矩阵Pi分解为共享概率矩阵Z和视图特定的噪声矩阵Ei，以此来获取共享信息。但是该方式忽略了每个视图中包含的对聚类有用的特殊信息，所以，将每个Pi分成两部分，即Pi=Zi+Ei，然后分别收集堆叠所有的Zi和Ei来构造3阶张量Z 和E，进而在张量形式下揭示不同视图之间的高阶相关性。由于不同视图是同一对象的不同表示形式，因此，不同视图下的低秩部分Zi通常具有相同的类别属性。另外，样本类别数目通常比样本数目少的多，所以，由不同视图下的低秩部分Zi构成的张量Z 具有低秩结构，使用基于t-SVD 的张量核范数|| ||⊛来度量。此外对于噪声项，由于噪声样本一般是稀疏的，所以用对异常值和噪声具有较强鲁棒性的ℓ2,1范数来度量。不直接使用转移概率张量P∈ℝn×n×m，而是将其沿第三维即特征维旋转，这种旋转操作在Mtalab 中可以通过fft 功能轻松实现，且沿特征维的快速傅里叶变换不仅保持了视图之间的关系，还大大降低了优化求解中的计算复杂度。得到张量形式的目标函数为：

3 实验结果与分析

3.1 实验设置

3.1.1 数据集

为验证算法的有效性，在4 个数据集上进行实验，分别是BBCSport、Newsgroups data set（NGs）、Yale 和MSRCv1。

BBCSport[20]（http：//mlg.ucd.ie/datasets/bbc.html）数据集总共有2种不同的视图，包含来自英国广播公司体育网站的737 份文件，对应于田径、板球、足球、橄榄球和网球5个热门领域的体育新闻。

NGs（http：//qwone.com/～jason/20Newsgroups）是20个新闻组数据集的子集，共有3 个视图。由500 个新闻组文档组成。每个原始文档都用3 种不同的特征提取方法进行预处理。

Yale（http：//vision.ucsd.edu/datasets/yale_face_dataset_original）人脸数据库包含3 个视图，有15 个人的165 张灰度图像。每个主题包括11个不同的表达和配置的图像。本文提取了3种类型的特征。

MSRCv1[10]数据集有5 个视图，包含由7 个类别组成的210 幅图像，并且本文对于每幅图像选择5 个特征向量。

3.1.2 评价指标

为了综合评估聚类的性能，本文采用3个常用的评价指标对结果进行度量，分别是精确度[18]（ACC）、纯度[18]（Purity）和归一化互信息[18]（NMI）。对于所有指标，值越高表示性能越好。

3.1.3 对比算法

为了说明提出算法的有效性，我们将在实验数据集上与下列5个相关算法进行对比：

（1）低秩表示（LRRbest）[5]，对每个视图采用低秩表示算法，选择最优结果。

（2）鲁棒图学习（RGCbest）[8]，自适应的去除原始数据中的噪声和异常值，从每个视图中学习到最可靠的图进行聚类，选择最优结果。

（3）基于自适应近邻的多视图学习（MLAN）[14]，同时进行多视图聚类、半监督分类和局部流形结构学习，得到最优图直接划分聚类。

（4）同时学习特征权重和局部结构的多视图子空间聚类（JFLMSC）[12]，将特征的自适应局部学习、自表示学习和权重学习结合到一个框架中，利用每个视图的全局和局部结构进行多视图子空间聚类。

（5）本质张量学习用于多视图谱聚类（ETLMSC）[20]，学习一个本质张量用于基于马尔可夫链的谱聚类，揭示多视图表示的高阶相关性。

3.2 实验结果与分析

3.2.1 实验结果

分别在4个数据集上对5个算法和本文提出的算法进行实验，为减小实验的误差，对不同的算法单独调整参数直至最优，不同数据集上的实验结果分别如表2～5所示，最优结果加粗表示。

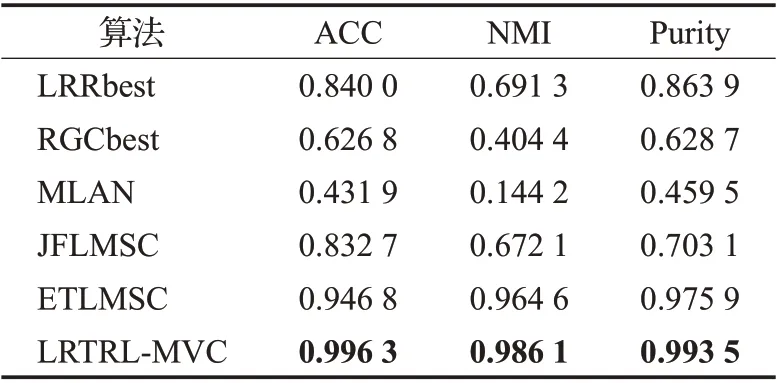
表2 数据集BBCSport上的实验结果Table 2 Experimental results on BBCSport

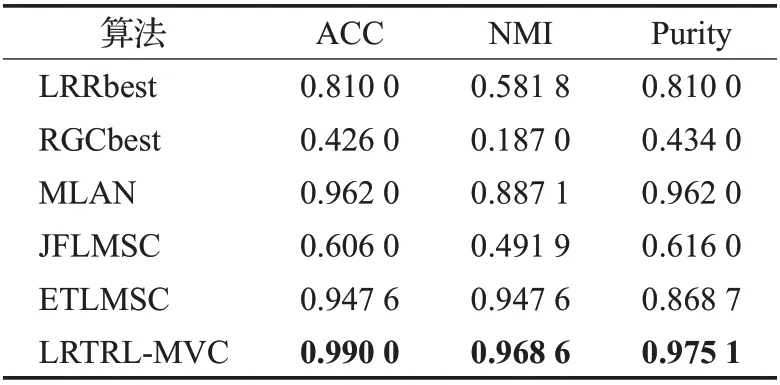
表3 数据集NGs上的实验结果Table 3 Experimental results on NGs

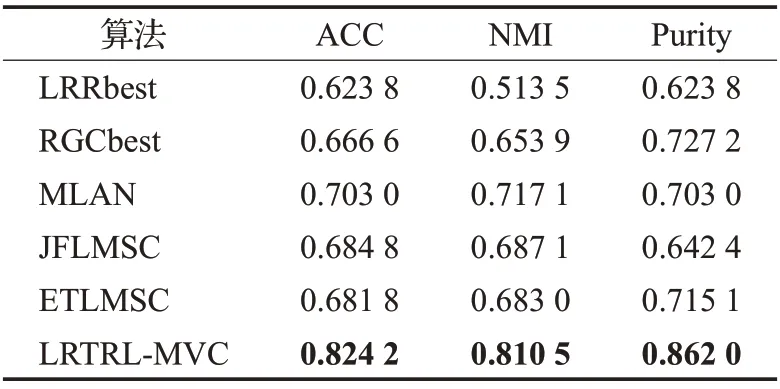
表4 数据集Yale上的实验结果Table 4 Experimental results on Yale

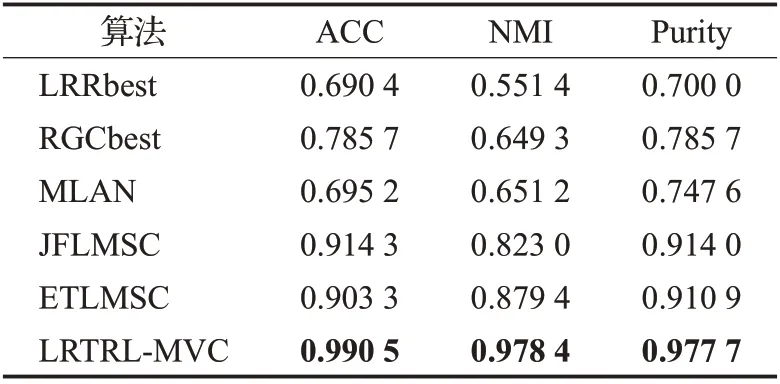
表5 数据集MSRCv1上的实验结果Table 5 Experimental results on MSRCv1

从表2～5中可以看出，4个数据集中，本文提出的算法都取得了最佳聚类性能。例如在Yale人脸数据集上，与相应的次优算法MLAN相比，本文提出的方法在3个评价指标ACC、NMI和Purity上分别提升了17、13和22个百分点。所提算法的纯度在4 个数据集上相比于ETLMSC 方法，分别提高了1、12、20 和7 个百分点。提出的算法与单视图的LRR、RGC算法相比，在性能上均取得了较大的提升，主要是由于单视图聚类算法仅仅利用了单个视图的信息，即使选择最优的视图进行聚类，在性能上也无法取得更好的结果。与在原始数据上直接学习图的多视图聚类算法MLAN 相比，本文算法是在干净的低秩数据上学习图，使得聚类效果有了进一步的提升。与JFLMSC算法相比，通过构造张量进一步探索到多视图数据的高阶相关性，使得聚类准确性更高。与基于张量的方法ETLMSC 相比，本文方法仍体现出优越性，主要归功于转移概率矩阵构造的可靠性以及高阶相关性的有效探索。由上述实验可以发现，与其他传统算法相比，本文算法在不同类型数据集和不同评价指标上都有更优异的表现。

3.2.2 参数分析

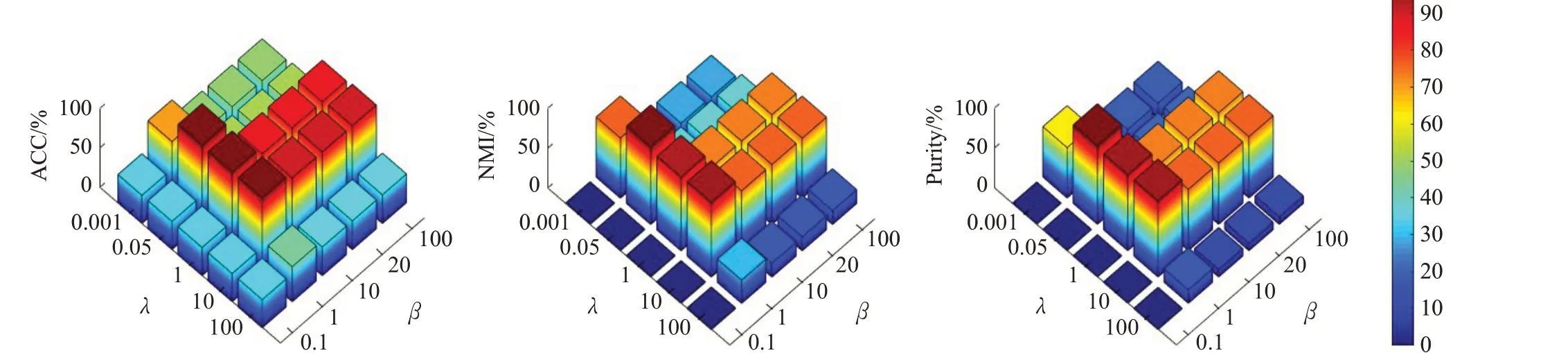
图2 参数β 和λ 对BBCSport数据集的影响Fig.2 Influence of β and λ values on BBCSport dataset

3.2.3 复杂度分析

本文提出的算法的主要计算量来自低秩张量学习每次迭代过程中Z和E 的求解，优化求解张量E 的时间复杂度为O(mn2)。而对于张量Z，一方面，沿第3维的傅里叶变换和逆傅里叶变换时间复杂度为O(mn2lbn)，另一方面，在傅里叶域计算每个正面切片奇异值分解的时间复杂度为O(mn2)，所以求解计算Z的总时间复杂度为O(mn2+mn2lbn) 。通常视图数m远远小于样本n，那么m≤lbn，所以相较于不进行张量旋转所需要的计算复杂度O(m2n2lbn)，张量旋转操作降低了计算复杂度。其次算法复杂度还涉及到多视图鲁棒图学习和基于马尔可夫谱聚类中的奇异值分解和矩阵求逆的操作，一般他们的计算复杂度为O(n3)。记迭代次数为t，提出的算法总的计算复杂度为O(n3+tmn2(m+lb(n)))。

表6显示了提出的算法和5种对比算法的时间复杂度以及在4 个数据集上运行10 次的平均时间，其中dv表示第v个视图特征向量的维数，m和n分别为视图数和样本数，r是样本数据矩阵的秩，平均运行时间以s 为计量单位。虽然MLAN 和ETLMSC 算法所需运行时间较短，但其聚类性能不如本文提出的算法。与比较算法中运行时间较长的两个算法RGC 和JFLMSC 相比，提出算法的运行时间在BBCSport 和MSRCv1 数据集上多于RGC 和JFLMSC，但是在NGs 和Yale 数据集上显著少于RGC 和JFLMSC。在实际应用中，提出的LRTRL-MVC 能够在可接受的时间范围内达到更好聚类效果。

3.3 可视化结果

为了更直观地看到聚类结果，将面向多视图聚类的低秩张量表示学习算法与其他对比算法在MSRCv1 数据集上的聚类结果进行可视化。先通过tSNE方法将高维特征映射到二维子空间，再利用算法得到的聚类结果对映射后的二维数据进行着色，由此直观地显示出算法的聚类性能。从图3中可以观察到，本文提出的算法能有效地将相似样本聚集到一个簇中，体现出优越的聚类性能。

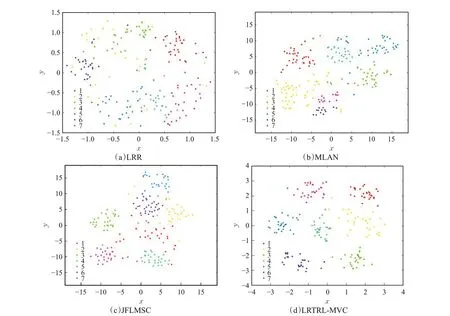
图3 MSRCv1数据集上算法可视化结果Fig.3 Visualization results of algorithm on MSRCv1 dataset

4 结论

本文提出了一种面向多视图聚类的低秩张量表示学习算法，通过把鲁棒主成分分析和自适应近邻学习融合到一个框架将鲁棒图学习扩展到多视图，充分利用了多视图数据的互补信息。然后利用精确的鲁棒图计算转移概率矩阵进而构造3 阶张量。通过基于张量奇异值分解的核范数约束低秩张量来揭示多视图间的高阶相关性，最后利用马尔可夫谱聚类获得最终的聚类结果。在BBCSport、NGs、Yale 和MSRCv1 数据集的聚类实验中，与算法LRR、SPC、MLAN、JFLMSC和ETLMSC相比，不论是数值指标还是可视化结果，本文提出的算法都获得了更好的聚类结果。