脑电信号多维特征融合与分类算法研究

朱永清，王文格

湖南大学 机械与运载工程学院，长沙 410006

脑机接口（brain-computer interface，BCI）是直接通过人类大脑信号确定其意图，实现人脑与外部设备的通信和控制[1]。BCI 在脑控轮椅[2]、疾病康复[3]、神经假肢[4]等领域具有广泛地应用前景，为残障人群提供有效生活保障。目前，BCI技术最大难点在于如何提高脑电信号识别准确率，因此脑电信号（electroencephalogram，EEG）的特征提取算法优化以及分类器改进是目前BCI 研究的重点，特别是在运动想象脑电信号领域。

近年来，由于单一特征只能表征特定的脑电信息，而多特征融合因能包含不同维度的有效脑电信息，成为运动想象多分类特征提取的研究热点之一。其中具有代表性的有：李明爱等[5]提出一种基于希尔伯特-黄变换（Hilbert-Huang transform，HHT）与共空域子空间分解算法（CSSD）的特征提取算法，提取希尔伯特瞬时能量谱和边际能量谱作为时频特征，并提取空域特征，将融合特征使用矢量化神经网络分类器进行分类。Chen等[6]提出融合香农熵、小波熵和样本熵作为运动想象脑电特征。杨默涵等[7]提出EEMD 与近似熵相结合的多特征提取方法。

在运动想象分类识别中，常用的分类器有支持向量机（support vector machines，SVM）[8]和线性判别分析（linear discriminant analysis，LDA），然而在多任务分类情况下，两者容易出现无法分类现象，而且随着类别的增多，准确率随之下降，而深度学习因具有分类精度高且能够自动提取最优化特征和解码等优势，逐渐被应用于运动想象分类识别。文献[9]提出具有滑动裁剪策略的深度递归神经网络（recurrent neural network，RNN）应用于脑电分类，并将能控循环单元和长短期记忆单元应用于RNN 架构。文献[10]提出了使用连续小波变换提取脑电信号作为卷积神经网络（convolutional neural network，CNN）的输入特征进行分类。文献[11]使用多层半监督极限学习机（hierarchical semi-supervised extreme learning machine，HSS-ELM）作为分类器，但识别准确率提升并不明显。

为了改善运动想象分类准确率，本文提出利用脑电信号的时-频-空以及非线性动力学4个维度的特征进行加权融合，提取的特征分别为共空间特征，能量特征，边际谱熵特征和非线性动力学特征；构造CNN分类器，将融合特征作为CNN 分类器的输入特征，在运动想象多任务识别中取得了较好的效果。

1 相关理论

1.1 OVO-CSP

“一对一”共空间模式（one versus one-common spatial pattern，OVO-CSP）[12]是一种多任务运动想象脑电信号特征提取算法，在多任务分类中取得了良好的效果，该算法思想是将多分类问题转化成若干个二分类问题。

这里使用传统二分类CSP 算法进行说明，假设X1,X2∈RN×T是两分类运动想象的多通道诱发响应时空信号矩阵，其中N为电极通道数，T为采样长度。则协方差矩阵如下：

1.2 希尔伯特-黄变换

1.3 小波包变换

小波包变换（wavelet packet transform，WPT）具有无冗余、无疏漏优势，可以对脑电信号局部时频分析。利用小波包变换可以对运动想象EEG信号进行细致有效的分解，能够显著提升运动想象脑电特征分类的准确率。函数的表达式如下[15]：

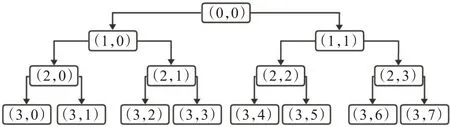
图1 小波树分解图Fig.1 Diagram of wavelet tree decomposition

1.4 非线性动力学特征

2 特征提取与融合

2.1 数据来源

数据采用2008 年第四届国际BCI 竞赛中，由Graz科技大学提供的脑电数据集（Dataset 2a）[19]，该数据集由9 名受试者提供4 种不同的运动想象任务，包括想象左手、右手、脚和舌头的运动。脑电信号共采集22 个EEG 通道，3 个EOG 通道，每个受试者共拥有训练集和测试集两组数据，每组数据共288 次运动想象，每个运动想象任务随机生成。

实验范式如图2所示，实验开始时（t=0 s），屏幕出现十字交叉并发出运动想象提示音，2 s 后出现一个持续1.25 s的向左、右、上、下的箭头（分别表示左手、右手、舌头、脚）提示受试者开始运动想象，没有提供反馈；受试者需要一直执行运动想象到t=6 s，接着是1.5 s的休息时间，然后不断重复上述过程直至结束。

图2 实验范式时序图Fig.2 Sequence diagram of experimental paradigm

2.2 预处理

在特征提取前，需要对原始脑电数据集进行预处理，才能更有效地提取EEG信号特征。根据图2实验范式可知，有效脑电信号主要集中在运动想象任务开始的3～6 s，因此提取运动想象3～6 s 的采样数据作为分类识别数据，将EEG 信号中含有“NaN”的数据置为0[20]。由于运动想象产生的ERD/ERS主要分布在μ节律（8～13 Hz）和β节律（14～30 Hz）[21]，故对运动想象信号进行8～30 Hz的5阶巴特沃斯带通滤波，可以有效提高EEG信号的信噪比。

2.3 特征提取

数据集的采样频率为250 Hz，故选取dB4小波作为小波包变换的基函数，将预处理后的EEG信号分解为4层小波包，得到16 个频率分量，其中最小分辨率f=7.8 Hz。根据表1 的小波子带频率范围可以得知节点（4，1），（4，2），（4，3）的频带范围为7.8～31.2 Hz，基本涵盖运动想象脑电信号的有效信息，因此选取节点（4，1），（4，2），（4，3）对运动想象脑电信号进行重构。

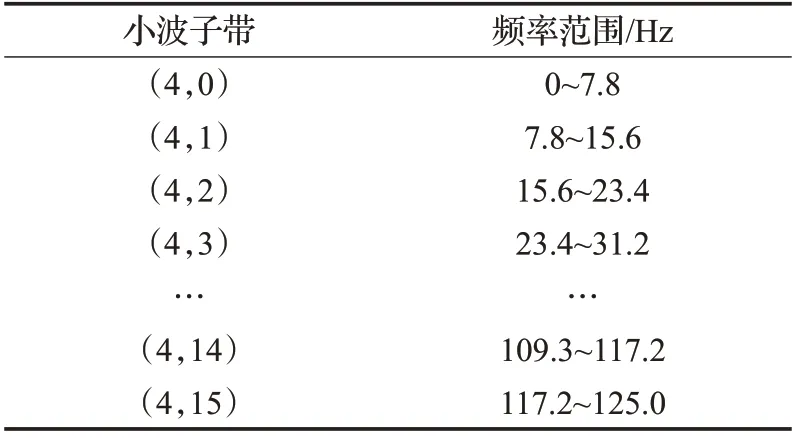
表1 小波子频带频率范围Table 1 Range of wavelet sub-bands frequency

将重构后的EEG 信号分别进行相应的特征提取，得到不同维度的有效脑电特征，具体算法流程如图3所示。

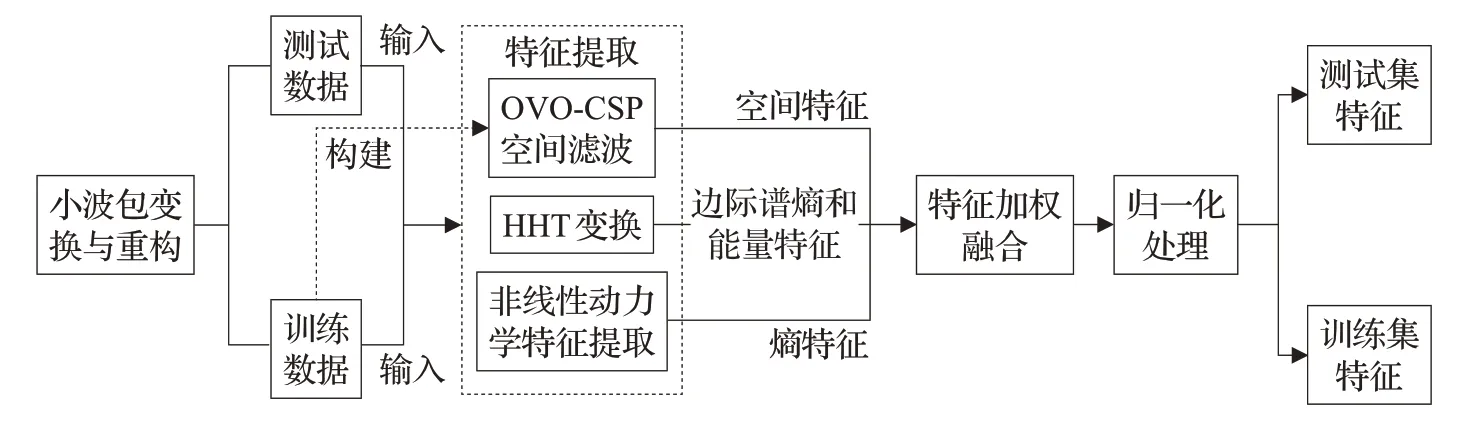
图3 特征提取算法流程Fig.3 Flow of feature extraction algorithm

提取共空间特征时，使用训练数据构建OVO-CSP的空间滤波器，由于数据集为4 分类EEG 信号，需要构建6 个空间滤波器。将EEG 数据分别输入各个空间滤波器，可得共空间特征F1，F1为6×22 的共空间特征矩阵。

提取能量特征前，需要对EEG 信号进行EMD 分解，分解得到的IMF 如图4（a）所示。由图可看出EEG信号的能量主要集中在前3 阶的IMF，因此可以使用IMF1～IMF3 正向重构信号，重构后的信号含有大量有效脑电信号，重构信号如图4（b）所示。对于重构后的信号首先提取其能量特征，其中包含22 个通道的能量特征，将脑电信号的能量特征记为F2；再对重构的信号进行Hilbert 变换，得到时频谱和边际谱，并提取边际谱熵特征，每次样本得到22通道的边际谱熵特征，记为F3，如图5 所示，从边际谱图可以看出，重构信号能量主要集中在0～30 Hz之间，与运动想象脑电信号分布在μ节律和β节律相符。

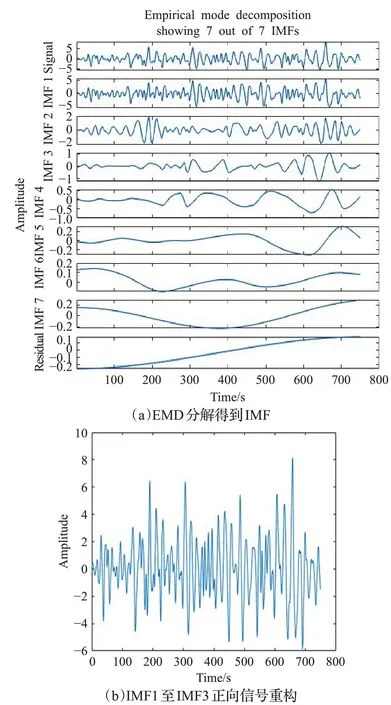
图4 EMD分解和正向重构Fig.4 EMD decomposition and forward reconstruction

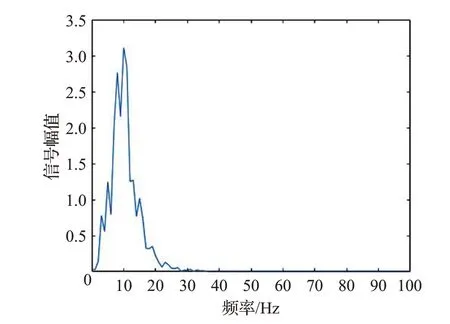
图5 边际谱图Fig.5 Marginal spectrogram

最后，提取小波包重构后脑电信号的非线性动力学特征，包括近似熵特征、模糊熵特征和样本熵特征。3种非线性动力学特征的维数和相似容限值分别取值为m=3，r=0.5，得到的非线性动力学特征记为F4，其为3×22的矩阵。

2.4 特征融合

通过特征提取得到F1、F2、F3、F4这4 种特征，对上述4种特征进行如式（11）的加权融合，最终得到特征融合矩阵F，其中c1、c2、c3和c4为每种特征所赋予的权重值。对F进行归一化处理后，即可输入至卷积神经网络分类器进行分类识别。

3 基于卷积神经网络的EEG信号分类识别

3.1 卷积神经网络结构

本章将构建CNN分类器对四分类运动想象数据集进行分类识别，构建的CNN 模型基于二维特征输入的神经网络，网络模型如图6所示。

图6 CNN网络结构Fig.6 CNN architecture

（1）第一层为输入层，输入特征大小为11×22。

（2）接下来共有3个卷积层，第1个卷积层的卷积核大小为12×12，共有24 个卷积核；第2 个卷积层的卷积核大小为8×8，共有48 个卷积核；第3 个卷积层的卷积核大小为4×4，共有96个卷积核。每个卷积层后都跟着一个归一化层和最大池化层，其中池化核大小为2×2，激活函数使用ReLU函数。

（3）最后是全连接层、激活层和分类层，其中全连接层为3个隐含层，神经元个数分别为192、28和4，通过分类层输出CNN所识别的脑电意图。

3.2 基于融合特征的CNN分类识别

将9个志愿者的数据集以8∶2划分为训练集和测试集，因此每个志愿者共有230个训练样本和58个测试样本。分析融合特征在CNN 分类器的分类效果之前，需要对式（11）的4 个权重参数取值进行分析。对于权重取值，可以运用控制单一变量法，分别对式（11）的4 个权重取值分析。由于不同维度的特征值存在数量级差异，如果差异过大将导致融合特征携带信息丢失，因此依次将其中一个权重设置成以100，101，…，105方式递增，固定其他3个权重，使用相应的融合特征对卷积神经网络完成训练，输入测试集的特征矩阵至CNN分类器，得到结果如图7 所示。最初先固定权重c2=c3=c4=1，由图7（a）可知，c1=104时分类器表现最佳。因此将c1置为104对c2进行分析，由图7（b）得c2=1 时识别准确率最佳。依次类推，分别得到c3=1,c4=104。

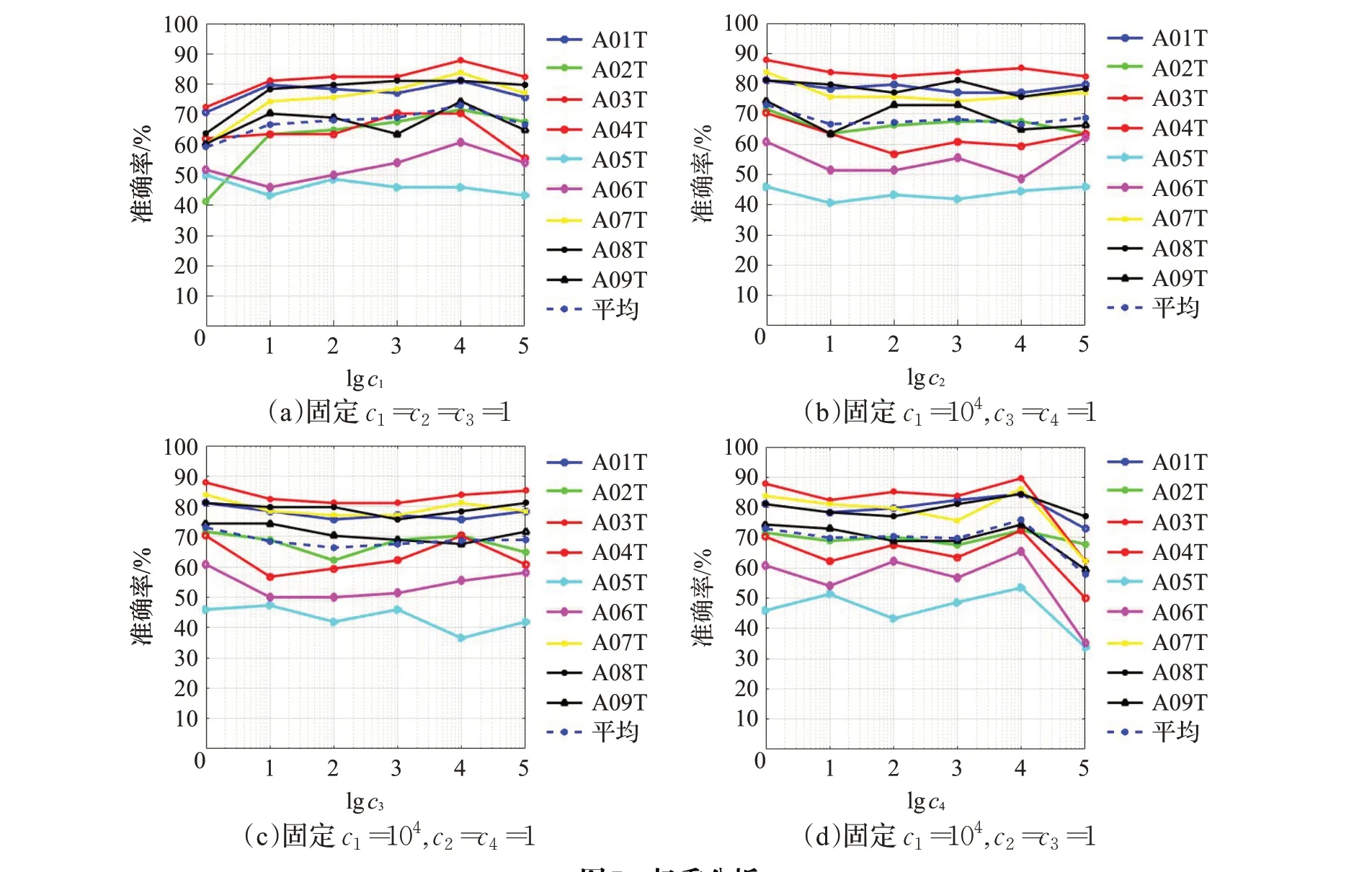
图7 权重分析Fig.7 Weight analysis

通过以上权值分析，发现当权值为c1=104,c2=1,c3=1,c4=104时分类器的识别效果较好。同时，分别使4 个权重中的3 个为1，另一个权重设为自增变量，使用CNN分类器在训练测试比例不变的情况下迭代300次，选取最高识别率，最终得到4 个权重参数的平均曲线图，如图8所示。

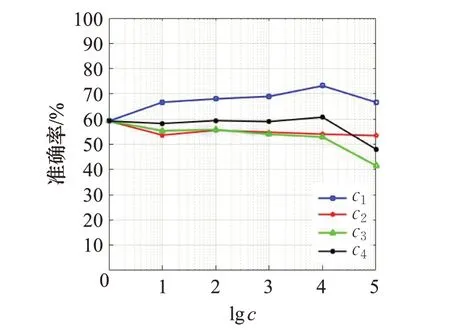
图8 4个权值的平均曲线Fig.8 Average curve of four weights

由图8 可以发现，c2和c3曲线均呈下降趋势，随着c2和c3的增长，CNN 分类器的识别准确率有所下降。而c1和c4均在104时得到较好结果，因此，就整体平均水平而言，融合特征的权值在该取值策略下取值为c1=104,c2=1,c3=1,c4=104时可以得到较好的分类结果。然而由图7可以发现，就个体而言在权重参数取值并不唯一，可以在不同其他取值情况下得到更好或者相同的识别效果，如图7（b）的A06T 曲线和图7（d）的A09T曲线。

最终得到每位志愿者在CNN分类器的识别准确率如表2所示，与此同时得到SVM、BP分类器在该参数条件下也得到较好结果。其中SVM的输入为11×22，输出为识别结果；BP 分类器的输入层、隐藏层、输出层神经元个数分别为242、34、4。以上分类器均是在参数最优情况下获得分类准确率。

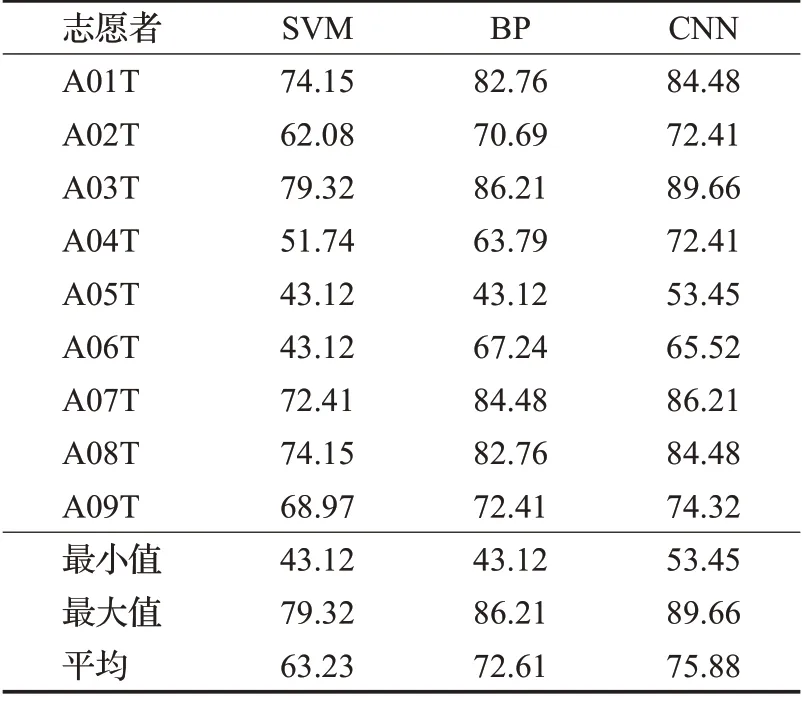
表2 融合特征下不同分类器的对比Table 2 Comparison of different classifiers under fusion features%

由表2 可知，CNN 分类器的平均分类准确率比SVM高12.65个百分点，比BP高3.27个百分点，其最高准确率比BP 高3.45 个百分点，比SVM 高10.34 个百分点，而最低分类准确率要比两者高10.33 个百分点。对比CNN和SVM，9位志愿者的分类精度均高于SVM；再对比CNN 与BP，仅A07T 志愿者高于CNN。可以看出CNN的整体分类性能是要比SVM和BP神经网络优越，是一种分类效果好、准确度高的机器学习算法，而且在独立个体的运动想象脑电信号分类中表象良好。因此，选择CNN分类器作为运动想象多任务识别可以有效提高识别准确率。

3.3 融合特征与单一特征对比

常用的特征提取算法是CSP共空间特征提取，该算法属于单一特征提取算法，为与融合特征对比，同样进行小波包变换，然后提取其共空间特征。提取的共空间特征分别使用SVM、BP和CNN算法来训练分类器并进行测试，此时3 种分类器的输入特征大小为6×22，得到每位志愿者的测试准确率如表3 所示。由表3 可以发现，以单一特征（WPT+CSP 特征提取）作为分类器的特征输入时，仍是CNN分类器平均分类准确率最高，可以说明CNN分类器在不同的特征输入下表现出良好的分类情况。通过对比表2和表3可以发现，虽然SVM分类器在两种特征输入下的平均分类效果并无明显区别，甚至前者略低于后者；但BP和CNN分类器以融合特征作为输入，得到的分类准确率明显要高于WPT+CSP 特征，对CNN 分类器来说，前者得到的平均准确率为75.88%，比后者高6.30 个百分点，说明融合特征能够携带更多的脑电信息，能够更好地提高运动想象脑电识别准确率，且明显优于WPT+CSP特征分类识别。

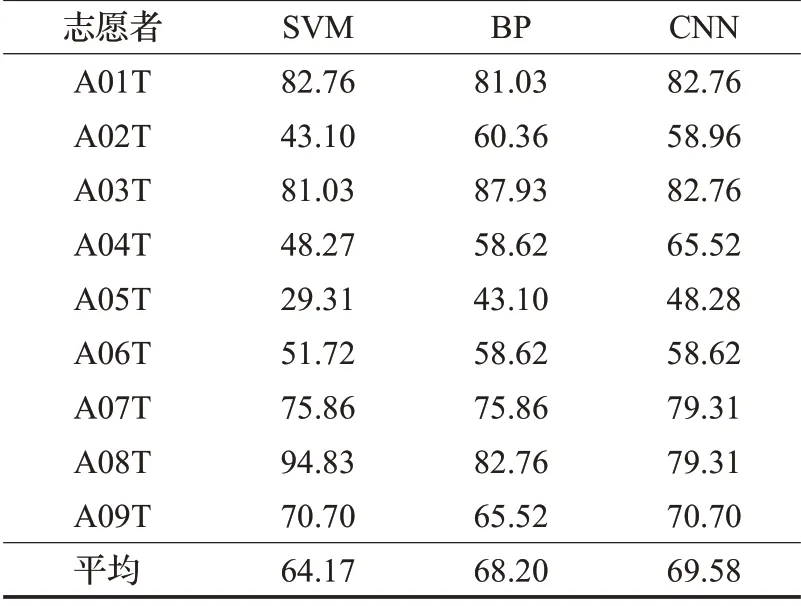
表3 单一特征下3种分类器的分类性能Table 3 Classification performance of three classifiers under single feature%

4 实验结果分析

在融合特征权值的取值分析过程中，得到如表3所示的融合特征在CNN分类器的分类结果。分类结果采用目前通用的Kappa系数进行衡量：

式中，p0为准确率。由式( )12 可知，Kappa 系数越高，代表对应的识别率越高。9位志愿者在特征融合算法下得到的Kappa 系数如表4 所示，其中A03T 最高为0.87，A05T 最低为0.46，得到该算法平均Kappa 系数为0.70，处于分类准确率相对较高的水平。

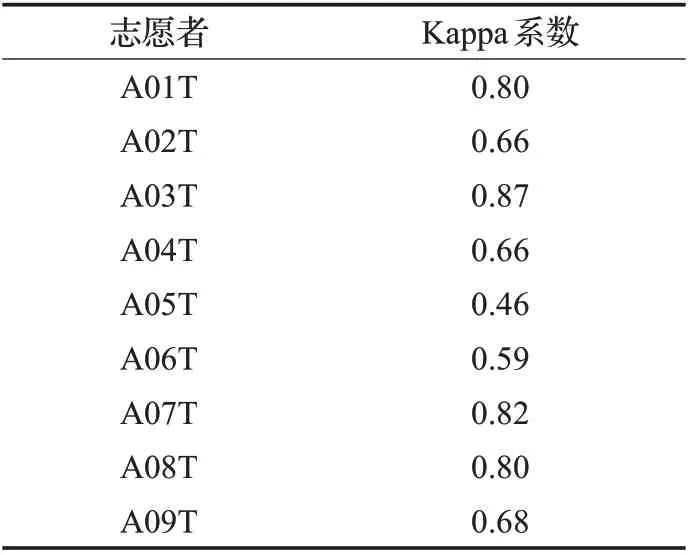
表4 9位志愿者的Kappa系数Table 4 Kappa coefficient of 9 subjects

将特征融合算法结合CNN分类器得到的分类结果与文献[11]、[22]和[23]进行比较，文献[11]使用带通滤波器去除噪声进行预处理在通过CSP滤波提取特征，最后使用HSS-ELM 进行分类；文献[22]在带通滤波预处理后，采用小波分析，使用CSP进行一级特征提取，再通过HT 变换进行二级特征提取，然后使用归一化和算数求和进行终极特征提取，最后使用PSO-SVM 分类；文献[23]使用孪生神经网络对脑电信号进行分类。具体如表5所示。

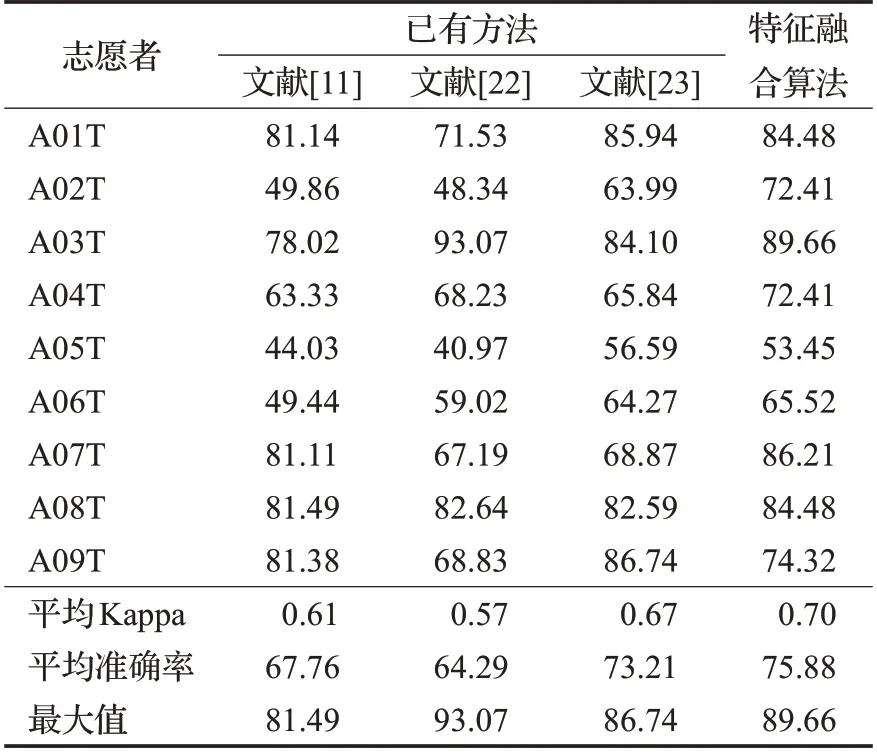
表5 与已有方法分类准确率的比较Table 5 Comparison with classification accuracy of existing methods%

由表5分析可知，文献[11]仅A09T的准确率高于本研究算法；而文献[22]也只有A03T 的准确率高于所提出的算法；对于文献[23]而言，虽然A01T、A05T、A09T高于特征融合算法，但A01T 和A05T 仅略高1.46 个百分点和3.14 个百分点，就整体而言结合CNN 分类器算法还是要优于文献[23]，且最大识别率为89.66%，仅次于文献[22]的最大识别率。由此可见，特征融合算法结合CNN分类器在提高多分类运动想象识别准确率上具有一定的优势。

5 结论

本文研究提出的运动想象EEG 信号特征融合算法，充分考虑脑电信号多个维度特征，利用小波包变换分析EEG信号的时频特点，通过共空间模式、希尔伯特-黄变换和非线性动力学算法进行特征提取，然后将不同维度的特征加权融合得到融合特征，相比于小波包变换和CSP 共空间模式组合的特征提取算法具有较高的准确率，再结合构建的CNN分类器，可进一步提高脑电信号的分类准确率。该算法分类准确率高、包含脑电信息多，取得了较为理想的结果。EEG信号多维度特征融合算法结合CNN 分类算法具有一定的优势，为运动想象的BCI 在特征提取和分类准确率提高等方面提供了理论基础和实验借鉴。