基于随机游走的图嵌入研究综述

腊志垚，钱育蓉，冷洪勇，顾天宇，张继元，李自臣

1.新疆大学 软件学院，乌鲁木齐 830046

2.新疆大学 新疆维吾尔自治区信号检测与处理重点实验室，乌鲁木齐 830046

3.北京理工大学 计算机学院，北京 100081

4.广东水利电力职业技术学院 大数据与人工智能学院，广州 510635

近年来，图结构信息在众多系统中都发挥着重要的支柱功能，图分析在计算机科学及相关应用领域中引起广泛的关注。图作为结构化知识库，不但能够协助更高效地保存和访问交互实体之间的关系知识，同时在现代机器学习任务中也起着重要的作用，机器学习任务使用图作为特征信息，来预测并发现新的模型。社交网络[1]、语言学[2]、生物学（蛋白质-蛋白质网络）[3]和推荐系统[4]——这些领域及更多相关领域的知识都很容易被建模为图，这些图可以捕捉单个单元（即节点）之间的交互（即边）。图有很多具体使用价值，例如：蛋白质作用分类、协作网络角色划分、社交网络用户推荐或预测药物分子治疗方向，图数据的使用会给各行各业带来巨大的价值。

从机器学习的角度来看，图数据分析面临的挑战在于图结构的高维非欧信息能否直接编码到低维的特征向量中。因此，基于图的机器学习的核心是找到一种将图结构的信息结合到机器学习模型中的方法[5]。传统的提取图结构信息的方法，主要是图统计（如：度或聚类系数）[6]、核函数[7]或通过精心设计的特征来提取局部邻域结构[8]，但设计这些特性是十分耗时且代价高昂的。由于上面的问题，一种新的学习编码图结构信息的表示学习方法（图嵌入）引起广泛的关注。这种表示学习方法很好地解决以前方法面临的困难，它和以前方法主要不同是如何处理表示图结构。其主要思想是通过学习一种映射关系，将图中的节点或整个（子）图映射为低维向量空间Rd中的点，通过不断的优化，确保嵌入空间向量最大程度的反应原始图结构。图嵌入向量直接作为下一步机器学习任务的特征输入，即图嵌入跳过图数据预处理的步骤，直接可以把图的预处理作为机器学习任务本身。

随着图嵌入技术的发展，随机游走被用来表示图中的属性，例如节点中心性[9]和相似性[10]。当只能观察部分图或图太大而无法整体测量时，该类型的方法是特别有用的。该类方法不仅帮助捕获网络中的社区结构，还可以通过迭代的方式适应图的微小变化。本文重点介绍基于随机游走的图嵌入研究方法，通过随机游走的方式，它把有复杂结构信息的图数据，提取成类似于语句序列的节点序列，其后基于语义分析的方法就可以用于图嵌入向量的生成。虽然基于随机游走的图嵌入方法只是图嵌入中的一类，但却是最经典的方法。

1 符号与基本定义

下面定义几个相关概念，类似于Wang等[11]的定义。

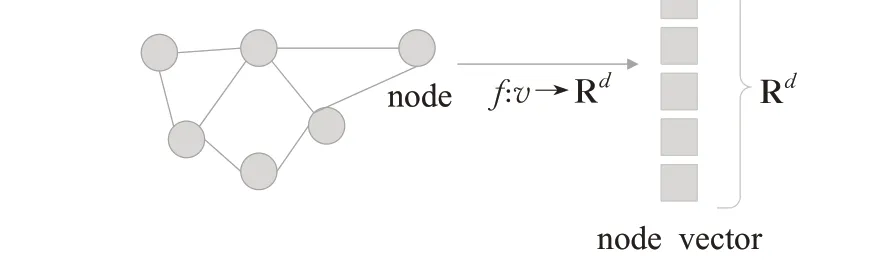
图1 图嵌入通用框架Fig.1 General framework for graph embedding

定义2（相似度）边的权重sij=wij，也称为节点vi和节点vj的一阶相似度，它也是节点之间相似度的首要度量指标。若节点vi和节点vj拥有相似的一阶相似度，就称节点vi和节点vj拥有二阶相似度。二阶相似度描述的是节点之间的领域结构的相似度。

定义3（信息网络[12]）一个信息网络是一个有向图G=(V,E,Φ,Ψ)，其中V是一个点集，E∈V×V是一个边集，Φ:V→A和Ψ:E→R分别是节点和边的类型映射函数，当|A|>1 或者|R|>1，该网络称为异构信息网络（heterogeneous information network，HIN）；否则，它是一个同构信息网络。

定义5（元图[14]）元图是在给定的HIN 模式TG=(L,R) 上定义的有向无环图（directed acyclic graph，DAG）g=(N,M,ns,nt)，它只有一个源节点ns（即入度为0）和一个目的节点nt（即出度为0）。N是节点类型n∈L的集合，M是边类型m∈R的集合。

2 随机游走的图嵌入模型分类

基于随机游走的图嵌入算法是借鉴自然语言处理中的词-向量模型[15]，使用不同的随机游走策略生成随机游走的节点序列，形成语料库，然后再利用Skip-Gram模型[16]或其变种[17]，生成图的嵌入向量。基于随机游走的图嵌入模型有着不俗的表现，特别是当图规模十分巨大时，随机游走方法可以很好地保留图的结构特性，生成可以近似反应节点属性的嵌入向量。现有的基于随机游走的图嵌入模型主要分为两大类：基于经典随机游走的模型和基于属性游走的模型。

2.1 经典随机游走模型

经典的随机游走采用不同的游走策略在图上行走，形成节点序列，最后生成训练需要的语料库。这种方式生成的语料库，是同类型或不同类型的节点构成的序列集合，该类模型分为两类：同构网络的模型和异构网络的模型。本节重点介绍这两种网络中经典的基于随机游走图嵌入模型，其中前四个模型为同构网络经典模型；后三个模型为异构网络经典模型，最后总结对比该类方法中不同模型的特点。

2.1.1 DeepWalk模型

DeepWalk模型[18]是基于Word2Vec模型[15]提出的学习网络顶点潜在表示的方法，借鉴了语言建模算法的思想，利用随机游走算法生成自己的语料库，并将图中的节点视为自己的词汇表，再通过Skip-Gram 算法[16]最大化节点序列中窗口范围内节点的共现概率，然后将节点映射到嵌入向量空间。DeepWalk模型的目标函数为：

如图2 是DeepWalk 模型框架，在实际应用中，直接计算Pr(uk|Φ(vj))(uk∈V)的归一化因子的代价是昂贵的。因此，把顶点集转换为二叉树，为随机游走频繁节点分配较短的路径，可以进一步加快训练的过程。该模型在小型图和大型图的嵌入表示中都有不错的性能体现，但是该模型只适用于无权图，且只保留了图的二阶相似性，有限的节点序列长度也影响了获取图的全局信息的能力。

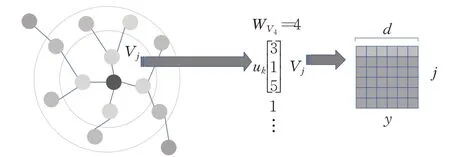
图2 DeepWalk模型结构Fig.2 Model framework of DeepWalk

2.1.2 Node2Vec模型

Node2Vec 模型[19]是在DeepWalk 模型的基础上，引进了一个有偏的随机游走的过程，在同质性和结构性[20]之间进行权衡，可以探索不同的邻域，最终保证生成的嵌入向量质量更高。Node2Vec模型的目标函数为：

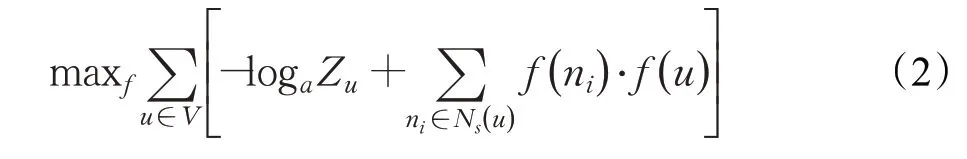
式中f:V→Rd是从节点到特征表示的映射函数。对于大型网络，每个节点划分函数Zu的计算成本太高，一般使用负采样对其进行近似[21]。但使用目标函数（2）还需要满足两条假设：条件独立性假设和特征空间对称性假设。

Node2Vec模型最大的特点就是设计有偏的随机游走策略，通过设置p和q两个参数来平衡广度优先搜索（breadth-first search，BFS）和深度优先搜索（depth-first search，DFS），来保证嵌入向量能够保持图结构的同质性和结构性，如图3 是Node2Vec 模型的转移策略。其中该算法在二阶随机游走中的转移概率为：

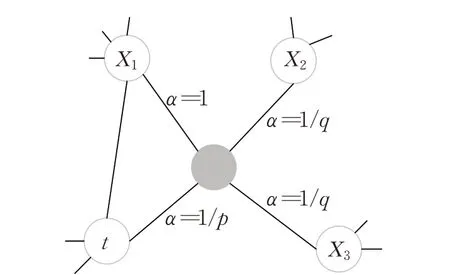
图3 Node2Vec模型转移策略Fig.3 Transfer strategy of Node2Vec model

此时，αp,q( )t,x的取值由p和q确定。虽然有偏的随机游走能帮助保存更多的图的结构信息，但对于图的全局信息的捕获能力仍有待提高。

2.1.3 WalkLets模型

DeepWalk 模型和Node2Vec 模型通过随机游走的方式把不同距离的节点连接起来，然后生成多个随机游走序列来隐式的保持节点之间的高阶相似度。Walk-Lets模型[22]将显式建模的思想与随机游走相结合，显式地编码多尺度顶点关系，该模型设计了多跳的方式来改变随机游走的策略，游走时跳过图中的一些节点，这样生成的随机游走序列集可以直接用于DeepWalk的模型上训练。WalkLets模型的目标函数为：

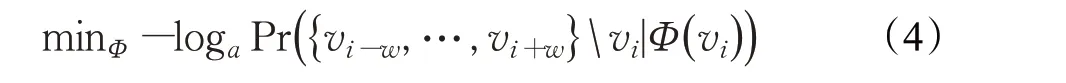
为了解决该模型多跳计算复杂度的问题，就需要忽略相邻节点之间的顺序，通过一个节点预测其局部结构，而不是使用上下文来预测缺失的节点。

该模型采用WalkLets模型使用了DeepWalk模型的嵌入向量处理的方法，但采用了不同于DeepWalk 模型的游走方式，每次跳过k−1 个节点，可以帮助捕获更远距离的图的信息。相比于DeepWalk 模型，该模型可以捕获节点和社区之间不同尺度的信息，生成更丰富的节点序列，建模节点多尺度的信息。

2.1.4 HARP模型

DeepWalk 模型和Node2Vec 模型使用短随机游动来探索节点的局部邻域，而忽略了长距离的全局关系，且这两种模型使用随机梯度下降的方式解决非凸优化的问题，该策略可能会陷入局部最优解。HARP（hierarchical representation learning for network）模型[23]通过更好的权重初始化来改进方案并避免局部最优解，该模型主要分为三部分：图粗粒度化、图嵌入和表示提升。HARP 模型通过图粗粒度化递归地合并原始图中的节点和边，获得一系列具有相似结构的较小图；然后，生成粗粒度化的节点嵌入；再通过层次结构传播和优化嵌入，不断的优化原图的嵌入。该算法的核心是图的粗粒度化，目的是降低图的规模同时保持图的基本结构，这一部分主要分为两个技巧：边塌陷和星状塌陷。

（2）星状塌陷：大部分真实的网络是无标度网络，这时，使用边塌陷效果不明显。所以HARP模型采用了星状塌陷的方式，就把共同以中心点为邻居的节点两两进行合并，这样也保证了图结构的二阶相似度。

因此，HARP 可以作为一种通用的元策略，用于改进随机游走方法的路径，获取更好的目标函数解。但是这种粗粒度的方式也会损失一部分图的结构信息，可能会导致生成的嵌入向量的精确度下降。

2.1.5 metapath2vec和metapath2vec++模型

前面的方法都是对同构网络的嵌入，没有考虑到现实中异构网络，针对异构网络多类型节点和链接的存在，Dong 等[13]提出一种用于异构信息网络的顶点嵌入方法，其中包含两个可伸缩的表示学习模型metapath2vec 和metapath2vec++，metapath2vec 模型利用元路径（meta-path）随机游走构建节点的异构邻域，然后再利用Skip-Gram模型建模结构和语义相近的节点，完成节点嵌入。metapath2vec模型通过在顶点v的领域Nt(v),t∈Tv最大化条件概率来学习异构网络G=(V,E,T)上的顶点特征：

式中，Vt是网络中t类型的顶点集合。在此过程中，metapath2vec++模型为Skip-Gram模型输出层中的每种类型的邻域指定一组多项式分布，而在metapath2vec，DeepWalk和node2vec中，Skip-Gram模型输出多项式分布的维度等于整个网络中顶点的数目。然而，对于metapath2vec++的Skip-Gram 模型，其针对特定类型的输出多项式的维度取决于网络中当前类型顶点的数目。最终可得到如下的目标函数：

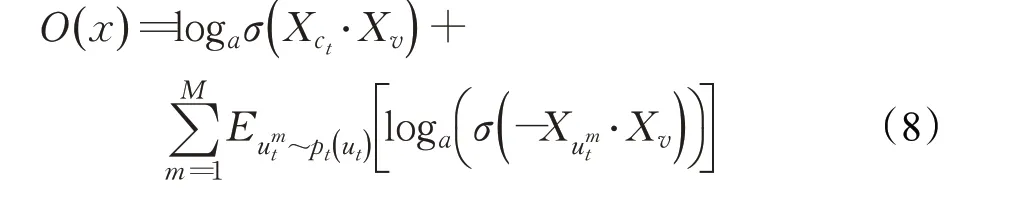
因此，metapath2vec++模型进一步支持异构网络中结构和语义关联的同时建模。

2.1.6 HIN2Vec模型

上述模型工作大多落脚于同构网络，而且往往只关注节点之间的整合关系或者限制类型之间的关系。针对这种情况，Fu 等[14]提出了HIN2Vec 模型，旨在通过利用节点之间不同类型的关系来捕获HINs 中丰富的语义。由于不同的元路径可能有不同的语义信息，所以作者认为对嵌入在元路径和整个网络结构中的丰富信息进行编码，有助于学习更有意义的表示。HIN2Vec模型主要分为两个部分：基于随机游走的数据生成和表示学习。第一部分工作是利用随机游走与负采样技术相结合，生成用于表示学习的数据；第二部分表示学习的核心是一个神经网络模型，学习表示向量的办法是最大化预测节点之间关系的可能性。因此，HIN2Vec模型保留了更多的上下文信息，不仅假设存在关系的两个节点是相关的，而且还区分节点之间的不同关系，并通过共同学习关系向量区别对待。HIN2Vec模型的目标函数为：

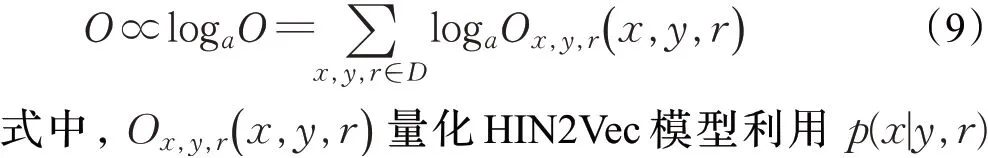
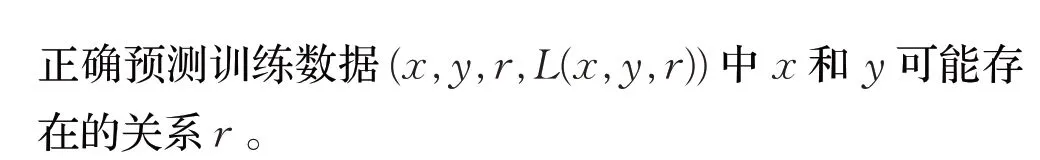
HIN2Vec 模型通过多任务学方法表示节点和关系的表示向量，把不同关系的丰富信息和整体网络结构联合嵌入到节点向量中。但是对于一个复杂网络来说，确定两个节点之间的所有关系是非常困难的。因此，为了简化这个问题，把预测两个节点之间的关系转换为二分类问题，即给定两个节点x、y，预测它们之间的关系r是否存在。

2.1.7 MetaGraph2Vec模型

异构信息网络（HIN）中的网络嵌入是一项具有挑战性的任务，因为不同节点类型的复杂性和节点之间丰富的关系。前面提出的方法大多是基于元路径的来描述HIN中的关系，但却不能很好地捕获节点之间丰富的上下文语义信息，针对这种情况，提出了一个新的元图概念，以捕获更丰富的结构、上下文和语义之间的远程节点。然后在此基础上提出了一种新的嵌入学习算法，即MetaGraph2Vec，它使用Metagraph 来指导随机游走的生成，并学习多类型异构信息网络节点的潜在嵌入。MetaGraph2Vec模型的嵌入函数为：

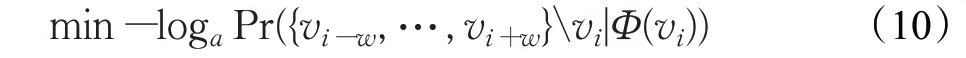
在Φ(vi)已知的条件下，最大化vi的上下文节点在w窗口大小内出现的概率，在模型实际的运算时，使用了负采样来近似目标函数，减少计算复杂度。

MetaGraph2Vec 模型的特点是在元图的随机游走，元图包含节点之间的多条路径，每条路径描述一种类型的关系，随机游走后便于捕获网络的上下文和语义信息。图4（a）显示了HIN的模式，该模式由3种节点类型组成：作者（A）、论文（P）和地点（V），以及3 种边缘类型：作者撰写论文、引用和发表。元路径P1:A →P →V →P →A 描述了两位作者在同一期刊发表论文的关系，而路径P2:A →P →A →P →A 描述两位作者有相同的合著者。而图4（b）构建了元图，它描述了两位作者在同一地点发表论文或共享同一合著者时的相关性，元图g可以被视为元路径P1和P2的并集，在生成随机游动序列时，它可以提供由P1和P2生成的随机游走的超集。

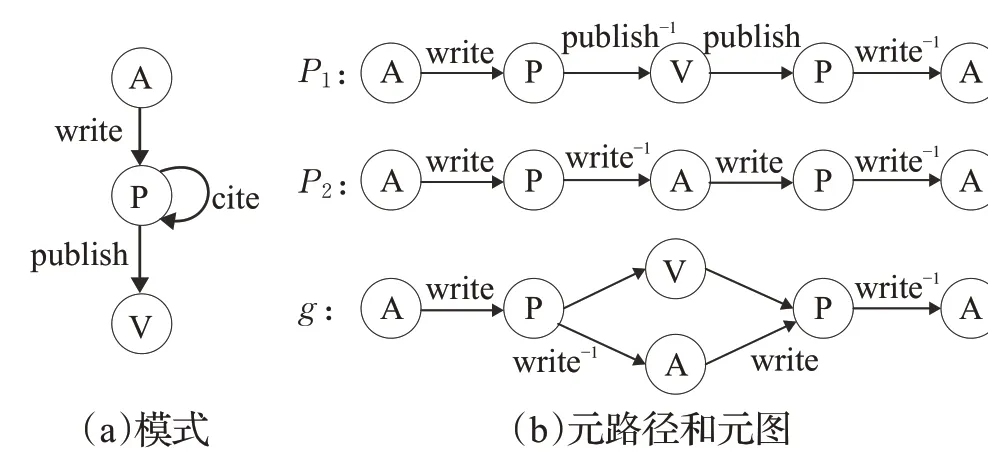
图4 模式、元路径和元图Fig.4 Schema，metapath and metagraph

该模型使用元图的方式，生成节点之间的多条路径，每条路径描述一种类型的关系，因此多条元路径的扩充提供有效的方法来捕获节点之间丰富的上下文和语义关系。这大大增强了基于元路径的嵌入技术处理非常稀疏异构信息网络的能力。

2.1.8 小结

同构网络中随机游走模型通过采用不同的随机游走策略，生成多样化的节点序列，可以反应更丰富的图结构信息。依此思路，2019 年，Schloetterer 等[27]提出了一种基于随机游走图嵌入的新扩展HALK（hierarchical random walk），从不同层次游动中移除一定百分比的最不频繁节点，实现更远节点之间的链接，反应更多的图结构信息。2021 年，Zhou 等[28]引入带重启的有偏随机游走的方法，提出了GEBRWR 模型来获得高精度的链路预测；Wu等[29]提出了ProbWalk算法，利用边缘权重确定转移概率，并根据转移概率生成用于图嵌入的随机游走序列。这一系列的方法，均取得了不错的实验效果。

而异构网络中随机游走模型更关注游走路径的选择，通过构建元路径或元图的方式来描述不同类型节点的特征和节点之间的关系，生成的节点序列可以更好的捕获结构、上下文和语义信息。从元路径的角度考虑，Shao 等[30]提出H2Rec（homogeneous and heterogeneous network embedding fusion for social recommendation）模型融合同质和异质信息，在同质信息网络使用随机游走策略中生成节点序列，在异质信息网络中利用元路径来引导随机游走方法生成节点序列。从构建元图的角度出发，文献[31]提出MIFHNE 模型，基于多源信息融合的异构网络，使用基于元图的随机游走策略捕获语义信息；文献[32]提出了复合元图（composite meta-graph，CMG），根据CMG 可以准确地阐述不同类型和不同距离的节点之间丰富的语义关系和丰富的结构上下文，然后提出了CMG2Vec（composite meta-graph based heterogeneous information network embedding approach）模型。这两种角度的考虑，均在异构网络的图嵌入中表现出了优良的性能。依据上面的模型介绍，如表1从类别、模型、年份、模型策略、优缺点和应用场景多个方面进行了总结。

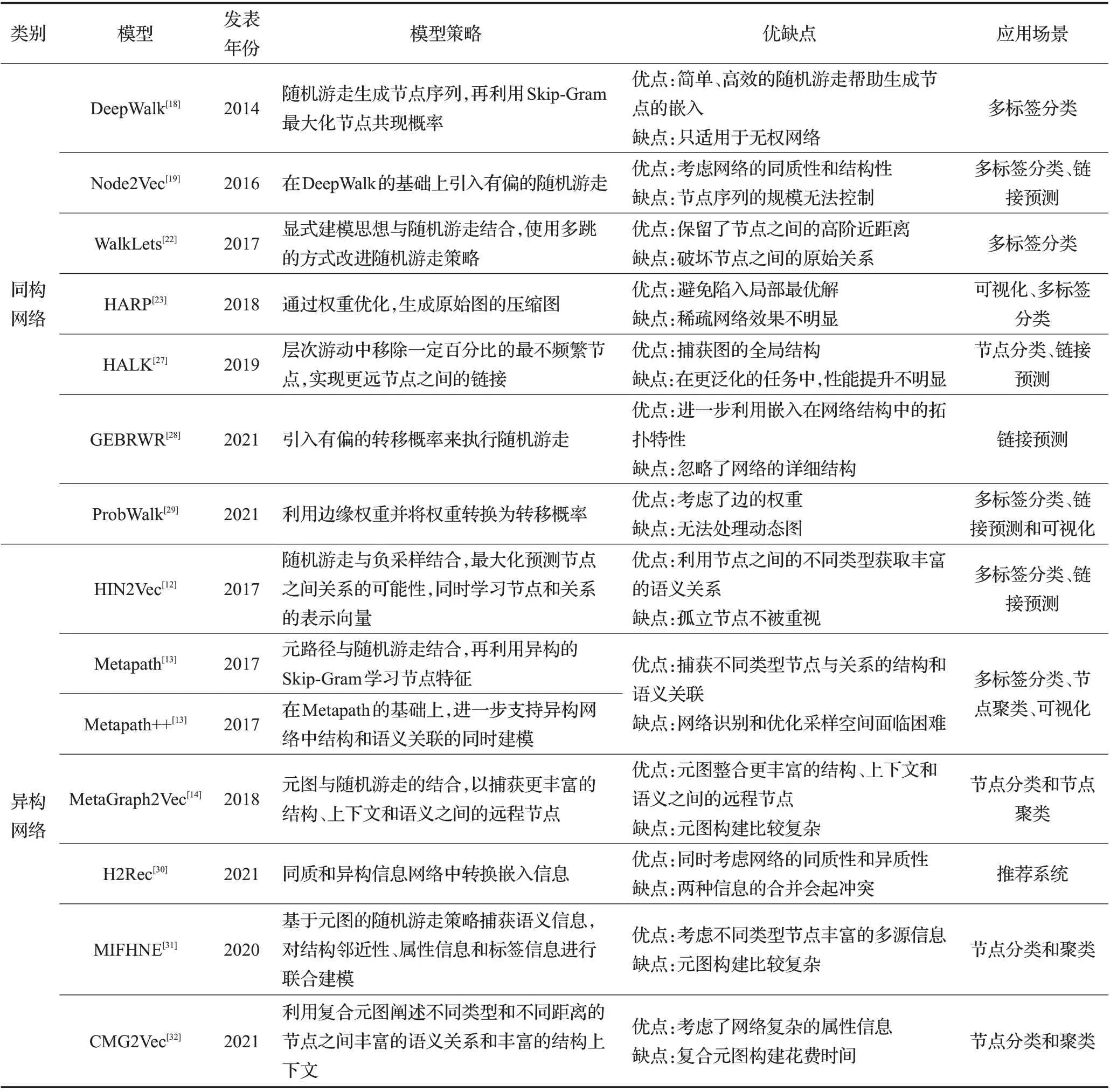
表1 经典随机游走模型对比Table 1 Comparison of classical random walk models

2.2 属性游走模型

经典的随机游走模型被广泛的应用在图分析的各种任务中，利用这些经典的模型生成节点的结构化序列，不仅可以捕获图的拓扑结构，且缓解了知识表示面临的稀疏性和维度灾难问题[33]。大量的事实表明，现实世界的网络中包含着丰富的信息，而不只是包含纯节点。基于属性游走的模型尝试把这些复杂信息抽象成属性，但是属性网络大多是异构的，且考虑属性会使节点交互变得更加复杂，增加模型建立的难度。为了解决这一问题，许多学者尝试在属性网络上执行随机游走，并利用它们进行网络节点的表示学习。

2.2.1 TriDNR模型

信息网络挖掘通常需要检查节点之间的链接关系以进行分析，基于传统随机游走的方法只关注节点本身，而忽略了节点的信息，但是大多数现实的网络蕴含着大量的信息。面对这种问题，2016年，Pan等[34]提出了一种三方深度网络表示模型：TriDNR模型，它使用来自三方的信息：节点结构、节点内容和节点标签，来共同学习最佳的节点表示。TriDNR 模型主要包含两个步骤：（1）随机游走序列生成，使用网络结构作为输入，并在节点上随机生成一组游动；（2）耦合神经网络模型学习，通过考虑以下信息将每个节点嵌入到连续空间中：随机游走语料库、节点内容相关性和标签信息。此时TriDNR模型的目标函数：

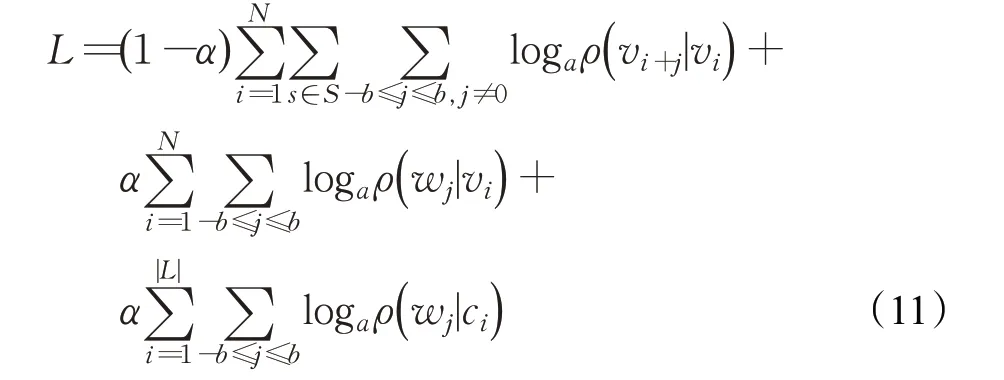
式中，α是平衡网络结构、内容和标签信息的权重，b是序列的窗口大小，wj表示上下文窗口的第j个单词。

如图5所示，DeepWalk方法仅基于网络结构学习网络表示，而TriDNR 方法耦合两个神经网络，从三方面（即节点结构、节点内容和节点标签）学习表示，以捕获节点间、节点词和标签词关系。耦合神经网络模型架构如图5右边框架所示，具有以下特性。

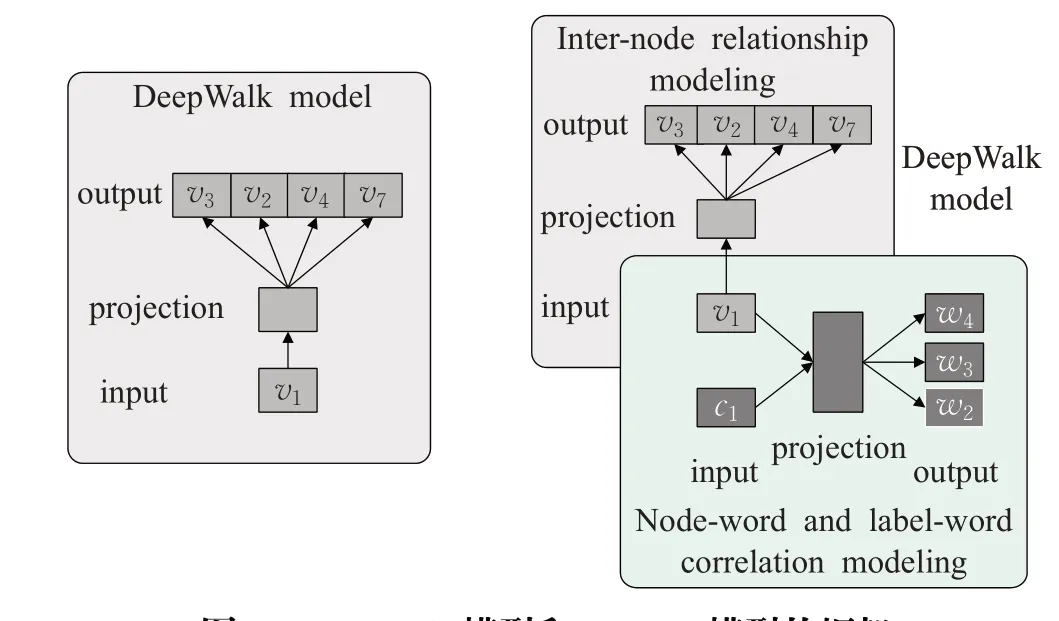
图5 DeepWalk模型和TriDNR模型的框架Fig.5 Architecture of DeepWalk model and TriDNR model

（1）节点间关系建模：TriDNR的上层可以从随机游走序列中学习结构关系。

（2）节点内容相关性评估：TriDNR的下层对文档中单词的上下文信息（节点内容关联）进行建模。

（3）连接：通过模型中的节点v1耦合这两层，表明v1同时受随机游走序列和节点内容信息的影响。

（4）标签内容对应建模：为了利用每个节点有价值的类标签信息，同时学习输入标签向量和输出单词向量，用于节点标签和节点内容之间的直接建模。

2.2.2 Role2Vec模型

图嵌入中，使用传统的随机游走主要捕获顶点之间的接近度[35]，从而使图中彼此接近的顶点嵌入在一起，也就是说随机游走可能首先访问附近的顶点，这使得它们适合于寻找社区，而不是角色（结构相似性）。2019年，Ahmed 等[36]提出了Role2Vec 模型，利用属性随机游走的灵活概念来解决此问题，并作为推广现有方法的基础，如DeepWalk、Node2Vec和许多其他利用随机游走的方法，该框架使这些方法能够更广泛地适用于转换学习和归纳学习，且可用于属性图。Role2Vec模型认为两个顶点在属性或结构特征方面相似，则它们属于同一集合，而顶点属性和结构特征可以通过根据其端点的类型区分来表示，这引出了属性随机游走的概念，因此属性游走是相邻顶点类型的序列，该定义诱导顶点类型序列称为属性随机游动，也是一个马尔可夫链。因此，Role2Vec模型的目标函数：

Role2vec 框架使用顶点映射和属性随机游走来学习嵌入。因此，本模型的目标是对每个顶点类型与其上下文类型相关的条件概率进行建模，嵌入结构（即嵌入和上下文向量）在具有相同顶点类型的顶点之间共享。要注意：Role2vec 模型学习聚合网络的嵌入，是把单个顶点之间的详细关系聚合为顶点类型之间的总关系。

2.2.3 GraphRNA模型

在现实系统中，节点不会是纯顶点，还具有不同的特征，这些特征由丰富数据集来描述。这些节点属性包含丰富的信息，这些信息通常补充了网络，并为基于随机游走的分析带来了机会。然而，目前尚不清楚如何为属性网络开发随机游动，以实现有效的联合信息提取，并且节点的属性信息使网络的结构变得更加复杂。为了弥补这一差距，2019 年，Huang 等[33]提出了GraphRNA 模型，该框架是一种新的基于属性的网络嵌入框架，将协作游走机制AttriWalk 与图递归网络GRN 结合，在属性网络上更有效地学习节点的表示。GraphRNA可以在无监督、有监督或半监督的环境下进行训练，这个属性是从GCN[38-39]继承的。GraphRNA 模型可大致分成三部分：（1）统一的游走机制，为了实现对复杂的属性节点采样的目的，构建基于节点属性的二部图，帮助生成多样化的节点序列；（2）图递归网络（GRN），一种有效帮助节点表示的深层结构，生成的隐藏状态序列符合采样节点之间的交互关系；（3）生成节点嵌入，选取部分以某节点为起始节点的序列，构建集合，然后利用池化方法来生成节点的嵌入向量。该文以有监督的环境为例，基于交叉熵误差，目标函数可定义如下：

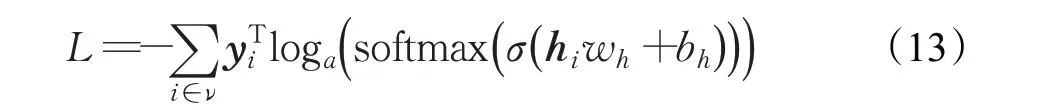
式中，yi是定义了节点i标签的one-hot 向量，wh是一个权重网络，其每一行wj对应于节点属性类别的潜在表示，hi是利用属性随机游走生成的节点序列再经过GRN后生成的节点i的表示向量。

该模型解决向高度节点收敛的方式是构建节点属性的二部网络，增加随机游走多样性，设置一个概率参数来决定随机游走的采样策略：在二部图网络上走两步，或在局部拓扑网络上走一步，最后生成节点序列来反应节点之间的复杂的属性交互。在二部图g(υ,μ,ε)的游走增加了属性游走的多样性和灵活性。

2.2.4 FEATHER模型

现实网络中邻域特征的解释可能很复杂，网络中包含多个属性，具有影响节点和网络特性的各种分布。因此，简单线性聚合，如平均值，并不代表这种多样性信息。针对这种情况，2020 年，Rozemberczki 等[40]提出了FEATHER 模型，使用了一个灵活定义在图顶点上的特征函数的概念来描述顶点特征在多尺度上的分布，这是一种计算效率很高的算法，其中特征函数的概率权重定义为随机游动的转移概率。FEATHER 模型的损失函数为：

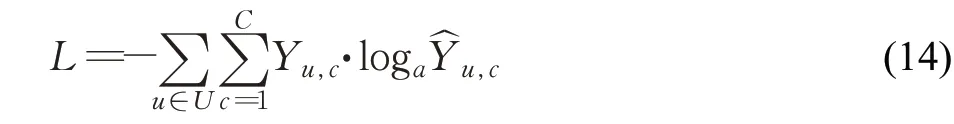
该损失通过梯度下降的方式，搜索β∈R(2⋅k⋅d⋅r)⋅C（分别有β0和β1）和Θ͂ 的最优值。其中Y=softmax(Z⋅β)，C是节点类的数量，Z是利用评估点向量Θ͂ ，归一化邻接矩阵和节点特征作为输入的图神经网络的前向传递；Ŷ=softmax(σ(Z⋅β0)⋅β1)，这里β0∈R(2⋅k⋅d⋅r)⋅h是训练的输入权重矩阵，β1∈Rh⋅C输出权重矩阵，h是隐藏层神经元个数。FEATHER 模型的核心是特征函数的概念，一个有属性的无向图G=(V,E)，G的节点具有随机变量X描述的特征。源节点u在特征函数求值点θ∈R处的特征函数定义如下（其中i表示虚单位）：

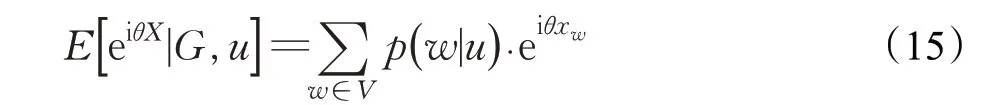
其中，从属概率p(w|u)描述源节点u和目标节点w∈V之间关系的强度，源节点u和目标节点w不必直接连接。

FEATHER模型可以在线性时间内高效地计算大型属性图上的特征函数，创建节点的欧氏向量空间表示。FEATHER 模型对数据损坏具有鲁棒性，并且同构图具有相同的向量空间表示，能高效、稳健地将知识从一个图转移到另一个图。

2.2.5 小结

基于属性游走的模型不仅关注网络中的节点和拓扑结构，还关注节点本身多样化的信息。随机游走的过程中，把网络中的信息抽象成属性，生成带有属性的节点序列；图嵌入向量生成的过程中，使用属性节点序列更有利于网络的表示。大量事实表明捕获多尺度上的属性邻域关系对于一系列应用非常有用，MUSAE 模型[41]从节点周围的节点属性的局部分布中捕获节点的信息，融合了属性化和邻近保持算法的优点。现有的属性网络嵌入模型利用浅层网络来获取网络的特征信息，但却无法捕获属性网络中非线性的深层特征，这样必然会导致结果陷入局部最优解。针对这种情况，Hong等[42]提出一种深度属性网络嵌入框架，采用个性化随机游走的模型来捕获网络结构和节点属性之间的相互作用，来捕获网络中的复杂结构和属性信息。研究人同的工作，均证明基于属性游走的图嵌入模型有着旺盛的生命力。依据上面的介绍，表2 从模型、年份、模型策略、优缺点和应用场景多个方面进行总结。

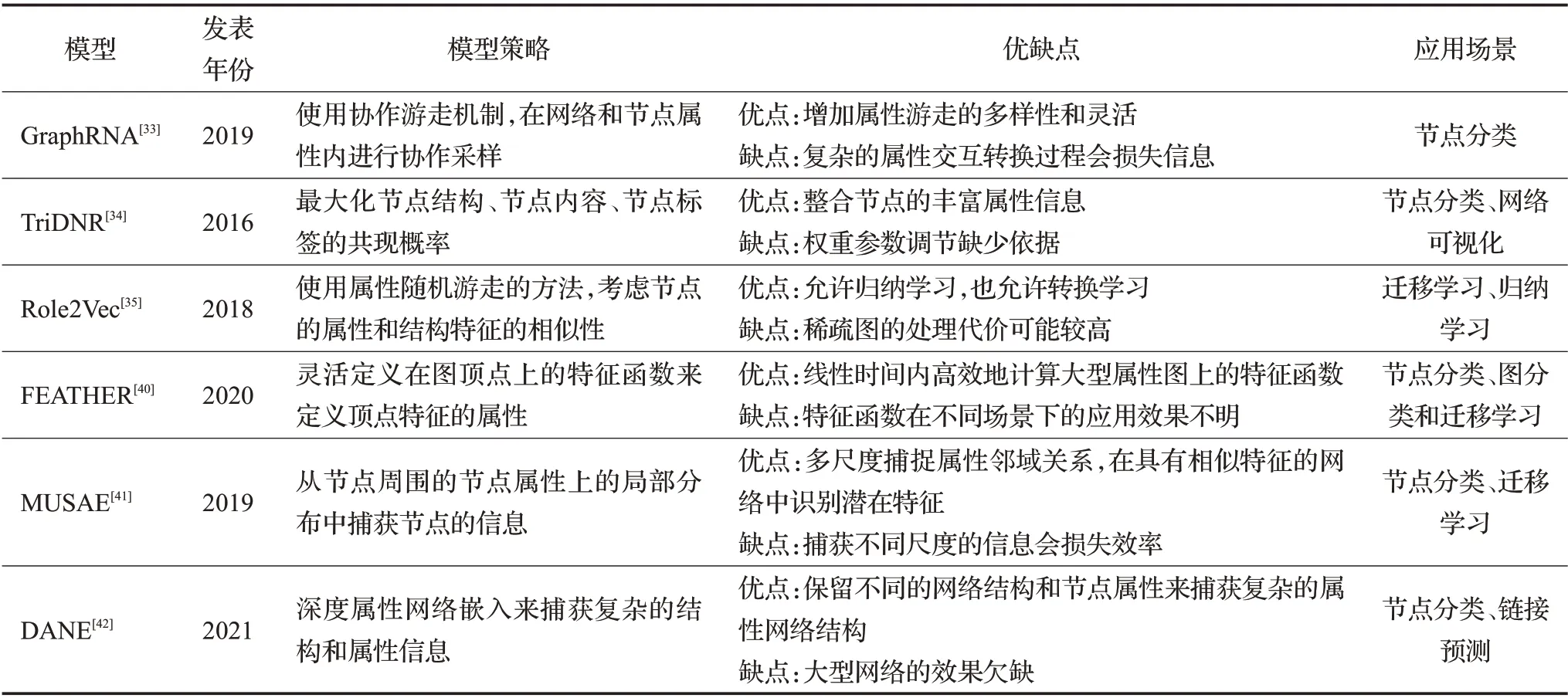
表2 属性游走模型对比Table 2 Comparison of attribute walk models

2.3 方法小结

本章主要介绍两大类基于随机游走的图嵌入模型。基于经典随机游走的模型又分为两小类：同构网络模型和异构网络模型，同构网络节点或边的类型只有一种，而异构网络会有多种类型的节点和边，因此异构网络的模型更加复杂一点；后面介绍基于属性游走的图嵌入模型更加复杂，因为网络属性包含多个维度的属性信息。总体来看，同构网络模型更关注随机游走的策略，异构网络模型更关注游走路径的构建，而最后的属性游走模型在前面工作的基础上，还关注节点本身多样化的信息。依据已有的成果对各种方法进行分析，表3从类别、机制、解决问题、优势、局限性和适用场景多个方面，对基于随机游走的图嵌入模型进行总的特征分析。

表3 基于随机游走的图嵌入模型对比Table 3 Comparison of graph embedding models based on random walk

3 图嵌入算法实验对比分析

基于随机游走的图嵌入研究具有多种不同的类型，对于不同类型的图嵌入应用需要选择不同的数据集和评价指标。本实验主要利用同构网络数据集，进行实验的对比与分析。

3.1 数据集

本实验使用的数据集有：Karate[43]、Football[44]、Dolphins[45]、Hep-th[46]、Astro-ph[47]、Cond-mat-2005[48]，表4对这些数据集的特点和特征，进行相关的总结。

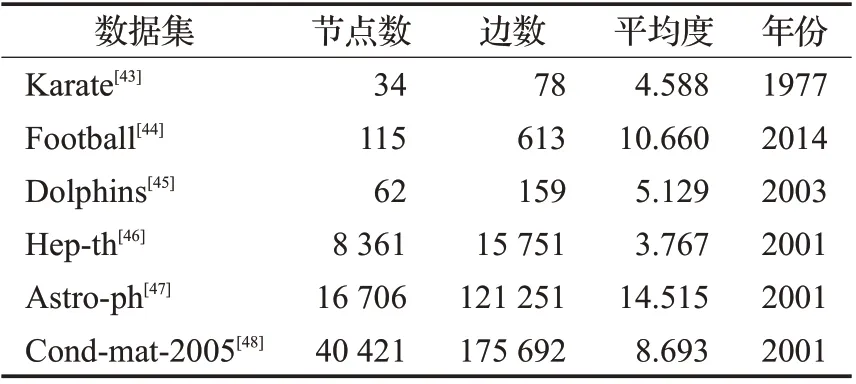
表4 实验数据集Table 4 Experimental datasets

3.2 实验分析

3.2.1 网络重构

网络重构任务是利用学习到的低维嵌入来重构图的边和拓扑结构，用于评估嵌入向量的质量。嵌入作为图的低维表示，可以帮助重建图。对于每种方法生成的图嵌入向量，重建节点之间的链接，然后使用前k对顶点的预测链接所占原始图中链接的比例来评估模型的重构表现。网络重构任务通常采用MAP（mean average precision）[49]作为评价指标：

网络重构帮助理解图嵌入的性能，好的网络嵌入会有优良的性能指标的体现。在Karate、Football、Dolphins、Hep-th、Astro-ph和Cond-mat-2005数据集上，做了Deep-Walk、Node2Vec、WalkLets 和Role2Vec 这4 种模型的不同维度嵌入向量指标对比。从图6（d代表嵌入向量空间维度大小）的实验结果来看，总体上4 种模型都随着嵌入向量维度的增加有更好的指标体现，前3种数据集从规模来看，相对规模比较小，随着维度的增加，性能指标相对处于平滑状态，而另外3 种数据集的规模比较大，随着维度的增加，性能指标也相应递增，可见更高的维度有助于保存更多的网络信息；从图中也可以看出DeepWalk、Node2Vec 和WalkLets 这3 种模型的性能体现优于Role2Vec模型，而Role2Vec模型在这6种数据集上表现性能比较差且不稳定，原因是网络重构更关注的是网络邻近节点的链接，也就是社区结构，前3 种模型关注网络的邻近节点，即关注节点的一阶相似性，而Role2Vec模型不只关注网络中节点的属性，更关注网络中节点的结构相似性，因此对于节点之间的邻近链接的表征就不够好。

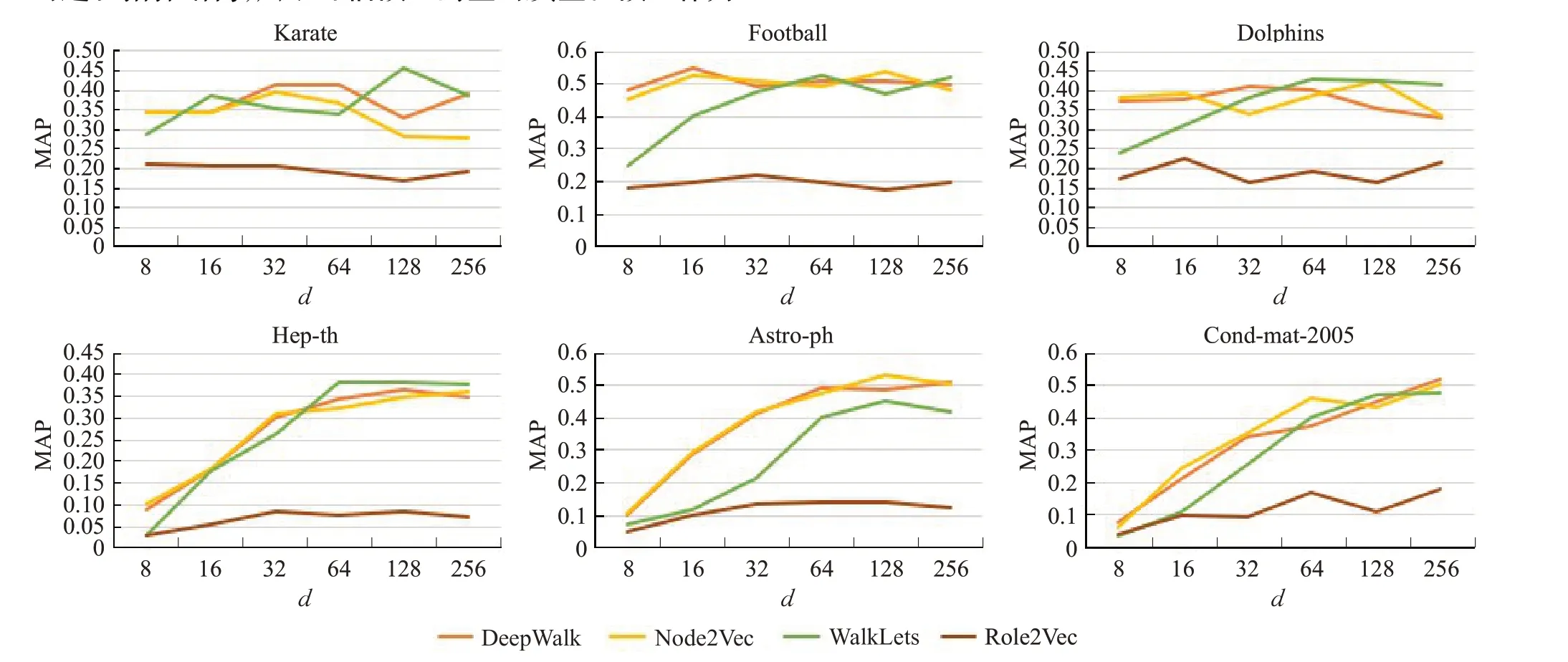
图6 网络重构性能对比Fig.6 Comparison of network reconstruction performance

3.2.2 可视化

可视化任务是对生成的嵌入向量在二维空间展示，便于直观地观察原始图的特点和拓扑结构。如果可视化的数据集是有标签的，一个好的嵌入可以使标签相同的节点彼此接近，不同的标签节点彼此远离。在Karate 数据集上做DeepWalk、Node2Vec、WalkLets和Role2Vec 模型的可视化对比，如图7 所示，学习4 种模型的128 维的嵌入向量，并将其输入到t-SNE[50]以将维度减少到2，然后在二维空间中可视化节点。利用网络中节点的标签和社区结构，可以直观地看出4 种模型都能较好地保留原始图的结构，相对来说，前3 种模型可以有效地捕捉节点的社区结构，使同类型的节点更近；而Role2Vec 模型未能充分地利用节点的特征和标签信息，导致模型的性能较差，同类型的节点分布零散。

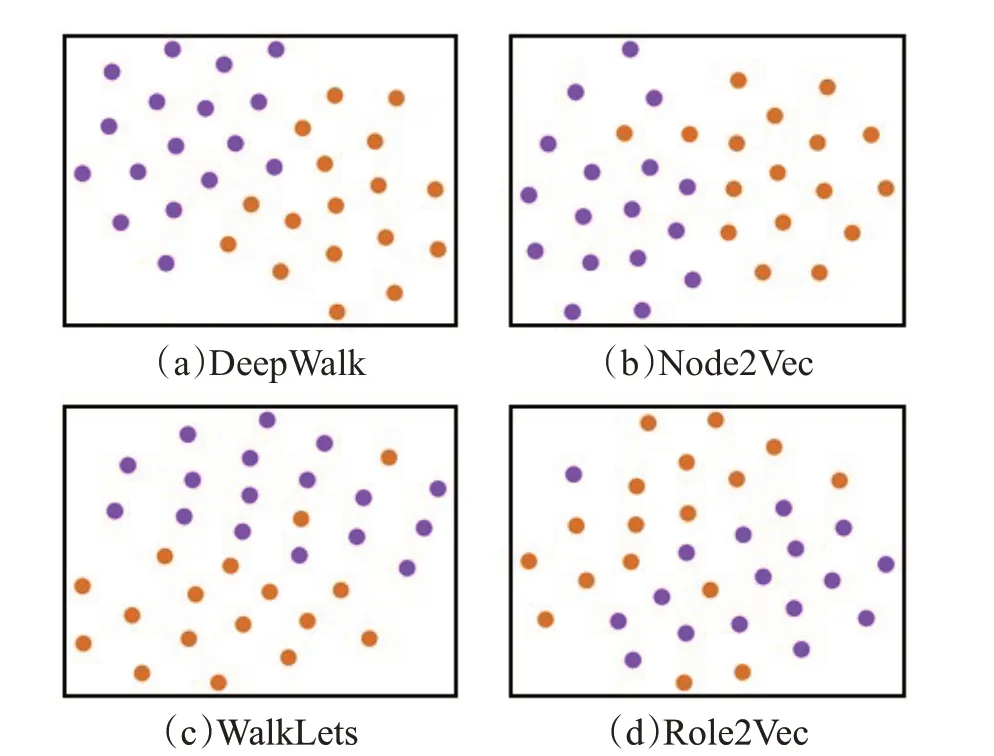
图7 可视化性能对比Fig.7 Comparison of visualization performance

4 研究展望

本文主要介绍基于随机游走的图嵌入方法和应用，比较了各种模型之间的差异，对基于随机游走图嵌入的方法进行了比较全面的阐述。图上机器学习的表示学习方法为传统特征工程提供了一种强有力的替代方法，基于随机游走的图嵌入用于图数据的表示，可以用于不同的任务，这些任务可以大致分为：网络重构[51-52]、节点分类[53-54]、图聚类[55-56]、异常点检测[57]、链接预测[58]和可视化[59]。虽然基于随机游走的图嵌入实现了数据的降维和表示，在解决图数据稀疏问题、计算效率低和图数据理解等方面表现优异，但是基于随机游走的图嵌入也面临着一些亟待解决的问题。

（1）属性选择：实际应用场景下图数据不仅仅包含单纯的节点，还含有复杂的属性和拓扑结构。图嵌入向量不仅需要保留图的节点，还要能够保留图的属性。因此，需要考虑选择合适的距离度量和属性，保证嵌入向量的性能。

（2）可扩展性：现实的世界中存在着复杂的网络结构，因为网络的千差万别，需要寻找一种普适性的办法，保留网络的全局属性。因此，考虑嵌入方法的可扩展性也是一个亟待解决的问题。

（3）嵌入维数：真实的场景下节点数量和链接千差万别，因此针对不同的数据集选取不同的嵌入维度反应网络的特征，是一件很有技巧的事情。若是一味地使用高的维度，会导致较高的时间和空间复杂度。

（4）可解释性：表征学习之所以有吸引力，是因为它减轻了手工设计特性的负担，但它也以众所周知的可解释性为代价。基于嵌入的方法提供了最先进的性能，但是这些算法的基本限制以及可能的潜在偏差相对未知。为了向前发展，必须注意开发新的技术来提高所学表示的可解释性。

随着大数据技术的发展，呈现出海量、高维、稀疏、动态和异构等复杂特征的图数据或图结构，给图数据的分析和挖掘带来了巨大的挑战。基于随机游走的图嵌入模型虽然在各种任务中表现出不错的性能，但是它也面临着一些挑战，如：节点海量性、属性信息融合、图的异构性、节点的动态变化性和模型的非线性。图上机器学习的表示学习方法为传统特征工程提供了一种强有力的替代方法，然而，在改进这些方法的性能方面，更重要的是建立一致的理论框架，为后面的研究提供可参考的标准。总体来说，接下来的研究方向分为以下几类：

（1）面向超大规模网络的嵌入模型。虽然基于随机游走的模型可以较好地反应大型图的网络信息，但生成嵌入向量的代价较高。随着社交媒体和电商的发展，网络中节点和边的数量级一定会越来越大，在这种背景下，提高嵌入模型的性能和降低网络生成的代价是生成超大规模图嵌入向量亟待解决的问题。

（2）面向复杂网络的嵌入模型。复杂网络不只是同构网络，它还可能是异构网络，且网络中包含有复杂的属性信息。针对不同类型的复杂网络，设计不同的策略来反应网络中复杂的信息和拓扑结构，也是很有前景的一个研究方向。

（3）面向动态网络的嵌入模型。大部分场景下图是动态演化的，这个演化过程包含着复杂的信息。随机游走的方法不断迭代的过程可以反应图动态演化过程中的微小变化，设计合适的游走策略在降低时间复杂度的同时，还保留动态图的演化信息，是动态图嵌入必须要考虑的内容。

（4）面向特定场景的嵌入模型。许多嵌入模型用于可视化、节点分类、链接预测和异常点检测等任务中都取得了不错的实验效果。但是真实的场景（推荐、反作弊等）提供了丰富的大规模的多样化的数据，不再只是对单一任务的要求，需要考虑不同类型的任务的结合，因此，研究特定场景下的图表征学习也是一个热门的研究方向。

5 结语

图表示学习（图嵌入）是人工智能研究的热点之一，随着图嵌入方法的不断发展，该研究吸引到了大量研究人员的关注。本文在介绍完背景知识后，重点介绍了基于随机游走的图嵌入方法，将该类型方法分为基于经典随机游走的模型和基于属性游走的模型，进行了深入的对比分析，并做了展望。