基于Fisher信息的室内主动SLAM

席永辉，胡士强

上海交通大学 航空航天学院，上海 200240

同时定位与地图创建（simultaneous localization and mapping，SLAM）是指机器人在未知的环境中，依靠自身携带的传感器完成自主定位与周围环境地图的创建[1]。近年来，基于视觉传感器的SLAM 在机器人和无人机的室内定位中得到了广泛的应用[2-4]。第一个实时的单目视觉SLAM系统[5]是在2007年提出的，前端跟踪稀疏的特征点，以扩展卡尔曼滤波为后端，实时更新相机的状态和路标点的位置，但是前端特征点容易跟丢，应用场景有限。同年，Klein 等人[6]提出了PTAM（parallel tracking and mapping），是第一个使用非线性优化的后端，并且实现了跟踪与地图创建的并行化，后续许多优秀的开源方案如Fast-SLAM[7]、ORB-SLAM2[8]都是在此基础上完成。然而，这些算法过度依赖环境的纹理信息，当遇到弱纹理的环境，会找不到足够多的匹配特征点，从而导致算法的精度降低甚至定位失败[9]。

针对弱纹理环境下特征缺失带来的问题，国内外的学者也做了大量的研究。李海丰等人[10]通过提取环境中的点、线、面特征，弥补环境中点特征不足带来的影响，但是匹配算法复杂，只适用于具有结构化的人造环境；Engel等人[11-12]利用直接法，直接对像素进行操作，不依赖纹理信息，但是算法容易受到光照变化的影响，相机不能运动过快，鲁棒性较弱。除了上述基于图像层面的研究方案，还有不少学者从系统结构的层面出发，引入惯性传感器去弥补视觉特征的缺失[13-14]，或者设计冗余结构，采用多位姿测量系统进行位姿估计[15]，但是前者在视觉特征长期缺失的情况下会产生较大的误差漂移，后者传感器的标定较难，系统结构庞大，不易于移植和维护。

不同于上述传统的视觉SLAM算法，越来越多的学者开始研究弱纹理环境下运动规划和位姿估计联合优化的主动SLAM算法[16-18]，但是，这类方法计算复杂度高或者需要事先知道环境中的特征点分布，对载体的机动性能也有一定的要求。考虑到Fisher信息[19]可作为衡量参数估计性能的定量指标，被广泛应用于特征点筛选[20]、最优化设计[21]等方面，本文针对弱纹理环境下的位姿估计问题提出了一种基于Fisher 信息的室内主动SLAM算法，对载体的运动轨迹和机动性能没有过多限制，主要贡献及创新性如下：

（1）提出了一种新的主动SLAM 框架，在ORBSLAM2 的基础上增加了Fisher 信息场构建模块与云台控制模块，算法能够将前端的特征跟踪状态反馈到云台相机控制中，在特征丢失时通过改变相机的观测方向，使得整个系统能够进行主动重定位，得到稳定且准确的结果。

（2）为了找到最优位姿估计对应的最优观测方向，理论上分析了Fisher信息与参数估计性能之间的关系，并推导了位姿估计中Fisher信息矩阵的计算公式。

（3）在Gazebo仿真平台中搭建了室内环境，将所提算法运用到四旋翼无人机的室内位姿估计中，验证了算法的有效性。

1 改进后系统框架

以四旋翼无人机为载体，改进后的系统框架大致可分为位姿估计、Fisher 信息场构建和云台控制这三个部分，具体框图如图1所示。

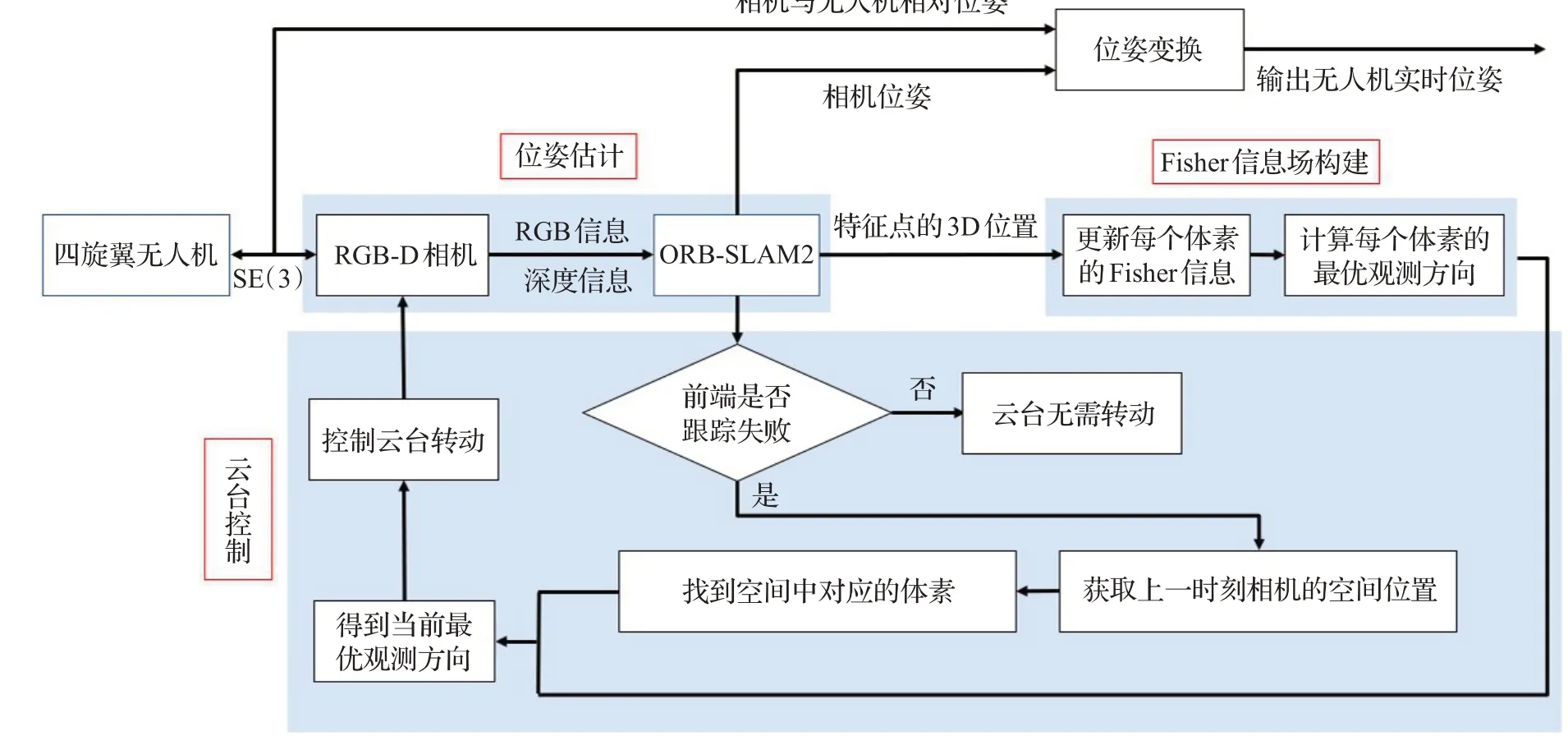
图1 改进后系统框架Fig.1 Overall architecture of improved system

位姿估计部分通过跟踪地图中的ORB[22]特征点，实现对相机位姿的实时估计；Fisher 信息场构建部分根据特征点的空间位置分布实时更新每个体素的Fisher信息并计算出最优的观测方向；云台控制部分在相机所获得的图像遇到弱纹理区域而跟踪失败时可以通过改变相机的观测方向来进行主动的重定位，增强了系统的鲁棒性。相机与无人机的相对位姿可以用一个三维的欧式变换SE（3）来表示，该变换随着云台的转动而改变，但是能直接获得，由位姿估计模块输出的相机位姿和相机相对于无人机的位姿可以得到无人机的六自由度位姿。每个部分的具体内容将在后续小节中详细介绍。

2 位姿估计

本文以ORB-SLAM2开源方案作为位姿估计模块，ORB-SLAM2是现代SLAM系统中较为完善易用的系统之一，许多研究工作都以其为标准，或者在它的基础上继续开发。ORB-SLAM2 支持单目相机、双目相机、RGB-D 相机3 种传感器形式，由于RGB-D 相机可以直接获取场景的深度，初始化简单，特征点的空间位置容易获得，所以本文采用RGB-D 深度相机作为视觉位姿估计的传感器。ORB-SLAM2 分为3 个并行的线程：跟踪线程，局部优化线程以及闭环检测线程。其中，跟踪线程将空间中的特征点和当前帧中的特征点进行匹配并投影到当前帧中，通过最小化重投影误差来实现相机位姿的极大似然估计：

ui表示观测的数据，即特征点在图像中的坐标，τ为相机坐标系（原点为相机的光心，x轴与y轴与图像的X、Y轴平行，z轴为相机光轴）到图像坐标系的投影函数，Pi表示特征点在世界坐标系（把最初的相机坐标系固定为世界坐标系）下的坐标，exp(ξ^)为李代数的指数映射[9]。为了减小累计误差，引入了局部优化和闭环检测线程，具体实现过程可以参考文献[8]，这里就不再赘述。

3 Fisher信息场构建

3.1 Fisher信息的概念

Fisher信息是用来度量含参随机变量所携带参数信息多寡的量。假设估计的参数为θ，观测数据x的分布依赖于参数θ，用P(x|θ)表示，参数θ的无偏估计为θ′，由无偏估计的定义可得：

由式（13）可知，从估计误差的角度来看，Fisher信息矩阵作为衡量参数估计性能的定量指标，给出了参数估计的精度上限，通过最大化Fisher信息矩阵的某一度量函数（常用矩阵的迹或者行列式）可以实现参数估计的协方差最小化[23]。

3.2 位姿估计中Fisher信息的计算

相机的位姿估计问题本质上也是一个参数估计问题，可以从以下3 个方面评价某个参数估计方法的性能：无偏性，指估计量的数学期望等于被估计参数的真实值；有效性，指无偏估计量的方差，方差越小的估计越有效；相合性，指当观测数据足够多时，估计值会逐渐收敛于真值。对于形如式（1）的极大似然估计来说，由极大似然估计的渐近正态分布性质可知其满足相合性，但是在有限样本的情况下，因为非线性误差的存在达不到无偏性，不过偏置量会随着Fisher信息的增大而减小[24]，另一方面，位姿估计的方差难以直接获得，但是由3.1节中Fisher 信息的性质可知，估计方差也会随着Fisher 信息的增大而减小，所以某个位置Fisher信息量最大的方向可作为相机的最优观测方向，以该方向进行观测，可以达到位姿估计无偏性与有效性的最大化。以下是位姿估计中Fisher信息的具体计算过程：

其中b为二值函数，当位姿为ξ的相机能观测到特征点Pi时取1，否则取0。

由于受到相机视场角的影响，即使在同一位置，不同观测方向的Fisher信息量也不一样，根据公式（24）可知，要计算某个位置Fisher 信息量最大的方向，需要在每个方向对所有特征点进行迭代，然而，实际过程中特征点数目往往是巨大的，会带来较大的计算量，无法满足实时性的要求，参考文献[25]的思想，用旋转矩阵Rwc和平移向量twc表示相机位姿，首先对相机的可观测模型进行如下近似：

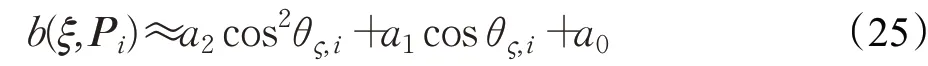
其中a0、a1、a2是对相机可观测模型进行近似后的参数，和相机的视场角有关，θς,i为相机光心到特征点Pi的射线与相机光轴正方向之间的夹角，它的余弦值为：

上式是一个带约束的非线性优化问题，可以使用序列二次规划算法（SQP）对其求解，将原问题转化为一系列二次规划子问题，经过数次迭代之后最终收敛到原问题的最优解[26]。

3.3 Fisher信息场

通过上述分析可知，Fisher 信息表征了观测量与被估计参数之间的内在联系，而对于特征点法的SLAM算法来说，相机在某个位姿的观测数据只和特征点的空间位置分布有关，故只需利用特征点的世界坐标更新该位姿的Fisher信息量。但是由于空间位置的连续性，不可能对每个位置都进行Fisher信息的计算，这时候需要把连续的空间离散化成若干个体素（即空间中的小立方体）。具体步骤如下：首先确定离散化后的体素数量，然后根据室内空间的大小和体素数量计算每个体素的边长，按照该边长把三维空间均匀分割，得到一系列的体素，最后用体素中心点处的Fisher信息代替整个体素内所有点的Fisher信息。在设置体素数量的时候，为了最大化空间降采样后的精度，希望在保证与原有算法具有相同运算效率的同时让体素的数量尽可能的多。假设体素的数量为Nv，计算一个特征点给一个体素带来的Fisher 信息需要的时间为t，特征点随着关键帧的插入而增加，关键帧插入的平均时间间隔为T，每次平均增加的特征点个数为Nf，那么在关键帧插入的时间间隔中，要完成每个体素Fisher 信息的更新，体素个数需要满足：

在本节中，暂不考虑实际的物理尺寸与运算效率，给出一个离线仿真的结果，把10×10×10 的三维空间等分为1 000 个体素（每个体素的大小为1×1×1），为了更加直观地显示效果，把200个特征点都随机分布在x=0的平面上，特征点的空间坐标已知，在Matlab 中进行仿真，得到的结果如图2所示。

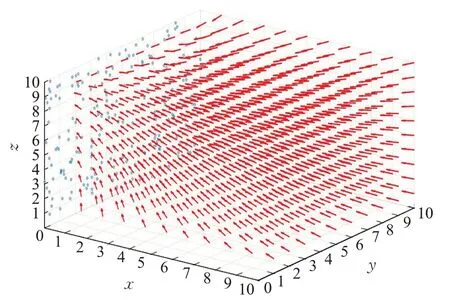
图2 Fisher信息场示意图Fig.2 Diagram of Fisher information field

图2中五角星代表空间中的特征点，每个体素中箭头的方向为该体素Fisher信息量最大的方向，把这样一种表示方式称为Fisher 信息场[25]，Fisher 信息场提供了每个体素的最优观测方向，为弱纹理环境下定位失败时相机的偏转提供了基础。

4 云台控制

4.1 偏转角度计算

为了简化实验，假设相机只能绕着y轴（垂直于地面的轴）转动。将三维空间分为M个体素，每个体素中心点在世界坐标系下的坐标为ti，垂直相机y轴平面上的Fisher 信息量最大的方向为R_best(ti)，i=1,2,…,M。当相机在空间中某一位姿（具有旋转量Rwc和平移量twc=[x,y,z]T）遇到弱纹理区域而定位失败，先找到距离当前位置欧式距离最近的体素t*，然后再以该体素Fisher信息量最大的方向作为此刻相机的最优观测方向

通过上式解出旋转矩阵R(θ)后，再转化为欧拉角θ，即待求的偏转角度。

4.2 控制规律设计

本文选择经典的PID控制器控制云台相机运动，调整相应的控制参数后，可使得云台相机无超调地快速运动到期望位置，控制律如下：

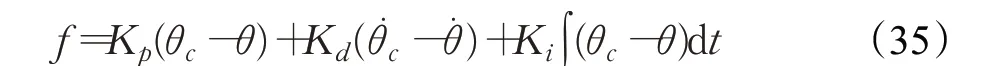
其中f为作用于云台的控制力矩，θc为云台的期望角度，θ为云台的实际角度，Kp，Kd，Ki为控制参数，具体选取的数值如表1所示。

表1 控制参数的取值Table 1 Value of control parameters

5 实验分析

5.1 仿真模型与场景

Gazebo 作为一个功能强大的物理仿真平台，具备高保真的三维物理引擎，广泛应用于机器人、无人机等设备的开发，所以本文的所有实验均是在Gazebo 平台上实现的。

在仿真环境中，四旋翼无人机和云台相机的物理模型参数如表2和表3所示。

表2 四旋翼无人机模型参数Table 2 Model parameters of quadrotor UAV

表3 云台相机模型参数Table 3 Model parameters of tilt camera

云台相机模型通过一个转动关节和四旋翼无人机模型相连，可绕着垂直地面的轴转动，如图3所示，利用4.2节设置的PID控制器可以操控相机转动到期望角度。

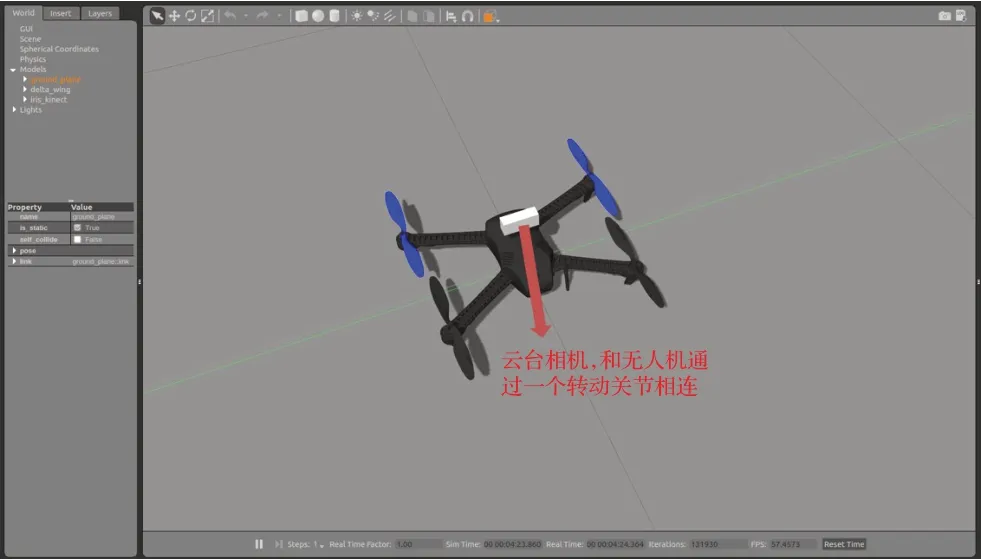
图3 仿真模型Fig.3 Simulation model

仿真场景是一个12 m×8 m×3 m 的室内环境，其中有一面无纹理的墙面，如图4所示。

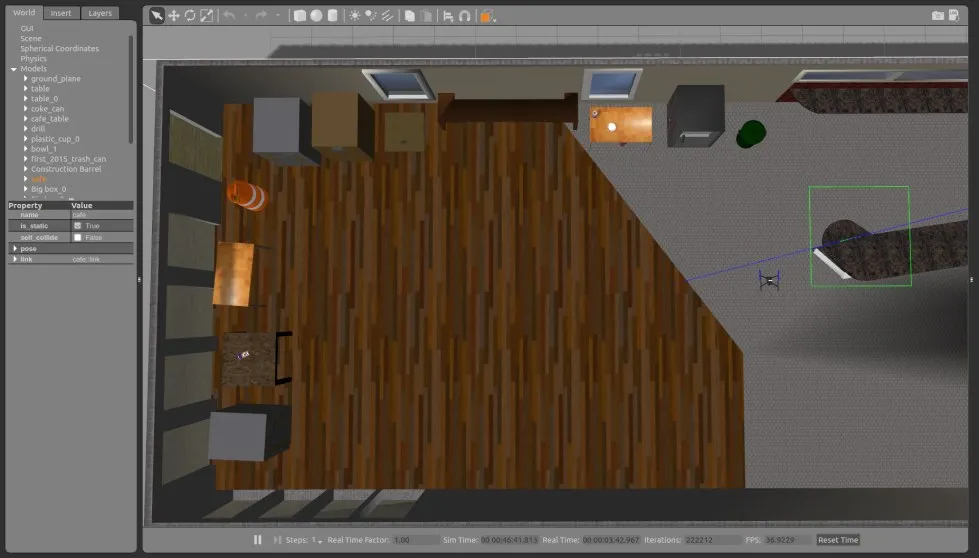
图4 室内仿真场景Fig.4 Indoor simulation scene

5.2 仿真结果与分析

无人机按照事先设定好的轨迹，先垂直飞到距离地面2 m的空中，然后沿着一个8 m×2 m的矩形绕室内飞行一周，首先用传统的ORB-SLAM2算法对无人机的位姿进行估计，得到的实验结果如图5所示。

图5（a）截取了算法前端跟踪特征点的图像，绿色的点代表匹配的特征点。从图中可以看出，当相机运动到弱纹理的墙面时，算法由于缺少特征而跟踪失败，对应的定位效果如图5（b）所示，该图表示位姿估计过程中的地图构建，包括特征点地图和关键帧地图，关键帧之间的连线表示它们的共视关系，由图可知，算法在弱纹理区域无法定位。为解决此问题，需要将空间离散化，经过测试，本文实验中的T大概为610 ms，Nf大概为30 个，t为0.007 5 ms，利用公式（31）可得体素个数Nv≤2 711，若选择2 711个体素，根据室内空间的大小，可得到体素的边长为0.474 m，为了简便运算，设置体素的边长为0.5 m，一共得到2 304 个体素，用本文所提出的主动SLAM算法，在相同环境下的运行效果如图6所示。

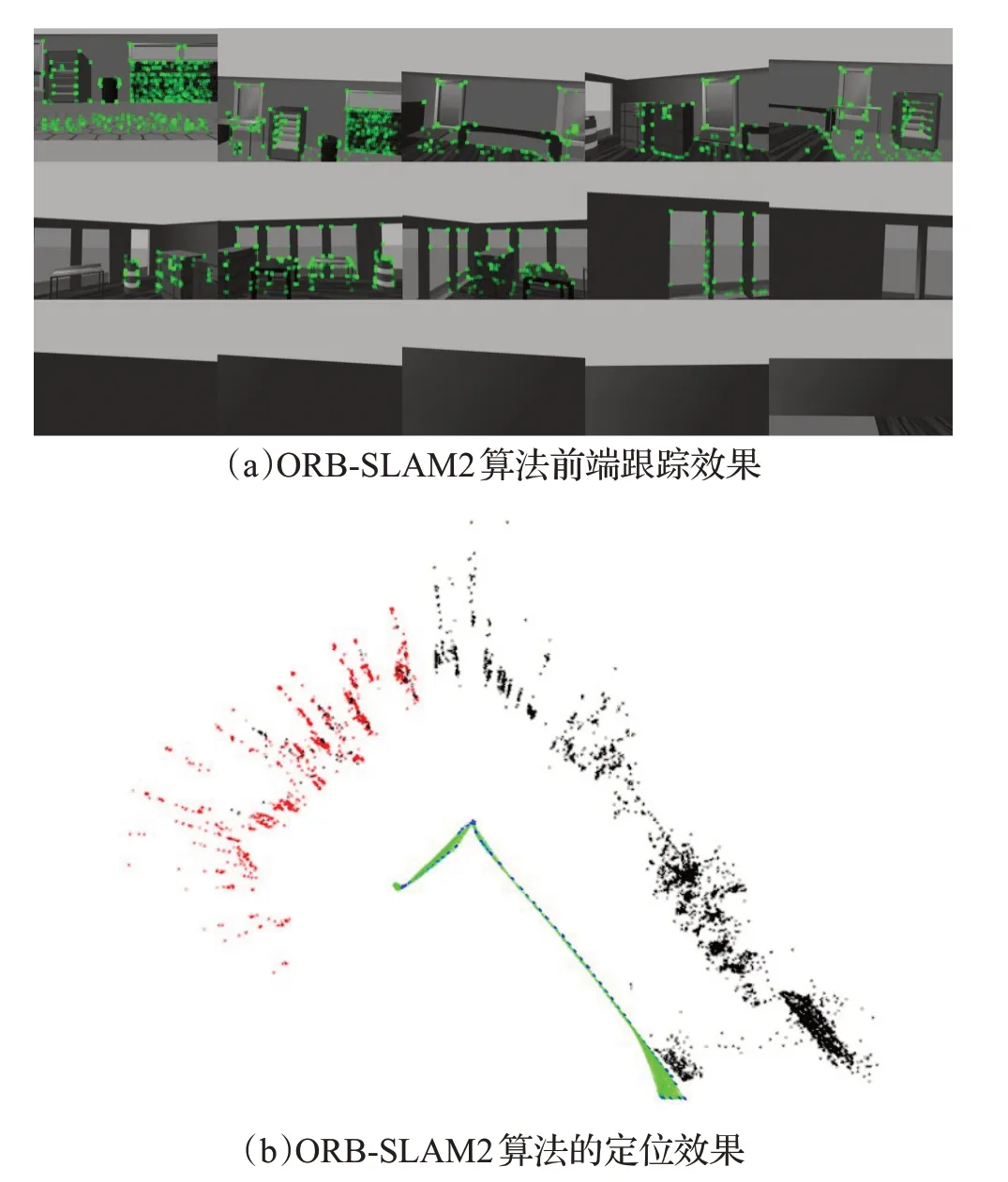
图5 ORB-SLAM2算法实验效果Fig.5 Experimental results of ORB-SLAM2

图6 主动SLAM算法实验效果Fig.6 Experimental results of active SLAM

分析图6可知，本文所提的算法在特征丢失的情况下可以完成自主重定位，进一步比较两种算法在空间中3个方向上的位置与航向角的误差（无人机在飞行的过程中俯仰和滚转角始终保持为零，不做控制），在飞行的过程中均匀地采样200 个数据，真值由仿真环境提供，结果如图7～10所示。

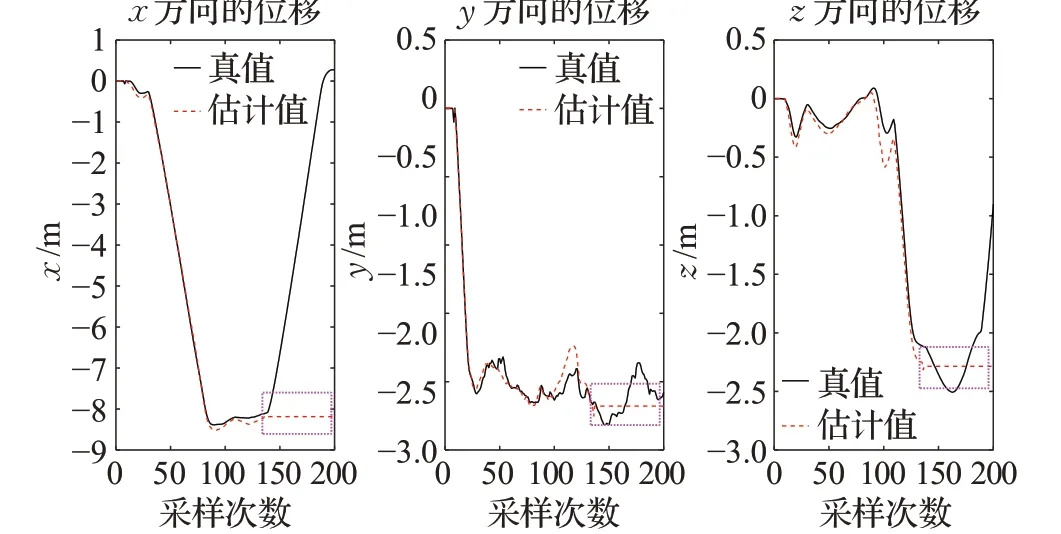
图7 ORB-SLAM2算法位置估计结果Fig.7 Results of location estimation with ORB-SLAM2

分析图7 和图9 可知，ORB-SLAM2 算法在弱纹理区域定位失败（表现为图中虚线框部分，跟踪失败后的位姿一直是失败前一时刻的位姿）；由图8和图10可知，所提算法在弱纹理区域可以通过相机的偏转进行特征捕捉，完成整个定位过程，注意到相机在偏转之后，无人机与相机的相对位移仍然保持不变，可用相机的空间位置代替无人机的空间位置，但二者之间的相对角度发生了变化，需要在航向上做一个坐标变换；如图10 所示，在第137个采样点的时候，相机转动了115.2°，因此需要在相机角度的基础上减去一个115.2°的补偿作为无人机的偏航（云台的响应时间可忽略）。表4 统计了改进前与改进后的算法在3 个方向上的位置和航向角的RMSE（均方根误差）。实验结果表明，在纹理丰富的区域，两个算法的定位效果差异不大，然而在传统ORBSLAM2 算法遇到弱纹理区域而失效的情况下，改进后的算法仍能够有效地完成位姿估计，且3个方向的位置误差都在10 cm 以内，航向定位精度在4°以内，证明了所提算法的有效性。

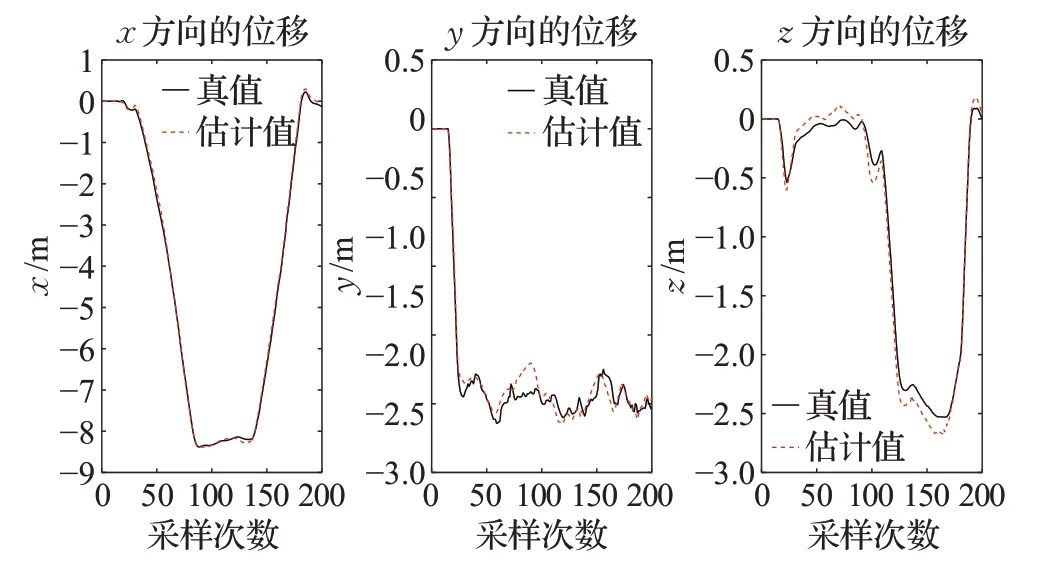
图8 主动SLAM算法位置估计结果Fig.8 Results of location estimation with active SLAM

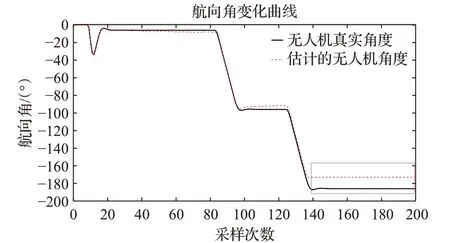
图9 ORB-SLAM2算法角度估计结果Fig.9 Results of angle estimation with ORB-SLAM2

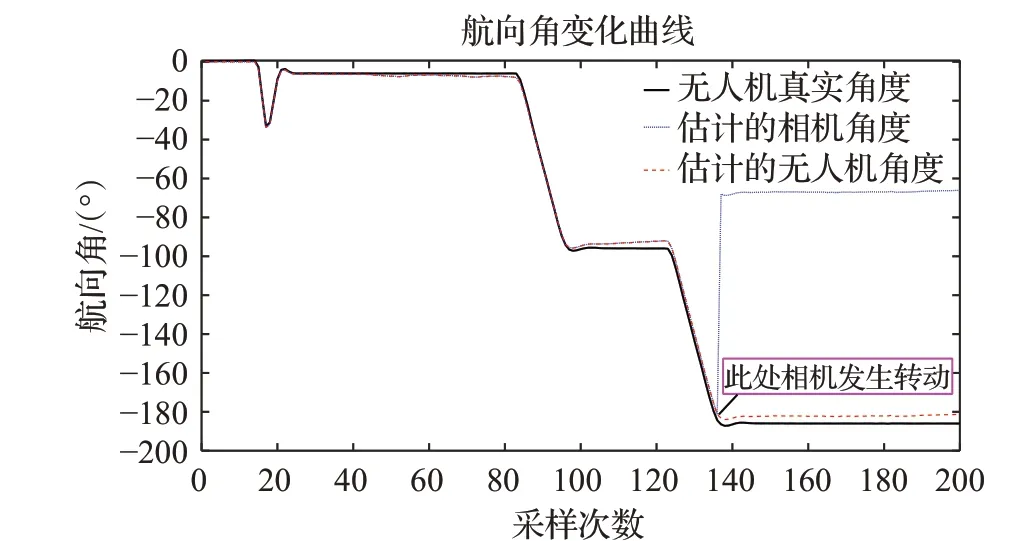
图10 主动SLAM算法角度估计结果Fig.10 Results of angle estimation with active SLAM

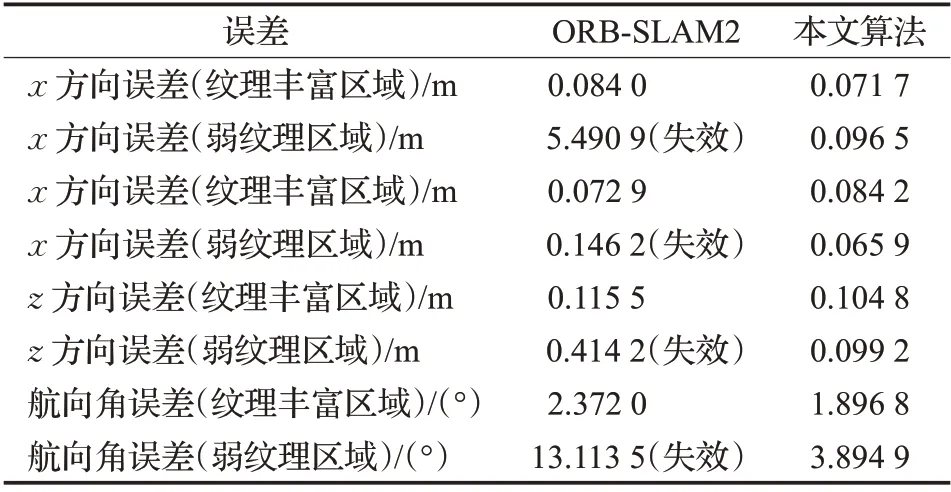
表4 均方根误差分析Table 4 Analysis of RMSE

6 结束语

本文研究了视觉SLAM 在弱纹理区域定位失败的问题，以ORB-SLAM2 框架为基础，增加了Fisher 信息场构建模块和云台控制模块，将室内的三维空间划分成若干个大小相同的体素，在定位的同时构建Fisher信息场，在特征缺失之后可以根据当前体素Fisher信息量最大的方向，计算出相机的偏转角度，然后控制相机运动到最优的观测方向进行主动重定位，提高了系统的鲁棒性，并在仿真中验证了算法的有效性。由于本文在构建Fisher信息场时并未考虑到障碍物的遮挡对特征点可观测性的影响，所以下一步将考虑用深度相机对遮挡物进行建模，在计算空间中每个体素的Fisher信息时排除某些可能被遮挡的特征点，以达到更加精准的定位效果。